矢量的运算法则ppt

矢量的加减运算法则
摘要：
一、矢量加减法简介
1.矢量加减法的基本概念
2.矢量加减法在物理中的应用
二、矢量加法法则
1.平行四边形法则
2.三角形法则
3.叉乘法
三、矢量减法法则
1.矢量减法的定义
2.矢量减法的几何意义
四、矢量加减法的应用实例
1.力的合成与分解
2.运动轨迹的计算
3.速度与加速度的计算
正文：
矢量加减法是物理学中矢量运算的基本方法，它涉及到矢量加法和矢量减法两个方面。

矢量加减法广泛应用于物理学的各个领域，如力学、电磁学等。

矢量加法是指将两个矢量相加得到一个新的矢量的过程。

矢量加法有三种基本法则：平行四边形法则、三角形法则和叉乘法。

其中，平行四边形法则是
矢量加法的基本法则，它是指将两个矢量的起点连接起来，形成一个平行四边形，新矢量的长度和方向分别等于平行四边形的对角线长度和方向。

三角形法则是将两个矢量的起点连接起来，形成一个三角形，新矢量的大小和方向分别等于三角形的第三边长度和方向。

叉乘法是将两个矢量进行向量积运算，得到一个垂直于原来两个矢量所在平面的新的矢量。

矢量减法是指将一个矢量从另一个矢量中减去得到一个新的矢量的过程。

矢量减法的定义是：将减法中的被减矢量取相反数，然后与减矢量相加。

矢量减法的几何意义是将减矢量沿着被减矢量的方向平移，使得两者相接。

矢量加减法在物理学的应用非常广泛。

例如，力的合成与分解中，我们可以通过矢量加法将多个力的矢量相加得到总力，也可以将总力分解为多个分力的矢量之和。

在运动轨迹的计算中，我们可以通过矢量加法计算物体在某一时间段内的位移和速度。

矢量点乘矢量
矢量是一种既有大小又有方向的量，又称为向量。

矢量点乘和叉乘运算法则：点乘，也叫向量的内积、数量积。

运算法则为向量a乘向量
b=allbcos。

叉乘，也叫向量的外积、向量积。

运算法则为向量c=向量a 乘向量b=absin。

1、点乘，也叫向量的内积、数量积。

顾名思义，求下来的结果是一个数。

向量a乘向量b=abcos。

在物理学中，已知力与位移求功，实际上就是求向量F与向量s的内积，即要用点乘。

2、叉乘，也叫向量的外积、向量积。

顾名思义，求下来的结果是一个向量，记这个向量为c。

向量c=向量a乘向量b=absin，向量c的方向与ab所在的平面垂直，且方向要用“右手法则”判断用右手的四指先表示向量a的方向，然后手指朝着手心的方向摆动到向量b的方向，大拇指所指的方向就是向量c的方向。

因此向量的外积不遵守乘法交换率，因为向量a乘向量b=向量b乘向量a在物理学中，已知力与力臂求力矩，就是向量的外积，良即叉乘。

第1章电磁学的数学基础——矢量分析一、矢量的定义和表示二、矢量的基本运算法则三、矢量微分元：线元，面元，体元四、标量场的梯度五、矢量场的散度六、矢量场的旋度一、矢量的定义和表示1.标量：只有大小，没有方向的物理量。

如：温度T、长度L 等2.矢量：不仅有大小，而且有方向的物理量。

如：重力、电场强度、磁场强度等G E H矢量表示为：一个矢量可以表示成矢量的模与单位矢量的乘积。

其中：为矢量的模，表示该矢量的大小。

为单位矢量，表示矢量的方向，其大小为1。

||Aˆaˆ||A A a3. 矢量表示例1：在直角坐标系中，x 方向的大小为6 的矢量如何表示？图示法：GNF fF ˆ6x axy例2：力的图示法：ˆ||A A a=ˆ6x a =矢量的图示方法1、矢量的加法运算法则加法:矢量加法是矢量的几何和,服从平行四边形规则。

a.满足交换律：A B B A+=+b.满足结合律：C A B=+BAC⇒BAC()()()()A B C D A C B D +++=+++二、矢量的基本运算法则zoyx AxA yA zA 三个方向的单位矢量表示：ˆˆˆ,,x y z aa a 根据矢量加法运算：x y zA A A A =++在直角坐标系下的矢量表示:ˆx x x A A a =其中：ˆy y y A A a=ˆz z z A A a=矢量表示为：ˆˆˆx x y y z z A A aA a A a =++矢量：ˆˆˆx x y y z z A A aA a A a =++⇩模的计算：222||xyzA A A A=++⇩单位矢量：ˆˆˆˆ||||||||y x z x y z A A A Aa a a a A A A A ==++⇩方向角与方向余弦：γβα,,||cos ,||cos ,||cos A A A A A A z y x===γβαˆˆˆcos cos cos x y z aa a αβγ=++αβγzoyxAxA yA zA 在直角坐标系下的矢量表示:矢量加法运算：ˆˆˆ()()()x x x x y y y y z z z z A B C A B C aA B C a A B C a ++=++++++++zoyxA在直角坐标系下的矢量的加法运算:BCˆˆˆx x y y z z A A aA a A a =++ˆˆˆx x y y z zB B aB a B a =++ˆˆˆx x y y z zC C aC a C a =++减法：换成加法运算()D A B A B =-=+-A B C ++BAB-逆矢量：和的模相等，方向相反，互为逆矢量。

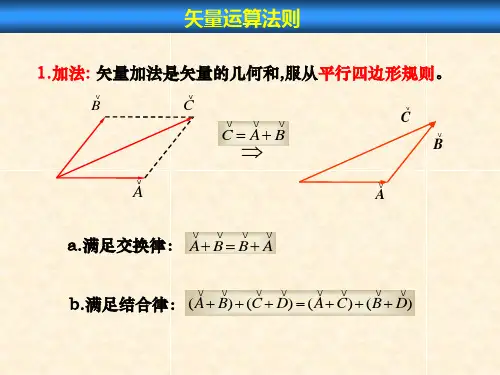
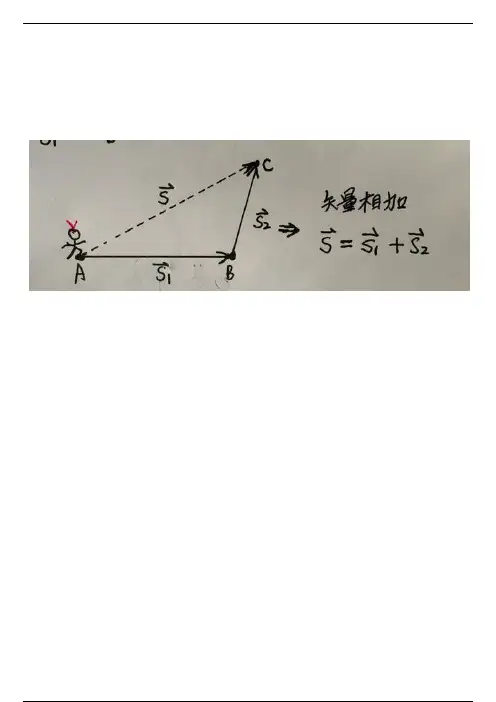
位移，速度，加速度，力等都是矢量，矢量的运算可不是简单的代数加减，而是满足三角形法则。

如图所示，某同学从A地到B地的位移为S1，从B地到C地的位移为S2，则总位移S--即前两段位移的和为从A指向C的有向线段AC---矢量相加的三角形法则。

若已知总位移S和第一段的位移S1,则第二段位移S2--即总位移与第一段位移S2的差为由B指向C的有向线段BC --矢量相减的三角形法则。

(减量指向被减量) 典型应用1.
解答：将力矢量F3平移至F4-F1，先将力矢量F3和F4相加，则和矢量恰为F1.如下图所示。

同理可知，力矢量F2和F5相加，则和矢量 也恰为F1.
所以这5个力的和矢量为3F,大小为30牛。

典型应用2.
如图所示，物体以速率v做匀速圆周运动，经时间t由A点运动到B点，AB之间恰为1/4圆弧。

物体在这段时间内的平均加速度多大？
解答：如下图所示，将物体在A点的速度矢量平移至B点，根据矢量相减的三角形定则可确定这段时间内的速度变化量，再根据加速的定义式可确定这段时间内的平均加速度大小。

看来，物体的速率不变时，物体仍可能具有加速度！。

1.2矢量的乘法运算1. 标量与矢量的乘积2. 矢量与矢量乘积(1) 标量积（点积）(2) 矢量积（叉积）3. 矢量三重积1. 标量与矢量的乘积0ˆ||00k kA k A ak k >⎧⎫⎪⎪==⎨⎬⎪⎪<⎩⎭方向不变，大小为|k |倍方向相反，大小为|k |倍A(0)kA k >(0)kA k <图示：计算：ˆˆˆx x y y z zkA kA a kA a kA a =++2. 矢量与矢量乘积(1) 标量积（点积）：||||cos A B A B θ⋅=⋅θBA两矢量的点积含义：一矢量在另一矢量方向上的投影与另一矢量模的乘积，其结果是一标量。

推论1：满足交换律推论2：满足分配律推论3：当两个非零矢量点积为零,则这两个矢量必正交。

A B B A⋅=⋅()A B C A B A C⋅+=⋅+⋅•在直角坐标系中，已知三个坐标轴是相互正交的，即ˆˆˆˆˆˆ1,1,1ˆˆˆˆˆˆ0,0,0x x y y z z x y x z y z aa aa aa aa aa aa ⋅=⋅=⋅=⋅=⋅=⋅=有两矢量点积：ˆˆˆˆˆˆ()()x x y y z z x x y y z z A B A aA a A aB a B a B a ⋅=++⋅++zz y y x x B A B A B A ++=•结论: 两矢量点积等于对应分量的乘积之和。

(2) 矢量积（叉积）：ˆ||||sin n A B A B aθ⨯=⋅BAˆn aθ含义：两矢量叉积，结果得一新矢量，其大小为这两个矢量组成的平行四边形的面积，方向为该面的法线方向，且三者符合右手螺旋法则。

推论1：不服从交换律,A B B A A B B A⨯≠⨯⨯=-⨯()A B C A B A C⨯+=⨯+⨯推论2：服从分配律推论3：不服从结合律()()A B C A B C⨯⨯≠⨯⨯推论4：当两个非零矢量叉积为零，则这两个矢量必平行。

在直角坐标系中，两矢量的叉积运算如下：ˆˆˆx y z xy z x y zaa a A B A A A B B B ⨯=ˆˆˆˆˆˆ()()x x y y z z x x y y z z A B A aA a A aB a B a B a ⨯=++⨯++ˆˆˆ()()()y z z y x z x x z y x y y x z A B A B aA B A B a A B A B a =-+-+-两矢量的叉积又可表示为：xyz o例21234ˆˆˆˆˆˆ2,32ˆˆˆˆˆˆ23,325x y z x y z x y z x y z r aa a r a a a r aa a r a a a =-+=+-=-+-=++求：4123r ar br cr =++中的标量a 、b 、c 。

§2 矢量的加减法一 矢量的加法：定义1 设a OA =、b OB =，以OA 与OB 为边作一平行四边形OACB ，取对角线矢量OC ，记c OC =，如图1-3，称 c 为 a 与b 之和，并记作c a b =+这种用平行四边形的对角线矢量来规定两个矢量之和的方法称作矢量加法的平行四边形法则.如果矢量a OA =与矢量b OB =在同一直线上，那么，规定它们的和是这样一个矢量： 若OA 与OB 的指向相同时，和向量的方向与原来两矢量相同，其模等于两矢量的模之和（图1-4）.oB ooC若OA 与OB 的指向相反时，和矢量的模等于两矢量的模之差，其方向与模值大的矢量方向一致（图1-5）.o BoC由于平行四边形的对边平行且相等，可以这样来作出两矢量的和矢量： 定义2 作OAa =，以OA 的终点为起点作ACb =，联接OC （图1-6）得a bOC c +==. （1.2-1）该方法称作矢量加法的三角形法则.(图1.1)(图1.2)(图1.3) (图1.4)矢量加法的三角形法则的实质是：将两矢量的首尾相联，则一矢量的首与另一矢量的尾的连线就是两矢量的和矢量. 据矢量的加法的定义，可以证明矢量加法具有下列运算规律： 定理 矢量的加法满足下面的运算律：1、交换律 a b b a +=+, （1.2-2）2、结合律 ()()a b c a b c a b c ++=++=++. （1.2-3） 证 交换律的证明从矢量的加法定义即可得证，结合律的证明从图1-7可得证.二 矢量的减法定义3 若c a b =+，则我们把b 叫做c 与a 的差，记为b c a =-显然， ()a b a b -=+-, 特别地， ()0a a a a -=+-=.由三角形法则可看出：要从a 减去b ，只要把与b 长度相同而方向相反的矢量b -加到矢量a 上去.由平行四边形法则，可如下作出矢量ab -（图1-8）.例1 设互不共线的三矢量a 、b 与c ，试证明顺次将它们的终点与始点相连而成一个三角形的充要条件是它们的和是零矢量.证 必要性 设三矢量a 、b 、c 可以构成三角形ABC （图1-9），即有,,AB a BC b CA c ===，那么， 0,AB BC CA AA ++== 即 0a b c ++=.(图1.5)(图1.6) ABCabc(图1.8)充分性 设0a b c ++=，作,,AB a BC b ==那么AC a b =+，所以0AC c +=，从而c CA =，所以a 、b 、c 可以构成三角形ABC .例2 用矢量法证明：对角线互相平分的四边形是平行四边形.证 设四边形ABCD 的对角线AC 、BD 交于O 点且互相平分（图1-10）因此从图可看出：AB AO OB OB AO DO OC DC =+=+=+=，所以，AB ∥DC ，且AB DC=，即四边形ABCD 为平行四边形.(图1.9)。