当前位置：文档之家 › 18讲 平面应力状态分析——图解法

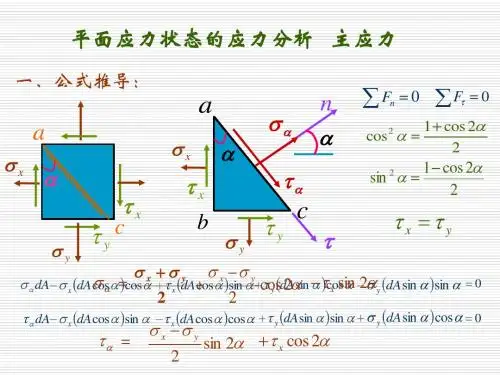
18讲 平面应力状态分析——图解法

  • 格式：pptx
  • 大小：688.77 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

6-2 平面应力状态分析

6-2 平面应力状态分析

§6-2 平面应力状态分析
xy yx
1 cos 2 x y x y cos 2 cos 2 xy sin 2 2 2 2 1 cos 2 x y sin 2 cos 2 2 sin xy 2 2 2sin cos sin 2 x y x y
cos 2 xy sin 2 90o 2 2 x y sin 2 xy cos 2 90o 2
90o x y 90o
1）相互垂直的任意两截面上的正应力之和是一个定值； 2）说明切应力互等定理的正确性。
§6-2 平面应力状态分析
二、应力圆、主应力与主平面
1、应力圆
x y x y cos 2 xy sin 2 2 2
( ) cos 2 xy sin 2 2 2 x y sin 2 xy cos 2 2
§6-2 平面应力状态分析
4、在应力圆上标出主应力和主平面方位以及最大切应力
x y 2 2 1 max x y ( ) xy min 2 2 3
2 xy
0 0 2
tan 2 0
§6-2 平面应力状态分析
解： 1）画出应力圆
60 (40) 2 30 30 2 R ( ) ( ) 58.31MPa 2 2
(
x y
2
, 0) (10, 0)
§6-2 平面应力状态分析
2）求主应力和主平面
1 68.3MPa
3 48.3MPa

7.1-7.2平面应力状态

7.1-7.2平面应力状态

y
d
x y cos sin xy cos 2 sin 2
1 cos 2 1 cos 2 利用： 2 1 sin 2 1 cos 2 2 1 sin cos sin 2 2
yx
c
x xy
75MPa 40MPa
0 1 19.33 0 2 70.67 0
0
MPa 0 1 25 0 2
?
主应力大小为：
1 39MPa
2 0 3 89MPa
?
主平面和主应力的对应问题？

x y
2 x y

x y
025MPa 0
min
max

x y
2
x y 2 xy 2
2
min
25 75 25 75 2 40 2 2
2
max 39MPa
min 89MPa
主平面位置:
2
cos 2 xy sin 2

2
sin 2 xy cos 2
x y d 2 sin 2 xy cos 2 2 d 2
由定义： 主平面：切应力等于零的截面
主应力：主平面上的正应力 结论：主应力是正应力的极值。 主平面位置:
最大切应力表达式
max 1 / 2( 1 - 3 )
确定单元体的主应力和主平面位置并 例题： 在单元体中绘出 75MPa 解： x 25MPa
y 75MPa
40MPa
xy 40MPa
025MPa 0

第十三章平面应力状态分析

第十三章平面应力状态分析

3. 连接DD’交σ轴于点C；
O
C
D'( y , yx )
4. 以点C为圆心，CD为半径作圆。

莫尔应力圆的应用
x
x'y'
b
B 应A用过程中，应当将应力圆
x'45º作x 为思考、分d 析问题c 的2×工45具º ， x'
y
o
a
D y' 而不是计算工具。 2×45º
E e
x
莫尔应力圆的应用

x
x ( ) 0 xy
α σnτα αα该 应力xxxdy圆A2 方y程2最早(由2德y((s国iyn12xx工cso程idnsA师x)ddOcAAott))osyssM2iinnoh4r（x1y8235- 2
横截任面意上一正点应处各力个分方析向和截切面应上力应力分的析集的合结，果表 明称：为同一一点处面的上应不力同状点态。的应力各不相同，此即 应力的点的概念。
x'y' x'
x'y' x'
xy
x
yx
微元平衡分析结果表明：即使同一点不
同方向面上的应力也是各不相同的，此即
应力的面的概念。
13.2应力张量
对于杆件的内力，可以用截面法求得。下面
en表示讨法论物向体单的位任矢一量个。点et表及示其截邻面域内的的受一力个状单态位。切矢量
M
τn
⊿A σn
, n en
nn 分别称为截面上正应力（法
向力）和切应力（剪切力），
p(n)
各自代表应力矢量在截面法向
n和在截面内的分量。
et
p称为点M的应力，或全应力。

材料学 平面应力状态分析

材料学 平面应力状态分析
α
ayx
f
y
t
e
dA
dAcos α
a dAsinf
3.任意斜截面上的应力(The stress acting on any inclined plane)
设斜截面的面积为dA , a-e的面积为dAcos, a-f 的面积为 dAsin
对研究对象列 n和 t 方向的平衡方程得
化简以上两个平衡方程最后得
的方位.
m
m a
l
A
解： 把从A点处截取的单元体放大如图
A
1 3
因为 x < y ，所以 0= 27.5°与min对应
3
0
A
x
1
例题5 图示单元体,已知 x =-40MPa,y =60MPa,xy=-50MPa.试求e-f截面上的应力情
况及主应力和主单元体的方位.
解:（1）求 e-f 截面上的应力
不难看出 即两相互垂直面上的正应力之和保持一个常数
二、最大正应力及方位 （Maximum normal stress and it’s direction）
1.最大正应力的方位（The direction of maximum normal stress ） 令
0 和 0+90°确定两个互相垂直的平面,一个是最大正应力
y n
e
x
a
yx
x xy
f
e
x
x
xy
α
α n
α
α
ayx
f
y
e
x
a
y
yx x
xy
f
n
x
2.符号的确定（Sign convention）
e

材料力学第18讲 Chapter7-2第七章 应力状态(应力圆)

材料力学第18讲 Chapter7-2第七章 应力状态(应力圆)

x
y
2
R cos[180o
(2
20 )]
xy
x
2
y
R cos(2
20 )
O
xy
x
y
2
R(cos 2
cos 20
sin 2
sin 20 )
x
y
2
x
2
y
cos 2
xy
sin
2
D
A ( x , xy )
y R 2 20
E
C
x
B ( y , xy )
13
单元体与应力圆的对应关系
y y
y
10
a
64103 110103 3.206107 1012
219.6MPa
200
b
64103 100103 3.206107 1012
199.6MPa
10
c
64103 0 3.206107 1012
0.0MPa
120
10
c z
b a y
30
(Fs 160kN; M 64kN m)
xy
（3）以C 为圆心，AC为半径画圆
—应力圆或莫尔圆
O
xy
y
y
xy x
Ox
A ( x , xy )
y C
B ( y , xy )
x
10
3、单元体公式与应力圆的关系
以上由单元体公式
应力圆（原变换）
下面寻求由应力圆
单元体公式（逆变换）
只有这样，应力圆才能与公式等价 换句话，单元体与应力圆是否有一一对应关系？
x
x
x
0
y 1

平面应力状态.

平面应力状态.

§7-4 平面应力状态一、一点处的应力状态及单元体在讨论轴向拉（压）杆斜截面上的应力时，我们已经知道通过拉（压）杆内任一点处的斜截面上的应力是随着截面方位角α的变化而变化的。

在圆轴扭转时，截面上各点处剪应力的大小与该点与截面形心的距离成正比例关系；等直梁弯曲时，梁横截面上各点处的正应力σ及剪应力τ随与截面中性轴的距离而变化。

因此，为了解决构件的强度问题，就要知道受荷载作用后的构件，在哪一点处及过该点处的哪个方位的斜截面上的应力是最大的，并研究其破坏的原因。

过杆件内一点的所有不同方位截面上在该点处的应力情况，称为此点处的应力状态。

如图7-18a 所示，为研究梁在荷载作用下其横截面m —m 上A 点处的应力情况，围绕该点取一个边长为微分量的正六面体为研究对象，这个微六面体称为单元体。

在m —m 截面处截取微段长dx ，然后在A 点处用两相距为dy 高的上下水平面和相距宽为dz 的前后竖直平面相切割，取出单元体（又称微元体）, 如图7-18b 所示。

根据梁的M 和Q 图（图7-18c ）可知，此单元体左侧截面上有受压的正应力σ和向上的切应力τ，由于梁在荷载作用下是平衡的，因而从其中取出的单元体也应平衡，则单元体右侧截面有受压的正应力σ和向下的切应力τ，根据剪应力互等定理得出上下水平面上的应力如图7-18b 所示。

当前后竖直平面上的应力为零时的应力状态，称为平面应力状态，可用如图7-18d 所示的平面图形表示。

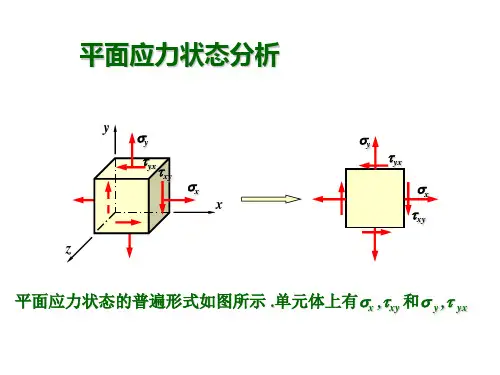
Q 图M 图a )c)dxτd )m-m 截面图7-18二、平面应力状态分析——解析法从受力构件内取出一点，其平面应力状态的单元体，如图7-19a 所示。

四个侧面上的应力为x σ、x τ和y σ、y τ。

单元体前后两个面上的应力为零，可用如图7-19b 所示的平面图形表示。

dAcosαdAxdA sinαc efαb)a)c)d)图7-19现讨论图示单元体中任意斜截面ef上的应力。

斜截面的方位角α从x截面（其法线与x 轴重合）量起，以逆时针转向为正。

材料力学课件：第7章 应力状态分析

示。
显然，用主应力表示的应力状态要比用一般 应力分量表示的应力状态简单。用主应力表 示一点处的应力状态可以说明某些应力状态 表面上是不同的，但实质是相同的，即其主 应力和主方向都相同。
纯剪切状态的最大应力
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
平面应力状态有两个不等于零主应力，这两个 不等于零的主应力以及上述平面应力状态固有的等于 零的主应力，分别用表示 :
根据主应力的大小与方向可以确定材料何时发生 失效或破坏，确定失效或破坏的形式。因此，可以说 主应力是反映应力状态本质内涵的特征量。
TSINGHUA UNIVERSITY
根据上述分析结果，原来用x、y、xy 和yx表示的应力状态，现在可以用主应力表
( x y ) sin 20 2 xy cos 20 0
2
(
σx
σy 2
) s
i
n
2α0
τx
yc
o
s
2α0
2τα0
0
即α＝α0 时，切应力为零
y
2 xy x
2 0
tan
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
1 2
(
x
y)
1 2
( x
y ) cos 2
xy
sin
2
1 2
( x
y ) sin
2
xy
cos 2
法二: 解析法
1 2
(
x
y)
1 2
(
x

19讲 平面应力状态分析图解法


y

R (
x y
2
2 ) 2xy
R
( a,0)
x
(
R
x y
2 ,0)

应力圆是个信息源(从力学观点分析） （1）若已知一个应力单元体两个互相垂直面上的 应力就一定可以作一个圆，圆周上的各点坐标值， 就是该单元体任意斜截面 上的应力。 （2）平面应力状态下任意斜截面 上的应力相互
第十八讲 平面应力状态分析——图解法
湖南理工学院——曾纪杰
一 应力圆


x y
2

x
y
2
x
cos 2 sin 2 x
y
(

x y
2
)

x y
2
2
(1) cos 2 sin 2 x (2)
sin 2 2 xcos



y
y
a (a ,a )

x
A
c

x

转向对应——半径旋转方向与方向面法线旋转方向一致；
二倍角对应——半径转过的角度是方向面旋转角度的两倍。



D
y
y
n

A
d
2
a

x
x
x
c


y

y
B A

x
O
c
b(y ,y)
a(x ,x)


x
二.应力圆的应用
单向拉伸
x

b
B
x'
x
xy x y

平面应力状态演示文稿


7
F
N
A
K
F
A
F
K
p A .
pF Acos0cos
p co sco 2s
psi n20si2 n
8
§8-1-1 应力状态的概念
State of the Stresses of a Given Point
1、应力状态：受力构件内任意点各截面方位上的应力
情况。
研究方法： 取单元体的方法。
2、单元体：围绕受力构件内任意点切取的微元体。
( Three-Dimensional State of Stresses )
x
x
z
z
zx zy
xz yz
xy
yx
yy
.
17
平面（二向）
应力状态
x
( Plane State of Stresses )
.
y
yx xy
x
y
18
y
x
x
y
yx xy
x
单向应力状态
( One Dimensional State of Stresses )
.
1
本章要点
（1）平面应力状态的解析法和图解法 （2）强度理论
重要概念
单元体、平面应力状态、平面应变状态、主应力、 主应变、广义虎克定律、第一强度理论、第二强度 理论、第三强度理论、第四强度理论。
.
2
目录
§8-1 应力状态的概念和实例 §8-2 平面应力状态下的应力状态分析 §8-3 三向应力状态 §8-4 变形与应变 §8-5 广义虎克定律与弹性变形比能 §8-6 强度理论的概念及应用
V 2GI P
5

《材料力学》课件7-2平面应力状态的应力分析主应力

2 0
3 110MPa
max 172.5MPa
o
c

平面应力状态的几种特殊情况

x y
2
x y
2
cos 2 x sin 2

x y
2
sin 2 x cos 2
轴向拉伸压缩
x
2 (1 cos 2 )
60 0

f
n
30 5.2MPa
0
30 0.8MPa
0
对于图中所示之平面应力状态，若要求面内最大切应力 τmax＜85MPa，试求τx的取值范围。图中应力的单位为 MPa。

50
x
50 , y
d
100
o
2
2
二、符号规定：
正应力
y
α角
由x正向逆时针转到n正 向者为正；反之为负。
拉应力为正
x
压应力为负
x
n x

x
y
切 应 力

使单元体或其局部顺 时针方向转动为正；反之 为负。
某单元体应力如图所示，其铅垂方向和水平方向各平面 上的应力已知，互相垂直的二斜面ab和bc的外法线分别与x 轴成300和－600角，试求此二斜面ab和bc上的应力。
2
x 40MPa
主应力和主平面

2
(y ,y)

2
x y 2
2
2 x
a ( x , x)
o
c
d
1
1

x y
2 x y 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

作业：孙训方，《材料力学》（第五版） 7-7 a；d
x 60MPa, xy 30MPa. y 40MPa,
试求（1）斜面上的应力；（2）主应力、主平面； （3）绘出主应力单元体a
解：用应力圆解法 3 48.3MPa
1 68.3MPa
40
a(40,30)
30MPa
60MPa
1

2
o
y
2
1 D
xy
主方向的确定 a (x ,xy)
A
x
o yx
o 2
1
d
2o
c g 1
2
tg2


x

xy x
y
2
负号表示从主应力的正方向
到x轴的正方向为顺时转向
面内最大剪应力
对应应力圆上的 最高点的面上切应力 最大，称为“ 面内 最大切应力”。
半径为R的圆，则
(
x
y )2 2


2
( x
y )2 2


2是个应力圆的方程
x
y

R
( x

y )2


2 xy
2
R
x
(a,0)
R

( x y ,0) 2
应力圆是个信息源(从力学观点分析）
（1）若已知一个应力单元体两个互相垂直面上的应 力就一定可以作一个圆，圆周上的各点坐标值，就

y
y
n
x
E
x
E( , )
(
x,
)
x
2

(
y,
)
y
点面相对应，首先找基准。 转向要相同，夹角两倍整。
平面应力状态下主平面、主应力及主方向
y
x
D
x
A
y

o B1 d
a
20
c
A1
主平面：τ = 0, 与应力圆上和横轴交点对应的面
平面应力状态下主平面、主应力及主方向
第十八讲 平面应力状态分析——图解法
湖南理工学院——曾纪杰
一.应力圆


x
y
2
x
y cos 2
2
x sin 2
(
x
y)
2
x
y cos 2
2
x sin 2
(1)


x
y sin 2
2
x cos 2
是该单元体任意斜截面 上的应力。 （2）平面应力状态下任意斜截面 上的应力相互
制约在圆周上变化。
应力圆的画法
y
y
D
x
A

x (y ,y)d
( x
y )2


2 x
2
R
a (x ,x)
c

x y
2
在σ-τ坐标系中，标定与微元A、D面上 应
力对应的点a和d 连ad交 σ轴于c点，c即为圆心，cd为应
e
(10,0)
f
o c 2o

60
tg2 p

2 xy x y

0.6
p 15.48
b(60,30)
d (9.02,58.3)
R (60 (40))2 ( 30 30)2 58.31MPa
2
2
主应力单元体：
3
o
1
1 68.3MPa, 2 0,3 48.3MPa

y
y
B
x
A
x

O
c
b(y ,y)
a(x ,x)
二.应力圆的应用
单向拉伸

x
B
A
x'45º x
d
y
o
D y'
E
x
b
2×45º

c
a
2×45º
e
纯剪切

a (0, )
D
45
B
45o＝ E e
2×45º
c o
b
A
2×45º
d (0,- )
平面应力状态下求任意截面上的应力（证明P215）
力圆半径。
几种对应关系
点面对应——应力圆上某一点的坐标值对应着 微元某一方向面上的正应力和切应力

y
a( a , a )
y
A x
c

x
转向对应——半径旋转方向与方向面法线旋转方向一 致；
二倍角对应——半径转过的角度是方向面旋转 角度的两倍。

y
y
n
x x
D
x
A
a
d 2
c
(2)
对(1) (2)式两边平方，将两式相加，并利用
sin2 2 cos2 2 1 消去 sin 2 和 cos 2，得
(
x
y )2
2


2
( x
y )2
2


2 x
(3)
比照解析几何的曲线方程 (x a)2 y2 R2 是一个圆心在(a.0),

max a
o B1 d
2o
c
A1
例题1: 试用应力圆法计算图示单元体e--f截面上的应 力。图中应力的单位为MPa。

e 2.2 4.4 300
f
n
a
c 600
o

d
300 5.2MPa 300 0.8MPa
例题2 一点处平面应力状态如图所示。已知 30,
主应力的确定
y
x
D
x
A y

o B1 d
a
2αo

c
A1
oA1
0c cA1
x y
2
(
x

y
)2

2 xy
2
oB1

0c
cB1

x
y
2

(
x


y
)2


2 xy
2
主应力排序：

o 2
d
a
2p

c 1
3


3 o