下载文档原格式
实验应力分析实验报告1. 引言应力分析是工程领域中的重要研究方向之一。
通过对材料在外力作用下的应力变化进行分析，不仅可以深入理解材料的力学性质，还可以为工程设计和结构优化提供可靠的依据。
本实验旨在通过实际操作和数据分析，研究材料在不同外力下的应力分布和变化规律。
2. 实验目的本实验的主要目的是通过应力分析实验，探究材料在外力作用下的应力分布，并通过数据采集和处理，分析不同因素对应力的影响。
3. 实验装置和材料本实验所使用的装置和材料有：•应力传感器：用于测量材料受力时的应力变化。
•外力加载器：用于施加不同大小的力。
•试样：材料样本，用于承受外力并传导到应力传感器上。
4. 实验步骤4.1 准备工作1.检查实验装置和材料的完好性，并确保其能正常工作。
2.根据实验要求选择合适的试样，并进行必要的准备工作，如清洁和测量尺寸。
4.2 搭建实验装置1.将应力传感器连接到数据采集系统，并确保连接稳定可靠。
2.将外力加载器与应力传感器相连，确保其能够传递施加的力。
4.3 实验操作1.将试样安装在外力加载器上，并调整加载器的位置，使试样受力均匀。
2.根据实验设计，逐步加载外力，并记录下相应的应力数据。
3.根据需要，可以进行多组实验，以获得更全面的数据。
4.4 数据处理和分析1.对采集到的应力数据进行整理和清洗，确保数据的准确性和可靠性。
2.利用适当的数学方法和工具，分析数据并绘制应力-应变曲线。
3.根据实验结果，分析不同因素对应力的影响，如外力大小、试样尺寸等。
4.对实验结果进行讨论，并提出可能的改进方案。
5. 实验结果与讨论根据实验操作和数据处理，我们得到了一系列的应力-应变曲线，并通过分析得出以下结论：1.随着外力的增加，材料的应力呈线性增加趋势。
2.不同尺寸的试样在相同外力下的应力略有差异，但总体趋势相似。
3.应力分布在材料中的变化不均匀，存在一定的差异性。
通过以上结果和分析，我们可以进一步深入研究材料的力学性质，为工程设计和结构优化提供可靠的参考依据。
工程力学中的应力和应变分析工程力学是应用力学原理解决工程问题的学科，它研究物体受外力作用下的力学性质。
应力和应变是工程力学中的重要概念，它们对于分析材料的强度和变形特性具有重要意义。
本文将就工程力学中的应力和应变进行详细分析。
一、应力分析应力是指物体单位面积上的内部分子间相互作用力。
根据作用平面的不同，可以分为法向应力和剪切应力两种。
1. 法向应力法向应力是指力作用垂直于物体某一截面上的应力。
根据物体受力状态的不同，可以分为拉应力和压应力两种。
- 拉应力拉应力是指作用于物体截面上的拉力与截面面积的比值。
拉应力的计算公式为：σ = F/A其中，σ表示拉应力，F表示作用力，A表示截面面积。
- 压应力压应力是指作用于物体截面上的压力与截面面积的比值。
压应力的计算公式与拉应力类似。
2. 剪切应力剪切应力是指作用在物体截面上切向方向上的力与截面面积的比值。
剪切应力的计算公式为：τ = F/A其中，τ表示剪切应力，F表示作用力，A表示截面面积。
二、应变分析应变是指物体由于外力的作用而产生的形变程度。
根据变形情况，可以分为线性弹性应变和非线性应变。
1. 线性弹性应变线性弹性应变是指物体在小应力下，应变与应力成正比，且随应力消失而恢复原状的应变现象。
线性弹性应变的计算公式为：ε = ΔL/L其中，ε表示线性弹性应变，ΔL表示物体的长度变化，L表示物体的原始长度。
2. 非线性应变非线性应变是指物体在较大应力下，应变与应力不再呈线性关系的应变现象。
非线性应变的计算公式较为复杂，需要根据具体情况进行分析。
三、应力和应变的关系应力和应变之间存在一定的关系，常用的关系模型有胡克定律和杨氏模量。
1. 胡克定律胡克定律是描述线性弹性材料的应力和应变之间关系的基本模型。
根据胡克定律，拉应力和拉应变之间的关系可以表示为：σ = Eε其中，σ表示拉应力，E表示弹性模量，ε表示拉应变。
2. 杨氏模量杨氏模量是描述材料抵抗拉伸或压缩变形能力的物理量。
工程力学中的杆件和梁的应力分析工程力学是工程学科的重要分支之一，它研究物体在受力作用下的力学性质。
在工程实践中，杆件和梁是常见的结构构件，其应力分析是工程设计和计算的基础。
本文将从杆件和梁的应力分析角度探讨工程力学中的相关知识。
一、杆件的应力分析杆件是一种细长的结构构件，承受轴向力的作用。
在杆件的静力学中，应力是一个重要参数，用于描述杆件内部受力的强度和稳定性。
杆件的应力可以分为正应力和切应力。
1. 正应力正应力是指垂直于杆件截面的作用力在该截面上的单位面积，通常用σ表示。
正应力的计算可以使用公式：σ = F / A其中，F为作用力的大小，A为截面积。
正应力可以分为拉应力和压应力两种情况。
当作用力沿着杆件的轴向，方向与截面的法线方向一致时，称为拉应力。
拉应力是正值，表示杆件受拉的状态。
当作用力沿着杆件的轴向，方向与截面的法线方向相反时，称为压应力。
压应力是负值，表示杆件受压的状态。
2. 切应力切应力是指杆件截面上作用力的切向力与该截面上的单位面积之比，通常用τ表示。
切应力的计算可以使用公式：τ = F / A其中，F为作用力的大小，A为截面积。
切应力主要存在于杆件的连接部分，例如螺纹连接、焊接连接等。
切应力会引起杆件的剪切变形和破坏，需要在设计过程中加以考虑。
二、梁的应力分析梁是一种用于承受弯曲力的结构构件，具有横截面的特点。
在梁的应力分析中，主要考虑的是弯矩和截面弯曲应力。
1. 弯矩弯矩是指作用在梁上的力对其产生的弯曲效应。
在工程实践中，梁通常是直线形状，因此弯矩在横截面上呈现出分布的特点。
弯矩可以通过力学平衡和弹性力学原理进行计算。
弯矩的大小与力的大小和作用点的位置有关，计算公式为：M = F * d其中，M为弯矩，F为作用力的大小，d为作用点到梁的某一端的距离。
2. 截面弯曲应力截面弯曲应力是指由于弯曲效应，在梁的横截面上产生的应力。
截面弯曲应力的大小与弯矩和横截面的几何形状有关，计算可以使用弯曲应力公式进行。
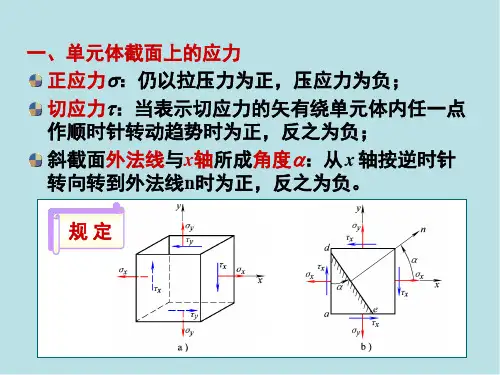
8 应力状态与应变状态分析1、应力状态的概念，2、平面应力状态下的应力分析，3、主平面是切应力为零的平面，主应力是作用于主平面上的正应力。
（1）过一点总存在三对相互垂直的主平面，对应三个主应力,主应力排列规定按代数值由大到小为:321σσσ≥≥最大切应力为132max σστ-=（2）任斜截面上的应力ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=（3) 主应力的大小22minmax )2(2xyyx yx τσσσσσ+-±+=主平面的方位yx xytg σστα--=2204、主应变122122x y x y xy xyx y()()tg εεεεεεγγϕεε⎡=+±-+⎣=-5、广义胡克定律)]([1z y x x E σσμσε+-=)]([1xzyy Eσσμσε+-=)]([1yxzz Eσσμσε+-=Gzxzxτγ=Gyzyzτγ=，Gxyxyτγ=6、应力圆与单元体之间的对应关系可总结为“点面对应、转向相同、夹角两倍。
”8.1试画出下图8.1(a)所示简支梁A点处的原始单元体。
图8.1[解]（1）原始单元体要求其六个截面上的应力应已知或可利用公式直接计算，因此应选取如下三对平面：A点左右侧的横截面，此对截面上的应力可直接计算得到；与梁xy平面平行的一对平面，其中靠前的平面是自由表面，所以该对平面应力均为零。
再取A点偏上和偏下的一对与xz平行的平面。
截取出的单元体如图8.1(d)所示。
(2)分析单元体各面上的应力:A点偏右横截面的正应力和切应力如图8.1(b)、(c)所示，将A点的坐标x、y代入正应力和切应力公式得A点单元体左右侧面的应力为：zMyIσ=bIQSzz*=τ由切应力互等定律知,单元体的上下面有切应力τ；前后边面为自由表面，应力为零。
在单元体各面上画上应力，得到A点单元体如图8.1(d)。
8.2图8.2(a)所示的单元体,试求（1）图示斜截面上的应力;（2）主方向和主应力，画出主单元体;（3）主切应力作用平面的位置及该平面上的正应力，并画出该单元体。
解题范例[解]（1）求斜截面上的正应力︒30－σ和切应力︒30－τ图8.2由公式MPa 5.64)60sin()60()60cos(21005021005030-=︒---︒---++-=︒-σMPa 95.34)60cos()60()60sin(21005030=︒--+︒---=︒-τ（2）求主方向及主应力8.01005012022tan -=----=--=y x x σστα ︒-=66.382α︒=︒-=67.7033.1921αα最大主应力在第一象限中，对应的角度为070.67α=︒，主应力的大小为15010050100cos(270.67)(60)sin(270.67)121.0MPa 22σ=⨯︒--⨯︒=－＋－－＋由yx σσσσαα+＝＋21可解出21(50)100(121.0)71.0MPax y ασσσσ=+=-+-=-－因有一个为零的主应力，因此)33.19(MPa0.7133︒--＝第三主方向＝ασ画出主单元体如图8.2(b)。
（3）主切应力作用面的法线方向25.1120100502tan =---='α ︒='34.512α︒='︒='67.11567.2521αα主切应力为'2'1MPa 04.96)34.51cos()60()34.51sin(210050ααττ-=-=︒-+︒--=此两截面上的正应力为MPa 0.25)34.51sin()60()34.51cos(2100502100501=︒--︒--++-='ασMPa 0.25)34.231sin()60()34.231cos(2100502100502=︒--︒--++-='ασ主切应力单元体如图8.2（c ）所示。
由yx MPa σσσσαα+==+=+''500.250.2521，可以验证上述结果的正确性。
8.3 试用图形解析法，重解例8.2。
[解] （1）画应力圆建立比例尺，画坐标轴τσ、。
对图8.2(a)所示单元体，在τσ-平面上画出代表x x τσ、的点A(-50,-60)和代表yy τσ、的点B(100,60)。
连接A 、B ，与水平轴σ交于C 点，以C 点为圆心，CB （或CA ）为半径，作应力圆如图8.3所示.图8.3(2) 斜截面上的应力在应力圆上自A 点顺时针转过︒60，到达G 点。
G 点在τσ、坐标系的坐标即为该斜截面上的应力，从应力圆上可直接用比例尺测量或计算得到G 点的水平和垂直坐标值：64.5ασ=-MPaτα=34.95MPa(3)主方向、主应力及主单元体图8.3所示应力圆图上H 点横坐标OH 为第一主应力，即1121.04MPa OH σ==K 点的横坐标OK 为第三主应力，即371.04MPa OK σ==-由应力圆图上可以看出，由B 点顺时针转过02α为第一主方向，在单元体上则为由y轴顺时针转0α，且00238.66,19.33αα=︒=︒应力圆图上由A 顺时针转到K 点(︒=∠66.38ACK )，则在单元体上由x 轴顺时针转过︒33.19为第三主方向,画出主单元体仍如图8.2(b)所示。
（4）主切应力作用面的位置及其上的应力图8.3所示应力圆上N 、P 点分别表示主切应力作用面的相对方位及其上的应力。
在应力圆上由B 到N ，逆时针转过︒34.51，单元体上max τ作用面的外法线方向为由y轴逆时针转过︒67.25，且MPa 04.96min max ==-=CB ττmin max ττ和作用面上的正应力均为25MPa,主切应力作用面的单元体仍如图8.2(c)所示。
8.4 如图8.4所示两端封闭的薄壁筒同时承受压强p 和外力矩m 的作用。
在圆筒表面a 点用应变仪测出与x 轴分别成正负45︒方向两个微小线段ab 和ac 的的应变ε45︒＝629.4×10–6，ε–45︒＝－66.9×10–6，试求压强P 和外力矩m 。
已知薄壁筒的平均直径d ＝200mm ，厚度t ＝10mm ， E ＝200GPa ，泊松比μ＝0.25。
图8.4[解] （1）a 点为平面应力状态,在a 点取出如图8.4(c)所示的原始单元体，其上应力：22,,42x y x pd pd m t t d t σστπ===-（2）求图8.4(c)斜单元体efgh 各面上的正应力：24524532283228x yx x y x pd mt d t pd m t d t σσστπσσστπ-+=-=++=+=-（3）利用胡克定律，列出应变ε45︒、ε–45︒表达式()()()()()()2454545245454511321181132118pd m E E t d t pd m E E t d t εσμσμμπεσμσμμπ---⎡⎤=-=-++⎢⎥⎣⎦⎡⎤-=-+⎢⎥⎣⎦＝-将给定数据代入上式663213200210629.4100.75 1.252001081020010p m π-⎛⎫⨯⨯⨯=⨯⨯+⨯ ⎪⨯⨯⨯⎝⎭66321320021066.9100.75 1.252001081020010p m π-⎛⎫⨯⨯-⨯=⨯⨯-⨯ ⎪⨯⨯⨯⎝⎭得压强和外力矩p ＝10MPa ， m ＝35kNm8.5矩形截面简支梁如图8.5所示，已知梁的横截面面积为A ，截面惯性矩为I ，材料的弹性模量为E ，泊松比为μ,梁外表面中性层上A 点45°方向的线应变为ε450。
请选择荷载F.图 8.5(A) A E με-︒145 （B ）A E 145-︒με (C) A E )1(4945με-︒ （D ）A E )1(9445με-︒答案:(A)8.1 单元体最大正应力面上的切应力恒等于零吗?[解] 正确。
因为在主平面上的正应力σ1是单元体各截面上正应力的极值（可以为最大值），而主平面上切应力为零。
8.2 单元体最大切应力面上的正应力恒等于零,对吗?[解] 不正确。
三向应力状态下单元体有3个主应力，而最大切应力由31σσ决定，即：231max σστ-=8.3 若一单元体中两个面上切应力数值相等 , 符号相反 , 则该两平面必定相互垂直 , 这种说法对吗?[解] 正确。
由切应力双生互等定理知,若切应力数值上21ττ=，符号相反时，该两平面必定相互垂直。
图 8.68.4 直径 d=20mm 、L=2m 的 圆截面杆,受力如图 8.7 。
试绘杆件中 A 点和 B 点的单元体受力图,算出单元体上的应力的数值,并确定这些点是否为危险点。
1τ2τ1τ2τxσσyσyσ习题解析[解] 以下图8.8为图8.7各单元体受力图：图 8.8 应力计算:图（a ）的A 点 :a N63.69MP A σ==-（c ） 图 8.7(a) （b ） （d ）点A 点A 点A )(a )(c )(b 点B )(d 点B ττστσσ点A σ图（b ）的A 点:a38050.96MP d 16τ==π 图（c ）的A 点:a N127.38MP A σ==B 点:aN127.38MP A σ== , a 38050.96MP d 16τ==π 图（d ）中A 点(压应力):3a33zM 201025.48MP 1W 3.14(2010)32-⨯σ===⨯⨯⨯ B 点:*z az QS 4Q 0.17MP I b 3A τ===(b ）中的A 为危险点，（c ）中的A 、B 为危险点，（d ）中的A ，B 点均为危险点,相比之下A 点的应力较大。
8.5 已知应力状态如图 8.9 所示(应力单位:MPa)。
试用图解法求: (1)(a)、(b)中指定斜截面上的应力;并用解析法校核之;(2) (c)、(d) 、(e)上主应力的大小与方向,在单元体上画出主平面的位置 ,求最大切应力。
(a)300斜截面单元本;(b)450斜截面单元体;(c) 纯切应力单元体;(d) 压拉切单元体 (e) 拉压切单元体。
图 8.9[解](a) 按比例画出应力圆如下图,可得α=300的斜截面的正应力和切应力为E点的坐标为30a45MP︒σ=30a8.5MP︒τ=解析法校核：x y x yx ax yx a30505030cos2sin2cos6045MP 222250303sin2cos2538.5MP222αασ+σσ-σ+-σ=+α-τα=+=σ-σ-τ=α+τα=⋅==(b)用比例画出应力圆,E点的坐标为45a5MP︒σ=45a25MP︒τ=解析法校核：x y x yx a x yx a 5050cos 2sin 2cos 9020sin 905MP 222250sin 2cos 2sin 9025MP 22αασ+σσ-σσ=+α-τα=+-=σ-στ=α+τα=⋅=(c ）应力圆如下图,与σ轴的交点即为主应力的对应点，从应力圆上可按比例直接量得两个主应力之值分别为：11a 232aOA 50MP ,0,OA 50MP σ==σ=σ==-主平面的方位可由应力圆上量得,因112D OA 90ϕ=∠=-最大主应力作用面与x 平面之夹角为(从D1到A1是顺时针转的):45ϕ=-13max a50MP 2σ-στ==最大切力；(d ）应力圆与σ轴的交点即为主应力得应点，从应力图上可按比例直接量得两个主应力之值分别为：yσCEXO τY2α11a22a3OA70MPOA30MP,0σ==σ==σ=最大主应力作用面与x平面之夹角为(可由应力圆上得):12FCA9045ϕ=∠=-ϕ=-max aCF20MPτ==最大切力(e）应力圆与σ轴的交点即为主应力的对应点，从应力圆上可按比例直接量得两个主应力之值分别为11a32aOA44.7MP OA44.7MPσ==σ==-主平面的方位，可由应力圆上量得：226.513.2ϕ=-ϕ=-（对应于主应力σ1所在主平面）max a40MPτ=最大切力8.6图 8.10 示单元体 ( 单位为 MPa), 问分别属于什么应力状态。
