一点的应力状态-经典

弹性⼒学_第⼆章__应⼒状态分析第⼆章应⼒状态分析⼀、内容介绍弹性⼒学的研究对象为三维弹性体，因此分析从微分单元体⼊⼿，本章的任务就是从静⼒学观点出发，讨论⼀点的应⼒状态，建⽴平衡微分⽅程和⾯⼒边界条件。

应⼒状态是本章讨论的⾸要问题。

由于应⼒⽮量与内⼒和作⽤截⾯⽅位均有关。

因此，⼀点各个截⾯的应⼒是不同的。

确定⼀点不同截⾯的应⼒变化规律称为应⼒状态分析。

⾸先是确定应⼒状态的描述⽅法，这包括应⼒⽮量定义，及其分解为主应⼒、切应⼒和应⼒分量；其次是任意截⾯的应⼒分量的确定—转轴公式；最后是⼀点的特殊应⼒确定，主应⼒和主平⾯、最⼤切应⼒和应⼒圆等。

应⼒状态分析表明应⼒分量为⼆阶对称张量。

本课程分析中使⽤张量符号描述物理量和基本⽅程，如果你没有学习过张量概念，请进⼊附录⼀，或者查阅参考资料。

本章的另⼀个任务是讨论弹性体内⼀点－微分单元体的平衡。

弹性体内部单元体的平衡条件为平衡微分⽅程和切应⼒互等定理；边界单元体的平衡条件为⾯⼒边界条件。

⼆、重点1、应⼒状态的定义：应⼒⽮量；正应⼒与切应⼒；应⼒分量；2、平衡微分⽅程与切应⼒互等定理；3、⾯⼒边界条件；4、应⼒分量的转轴公式；5、应⼒状态特征⽅程和应⼒不变量；知识点：体⼒；⾯⼒；应⼒⽮量；正应⼒与切应⼒；应⼒分量；应⼒⽮量与应⼒分量；平衡微分⽅程；⾯⼒边界条件；主平⾯与主应⼒；主应⼒性质；截⾯正应⼒与切应⼒；三向应⼒圆；⼋⾯体单元；偏应⼒张量不变量；切应⼒互等定理；应⼒分量转轴公式；平⾯问题的转轴公式；应⼒状态特征⽅程；应⼒不变量；最⼤切应⼒；球应⼒张量和偏应⼒张量§2.1 体⼒和⾯⼒学习思路:本节介绍弹性⼒学的基本概念——体⼒和⾯⼒，体⼒F b和⾯⼒F s的概念均不难理解。

应该注意的问题是，在弹性⼒学中，虽然体⼒和⾯⼒都是⽮量，但是它们均为作⽤于⼀点的⼒，⽽且体⼒是指单位体积的⼒；⾯⼒为单位⾯积的作⽤⼒。

体⼒⽮量⽤F b表⽰，其沿三个坐标轴的分量⽤F b i（i=1，2，3）或者F b x、F b y和F b z表⽰，称为体⼒分量。

描述空间一点的应力状态需要的应力分量应力是描述物体内部力状态的物理量，是单位面积上作用的力，是力对单位面积的作用力。

在空间中，一个点的应力状态可以用应力张量来描述。

应力张量是一个三维矩阵，包含了物体在三个坐标轴上的应力分量。

在三维空间中，一个点的应力状态可以用6个应力分量来描述，分别是xx分量（σxx）、yy分量（σyy）、zz分量（σzz）、xy分量（τxy）、xz分量（τxz）和yz分量（τyz）。

在应力张量中，对角线上的分量（σxx、σyy和σzz）是正应力分量，表示物体沿着各坐标轴方向的内部拉伸或压缩情况。

xz分量（τxz）和yx分量（τyx）是剪应力分量，表示物体在xz和yx平面上的内部剪切力情况。

yz分量（τyz）和xy分量（τxy）也是剪应力分量，表示物体在yz和xy平面上的内部剪切力情况。

应力分量的正负号表示该点的应力状态是拉伸还是压缩，正号表示拉伸，负号表示压缩。

如果某个应力分量为0，则表示该方向上不存在内部拉伸或压缩力。

应力分量的大小表示该方向上的内部力大小。

在实际应用中，应力分量可以通过力分析、力学实验或数值模拟等方法来确定。

不同材料和结构在不同应力状态下会有不同的应力分量，因此我们需要根据具体情况来确定应力分量。

在工程中，应力分量的大小和方向对材料的强度、稳定性和变形等性能有影响。

因此，了解和掌握应力分量的性质和变化规律对设计和优化结构非常重要。

总之，描述空间一点的应力状态需要的应力分量包括正应力分量和剪应力分量，正应力分量描述物体沿各坐标轴方向的内部拉伸或压缩情况，剪应力分量描述物体在不同平面上的内部剪切力情况。

应力分量的大小和方向对材料的性能有重要影响，因此需要根据具体情况来确定应力分量。

描述空间一点的应力状态需要的应力分量应力是描述物体内部受力状态的物理量，空间一点的应力状态包括三个主要应力分量：正应力、剪应力和法向应力。

正应力是指作用于物体某一截面上的垂直于该截面的应力。

在空间中的一点，正应力可以沿着三个坐标轴方向产生，分别称为x方向正应力、y方向正应力和z方向正应力。

这三个应力分量分别用σx、σy和σz表示。

正应力由两部分组成：一部分来自于物体外部对其的作用力，称为外应力或受载应力；另一部分来自于物体内部的分子间作用力，称为内应力或静力应力。

正应力可以使物体沿着这个方向产生形变，例如拉伸、压缩等。

剪应力是指作用于物体某一截面上的平行于该截面的应力。

在空间中的一点，剪应力可以沿着三个坐标轴方向产生，分别称为xy方向剪应力、yz方向剪应力和xz方向剪应力。

这三个应力分量分别用τxy、τyz和τxz表示。

剪应力是由物体外部力矩对其产生的，表现为物体的旋转和扭转。

法向应力是指作用于物体某一截面上的垂直于该截面的应力。

在空间中的一点，法向应力可以沿着各个方向产生，由于其方向多变，没有显式的表示方式。

法向应力可以使物体在垂直于该截面上产生形变，例如变形、弯曲等。

在空间一点的应力状态可以用应力张量来描述。

应力张量是一个二阶对称张量，它包含了全部的应力分量信息。

在直角坐标系下，应力张量的表示形式为：σ = [σx τxyτxz][τxy σy τyz][τxz τyz σz]其中，σx、σy和σz分别表示x方向、y方向和z方向的正应力分量；τxy、τyz和τxz分别表示剪应力的分量。

应力张量可以通过力学分析或实验测量得到。

在工程领域中，了解空间一点的应力状态对于设计和分析结构的强度和稳定性至关重要。

通过合理选择材料和结构形式，可以使结构在应力状态下具有足够的强度和抗变形能力。

因此，研究应力分量及其变化规律对于工程实践具有重要意义。

综上所述，空间一点的应力状态需要考虑正应力、剪应力和法向应力三个应力分量。

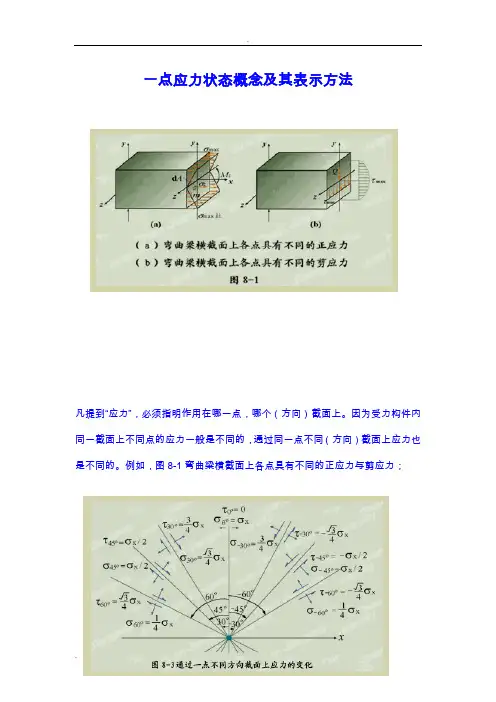
一点应力状态概念及其表示方法凡提到“应力”，必须指明作用在哪一点，哪个（方向）截面上。

因为受力构件内同一截面上不同点的应力一般是不同的，通过同一点不同（方向）截面上应力也是不同的。

例如，图8-1弯曲梁横截面上各点具有不同的正应力与剪应力；图8-2通过轴向拉伸杆件同一点的不同（方向）截面上具有不同的应力。

２．一点处的应力状态是指通过一点不同截面上的应力情况，或指所有方位截面上应力的集合。

应力分析就是研究这些不同方位截面上应力随截面方向的变化规律。

如图8-3是通过轴向拉伸杆件内点不同（方向）截面上的应力情况（集合）３．一点处的应力状态可用围绕该点截取的微单元体（微正六面体）上三对互相垂直微面上的应力情况来表示。

如图8-4（a,b）为轴向拉伸杆件内围绕点截取的两种微元体。

特点：根据材料的均匀连续假设，微元体（代表一个材料点）各微面上的应力均匀分布，相互平行的两个侧面上应力大小相等、方向相反；互相垂直的两个侧面上剪应力服从剪切互等关系。

§8-２平面应力状态的工程实例１．薄壁圆筒压力容器为平均直径，为壁厚由平衡条件得轴向应力：（8-1a）图8-5c（Ⅰ-Ⅰ，Ⅱ-Ⅱ为相距为的横截面，H-H为水平径向面）由平衡条件或, 得环向应力：（8-1b）2．球形贮气罐（图8-6）由球对称知径向应力与纬向应力相同，设为对半球写平衡条件：得（8-2）3．弯曲与扭转组合作用下的圆轴4．受横向载荷作用的深梁§8-3平面一般应力状态分析——解析法空间一般应力状态如图8-9a所示，共有9个应力分量：面上的，，；面上的，，；面上的，，。

1）应力分量的下标记法：第一个下标指作用面（以其外法线方向表示），第二个下标指作用方向。

由剪应力互等定理，有：，，。

2）平面一般应力状态如图8-9b所示，即空间应力状态中，方向的应力分量全部为零（）；或只存在作用于x-y平面内的应力分量，，，，其中，分别为，的简写，而= 。

3）正负号规定：正应力以拉应力为正，压为负；剪应力以对微元体内任意一点取矩为顺时针者为正，反之为负。

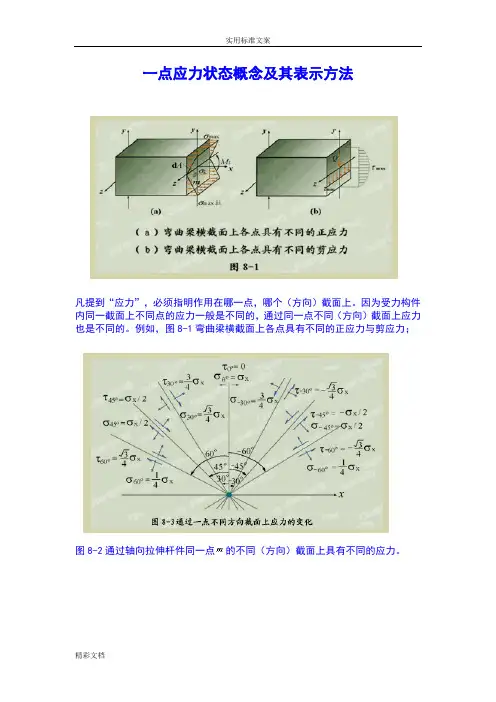
一点应力状态概念及其表示方法凡提到“应力”，必须指明作用在哪一点，哪个（方向）截面上。

因为受力构件内同一截面上不同点的应力一般是不同的，通过同一点不同（方向）截面上应力也是不同的。

例如，图8-1弯曲梁横截面上各点具有不同的正应力与剪应力；图8-2通过轴向拉伸杆件同一点的不同（方向）截面上具有不同的应力。

２．一点处的应力状态是指通过一点不同截面上的应力情况，或指所有方位截面上应力的集合。

应力分析就是研究这些不同方位截面上应力随截面方向的变化规律。

如图8-3是通过轴向拉伸杆件内点不同（方向）截面上的应力情况（集合）３．一点处的应力状态可用围绕该点截取的微单元体（微正六面体）上三对互相垂直微面上的应力情况来表示。

如图8-4（a,b）为轴向拉伸杆件内围绕点截取的两种微元体。

特点：根据材料的均匀连续假设，微元体（代表一个材料点）各微面上的应力均匀分布，相互平行的两个侧面上应力大小相等、方向相反；互相垂直的两个侧面上剪应力服从剪切互等关系。

§8-２平面应力状态的工程实例１．薄壁圆筒压力容器为平均直径，为壁厚由平衡条件得轴向应力：（8-1a）图8-5c（Ⅰ-Ⅰ，Ⅱ-Ⅱ为相距为的横截面，H-H为水平径向面）由平衡条件或, 得环向应力：（8-1b）2．球形贮气罐（图8-6）由球对称知径向应力与纬向应力相同，设为对半球写平衡条件：得（8-2）3．弯曲与扭转组合作用下的圆轴4．受横向载荷作用的深梁§8-3平面一般应力状态分析——解析法空间一般应力状态如图8-9a所示，共有9个应力分量：面上的，，；面上的，，；面上的，，。

1）应力分量的下标记法：第一个下标指作用面（以其外法线方向表示），第二个下标指作用方向。

由剪应力互等定理，有：，，。

2）平面一般应力状态如图8-9b所示，即空间应力状态中，方向的应力分量全部为零（）；或只存在作用于x-y平面内的应力分量，，，，其中，分别为，的简写，而= 。

3）正负号规定：正应力以拉应力为正，压为负；剪应力以对微元体内任意一点取矩为顺时针者为正，反之为负。

一点的应力状态
一点的应力状态是指处于轻微压力下的状态，不会造成明显的紧张或焦虑。

人们常常在工作、学习或日常生活中感受到一点的应力，这种应力可能来自于任务的要求、时间的紧迫或者是自身的期望。

尽管一点的应力有助于提升工作效率和动力，但过度应激或长期处于高强度应激状态可能会对身心健康产生负面影响。

因此，适当的应对和管理一点的应力非常重要，可以通过调节心态、放松身心、寻求支持等方式来缓解压力，保持身心的平衡。

应力是指物体内部受到的力的作用，它可以通过单位面积上的力来描述。

在工程力学中，应力是非常重要的物理量，它与物体的形状、材料特性和外部力的作用密切相关。

本文将围绕应力的概念展开讨论，针对其在材料力学中的应用进行深入分析。

一、应力的定义和分类1.1 应力的概念应力是单位面积上的力，常用符号表示为σ，其计算公式为力F除以面积A，即σ=F/A。

在物体内部，由于外部力的作用，各处都会受到应力的作用，这种应力称为内应力。

而外部施加在物体表面上的力也会导致应力的产生，这种应力称为外部应力。

1.2 应力的分类根据应力的作用方向和大小，可以将应力分为正应力、剪切应力和法向应力三种类型。

正应力是垂直于物体截面的应力，常用符号表示为σn。

而沿着截面方向的应力称为剪切应力，常用符号表示为τ。

另外，法向应力是指作用在物体某一点上的应力。

二、应力状态的描述2.1 应力张量在三维空间中，一个点的应力状态可以由一个3x3的对称矩阵来描述，这个对称矩阵称为应力张量。

应力张量的分量代表了在不同方向上的应力情况，可以通过数学方法进行求解和分析。

2.2 应力状态的表示一个点处的应力状态可以通过应力张量的特征值和特征向量来表示。

特征值代表了应力状态的大小，特征向量则代表了应力作用的方向。

通过对特征值和特征向量的分析，可以判断物体处于何种应力状态，从而进行相应的力学分析和设计。

三、应力的应用3.1 工程材料的性能应力是描述物体受力情况的重要参数，它直接影响着材料的强度、刚度和韧性等性能。

在工程中，通过对材料的应力状态进行分析，可以评估材料的可靠性和安全性，为工程设计提供参考依据。

3.2 结构的稳定性对结构件的受力状态进行分析，可以判断结构在外部载荷作用下的稳定性。

通过对结构的应力分布和应力集中区域的分析，可以预测结构是否会发生破坏或失稳现象，为结构设计和改进提供重要参考。

3.3 力学设计在工程实践中，需要根据实际的力学要求来设计各种零部件和结构件。

第五章 应力状态分析与强度理论一、 内容提要 1.应力状态的概念 1.1一点的应力状态通过受力构件的一点的各个截面上的应力情况的集合，称为该点的应力状态。

1.2一点的应力状态的表示方法——单元体研究受力构件内一点处的应力状态，可以围绕该点取一个无限小的正六面体，即单元体。

若单元体各个面上的应力已知或已计算出，则通过该点的其他任意方位截面上的应力就可用解析法或图解法确定。

1.3主平面、主应力单元体上切应力为零的平面称为主平面，主平面上的正应力称为主应力。

过受力构件内任一点总有三对相互垂直的主平面。

相应的主应力用1σ、2σ、3σ来表示，它们按代数值的大小顺序排列，即321σσσ≥≥。

1σ是最大主应力，3σ是最小主应力，它们分别是过一点的所有截面上正应力中的最大值和最小值。

1.4应力状态的分类（1）单向应力状态，只有一个主应力不为零，另两个主应力均为零； （2）二向或平面应力状态，两个主应力不为零，另一个为零； （3）三向或空间应力状态，三个主应力都不为零。

单向应力状态又称简单应力状态，二向、三向应力状态称为复杂应力状态。

2.平面应力状态分析的解析法在平面应力状态的单元体中，有一对平面上的应力等于零，即为主平面，其上主应力为零。

可将单元体用平面图形表示，如图5-1所示。

图5-12.1任意α斜截面上的应力当已知x σ、y σ、yx xy ττ=时，应用截面法，可得ατασστατασσσσσαα2cos 2sin 22sin 2cos 22xy yx xy yx yx +-=--++= （5-1）式中，正应力以拉应力为正，压应力为负；切应力以对单元体内任意点的矩为顺时针转向为正，反之为负；α为斜截面外法线与x 平面外法线即x 轴间的夹角，α角从x 轴量起，反时针转向为正，反之为负。

2.2主应力22min max 22xy yx y x τσσσσσσ+⎪⎪⎭⎫ ⎝⎛-±+=⎭⎬⎫ （5-2） 式中，max σ和min σ分别表示单元体上垂直于零应力面的所有截面上正应力的最大值和最小值。

一 一点的应力状态与应力张量二 主应力与应力不变量对于一般空间问题，一点的应力状态可以由九个应力分量表示，如P 点处应力状态在直角坐标系可表示为ij S σ==x xy xz yx y yz zx zy z στττστττσ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦如图1-1所示。

在固定受力情况下，应力分量大小与坐标轴方向有关，但由弹性力学可知，新旧坐标的应力分量具有一定变换关系。

通常，我们称这种具有特定变换关系的一些量为张量。

式（1-1）就是应力张量，它是二阶张量。

因为它具有xz τ=zx τ，xy τ=yx τ，yz τ=zy τ。

已知物体内某点P 的九个应力分量，则可求过该点的任意倾斜面上的应力。

在P 点处取出一无限小四面体oabc (图1-2)它的三个面分别与x,y,z 三个轴相垂直。

另一方面即任意斜面，它的法线N ，其方向余弦为l,m,n 。

分别以dF 、x dF 、y dF 、z dF 代表abc 、obc 、oac 、 oab 三角形面积。

x y z dF ldF dF mdF dF ndF ⎫=⎪=⎬⎪=⎭（1.2）在三个垂直于坐标的平面上有应力分量，在倾斜面abc 上有合应力N P ,它可分解为正应力N σ及切向剪应力N τ，即222N N N P στ=+N P 沿坐标轴方向分量为N x ,N y ，N z ，由平衡条件可得N x xy xz N yx y yz N zx zy z x l m n y l m n z l m n στττστττσ⎫=++⎪=++⎬⎪=++⎭求出N x ，N y ，N z 在法线上的投影之和，即得正应力N σ222222N N N N x y z xy yz zx x l y m z n l m n lm mn nl σσσστττ=++=+++++ 1-5而剪应力则由式1-5得 2N τ=2N P -2N σ在空间应力状态下一点的应力张量有三个主方向，三个主应力。