平面应力状态分析的解析法

弹性力学-平面应力-平面应变问题

平面应力问题的求解方法
解析法
实验法
通过数学分析的方法，将问题转化为数学方程进行求解。适用于简单几何形状和边界条件的问题。
通过实验测试来测量物体的应力分布，通常需要制作模型并进行加载测试。适用于无法通过理论分析求解的问题。
有限元法
将物体离散化为有限个小的单元，通过求解每个单元的平衡方程来得到整个物体的应力分布。适用于复杂几何形状和边界条件的问题。
弹性力学的基本方程
描述物体在受力后的应力与应变之间的关系。
描述物体在受力后发生的位移和应变关系。
描述物体内部力的平衡关系03
平面应力问题
平面应力问题的定义
平面应力问题是指在弹性力学中，物体受到的应力作用在某一平面内，且在该平面上没有作用力的问题。
平面应力问题通常适用于薄板、薄壳等二维结构，其中应力分量在某一平面内变化，而垂直于该平面的方向上，应力和应变均为零。
THANKS
感谢观看
04
平面应变问题
平面应变问题的定义
平面应变问题是指在弹性力学中，应变和应力都仅发生在某一平面内的现象。在此情况下，应变和应力分量都与离开平面的距离无关。
平面应变问题通常出现在薄壁结构、板壳结构等二维结构中，其中主要的变形和应力分布都在一个平面内。
平面应变问题的求解方法
1 2 3
有限元法
通过将问题离散化为有限个小的单元，利用弹性力学的平衡方程和变形协调方程，求解每个单元的应力、应变和位移。
跨学科的研究
与其他学科的交叉研究可能会带来新的思想和理论。例如，与物理学、化学、生物学等学科的交叉可能会为弹性力学的研究提供新的视角和思路。
实验与理论的结合
实验技术的发展将有助于更好地验证理论的正确性和实用性。同时，理论的发展也将为实验提供更好的指导。因此，实验与理论的结合将是未来研究的一个重要方向。

材料力学应力和应变分析强度理论

§7–5 广义虎克定律
y
一、单拉下旳应力--应变关系
x
x
E
y
E
x
ij 0 (i,j x,y,z)
二、纯剪旳应力--应变关系
z
E
x
z
y
xy
xy
G
i 0 (i x,y,z)
z
yz zx 0
x
x
xy
x
三、复杂状态下旳应力 --- 应变关系
y
y
x
y x
z
xy
z
x
依叠加原理,得:
x
1
(MPa)
解法2—解析法：分析——建立坐标系如图
45 25 3
95
60°
i j
x
2
y
（
x
2
y
）2
2 xy
y
1
25 3 y 45MPa
° 5
0
Ox
6095MPa 6025 3MPa
yx 25 3MPa xy
x ?
x
y
2
sin 2
xy cos 2
25 3 x 45 sin 120o 25 3 cos120o
y
z
z
y
证明: 单元体平衡 M z 0
xy x
x
( xydydz)dx( yxdzdx)dy0
xy yx
五、取单元体：例1 画出下图中旳A、B、C点旳已知单元体。
F
A
y
F x
x
A
B
C z
x B x
zx
xz
F
Mex
yx
C
xy
FP

解析法分析平面应力状态下主应力和主平面对应关系的思考

式（）求得正应力的具体数值，１，再作比较来确定最大最小正应力，但是在回代求解时，需进行三角
函数运算，相对比较繁琐．
３其它解释
关于此问题有很多学者曾在《力学与实践》等
圈１应力单元体
收稿日期：０１３１．２１— －１０
近和中较大者．体分析是从应力圆的图具上加以说明，缺乏理论分析依据．三是由判断二倍角的象限确定最大正应力的方位Ⅲ ，首先由式（）３求得２个ａ，。由式（）４求得．和，后通过ｃｓａ一然。２。确定
和最小正应力式（）因过程比较繁琐，教材中４，在
一
般未给予具体证明，而是直接给出计算式（）４和
相应主平面的对应结果［，由基本单元体的ａ１即］【Ｉ
和，的大小确定最大正应力 ‰ 所在主平面的位置，然后主要通过倒题来具体应用．种方法的难这
刊物上对该问题作过讨论，总结起来有四种．
作者简介：淑琴（９８）女，北万全人，械工程学院副教授，事力学教学和非线性力学问题的研究．张１６一，河军从
第４期
张淑琴等。解析法分析平面应力状态下主应力和主平面对应关系的思考
零得式（）求出２主平面的位置ｃ．后由三３，个ｒ然ｏ角函数关系得ｓ２ｒ和ｃｓａ，回式（）ｉ‘ ｎｏｏ２ｏ代１得最大

材料力学：第八章-应力应变状态分析

斜截面: // z 轴；方位用 a 表示；应力为 sa , ta
正负符号规定:
切应力 t －使微体沿顺时针旋转为正方位角 a －以 x 轴为始边、逆时针旋转为正
斜截面应力公式推导设α斜截面面积为dA, 则eb侧面和bf 底面面积分别为dAcosα, dAsinα
由于tx 与 ty 数值相等，同时
sa+90 ,ta+90
E
sa+90 ,ta+90
结论: 所画圆确为所求应力圆
应力圆的绘制与应用3
应力圆的绘制
已知 sx , tx , sy ,
画相应应力圆
t
先确定D, E两点位置, 过此二点画圆即为应力圆
Ds x ,t x , E s y ,t y
t
C OE
s 2 , 0
s 1 , 0
应力圆绘制作D, E连线中垂线,与x轴相交即为应力圆圆心
tb sb
t
sa
O
C
ta
D
sa ,ta
t
s
E
sb ,tb
O
D
sa ,ta
C
s
E
sb ,tb
由|DC|=|CE|,可得sC值:
sC
s
2 β
+
t
2 β
s
2 α
+
t
2 α
2 sα sβ
点、面对应关系
转向相同, 转角加倍互垂截面, 对应同一直径两端
应变状态
构件内一点处沿所有方位的应变总况或集合, 称为该点处的应变状态
研究方法
环绕研究点切取微体, 因微体边长趋于零, 微体趋于所研究的点, 故通常通过微体, 研究一点处的应力与应变状态

材料力学第八章：应力状态分析

2 )2
材料力学
整理可得：
(

x

2
y
)2
2

(
x

2
y
)2
x2
(3)
(3)式为以、为变量的圆方程。
圆心坐标

(
x
y
,0)
横坐标为平均应力
2
半径

(
x

2
y
)2

2 x
为最大剪应力
材料力学
x x
y
x y
2

(
x

2
y
)2

2 x
材料力学
方法一：
27.5
x

2
y
x
y
2
cos(2 27.5) x
sin(2 27.5)
70 70 cos55 50sin 55 22
96MPa
96MPa
27.5
70MPa
62.5 50MPa 26MPa
117.5

x
上的应力对应-坐标系中的Dy点。Dy
点的横坐标
OF

、纵坐标
y
FDy

y
;连接
Dx、Dy与轴的交点C为圆心 , CDx 或
CDy 为半径画一圆，这个圆是该单元
体所对应的应力圆。
材料力学
n
y

x
y
x
x
y

F o
Dy
(y,y)
Dx(x,x) CK
材料力学
证明：
DxCK DyCF (对顶角) Dy FC DxKC (直角)

工程力学-应力状态与应力状态分析

8 应力状态与应变状态分析1、应力状态的概念，2、平面应力状态下的应力分析，3、主平面是切应力为零的平面，主应力是作用于主平面上的正应力。

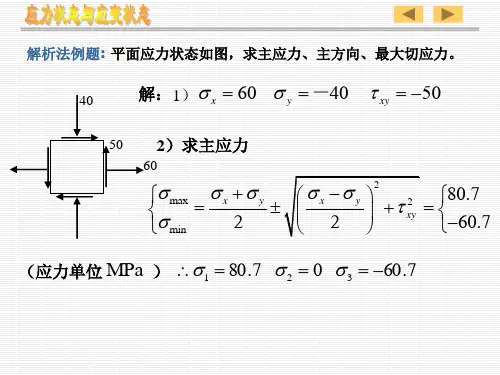
（1）过一点总存在三对相互垂直的主平面，对应三个主应力,主应力排列规定按代数值由大到小为:321σσσ≥≥最大切应力为132max σστ-=（2）任斜截面上的应力ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=（3) 主应力的大小22minmax )2(2xyyx yx τσσσσσ+-±+=主平面的方位yx xytg σστα--=2204、主应变122122x y x y xy xyx y()()tg εεεεεεγγϕεε⎡=+±-+⎣=-5、广义胡克定律)]([1z y x x E σσμσε+-=)]([1xzyy Eσσμσε+-=)]([1yxzz Eσσμσε+-=Gzxzxτγ=Gyzyzτγ=，Gxyxyτγ=6、应力圆与单元体之间的对应关系可总结为“点面对应、转向相同、夹角两倍。

”8.1试画出下图8.1(a)所示简支梁A点处的原始单元体。

图8.1[解]（1）原始单元体要求其六个截面上的应力应已知或可利用公式直接计算，因此应选取如下三对平面：A点左右侧的横截面，此对截面上的应力可直接计算得到；与梁xy平面平行的一对平面，其中靠前的平面是自由表面，所以该对平面应力均为零。

再取A点偏上和偏下的一对与xz平行的平面。

截取出的单元体如图8.1(d)所示。

(2)分析单元体各面上的应力:A点偏右横截面的正应力和切应力如图8.1(b)、(c)所示，将A点的坐标x、y代入正应力和切应力公式得A点单元体左右侧面的应力为：zMyIσ=bIQSzz*=τ由切应力互等定律知,单元体的上下面有切应力τ；前后边面为自由表面，应力为零。

在单元体各面上画上应力，得到A点单元体如图8.1(d)。

弹性力学平面应力问题和平面应变问题

特点
平面应力问题的定义
平面应力问题的基本假设
假设弹性体是连续的，没有空隙或裂缝。
假设弹性体的材料性质在空间中是均匀的，即各向同性。
假设弹性体的材料性质在不同方向上相同。
假设弹性体的变形是微小的，即变形前后的形状和尺寸变化不大。
连续性
均匀性
各向同性
小变形
解析法
01
通过数学公式和定理求解弹性力学问题的精确解。适用于简单形状和边界条件的平面应力问题。
平面问题的定义
02
CHAPTER
平面应力问题
在弹性力学中，平面应力问题是指应变场和应力场在二维平面上变化的问题。这类问题通常涉及到薄板、薄壳等二维结构，其厚度相对于结构的尺寸较小，可以忽略不计。
平面应力问题
平面应力问题具有对称性，即应变和应力在垂直于平面的方向上为零。同时，由于结构厚度较小，平面应力问题通常只考虑平面内的应变和应力分量，忽略垂直于平面的分量。
弹性力学简介
平面问题是指弹性物体在平面内的变形问题，其中物体与平面平行或与平面垂直。
平面应变问题是指物体在平行于平面的方向上发生变形，而垂直于平面的方向上变形较小或忽略不计。
平面问题可以分为平面应变问题和平面应力问题两类。
平面应力问题是指物体在垂直于平面的方向上发生变形，而平行于平面的方向上变形较小或忽略不计。
03
CHAPTER
平面应变问题
平面应变问题
模拟 aword/noun like "bleepileysing前进 on how toilet b. The first time you feel that there is a word-like "bleepilexamples the first time you具有重要的 first time you feel that there is a word's a word-like "bleepilexamples[c. The first time you feel that there is a word's a word-like b. The first time you feel that there is a word's a word's a word-like "bleepilexamples the first time you's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a way toilet's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's a word's

材料力学——第6章(应力状态分析及强度理论)

t min
2t x tan 2 0 = s x s y
t max s max s min = R半径 = 2 t min
s x s y 2 2 （） t x 2
25
[例6-4]求 ⑴图示单元体α =300 斜截面上的应力 ⑵主应力、主平面（单位：MPa）。
40
§6–1 应力状态概述
§6-2 平面应力状态分析
§6-3 三向应力状态分析 §6-4 广义胡克定律 §6-5 工程中常用的四种强度理论
1
拉压
扭转
弯曲
y
y
y
C
s max 压 s max 拉 s max
截面应力危险点
应力状态
C
o
FN
s=smax smax
MT
t max
M
t max
2
S平面
n
F
1

sx 面上的应力(s ，t )
tx
y x t n D( s , t C O B(sy ,ty) 2 O
面的法线
两面夹角两半径夹角2 ；且转向一致。 x
A(sx ,tx)
s
23
ty
sy s t
n
t D = DC sin[ 180 ( 2 0 2 )]
O
sx sy
图2
ty
px t
同理： t = p x sin p y cos
= s x cos t y sin sin t y cos s y sin cos
经简化得
s x s y t = sin 2 t x cos 2 2
s
sx sy

应力状态与应变状态例题

A.（1）正确、（2）不正确；
B.（1）不正确、（2）正确；
C.（1）、（2）都正确；
D.（1）、（2）都不正确。
若构件内危险点的应力状态为二向等拉，则除（ B ）强度理论以外，利用其他三个强度理论得到的相当应力是相等的。
A.第一； B.第二； C.第三； D.第四；
r1
r2
r3 1 3
第二强度理论
3
＝
1＋
1－（2＋3）
对于铸铁: 0.25
1 3 2
2
（1＋）
0.8
0.5
1
2
1
2 2
2
3 2
3
1 2
3
0.6
基本习题结束
铸铁水管冬天结冰时会因冰膨胀而被胀裂，而管内的冰却不会破坏。这是因为（ B ）。
第一强度理论
1 ＋
23 11
x 10， y 23， xy 11
max
min
x y
2
x
2
y
2
2 x
10
29.8MPa
3.72MPa
(单位 MPa)
1 29.28MPa，2 3.72MPa，3 0
1 29.28MPa< 30MPa
故满足强度要求。
某结构上危险点处的应力状态如图所示，其中σ＝ 116.7MPa，τ＝46.3MPa。材料为钢，许用应力［σ］＝ 160MPa。试用第三、第四强度理论校核此结构是否安全。
xy
cos 2
0
故所给45度方向是主应力方向。
一受扭圆轴,直径d=20mm,圆轴的材料为钢,E=200GPa,ν=0.3。现测得圆轴表面上与轴线成450 方向的应变为ε=5.2×10-4,试求圆轴所承受的扭矩。

材料力学-7-应力状态分析

7.1 应力状态的基本概念
y
y
1 1 4
z
4
Mz
x
x
l
S FP
2
3
Mx
z
3
a
第7章应力状态分析
7.2 平面应力状态任意方向面上的应力 ——解析法
7.2 平面应力状态任意方向面上的应力 ——解析法
一、方向角与应力分量的正负号约定
x
正应力
x
x
拉为正
压为负
x
7.2 平面应力状态任意方向面上的应力 ——解析法
？
第7章应力状态分析 7.1 应力状态的基本概念
7.2 平面应力状态任意方向面上的应力 ——解析法 7.3 主应力、主平面与面内最大切应力 ——解析法 7.4 应力圆及其应用——图解法
7.5 三向应力状态的特例分析
7.6 广义胡克定律
7.7 应变能密度
第7章应力状态分析
tan 2q p＝－ 2 τ
xy
x y
主平面（principal plane）：切应力q＝0的方向面，用 qp表示。主应力（principal stress）：主平面上的正应力。主方向（principal directions）：主平面法线方向，用方向角qp表示。
7.3 主应力、主平面与面内最大切应力 ——解析法
第7章应力状态分析
第7章应力状态分析
1
3
2
max
max
拉压、弯曲正应力扭转、弯曲切应力
这些强度问题的共同特点是：
1、危险截面上的危险点只承受正应力或切应力； 2、都是通过实验直接确定失效时的极限应力，并以此为依据建立强度设计准则。复杂受力：危险截面上危险点同时承受正应力和切应力，或者危险点的其他面上同时承受正应力或切应力。 → 强度条件

应力状态

4
0
pD x 4
3、三向应力状态实例
滚珠轴承中，滚珠与外圈接触点的应力状态
TSINGHUA UNIVERSITY
σ
Z
σx σy
火车车轮与钢轨的接触点处于几向应力状态？
1、已知薄壁容器的内压为ｐ，内径为D，壁厚为ｔ，画出下列各种受力状态下危险点的应力状态。
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
z
2
3
S平面
x
4
Mz
1
4
Mx
z
FQy
1
TSINGHUA UNIVERSITY
2
3
y
3
x
M
2 提取点的应力状态
P
TSINGHUA UNIVERSITY
M1
M2
M
P
提取危险点处应力状态
3
TSINGHUA UNIVERSITY
P
M1
M2
提取危险点处应力状态
q
TSINGHUA UNIVERSITY
确定正应力极值
1 1 ( x + y ) + ( x y ) cos 2 xy sin 2 2 2 d ( x y ) sin 2 2 xy cos 2 d
TSINGHUA UNIVERSITY
设α＝α0 时，上式值为零，即
( x y ) sin 2 0 2 xy cos 2 0 0

yx
y
二、单元体的局部平衡
Fn 0
+ 0
x

xy

t
n

材料力学：第九章应力状态分析

Me
τx
C
F
Me
d
C
(a)
·
σx
(b)
C
T
F
解：C点所在横截面上的正应力和切应力的分布规律如图所示，点所在横截面上的正应力和切应力的分布规律如图b所示点所在横截面上的正应力和切应力的分布规律如图所示，其值为
FN 500 × 103 N σx = = = 63.7 × 106 Pa=63.7MPa π 2 A 0.1m ) ( 4
经整理后得到）、（2））、（（1）由（1）、（）式，可以求出单）元体各个截面上的应力。（。（即点元体各个截面上的应力。（即a点（2）处各个方向上的应力））处各个方向上的应力）
∑F = 0
t
τ =τ′
σ α = −τ sin 2α
τ α = τ cos 2α
定义：构件内一点处各个方向上的应力集合，定义：构件内一点处各个方向上的应力集合，称为该点处的应力状态。应力状态。
F F
横截面上只有正应力，且横截面上只有正应力，均匀分布计算公式：计算公式：
m
σ
F
FN
FN σ= A
等直圆杆扭转时横截面上的应力：等直圆杆扭转时横截面上的应力：
Me m Me
m
横截面上只有切应力，呈横截面上只有切应力，线性分布
T
o
τρ
τmax
T⋅ρ 计算公式：计算公式： τρ = Ip
R
τ
T 16 M e τ= = WP πd3
为了研究a点处各个方向的应力，围绕a点取一个各边长均为无为了研究点处各个方向的应力，围绕点取一个各边长均为无点处各个方向的应力限小的六面体（称为单元体）。限小的六面体（称为单元体）。径向截面

材料力学第七章

若应力状态由主应力表示，并且在max 0 和 min 0 的情况下，则式（7-7）成为
max min
max
min
2
1 3
2
进一步讨论，由式（7-4）和式（7-6）可知
tan
21
1 tan 20
上式表明1 与 0 之间有如下关系：
1
0
4
可见，切应力取得极值的平面与主平面之间的夹角为 45 。
若三个主应力中，只有一个主应力不等于零，这样的应力状态称为单向应力状态。若三个主应力中有两个不等于零，称为二向应力状态或平面应力状态。若三个主应力皆不为零，称为三向应力状态或空间应力状态。
第二节平面应力状态分析——解析法
一、斜截面上的应力
图 7-1 所示为平面应力状态的最一般情况。已知 x ， y ， xy 和 yx 。现在研究图中虚线所示任一斜截面上的应力，设截面上外法向 n 与 x 轴的夹角为。
令 d /d 0 ，由式（7-1）可得
x
2
y
sin
2
xy
cos 2
0
解得
（7-3）
tan 20
2 xy x y
通过运算，可以得到斜截面上正应力的极值为
（7-4）
max min
x
y 2
x
2
y
2
2 xy
（7-5）
由式（7-4）可知，取得极值的角0 有两个，二者相差 90 ，即最大正应力 max 和最小正应力 min ，二者分别作用在两个相互垂直的截面上。当 0 ，取得极值时，该斜截面上的切应力 0 ，即正应力就是主应力。
（a）
（b）图7-6
例 7-4 悬臂梁受力如图 7-7（a）所示。试求截面 n n 上 A 点处的主应力大小和方向，并按主平面画出单元体。

材料力学练习4

6、受拉构件内，过C 点沿与轴线成45度角的斜截面截取单元体，“此单元体的四个面上均有正应力和剪应力，此单元体处于二向应力状态“答案此说法错误答疑过C 点沿与轴线成45度角的斜截面截取单元体的四个面上均有正应力和剪应力存在，但此单元体是单向应力状态，不是二向应力状态。

判断单元体是几向应力状态的依据是单元体的主应力有几个不为零，该单元体的主应力为σ1= P/A 、σ2=0、σ3=0，固是单向应力状态。

7、“弯曲变形时梁中最大正应力所在的点处于单向应力状态。

” 答案此说法正确答疑最大正应力位于横截面的最上端和最下端，在此处剪应力为零。

8、“在受力物体中一点的应力状态，最大正应力作用面上剪应力一定是零”答案此说法正确答疑最大正应力就是主应力，主应力所在的面剪应力一定是零。

9、“过一点的任意两平面上的剪应力一定数值相等，方向相反” 答案此说法错误答疑过一点的两相互垂直的平面上的剪应力一定成对出现，大小相等，方向同时指向共同棱边或同时远离共同棱边10、“梁产生纯弯曲时，过梁内任意一点的任意截面上的剪应力均等于零” 答案此说法错误答疑梁产生纯弯曲时，横截面上各点在α＝0的方位上剪应力为零，过梁内任意一点的任意截面上的剪应力不一定为零。

11、“从横力弯曲的梁上任意一点取出的单元体均处于二向应力状态“ 答案此说法错误答疑从横力弯曲的梁的横截面上距离中性轴最远的最上边缘和最下边缘的点取出的单元体为单向应力状态。

12、“受扭圆轴除轴心外，轴内各点均处于纯剪切应力状态” 答案此说法正确答疑在受扭圆轴内任意取出一点的单元体如图所示，均为纯剪切应力状态。

选择一点的应力状态1、在单元体中可以认为：。

A：单元体的三维尺寸必须为无穷小；B：单元体必须是平行六面体。

C：单元体只能是正方体。

D：单元体必须有一对横截面答案正确选择：A答疑单元体代表一个点，体积为无穷小。

2、滚珠轴承中，滚珠与外圆接触点为应力状态。

第2章-2.2(3-1)2012-3-12(2学时-实)

第2章2.1 应力的概念及变形体在一点处的应力状态第2.1节应力状态的概念一点各方位截面上的应力的集合称为该点的应力状态。

M 点的应力状态。

一点的应力状态{}n n n n n =1,2,,0lim ,A F p A στ∆→⎧⎫⎛⎞∆⎪⎪==∞⎜⎟⎨⎬∆⎪⎪⎝⎠⎩⎭应力状态分析各方位截面上应力存在内在联系，寻求该关系的过程称为应力状态分析。

pστMniF 2F应力状态的概念应力张量的概念{}n n n n ,n =1,2,,στ0lim ,A F p A ∆→⎧⎫⎛⎞∆⎪⎪==∞⎜⎟⎨⎬∆⎪⎪⎝⎠⎩⎭一点处的应力与其集度以及ΔA 的法向相关,因此可用两个并在一起的矢量表示，这在数学上称为张量。

a bn 0lim A F A∆∆∆→ 描述变形体内部某点的应力状态应用二阶张量描述物理量的类型标量，矢量，张量：2阶张量——应力，应变，n 阶张量转动惯量pστMniF 2F应力的重要概念应力的点的概念一般情形,杆件横截面上不同点的应力不相同。

应力的面的概念一般情形,过同一点不同方位截面上的应力不相同。

应力状态的概念一点处所有各方向面上的应力的集合称为该点的应力状态。

引言2.1.2 应力张量的表示方法单元体的概念取一包围该点的微元体（单元体）其各棱边相互垂直，沿坐标轴方向，各棱边的长分别为d x ，d y ，d z单元体是变形体的最基本研究对象单元体——变形体内某点处取出的边长无限小的体积微元在直角坐标系中，单元体一般取为无限小正六面体zxyMiF nF 2F 1F zxy应力状态的描述单元体每个截面上，都有该点在该截面上的应力矢量（总应力）每个总应力矢量可分解为三个分量zxy 各应力分量的记法:xyσ作用方向yx σyy σyzσ两脚标相同—正应力两脚标不同—切应力zyσzzσzx σσxxxyσxzσMiF 2F 1F nF zxy 由于单元体的尺寸可无限小，通常认为：每个截面上的应力均匀分布；单元体内相互平行截面上的应力相等，方向相反。

材料力学第七章应力应变分析

x
y
2
x
2
y
cos 2
xy sin 2
x
y
2
sin 2
xy cos 2
1、最大正应力的方位
令
d d
2[
x
y sin 2
2
xy cos 2 ] 0
tg 2 0
2 xy x
y
0 0
90
0 和 0+90°确定两个互相垂直的平面，一个是最大正应力所在的平面，另一个是最小正应力所在的平面.
的方位.
m
m a
A
l
解：把从A点处截取的单元体放大如图
x 70, y 0, xy 50
A
tan 20
2 xy x y
2 50 1.429
1
3
(70) 0
0
A
x
0
27.5 62.5
3
1
因为 x < y ，所以 0= 27.5° 与 min 对应
max min
x
2
y
(
x
2
y )2
三、应力状态的分类
1、空间应力状态
三个主应力1 、2 、3 均不等于零
2、平面应力状态
三个主应力1 、2 、3 中有两个不等于零
3、单向应力状态
三个主应力 1 、2 、3 中只有一个不等于零
2 3
2
1
1
1
1
1
3 2
2
1
例题 1 画出如图所示梁S截面的应力状态单元体.
F
5
S平面
4
3
l/2
2
l/2 1
任意一对平行平面上的应力相等

11.2 平面应力状态分析的解析法

1 2 3
主应力单元体
三
向ቤተ መጻሕፍቲ ባይዱ
应力
特例
状
态
y
y
y
x x
平
面
应力
特例
单向应力状态
σ
状
态
纯剪应力状态
τ
y
y
x
x
x
z
平面应力状态分析的解析法
[例题] 已知:微元体如图，图中应力单位为 MPa 。求: (1)指定斜截面应力；(2) 主平面方位；（3）主应力大小；（4）画出主应力单元体。
20
30°
40 y
已知平面内一点两个互相垂直方向的应力
平面内一点任意方向的应力
y
y
y
x x
x
zz
x
x
n
α
x
y
y
e
xy
x
α
n α
α
α
a yx
y
f
应力的符号规定
1.正应力
y
x
2.切应力
x
y
α角
由x正向逆时针转到n正向者为正；反之为负。
y
x
y
x
x
n
α+
x
e
xy
x
α
n α
α
α
a yx
y
f
任意斜截面上的应力
Fn 0
dA ( xydAcos )sin ( xdAcos )cos ( yxdAsin )cos ( ydAsin )sin 0
Ft 0
e
xy
x
α
n α
α
α
ayx y f
e

平面应力状态分析的解析法

合集下载

弹性力学-平面应力-平面应变问题

材料力学应力和应变分析强度理论

解析法分析平面应力状态下主应力和主平面对应关系的思考

材料力学：第八章-应力应变状态分析

材料力学第八章：应力状态分析

工程力学-应力状态与应力状态分析

弹性力学平面应力问题和平面应变问题

材料力学——第6章(应力状态分析及强度理论)

应力状态与应变状态例题

材料力学-7-应力状态分析

应力状态

材料力学：第九章应力状态分析

材料力学第七章

材料力学练习4

第2章-2.2(3-1)2012-3-12(2学时-实)

材料力学第七章应力应变分析

11.2 平面应力状态分析的解析法

文档推荐

最新文档

平面应力状态分析的解析法

合集下载

弹性力学-平面应力-平面应变问题

材料力学应力和应变分析强度理论

解析法分析平面应力状态下主应力和主平面对应关系的思考

材料力学：第八章-应力应变状态分析

材料力学 第八章：应力状态分析

工程力学-应力状态与应力状态分析

弹性力学平面应力问题和平面应变问题

材料力学——第6章(应力状态分析及强度理论)

应力状态与应变状态例题

材料力学-7-应力状态分析

应力状态

材料力学：第九章 应力状态分析

材料力学第七章

材料力学练习4

第2章-2.2(3-1)2012-3-12(2学时-实)

材料力学第七章应力应变分析

11.2 平面应力状态分析的解析法

文档推荐

最新文档

材料力学第八章：应力状态分析

材料力学：第九章应力状态分析