清华大学电路原理考研真题

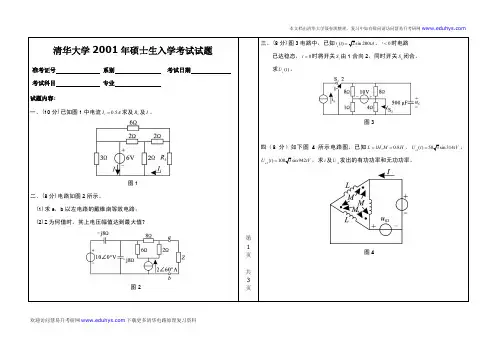
2013年清华大学827电路原理考研试题
回忆版）
）
电路原理考研试题（
（回忆版
第一题第一小问为理想变压器，求电压源有功功率问题，用到了并联谐振知识，第二给了激励图形，和h(t)图形，求响应r(t),用卷积积分求，我直接拉氏变换相乘之后再变过来。

第二题为三相电路，第一小问很普通的求电流求法，第二小问两表法测功率，第三小问z1对中性点电路，求三相电源有功功率，结果第三问没有看明白怎么个意思，果断跳过。

第三题为放大器，用到虚短虚断。

第四题电路原理的应用，用到了互易定理，特勒根，叠加。

感觉第四章基本上都用到了吧。

第五题为列写状态方程，起初想用回流法弄出来，后来感觉太麻烦了，用了直接法搞定
第六题忘记了
第七题为时域方程，二阶电路，直接套入方法可以求出方程，这题总共有三问，图形结合二极管，先是构成一个二阶电路，后又变成一阶电路，第一
问是问两个阶段状态，第二问是问电感电流什么时候最大，最大是多少，第三问是问如果电感可以调，怎么调才能使达到最高电路时间缩短一半，验证。

第八题为复域运算，套入拉氏变换，求Uc电压，结点法搞定
第九题传递函数，结合非线性电路，外加叠加定理，直流交流的应用，基础，但是运算量大
第十题网络图论，也是基础。

第十一题分布电路求电阻。

电路原理考研试题及答案### 电路原理考研试题及答案一、选择题1. 在电路中，当电阻R与电容C串联后，通过电阻的电流与通过电容的电流相位关系是（）。

- A. 同相- B. 超前90°- C. 滞后90°- D. 无相位关系2. 一个理想变压器的原边电压为220V，副边电压为110V，若原边电流为1A，则副边电流为（）。

- A. 0.5A- B. 1A- C. 2A- D. 4A3. 电路中，当电感L与电阻R串联，接在直流电源上，电感L的瞬时电流表达式为（）。

- A. \( i(t) = \frac{E}{R} \)- B. \( i(t) = \frac{E}{R} (1 - e^{-\frac{Rt}{L})} \)- C. \( i(t) = E(1 - e^{\frac{Rt}{L})} \)- D. \( i(t) = E(1 - e^{-\frac{Rt}{L}}) \) / L二、填空题1. 电路的功率因数是指电路中视在功率与有功功率的比值，通常用________表示。

2. 一个电路的等效电阻为10Ω，当通过的电流为2A时，其功率为________W。

3. 理想二极管的伏安特性为：正向导通时，电压几乎为零；反向截止时，电流几乎为________。

三、计算题1. 已知电路中有两个电阻R1和R2串联，其电阻值分别为6Ω和4Ω。

当电路两端电压为12V时，求通过R1的电流I1。

2. 考虑一个含有电感L和电阻R的RLC串联谐振电路，已知L=0.5H，C=100μF，R=10Ω。

计算电路的谐振频率，并求谐振时电路的电流。

四、简答题1. 简述什么是电路的最大功率传输定理，并说明其应用。

2. 解释什么是电路的暂态过程，并举例说明其在实际电路中的应用。

答案一、选择题1. 答案：C. 滞后90°2. 答案：C. 2A3. 答案：B. \( i(t) = \frac{E}{R} (1 - e^{-\frac{Rt}{L})} \)二、填空题1. 答案：cosφ2. 答案：40W3. 答案：零三、计算题1. 解：通过R1的电流I1与R2的电流I2相等，由欧姆定律得：\[ I1 = I2 = \frac{V}{R1 + R2} = \frac{12V}{6Ω + 4Ω} = 1.5A \]2. 解：谐振频率f0由以下公式计算：\[ f_0 = \frac{1}{2\pi \sqrt{LC}} \]将给定的L和C值代入，得：\[ f_0 = \frac{1}{2\pi \sqrt{0.5 \times 10^{-3} \times 100 \times 10^{-6}}} \]计算得f0的值。

清华大学硕士电路原理-20(总分：100.00，做题时间：90分钟)一、解答题(总题数：11，分数：100.00)1.试将戴维南定理推广，导出由线性电阻和独立电源组成的有源双口网络的最简单的等效电路，说明怎样通过测量外部的电压、电流来确定等效电路中的元件数值。

将所得结果用于下图所示的双口网络，求出它的最简单的等效电路。

（分数：8.00）__________________________________________________________________________________________ 正确答案：()解析：解对含独立电源的一端口网络，根据戴维南定理可等效为电压源和电阻串联电路(图(a)所示电路)。

(a)其电压、电流关系为U=R i I+U o，U o为含独立电源一端口网络的开路电压。

对含独立电源的二端口网络(图(b)所示电路)，可得类似的矩阵形式关系式：(b)其等效电路如图(c)或图(d)所示。

(c)(d)其中，R 1、R 2、R 3为对应无源二端口的T型等效电路中的参数；R a、R b、R c为对应无源二端口的Ⅱ型等效电路中的参数。

U o1、U o2为含源二端口两个端口开路时的端口电压。

应用上述结果计算上图所示二端口的T型等效电路(如图(d)所示)或Ⅱ型等效电路(如图(d)所示)的参数，所得结果如下：2.下图所示电路中，二端口网络N的传输参势求负载电阻R 2为何值时其上获得最大功率?并求此最大功率。

（分数：8.00）__________________________________________________________________________________________ 正确答案：()解析：解利用两个二端口的级联，原电路可等效为图(a)所示电路。

(a)其中二端口网络N"传输参数矩阵其传输参数方程为求戴维南等效电路(图(b)所示电路)：开路电压为I 2 =0时的电压U 2，即(b)等效电阻为独立源置零时，端口2的入端电阻当R 2 =R i =4.33Ω时获得最大功率，此最大功率为3.已知下图(a)中二端口N的传输参数为R为非线性电阻，其伏安特性如图(b)所示。

清华大学硕士电路原理-15(总分：100.00，做题时间：90分钟)一、解答题(总题数：10，分数：100.00)1.求下列函数f(t)的象函数。

(1)f(t)=1+2t+3e -4t(2)f(t)=3te -5t(3)f(t)如下图所示。

（分数：10.00）__________________________________________________________________________________________ 正确答案：()解析：解已知原函数f(t)，求其象函数F(s)可利用拉普拉斯正变换(以下简称拉氏变换)的定义式，或直接利用常用函数的拉普拉斯变换式及变换的性质。

用定义求象函数较繁，而一般给定的原函数是常用函数，可利用变换结果和一些变换的性质直接求象函数。

(1)直接利用常用函数的拉氏变换结果得(2)直接利用常用函数的拉氏变换结果得(3)先由题目中的图写出函数的时域表达式为f(t)=t[ε(t)-ε(t-1)]+[ε(t-1)-ε(t-2)]=tε(t)-(t-1)ε(t-1)-ε(t-2)利用常用函数的拉氏变换结果和时域的平移性质得其象函数为(1).求函数f(t)=1+2e -4t +3te -5t的象函数。

（分数：5.00）__________________________________________________________________________________________ 正确答案：()解析：解(2).函数f(t)为e -t在0～2s之间的波形，如下图所示，求f(t)的象函数。

（分数：5.00）__________________________________________________________________________________________ 正确答案：()解析：解由题目中的图写出函数f(t)的时域表达式为f(t)=e -t [ε(t)-ε(t-2)]=e -tε(t)-e -2 e -(t-2)ε(t-2)则其象函数为2.已知下列象函数F(s)，求原函数f(t)。

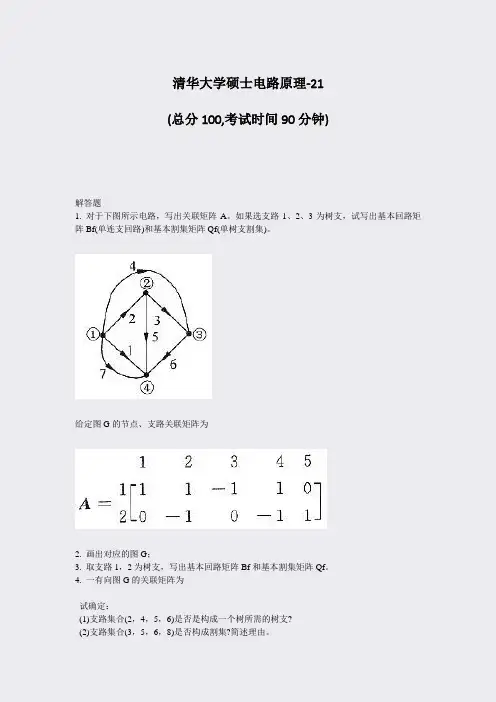
清华大学硕士电路原理-21(总分100,考试时间90分钟)解答题1. 对于下图所示电路，写出关联矩阵A。

如果选支路1、2、3为树支，试写出基本回路矩阵Bf(单连支回路)和基本割集矩阵Qf(单树支割集)。

给定图G的节点、支路关联矩阵为2. 画出对应的图G；3. 取支路1，2为树支，写出基本回路矩阵Bf和基本割集矩阵Qf。

4. 一有向图G的关联矩阵为试确定：(1)支路集合(2，4，5，6)是否是构成一个树所需的树支?(2)支路集合(3，5，6，8)是否构成割集?简述理由。

电路如下图(a)所示，图(b)为其对应的拓扑图，标准支路定义为图(c)所示形式。

(a)(b)(c)5. 试写出该电路矩阵形式的节点电压方程中的各矩阵或向量6. 以图(b)中支路1，2，3为树支，写出图(b)的基本回路矩阵Bf和基本割集矩阵Qf。

下图(a)为一电路的有向图。

(a)7. 试以1，3，5为树支分别写出基本回路矩阵Bf和基本割集矩阵Qf(支路排列顺序为1，3，5，2，4)；8. 试写出图(b)所示电路的状态方程，并整理成标准形式(b)9. 列写下图所示电路的状态方程。

10. 以uC、iL为状态变量列出下图所示电路的状态方程，并整理成标准形式=AX+BV，其中X=[uC iL]T，V=[uS iS]T。

11. 电路如下图所示。

以iL1、iL2、uC1、uC2为状态变量，写出该电路的矩阵形式的状态方程。

12. 选择电容电压uC和电感电流iL为状态变量，列写下图电路的状态方程(不必求解)。

13. 试列写下图电路的状态方程，并整理成标准形式，其中X=[uC1uC2iL]]T。

14. 电路如下图所示。

(1)以1、2、3支路为树支写出关联矩阵A、基本回路矩阵Bf和基本割集矩阵Qf；(2)列写以uC、iL为状态变量的状态方程，并整理成标准形式。

15. 列写下图所示电路的状态方程，并整理成标准形式，其中X=[uC3iL4iL5]T。

16. 列写下图电路矩阵形式的状态方程，其中X=[uC1uC2iL]T。

清华大学硕士电路原理-1(总分：100.00，做题时间：90分钟)一、解答题(总题数：13，分数：100.00)1.求下图所示电路中1.4V电压源发出的功率P 1和0.5A电流源发出的功率P 2。

（分数：7.00）__________________________________________________________________________________________ 正确答案：()解析：解设电压源中的电流和电流源两端的电压参考方向如下图所示。

由图可得，U=1.4V则1.4V电压源发出的功率为P 1=1.4×(-0.3)=-0.42W0.5A电流源发出的功率为P 2=1.4×0.5=0.7W电路如下图所示，求：（分数：14.00）(1).a，b两点间开路电压U ab（分数：7.00）__________________________________________________________________________________________ 正确答案：()解析：解当a，b两端开路时，由KCL有I+3I=1，解得I=0.25A。

由此可得开路电压U ab =-6I+2=-0.25×6+2=0.5V(2).a，b两点间短路电流I ab（分数：7.00）__________________________________________________________________________________________ 正确答案：()解析：解设短路电流方向如下图所示。

由KCL有I+3I=1+I ab则由KVL有6I=2，即解得。

2.求下图所示电路中的电流I x。

（分数：7.00）__________________________________________________________________________________________ 正确答案：()解析：解由KCL及KVL，有5I x +(2+I x)×3+4I x =12解得I x =0.5A。

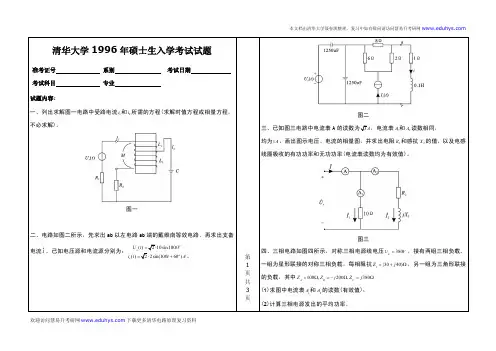
图一二、电路如图二所示，先求出ab 以左电路ab 端的戴维南等效电路，再求出支备。

已知电压源和电流源分别为：o()210sin100()22sin(10060s s U t tV i t t 图二三、已知图三电路中电流表A 的读数为3A ，电流表1A 和2A 读数相同，，画出图示电压、电流的相量图，并求出电阻2R 和感抗X 线圈吸收的有功功率和无功功率(电流表读数均为有效值)。

图三四、三相电路如图四所示，对称三相电源线电压380L U V ，接有两组三相负载。

一组为星形联接的对称三相负载，每相阻抗1(3040)Z j ，另一组为三角形联接,200,380B C Z j Z j 2A 的读数(有效值)；(2)计算三相电源发出的平均功率。

图五六、图六中方框部分为一由线性电阻组成的对称二端口网络。

若现在和直流电压源。

测得2-2端口的开路电压为7.2V ，短路电流为的传输参数T1-1’处接一直流电流源，在端口2-2’接电阻网络（图，则电流源Is 应为多少?图六七，已知图七电路在0t 时，已达稳态(其中开关12,K K 闭合，开关当0t 时，四个开关同时动作(即开关12,K K 断开，开关12,K K 闭合)。

求开关动作后，经过多少时间电流()U t 到达零伏。

图七八电路的状态方程。

(整理成标准形[][][][x A x B U图八九、用运算法(拉普拉斯变换法)求图九电路中电容电压()U t，0t 。

已知:00()20100stU t tt,(0)2,()1L ci A U t V图九十、图十所示电路为一由电阻组成的无源网络R。

用不同的输入电压1U及负载电阻2R也进行实验，测得数据为：(图a电路)当124,1U V R时，122,1I A U V当126,2U V R时，1 2.7I A今保持16U V，网络R不变，去掉电阻2R，改接电容C，该电容原来充电，电容为 10uF (图b电路)。

当0t 时闭合开关K，求电容()?cU t图a第3页共3页图b图一端戴维南等效电路：电阻，求其功率P。

清华大学硕士电路原理-2(总分：100.00，做题时间：90分钟)一、解答题(总题数：13，分数：100.00)1.求下图所示电路中流过电阻R的电流I。

（分数：4.00）__________________________________________________________________________________________ 正确答案：()解析：解将题干图中受控电流源转换成受控电压源(下图所示电路)。

解法1：回路法(电阻单位为kΩ，电流单位为mA，电压单位为V)设回路电流如上图所示，则回路电流方程为解得I 3 =-2.45mA，则流过电阻R的电流I=-I 3 =2.45mA。

解法2：节点法选参考节点如上图(a)所示，节点电压方程为以上3式联立求解，得U 2 =7.36V，则。

2.电路如下图所示。

求图中1A电流源两端的电压U。

（分数：8.00）__________________________________________________________________________________________ 正确答案：()解析：解按叠加定理将原电路分解为2个电路，如下图(a)和图(b)所示。

图(a)图(b)由图(a)得U"=-(3+2∥2)×1=-4V由图(b)得则U=U"+U"=-2V3.下图所示电路方框内是不含有独立电源的线性电阻网络。

aa"接直流电压U 1，bb"接直流电压U 2，cc"两端的开路电压为U 3。

已知U 1 =2V、U 2 =3V时，U 3 =1V；U 1 =3V、U 2 =2V时，U 3 =2V。

当U 1 = 10 V、U 2 =10V时，U 3应是多少?（分数：8.00）__________________________________________________________________________________________ 正确答案：()解析：解由叠加定理，可设U 3 =K 1 U 1 +K 2 U 2，代入已知条件有解得。