七年级数学角的度量1
- 格式:pdf
- 大小:1.72 MB
- 文档页数:10




七年级数学角的度量知识点角度是我们在日常生活中接触到的一个最基本的概念,我们可以用角度来描述我们身边的很多物理现象。
在七年级数学中,学习角的度量是一项十分重要的任务。
下面本文将为大家介绍七年级数学角的度量知识点。
1. 角的概念在平面内,由两条线段共同确定的图形部分称为角,其中两条线段称为角的两边,它们的公共端点称为角的顶点。
一个角被度量为它所对应弧长的一个单位。
2. 角的度量单位我们平常用的角的度量单位是度。
一个角度有360个度,一个直角度量为90度,一个平角度量为180度。
此外,还有一种度量角的方法称为弧度制。
一个圆的周长被定义为2π弧度,因此一个角度量为θ度等于θ/180π个弧度。
3. 角度制与弧度制间的转换角度制与弧度制是两种不同的角的度量方法。
有时候需要在两者之间进行转换。
具体的转换公式是:弧度制转角度制的公式:θ(角度)=180π×弧度角度制转弧度制的公式:θ(弧度)=θ(角度)π/1804. 角的分类根据角度的大小,我们可以将角分为三类:锐角、直角、和钝角。
锐角:大于0度、小于90度的角被称为锐角。
直角:度量为90度的角被称为直角。
钝角:大于90度、小于180度的角被称为钝角。
5. 角的性质下面是角的主要性质:相邻角:具有公共边和公共顶点的两个角被称为相邻角,它们之间的度数相加等于180度。
对顶角:由两对相交的直线所形成的4个角中,相对位置的两个角被称为对顶角。
对顶角度数相等。
同旁内角:两条平行线被直线所截成的四个内角中,同侧相对的两个内角被称为同旁内角,它们之间的度数相等。
6. 角的常见误区在学习角的度量时,有一些常见的误区需要注意:将角度制和弧度制的概念混淆。
度数和弧度之间的转换运算错误。
7. 总结角度的概念和性质是数学中一项重要的知识点。
在学习角度的度量过程中,我们需要掌握角的分类、度量单位以及角度制和弧度制的转换方法。
同时,还要注意一些常见的误区。
通过认真学习和思考,我们相信大家可以熟练掌握角度的度量知识点,并能够运用到实际问题的解决中。

角角:由一点引出两条射线形成的图形叫做角。
这两条射线叫做角的。
这一点叫做角的。
角也可看作是由一条射线绕它端点旋转而成的。
角的表示方法:(1)用三个大写英文字母表示;(2)用一个大写英文字母表示;(3)用阿拉伯数字表示;(4)用小写希腊字母表示。
角的度量单位:1度记作1º,1分记作1¹,1秒记作1¹¹.角的表示方法:①用三个大写字母表示:如∠AOB②用一个大写字母表示:如∠O(只适用单独一个角)③用弧线加数字来表示: 如∠1④用弧线加希腊字母来表示:如∠a角的度量单位的换算:1° = 1′ = 1周角= 1平角=平角的一半叫做直角;小于直角的角叫做锐角;大于直角而小于平角的角叫做钝角.它们之间的关系是:1周角=2平角=4直角=360º1平角=2直角=180º 1直角=90º换算方法:(1)把高级单位转化为低级单位要乘进率;(2)把低级单位转化成高级单位要除以进率;(3)转化时必须逐级进行,越级转化容易出错。
角的平分线:余角和补角:余角:两个角的和等于90°(直角),就说这两个角互为余角,简称互余,即其中一个角是另一个角的余角。
补角:两个角的和等于180°(平角),就说这两个角互为补角,简称互补,即其中一个角是另一个的补角。
余角和补角的性质1、同角或等角的余角相等。
2、同角或等角的补角相等。
例1、把一个周角7等分,每一份是多少(精确到分)例2、19°36′= °56°37′= °38°15′和38.5°一样大吗?例3、⑴150°20′25″+ 11°39′35″⑵90°21′16″-26°10′6″⑶12°5′×6⑷16°18′÷3例4、如图:AOB是一条直线,∠AOC=900,∠D OE=900,写出∠AOD、∠C OD、∠AOC、∠AOB、∠B OD中某些角之间的两个等量关系。

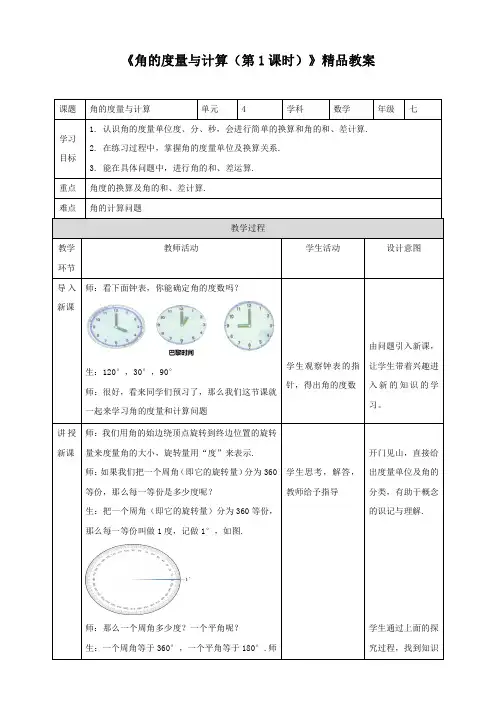
《角的度量与计算(第1课时)》精品教案生:120°,30°,90°师:很好,看来同学们预习了,那么我们这节课就一起来学习角的度量和计算问题师:那么一个周角多少度?一个平角呢?生:一个周角等于360°,一个平角等于:谁能告诉我还有什么角?生:平角的一半(即90°的角)叫做直角.生:小于直角(即小于90°)的角叫做锐角.生:大于直角但小于平角(即大于90°但小于180°)的角叫做钝角.师:恩,很好,那么我们怎样表示角的度数呢?上节课我们学了可以用量角器来度量,是吧,可是我们量出的角就一定是整数吗?生:我觉得不会,有可能不是整度数师:所以需要考虑用更小的单位来度量.那么有哪些比度还小的量呢?下面我来告诉大家:课件展示:1°的为1分,记作“1′”,即1°=60′.1′的为1秒,记作“1″”,即1′=60″.师:谁能更简洁的描述一下?生:1°=60′,1′=60″,1′=(160)°,1″=(160)'师:度、分、秒是角的基本度量单位.度、分、秒之间的换算是60进制,这与时间的时、分、秒之间的换算是一样的.课件展示:例1用度、分、秒表示54.26°.练习:0.25°等于多少分?等于多少秒?例2用度表示48°25′48″.学生思考,解答,教师给予指导的共性,充分发挥学习的主动性,同时也培养了学生分析问题的能力。
通过问题提出探讨的目标,解决角度加减计算的难点.练习:把下列各题结果化成度(1)72°36′(2)37°14′24″师:通过例题与练习,能不能总结一下角的度数的换算规律呢?生:把度化成度、分、秒的形式,即从高单位向低单位转化时,一般都是把度的小数部分化成分,把分的小数部分化成秒,每级变化乘以60生:把度、分、秒化成度的形式,即从低单位向高单位转化时,一般都是先把秒分化成分,再把分化成度,每级变化除以60课件展示:例3计算:(1)37°28′+24°35′;(2)83°20′-45°38′20″.练习;计算:(1)72°12′+50°40′30″;(2)113°50′40″-57°48′42″.师:我们再来总结一下角度数的运算生:进行加法运算时,先算秒,再算分,最后算度,够60″时,把60″化为1′,够60′时,把60′化为1°生:进行减法运算时,不够减,借1°化为60′,借1′化为60″课件展示:例4、21°31′27″×3师:把度、分、秒分别乘以乘数,满60,向前一位进1.例5、(1)63°21′39″÷3(2)106°6′25″÷5师:从“度”开始除,得数就是“度”值,把余数乘以60加到“分”里;再用“分”除,得数就是“分”值,把余数乘以60加到“秒”里;最后用“秒”除,得数4舍5入一下就是“秒”值.简单学生思考回答,试着解答例题及练习,同时也总结出一些关于角度数计算的规律.多角度的例题设计,加深学生对概念与换算关系的理解.知识的拓展与提升提高应考能力,全面提高学生分析、解决问题的能力.说就是把度的余数化成分,把分的余数化成秒后再除.课堂练习1.从3时到6时,钟表的时针旋转角的度数是().A.30°B.60°C.90°D.120°答案:C2.将31.39°化成度分秒表示,结果是()A.31°3′9″B.31°23′4″C.31°23′24″D.31°23′答案:C3.若∠1=5.2°,∠2=312′,∠3=1872″,则下列说法正确的是()A.∠1=∠2B.∠2=∠3C.∠1=∠3D.∠1,∠2,∠3互不相等答案:A4.33°52′+21°54′=_____°_____′.答案:55,465.计算:(1)51°37′42″+29°58′53″;(2)75°28′33″-60°38′49″;(3)36°54′+143°6′;(4)90°-25°41′39″.答案:解:(1)原式=81°36′35″.(2)原式=14°49′44″.(3)原式=180°.(4)原式=64°18′21″.拓展提高景欣在周六下午六点多钟外出买东西时,看手表上学生自主解答,教师讲解答案。




求⾓的度量度分秒的计算及习题七年级数学求⾓的度量度分秒的计算及习题第三节⾓(⼆)⾓的度量与画法⼀. 教学内容:⾓的度量与画法【知识点讲解】1. ⾓的度量:按对线、对中、度数的步骤⽤量⾓器量出⾓的度数2. ⾓的度数计算:⾓的单位是度分秒,都是60进制,可以⽐照时间中的时分秒理解,分别⽤“°”、“ ’”、“ ””来表⽰。
3 . 余⾓、补⾓的概念与性质:如果两个⾓的和是90度(或直⾓)时,叫做两个⾓互余;4. 如果两个⾓的和是180度(或平⾓)时,叫做两个⾓互补。
(补⾓同理)性质:同⾓(或等⾓)的余⾓相等;同⾓(或等⾓)的补⾓相等(补⾓同理)5. 能利⽤三⾓板画出15°、30°、45°、60°、75°、90°等11种特殊⾓6. 会⽤尺规画⼀个⾓等于已知⾓,⾓的和、差的画法。
【技能要求】1. 掌握度、分、秒的计算。
2. 逐步掌握学过的⼏何图形的表⽰⽅法,懂得学过的⼏何语句,能由这些语句准确、整洁地画出图形。
认识学过的图形,会⽤语句描述这些简单的⼏何图形。
【典型例题】例1. 将33.72°⽤度、分、秒表⽰。
解:33.72°=33°+(0.72×60′)=33°+43.2′=33°+43′+(0.2′×60″)=33°43′12″例2. ⽤度表⽰152°13′30″。
解:152°13′30″=152°+(13 )′=152°+13.5′=152°+( )°=152.225°例3. 判断下列计算的对错,对的画“√”,错的说明错在哪⾥,并改正。
(1)31°56′÷3=10°52′(2)138°29′+44°49′=183°18′(3) 13.5°×3=39.50(4) 21.36°-18°30′=3.14°.解:(1)错,因为⽤1°=100′计算的。
七年级角知识点在数学领域中,角是一个重要的知识点,尤其是在初中数学中,学习角的相关知识是必不可少的。
在七年级,我们需要掌握的角的基础知识有:角的定义、角的度量和角的分类等方面。
一、角的定义角是由两条射线所夹的一部分平面区域。
其中,这两条射线称为角的两条边,它们共同的起点称为角的顶点。
如下图所示,∠ABC就是一个角,其中AB和BC是两条边,B是角的顶点。
二、角的度量度是衡量角大小的基本单位,一个完整的角是360度。
对于任意一个角,我们可以用度数来度量它的大小。
下面是一些常见的角度数:直角:90°;钝角:大于90°,小于180°;锐角:小于90°。
除了用度数来度量角的大小外,我们还可以用弧度来度量角的大小。
弧度是指角所对应的圆弧长度等于半径长的一部分。
例如,半径为1的圆的弧长等于π,那么这个圆的角度数就是180°,弧度数就是π。
三、角的分类在数学中,我们可以根据角的大小和特性来分类。
下面介绍一下角的分类:1.锐角、直角和钝角角可以分为锐角、直角和钝角三类。
其中,锐角是指角度小于90度,直角是指角度等于90度,钝角是指角度大于90度而小于180度。
如下图所示,∠A、∠B、∠C分别是锐角、直角和钝角。
2.对顶角和邻补角对顶角是指两个角的顶点在一条直线上,并且两个角的非公共边互相垂直。
如下图所示,∠1和∠2是一对对顶角,∠3和∠4是一对对顶角。
邻补角是指两个角的和等于90度。
如下图所示,∠A和∠B、∠C和∠D是一对邻补角,它们的和分别为90度。
3.互补角和补角互补角是指两个角的和等于180度。
如下图所示,∠A和∠B、∠C和∠D是一对互补角,它们的和分别为180度。
补角是指两个角的和等于一个直角的角度(90度)。
如下图所示,∠A和∠B、∠C和∠D是一对补角,它们的和分别为90度。
总结角是初中数学中的一个重要知识点,它涉及到角的概念、角的度量和角的分类等方面。