当前位置：文档之家 › 动态电路地时域分析报告

动态电路地时域分析报告

  • 格式：doc
  • 大小：901.73 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

《电路分析》——动态电路时域分析

《电路分析》——动态电路时域分析
iL(0+)= iL(0－) 则电感电流（磁链）换路前后保持不变。
注意:
（1）电容电流和电感电压为有限值是换路定律成立的条件。 （2）换路定律反映了能量不能跃变。
《电路分析》——动态电路时域分 析
LC
L iL(0)
+
C uC(0)
-
LC
(a) 稳态时 的L和C
(b) 换路前有储能 的L和C
(c) 换路前无 储能的L和C
第5章 动态电路的时域分析
重点
1. 动态电路方程的建立及初始条件的确定； 2. 一阶电路的零输入响应、零状态响应和
全响应求解； 3. 稳态分量、暂态分量求解； 4. 一阶电路的阶跃响应和冲激响应。
《电路分析》——动态电路时域分 析
由电源和电阻器构成的电阻性网络，是用代 数方程来描述的，求解过程不涉及微分方程。
0
t
零输入响应
《电路分析》——动态电路时域分 析
5.3.2 一阶RC电路的零输入响应
换路后外加激励为零，仅由动态元件初始储能所 产生的电压和电流。
已知 uC (0－)=U0 ; uS =0
t
uc (t) U0e RC t 0
ic (t)
U0 R
e
t RC
t0
《电路分析》——动态电路时域分
a1
df (t) dt
a0
f
(t)
e(t)
t0
(3)高阶电路
电路中有多个动态元件，描述电路 的方程是高阶微分方程。
an
d
n f (t) dt n
an1
d
n1 f (t) dt n1
a1
df (t) dt
a0
f
(t)

动态电路的时域分析共115页文档

动态电路的时域分析共115页文档
动Байду номын сангаас电路的时域分析
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ；权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊，可是金 子可以 拉着它 的鼻子 走。— —莎士 比
41、学问是异常珍贵的东西，从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联

动态电路的时域分析-精品文档

动态电路的时域分析-精品文档

10-1 一阶电路 10-1-1 一阶电路的零输入响应 3、一阶电路零输入响应概述 （3）时间常数τ • 表征零输入响应衰减的快慢程度
2
uC(0+)= uC(0–)=10V
2i
+
ic 4 i
0.5F
+
-
-
uc
10-1 一阶电路 10-1-1 一阶电路的零输入响应 解：以uC为变量的方程 duC 0.5 dt + 0.25uC+ 0.5uC=i duC dt + uC= 0
2i
2
+
ic
i 4 i ic 0.5F
+
-
-
uc
uC(0+)=10
iR
R
-
uC(0)=U0 U0 U0 R 0 U0 R
U0 - RC e = - iC iR= R （ t 0） R(0,
2 )=0.5CU 0
t
uC iC
iR t
10-1 一阶电路 10-1-1 一阶电路的零输入响应 例1 图示电路原处于 稳态，t=0时将开 关接到“2”，对t0 求uC。 uC(0–)=186/9=12V
duC 1 1 1 – uR+( 40 + 100 )uC+ 4dt =0 40 duR 2 u =0 dt + 25 R
（t0） （t0）
10-1-1 一阶电路的零输入响应 2、RL电路
1 2
iL L R
iL=I0e -
R
L t
（t0）
R
L t
I0
R1 iL(0-)=I0
u= -RI0
e-
iL(0+)=iL(0–)=6A 解：以iL为变量的方程 diL diL +80.5iL+0.5(– ) =0 dt dt diL dt +8iL =0 （t0） 以u为变量的方程

电路分析基础第4章 动态电路的时域分析

电路分析基础第4章 动态电路的时域分析
图4.2-4 例4.2-2用图(一)
第4章 动态电路的时域分析 解 (1) 先计算电容电压uC(0－)和电感电流iL(0－)。开关
开启前电路已处于直流稳定状态，这时电容相当于开路，电 感相当于短路，t=0－时的等效电路如图4.2-5(a)所示。由图(a) 可得
图4.2-5 例4.2-2用图(二)
第4章 动态电路的时域分析
第4章 动态电路的时域分析
(2) 根据换路定律，有
iL(0+)=iL(0－)=1 A (3) 画出换路后瞬间t=0+时的等效电路，计算其他支路 电压、电流的初始值。根据置换定理，用一个电流值等于
iL(0+)=1 A的理想电流源代替电感元件，画出t=0+时的等效电 路如图(b)所示。对图(b)中右边一个回路应用KVL，得
第4章 动态电路的时域分析 图4.2-1 动态电路过渡过程说明用图
第4章 动态电路的时域分析
4.2.2 换路定律 如果电容电流iC和电感电压uL在无穷小区间［t0－，t0+］
为有限值，则上面两式中等号右边第二项积分为零，于是有
uC (t0 iL (t0
) uC (t0 ) iL (t0 )
4.2.1 动态电路的过渡过程 当动态电路的结构或元件参数发生变化时，电路将从一
个稳定状态变化到另一个稳定状态，这种变化一般需要经历 一个过程，这个过程称为过渡过程。通常把电路中电源的接 入或断开，以及元件参数或电路结构的突然改变，统称为 “换路”。下面以图4.2-1(a)所示的动态电路为例来说明过 渡过程的概念。
第4章 动态电路的时域分析
4.1 电容元件和电感元件
4.1.1 电容元件 1. 电容元件的定义 电容元件是从实际电容器中抽象出来的理想化模型。实

动态电路的实验报告

动态电路的实验报告

一、实验目的1. 理解动态电路的基本原理和特性。

2. 掌握动态电路的时域分析方法。

3. 学习使用示波器、信号发生器等实验仪器进行动态电路实验。

4. 通过实验验证动态电路理论，加深对电路原理的理解。

二、实验原理动态电路是指电路中含有电容或电感的电路。

动态电路的特点是电路中的电压、电流随时间变化，其响应具有延时特性。

本实验主要研究RC一阶动态电路的响应。

RC一阶动态电路的零输入响应和零状态响应分别由电路的初始状态和外加激励决定。

零输入响应是指在电路没有外加激励的情况下，由电路的初始状态引起的响应。

零状态响应是指在电路初始状态为零的情况下，由外加激励引起的响应。

三、实验仪器与设备1. 示波器：用于观察电压、电流随时间的变化。

2. 信号发生器：用于产生方波、正弦波等信号。

3. 电阻：用于构成RC电路。

4. 电容：用于构成RC电路。

5. 电源：提供实验所需的电压。

6. 导线：用于连接电路元件。

四、实验步骤1. 构建RC一阶动态电路，连接好实验仪器。

2. 设置信号发生器，输出方波信号，频率为1kHz，幅度为5V。

3. 使用示波器分别观察电容电压uc和电阻电压ur的波形。

4. 改变电路中的电阻R和电容C的值，观察电路响应的变化。

5. 记录实验数据，分析实验结果。

五、实验结果与分析1. 当电阻R和电容C的值确定后，电路的零输入响应和零状态响应分别如图1和图2所示。

图1 零输入响应图2 零状态响应从图中可以看出，零输入响应和零状态响应均呈指数规律变化。

在t=0时刻，电容电压uc和电阻电压ur均为0。

随着时间的推移，电容电压uc逐渐上升，电阻电压ur逐渐下降，最终趋于稳定。

2. 当改变电阻R和电容C的值时，电路的响应特性发生变化。

当电阻R增大或电容C减小时，电路的响应时间延长，即电路的过渡过程变慢；当电阻R减小或电容C增大时，电路的响应时间缩短，即电路的过渡过程变快。

3. 通过实验验证了动态电路理论，加深了对电路原理的理解。

电路分析基础实验四：动态电路的时域仿真实验报告

电路分析基础实验四：动态电路的时域仿真实验报告

电路分析基础实验四：动态电路的时域仿真实验报告实验四：动态电路的时域仿真一.实验内容及要求1．使用Multisim仿真测试动态电路中常用的换路元件功能。

2．利用Multisim仿真分析动态电路。

二.实验要求1．掌握动态电路的工作原理和常用的换路元件功能。

2．掌握Multisim仿真分析动态电路的方法。

三.实验设备PC机、Multisim软件四.实验步骤1．使用Multisim编辑动态电路中的储能元件和换路元件：从元器件库中选择储能元件电容和电感，设置储能元件的参数；从元器件库中选择常用的换路元件，包括单刀单掷开关、单刀双掷开关、电流控制开关、电压控制开关、时间延迟开关，设置换路元件的参数。

（1）储能元件电容和电感的添加（2）放置开关1）单刀单掷开关2）单刀双掷开关3）电流控制开关4）电压控制开关5）时间延迟开关2．仿真测试时间延迟开关的功能：用Multisim绘制电路原理图1，使用菜单栏中的Simulate→Analyses→Transi ent analysis命令进行仿真，设置Starttime(TSTART)=0s和End time(TSTOP)=0.005s，观察并记录V(2)的变化曲线。

图1延迟开关功能测试仿真电路原理图（1）绘制电路原理图1如下：（2）设置Start time(TSTART)=0s和End time(TSTOP)=0.005s，观察并记录V(2)的变化曲线如下：3．仿真测试电压控制单刀双掷开关的功能：用Multisim 绘制电路原理图2，打开示波器，设置参数Timebase→Scale=50ms/Div，使用菜单栏中的Simulate→Run 命令进行仿真，使用菜单栏中的Simulate→Stop命令停止仿真，观察并记录示波器显示的信号波形。

图2电压控制单刀双掷开关功能测试仿真电路原理图（1）绘制电路原理图2如下图：（2）示波器设置参数XXX→Scale=50ms/Div，使用菜单栏中的Simulate→Run命令进行仿真，使用菜单栏中的Simulate→Stop命令停止仿真，观察并记录示波器显示的信号波形下图：4．动态电路的时域仿真：用Multisim绘制电路原理图3，使用菜单栏中的Simulate→Analyses→Transientanalysis命令进行仿真，设置Starttime(TSTART)=0s和Endtime(TSTOP)=0.01s，观察并记录V(3)的变化曲线；设置电容初值电压为5V，设置Transient analysis→XXX→User defined，进行仿真分析，观察并记录V(3)的变化曲线。

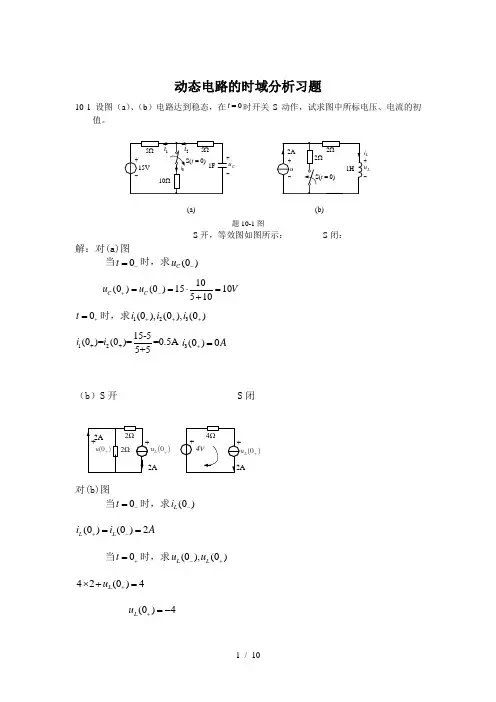
动态电路的时域分析报告

动态电路的时域分析报告

动态电路的时域分析习题10-1 设图（a ）、（b ）电路达到稳态，在0=t 时开关S 动作，试求图中所标电压、电流的初值。

C u L i L(a) (b)题10-1图S 开，等效图如图所示： S 闭：解：对(a)图当0t -=时，求(0)C u -10(0)(0)1510510C C u u V +-==⋅=+0t +=时，求123(0),(0),(0)i i i +++1+2+15-5(0)=(0)==0.5A 5+5i i 3(0)0i A +=（b ）S 开 S 闭+_(0)u (0)L u (0)L对(b)图当0t -=时，求(0)L i -(0)(0)2L L i i A +-==当0t +=时，求(0),(0)L L u u -+42(0)4L u +⨯+=(0)4L u +=-(0)2240u +=⨯-=10-2电路如图所示，已知Ω==421R R ，Ω=23R ，H L 1=，V U S 121=，V U S 62=。

电路原来处于稳定状态，0=t 时，开关S 闭合，试求)0(+L i 和)0(+L u 。

题10-2 图 题10-2 图解：S 开S 闭当0t -=时，求(0)L i -223(0)(0)1S L L U i i A R R +-===+当0t +=时，求(0)L u +111813421253246(0)10(0)3L L i i i i i i i u u ++⎧⎫=⎪⎪=+⎧⎫⎪⎪⎨⎬⎨⎬+=⎩⎭⎪⎪=⎪⎪⎩⎭+=+=10-3 设图示电路达到稳态，在0t =时开关S 动作，试求(0)c u +、(0)L i +、(0)i +、dtdu C /)0(+和(0)L di dt +。

(a)(b)解：当0t -=时，求(0),(0)c L u i --，等效电路如图（a ）15(0)(0).(60//20)530(60//20)C C u u V +-===+_1560(0)(0).0.2530(60//20)6020L L i i A +===++当0t +=时，求(0),(0)L c u i ++,等效电路如图（b ）(0)5200.250L u V +=-⨯=S U -+2S L15101(0)0.253010c i A +-=-=(0)(0)1/6C C du i V s dt C ++==(0)(0)0A/s L L di u dt L++==10-4设图示电路达到稳态，在0t =时开关S 动作，试求(0)c u +、(0)L i +、(0)R u +、(0)c du dt +和(0)L di dt +。

电路分析基础第二篇动态电路的时域分析标准版文档

电路分析基础第二篇动态电路的时域分析标准版文档

2、若u(t)=常数（直流），则电压的变化率为零，即电容两 端有电压而无电流，故电容C相当于开路,即电容有隔直流的 作用。 直流开路性。
3、电容电压变化越快，电流越大。
三、电容电压的性质：记忆性和连续性
i(t) c du(t) dt
C i
u(t) 1
t
i(t)dt
C
+u-
初始值
1 t0i(t)dt1 t i(t)dt
四、电感的等效电路 有电流(己充电)的电感＝无电流(未充电)的电感并电流源
iL(t)
iL(t0)
1 L
t
t0 uL(t)dt
iL(t0)i1(t) I0 i1(t) t t0
一个具有初始电流的电感，若已知 iL(t0)=I0，则在 t t0 时 可等效为一个初始电流为零的电感与电流源相并联的电路，电
四、电容的等效电路：已充电电容＝未充电电容串电压源
uc(t) uc(t0)C 1
t
i(t)dt
t0
uc(t0)u1(t) U0 u1(t) t t0
一个已被充电的电容，若已知 u(t0)=U0，则在 t t0 时可
等效为一个未充电的电容与电压源相串联的电路，电压源的
电压值即为t0时电容两端的电压U0。 i(t)
二、电容元件的电压电流关系
2、若u(t)=常数（直流），则电压的变化率为零，即电容两端有电压而无电流，故电容C相当于开路,即电容有隔直流的作用。
1H电感通以图(b)所示的电流。
动态电路：含动态元件电的解电电路。容器
瓷质电容器
定在义t ≥：t0一组时最电少路的中变的量任，何若电已路知变它量们，在这样t0的时电的路数变值量称为电路固的状定态变电量。容 器（初始状态），则连同所有在

动态电路时域分析-精品

动态电路时域分析-精品

RL电路
根据KCL列出电流方程为
iR(t)iL(t)is(t)
由于 iR uL , R
u
L
L
diL dt
§4.2 动态电路的方程
t=0
iL
iR
+
R
L uL
is
–
RL并联电路
diL RiLRis dt L L
一阶电路: 只含有一个动态元件的电路， 描述电路的方程是一阶线性微分方程。
第4章 动态电路时域分析
电容元件 VCR的积
分形式
某一时刻的电容电压值与- 到该时刻的所有电流
值有关，即电容元件有记忆电流的作用，故称电 容元件为记忆元件。
研究某一初始时刻t0 以后的电容电压，需要知道t0 时刻开始作用的电流 i 和t0时刻的电压 u（t0）。
第4章 动态电路时域分析
§4.1 动态电路元件
8．电容元件的功率及能量
iL(t)iL(0)L0 u( )d
其中
1 iL(0)L
0uL()d
称为电感电流的初始值。
电感元件VCR 的积分关系
第4章 动态电路时域分析
§4.1 动态电路元件
i(t)1 t u()d L
1 t
iL(t)iL(t0)Lt0
u()d
某一时刻的电感电流值与-∞到该时刻的所有 电压值有关，即电感元件有记忆电压的作用， 电感元件也是记忆元件。
实际电路中电感的电压 u为有限值，则电感电流 i 不能跃 变，必定是时间的连续函数。
第4章 动态电路时域分析
§4.1 动态电路元件
在已知电感电压uL(t)的条件下，其电流iL(t)为
iL(t)
1 L
tuL()d

电路基础与实践 第4版 第3章 动态电路的时域分析

电路基础与实践 第4版 第3章 动态电路的时域分析
3.1.2 电容元件
第3章动态电路的时域分析
1.线性电容
i
线性电容极板上储存的电荷量和其端电压成正比：
q C
+
C
u
u－
C为电容量，单位：法拉（F）；常用单位：μF、pF
2.电容元件的电压电流关系（关联参考方向）
i dq C du dt dt
（电容元件的VCR）
u 1
t
i dt u(0)
开关闭合后：I=0,Uc=10V,新的 稳定状态
是否S闭合，UC就立即由0V升至10V呢
闭合前：
WC
1 CU 2 2
0
闭合后：
WC
1 CU 2 1 1102 50(J )
2
2
？
电路基础与实践
第3章动态电路的时域分析
闭合前：
WC
1 CU 2 2
0(J )
闭合后：
WC
1 CU 2 2
1 1102 2
1
t
i dt
C0
C0
u(0) — t = 0 时电压u的值，若u(0) = 0
电路基础与实践
3.电容元件储存的能量
第3章动态电路的时域分析
（关联参考方向）
电容 C 在任一瞬间吸收的功率：
p u i u C du P > 0 吸收能量 dt P < 0 释放能量
电容 C 在 dt 时间内吸收的能量：
3)熟练掌握三要素法求解一
析。 4)能够按照要求搭建动态电路，
阶电路。
会对电路进行测量、对测量数据
4)了解阶跃函数和阶跃响应。 进行分析处理，并形成报告。
2024年8月31日11时50分
5)会对动态电路进行仿真。

电路分析(第六版)动态电路的时域分析

电路分析(第六版)动态电路的时域分析
路后的iL(t)。
动态电路的时域分析
图7.14 题7.2 3图
动态电路的时域分析
图7.15 题7.2 4图
动态电路的时域分析
7.3 一阶电路的零状态响应
零状态响应是指当电路初始状态为零时,由外加激励产 生的响应。外加激励可为直流 电源(电压或电流),也可为交 流电源。
动态电路的时域分析
7.3.1 RC 电路的零状态响应 如图7.16所示RC 串联电路,开关S闭合前uC(0- )=0,t=0
动态电路的时域分析
图7.18 RL 电路的零状态响应
动态电路的时域分析 根据图7.18中S闭合后的电路,依 KVL,有
式(7－17)也是一常系数一阶线性非齐次微分方程,它的解同 样由其特解icp和相应的齐次 方程的通解ich组成,即
动态电路的时域分析
动态电路的时域分析
动态电路的时域分析
图7.19 RL 电路零状态响应曲线
动态电路的时域分析 例 7.1 图7.2(a)所 示 电 路 中,已 知 US =18 V,R1 =1Ω,R2
=2Ω,R3 =3Ω, L=0.5H,C=4.7μF,t=0时,S闭合,设S闭合前电路已 处稳态。求i1(0+ )、i2(0+ )、 i3(0+ )、uL(0+ )、uC(0+ )。
图 7.2 例 7.1 图
L 相当于短路,此时电感电流 为iL(0- )=US/RS=Io。开关动作后
的初始时刻t=0+ 时,根据换路定律,有iL(0+ )=Io。
这时电感中的初始储能
将逐渐被电阻消耗直至殆
尽,电流为零,电感的消磁过程 便结束。下面通过数学分析,找
出电感电流和电压的变化规律。

动态电路的时域分析

动态电路的时域分析

动态电路的时域分析 第一节 换路及其初始条件一、电路的两种工作状态（稳态、动态） 1、稳态电路： （1）定义当电路在直流电源的作用下，各条支路的响应也是直流；当电路在正弦交流电源的作用下，各条支路的响应也是正弦交流，这种类型的电路称为稳态电路。

（2）特征：稳态电路中不存在换路现象，描述稳态电路的方程是代数方程。

2、动态电路： （1）定义当电路中含有储能元件或称动态元件（如电容或电感），电路中的开关在打开或闭合的过程中参数发生变化时，可使电路改变原来的工作状态，转变到另一个工作状态。

电路从一种稳态到达另一种稳态的中间过程称为动态过程或过渡过程。

过渡过程中的电路称为动态电路。

（2）待征：动态电路中存在动态元件且有换路现象，描述动态电路的方程是微分方程。

一阶电路：能够用一阶微分方程描述的电路； 二阶电路：能够用二阶微分方程描述的电路； n 阶电路：能够用n 阶微分方程描述的电路。

（3）存在原因：1）含有动态元件电感或电容 ::di L u L dtdu C i Cdt ⎧=⎪⎪⎨⎪=⎪⎩2）存在换路：电路结构或参数发生变化 二、换路 1、定义：电路中含有储能元件，且电路中开关的突然接通或断开、元件参数的变化、激励形式的改变等引起的电路变化统称为“换路”。

（1）换路是在0t =时刻进行的（2）换路前一瞬间定义为：0t -=；换路后一瞬间定义为：0t +=； （3）换路后达到新的稳态表示为：t =∞。

2、换路定律：在换路时电容电流和电感电压为有限值的条件下，换路前后瞬间电容电压和电感电流不能跃变。

即：(0)(0),(0)(0)c c L L u u i i +-+-==。

注意：00()()C C i t i t +-≠，00()()L L u t u t +-≠，00()()R R i t i t +-≠，00()()R R t u t +-≠ 三、独立初始条件 1、定义：一个动态电路的电容电压(0)C u +和电感电流(0)L i +称为独立初始条件，其余的称为非独立初始条件，非独立初始条件需通过已知的独立初始条件来求得。

动态电路时域分析-精品文档

动态电路时域分析-精品文档

12 R2 0.6H L
U 220 （2）确定i () i ( ) 18 . 3 A R 12 2 L 0 . 6 （3）确定时间常数 0 . 05 S R 12 2
第8章 动态电路的时域分析
[例] 图中，如在稳定状态下R1被短路，试问短路 后经过多少时间电流才达到15A？ R1 i
u ( 0 ) 2 V C u ( ) 4 V C 2 m s 500 t u 4 2 e V C
4
2 t (S) 0
第8章 动态电路的时域分析
[例] 图中，如在稳定状态下R1被短路，试问短路 后经过多少时间电流才达到15A？ R1 i
[解] 先应用三要素法求 8 + 电流i t =0 U （1）确定i (0+) – 220V U 220 i ( 0 ) 11 A R R 12 1 2 8
将电路中的独立源置零（电压源短路、电流 源开路),通过化简，最终可化为一个RC回路（或 者RL回路）的电路，是一阶电路，否则不是一阶 电路。
第8章 动态电路的时域分析
二、一阶பைடு நூலகம்路的解法通论（三要素法）
一阶电路的微分方程：例：P199 （a）（b）（c）（d 结论： 任何一个一阶线性电路，其数学模型是可以 整理成一个如下方程：
第8章 动态电路的时域分析
[例] 在下图中，已知U1=3V， U2=6V，R1=1k R2=2k，C= 3F ，t<0时电路已处于稳态。用三要 素法求t ≥ 0 时的 uC(t),并画出变化曲线。 1 S [解] 先确定uC(0+) 2 R1 uC()和时间常数 t = 0 + + + uC C t<0时电路已处于 U1– R2 U2 – – 稳态，意味着电容相 当于开路。 R U 2 1 u ( 0 ) u ( 0 ) 2 V C C R R 1 2 R U 2 2 u ( ) 4 V C R R 1 2

动态时域分析实验报告

动态时域分析实验报告

一、实验目的1. 掌握动态系统的时域分析方法。

2. 理解并应用拉普拉斯变换在动态系统分析中的作用。

3. 通过实验验证动态系统的时域响应特性。

二、实验原理动态系统时域分析是研究系统在时间域内对输入信号的响应特性。

通过对系统进行拉普拉斯变换，可以得到系统的传递函数，进而分析系统的稳定性、动态性能和频率特性。

三、实验仪器与设备1. 微机一台2. MATLAB软件3. 动态系统仿真软件四、实验内容1. 设计一个动态系统，其传递函数为G(s) = 1/(s+1)。

2. 利用拉普拉斯变换求出系统的零点、极点和自然频率。

3. 分析系统的稳定性，判断系统是否稳定。

4. 求解系统的单位阶跃响应、单位脉冲响应和单位斜坡响应。

5. 分析系统的动态性能，包括上升时间、峰值时间、调整时间等。

6. 通过实验验证动态系统的时域响应特性。

五、实验步骤1. 在MATLAB中，编写动态系统的传递函数G(s) = 1/(s+1)。

2. 利用MATLAB的拉普拉斯变换函数，求出系统的零点、极点和自然频率。

3. 利用MATLAB的step函数，绘制系统的单位阶跃响应曲线。

4. 利用MATLAB的impulse函数，绘制系统的单位脉冲响应曲线。

5. 利用MATLAB的step函数，绘制系统的单位斜坡响应曲线。

6. 分析系统的动态性能，包括上升时间、峰值时间和调整时间。

六、实验结果与分析1. 系统的零点、极点和自然频率如下：零点：无极点：-1自然频率：无2. 系统稳定性分析：由于系统只有一个极点，且位于左半平面，故系统是稳定的。

3. 单位阶跃响应曲线如图1所示：（此处插入单位阶跃响应曲线图）由图1可知，系统的上升时间为1秒，峰值时间为1.6秒，调整时间为2秒。

4. 单位脉冲响应曲线如图2所示：（此处插入单位脉冲响应曲线图）由图2可知，系统的脉冲响应为-1。

5. 单位斜坡响应曲线如图3所示：（此处插入单位斜坡响应曲线图）由图3可知，系统的斜坡响应为-1。

动态电路的时域分析

动态电路的时域分析

动态电路的时域分析
动态电路分析的基本方法是建立电路的微分方程，利用电路中的基尔
霍夫定律和伏安定律，推导出描述电路元件电压和电流变化关系的微分方程。

然后，通过求解微分方程，得到电路的时间响应，即电压和电流随时
间的变化规律。

动态电路的分析过程中需要考虑电路元件的动态特性，包括电容元件
和电感元件的存储能量和存储效应。

对于电容元件，其电压和电流之间的
关系可以用电容的充放电方程来描述。

而对于电感元件，其电压和电流之
间的关系可以用电感的变化率来描述。

在时域分析中，最常用的方法是Laplace变换法。

通过将电路中的微
分方程转化为复频域中的代数方程，可以大大简化电路的分析过程。

利用Laplace变换后的电路方程，可以通过进行代数运算和逆变换，得到电路
的时间响应。

动态电路的时域分析还需要考虑电路的初始条件。

对于包含存储元件
的电路，初始条件是指电容电压和电感电流在初始时刻的取值。

有时候，
电路的初始条件会影响电路的稳定性和响应速度，因此在进行时域分析时，需要充分考虑初始条件的影响。

此外，动态电路的时域分析还可以通过脉冲响应法进行。

该方法利用
电路的单位阶跃响应和冲击响应的线性叠加原理，可以将任意输入信号分
解为一系列单位阶跃函数和冲击函数，并通过对各个分量的处理来得到电
路的时间响应。

总之，动态电路的时域分析是电路理论中的重要内容。

通过对电路中各个元件的电压和电流随时间的变化进行分析，可以揭示电路的动态行为和响应过程，为电路设计和故障诊断提供重要的理论依据。

秋电路理论动态电路的时域分析

秋电路理论动态电路的时域分析
记忆特性：上式表明，线性非时变电容元件在t时刻的电 压值取决于从 –∞ 到t时刻的电流值。即电容
电压u与电容元件的电流i历史有关;电容元件具 有“记忆”电流的性质，是一种记忆元件 (memory element)。
u C uC uC (t0 ) U 0
uC
uC
uS UU00((tt0 )t0 )
1
(0.25s t 0.5s) (0.5s t 0.75s)
8t 8 (0.75s t 1s)
第10页/共160页
则电容电流为：
4
i
C
du dt
0 4
8
i(A) 4
(0 t 0.25s) (0.25s t 0.5s) (0.5s t 0.75s) (0.75s t 1s)
受控电压源表示去耦的等效电路模型：
i1
i2
L1 u1 M d i2
dt
L2
u M di1
2
dt
第28页/共160页
2. 线性耦合电感元件的串联和并联
（1）线性耦合电感元件的串联
i
u1
L1
u
M L2 u2
顺接
i
u1
u
L1 M
L2
u2
反接
i
u
Leq
u
u1
u2
(L1
di dt
M
di ) (M dt
di dt
在时间间隔[t0，t]内，电容元件吸收的能量为
t
t
q(t )
wC (t0,t)
t0 pCdt
uidt
t0
f (q)dq
q(t0 )
u
若q(t0)=0,则
wC
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

动态电路的时域分析习题10-1 设图（a ）、（b ）电路达到稳态，在0=t 时开关S 动作，试求图中所标电压、电流的初值。

C u L i L(a) (b)题10-1图S 开，等效图如图所示： S 闭：解：对(a)图当0t -=时，求(0)C u -10(0)(0)1510510C C u u V +-==⋅=+0t +=时，求123(0),(0),(0)i i i +++1+2+15-5(0)=(0)==0.5A 5+5i i 3(0)0i A +=（b ）S 开S 闭_(0)u (0)L u (0)L对(b)图当0t -=时，求(0)L i -(0)(0)2L L i i A +-==当0t +=时，求(0),(0)L L u u -+42(0)4L u +⨯+=(0)4L u +=-(0)2240u +=⨯-=10-2 电路如图所示，已知Ω==421R R ，Ω=23R ，H L 1=，V U S 121=，V U S 62=。

电路原来处于稳定状态，0=t 时，开关S 闭合，试求)0(+L i 和)0(+L u 。

题10-2 图 题10-2 图解：S 开S 闭当0t -=时，求(0)L i -223(0)(0)1S L L U i i A R R +-===+当0t +=时，求(0)L u +111813421253246(0)10(0)3L L i i i i i i i u u ++⎧⎫=⎪⎪=+⎧⎫⎪⎪⎨⎬⎨⎬+=⎩⎭⎪⎪=⎪⎪⎩⎭+=+=10-3 设图示电路达到稳态，在0t =时开关S 动作，试求(0)c u +、(0)L i +、(0)i +、dt du C /)0(+和(0)L di dt +。

(a)(b)解：当0t -=时，求(0),(0)c L u i --，等效电路如图（a ）R S U -+2S L15(0)(0).(60//20)530(60//20)C C u u V +-===+_1560(0)(0).0.2530(60//20)6020L L i i A +===++当0t +=时，求(0),(0)L c u i ++,等效电路如图（b ）(0)5200.250L u V +=-⨯=15101(0)0.253010c i A +-=-=(0)(0)1/6C C du i V s dt C ++== (0)(0)0A/s L L di u dt L++==10-4 设图示电路达到稳态，在0t =时开关S 动作，试求(0)c u +、(0)L i +、(0)R u +、(0)c du dt +和(0)L di dt +。

Ω20LL1H2H题10-3图 题10-4图解：S 开 S 闭：当0t -=时，求(0),(0)c L u i --(0)(0)0L L i i A +-==(0)(0)1c c u u V +-==当0t +=时，求 (0),(0)L c u i ++(0)0,(0)0,(0)0R L C u V u V i V +++===(0)(0)0/C C du i V s dt C ++== (0)(0)0A/s L L di u dt L++==10-5 图示电路，开关S 在t =0换路前电路已达稳态，试求(0)L i +、(0)c u +、++0 0dtdu dtdi C L和。

题 10-5 图解：S 开V 4)0()0(V 4)0( ;0)0(=⇒===++-+L C C L u u u i; s A 4000)0(; s V 102)0( ;A 2.0)0(0 0 5//==⇒⨯-==-=⇒+++++Lu dtdi Ci dtdu i L L C C C10-6 试画出V )]4()([)(--=t t t u εε的波形解：10-7 求图示电路的阶跃响应L i 和u ，并画出它们的波形。

解：电路戴维宁等效电路如图所示： 52()5()2oc u t t =⨯=δδ 59222o R =+=Ω 19L s R τ==()191010()(1)()1()99tt l i t e t e t τ--=-=-δδ()9910855[2()]5[]()810()999t t L u i t e t e t --=--=---=+δδδ10-8电路如图所示，求冲激响应c u 。

解：电路戴维宁等效电路如图所示()26()93oc t u t =⋅=δδ36236eq R ⨯==+Ω利用阶跃响应求冲击响应2()3oc u t =δ20.43eq R C s ==其阶跃响应为()()52221()1()33tR C eq tuc S e t e t V --=-=-δδ则冲击响应为()5522()552()()()()323t t uc c dS t u t e t e t V d t --==-⨯-=δδ10-9电路如图所示，求冲激响应L i 。

Ω5Li st /题10-7图CuL题10-8图 题10-9图解：利用阶跃响应求冲激相应()5,15OC eq U t R =ε=Ω 215eq L S R τ==,所以阶跃响应为: ()()113L t i S t e t A -τ⎛⎫=-ε ⎪⎝⎭,则冲激响应为：()()()15211532tLL di t i t e t A dt --⎛⎫==-ε ⎪⎝⎭10-10图示电路0=t 时开关打开，已知打开后，试求。

题10-10图解：利用阶跃响应求冲激相应， 画出戴维宁等效电路图，如图所示,10,100OC S eq eq U U R k R C ==Ωτ== 所以阶跃响应为：()()1001tS u C S U e t -⎛⎫=-ε ⎪⎝⎭，所以()()1001100t C S U t U e t --⎛⎫=-ε ⎪⎝⎭又()0.50.3U =，所以30.15S U V =-10-11图示电路时开关断开。

已知，求电容。

C题10-11图解：此电路为零状态响应，开关断开可知1tRCC S U U e -⎛⎫=- ⎪⎝⎭,所以10,10k S eq U V R Ω==所以()410101t C t U t e -⎛⎫=- ⎪ ⎪⎝⎭,,又因为(2)8V C u =所以，当2t S =时，124F C =μ10-12电路如图所示，已知V U S 24=，Ω=31R ，Ω=62R ，Ω=43R ，Ω=24R ，F C 61=。

0=t 时，开关S 断开，求)(t u C ，)(t i C 。

题10-12图解：Ω=⨯=+++⨯=31266)(432432R R R R R R RV R R R U u S C 1233324)0(1=+⨯=+⨯=-由换路定理，V u u C C 12)0()0(==-+。

再由终值电路可知，0)(=∞C u ； … 时间常数S RC 5.0613=⨯==τ。

… 利用三要素法：0 12)]()0([)()(2≥=∞-+∞=--+t V e e u u u t u t tC C C C ，τ…由电容的VAR 知：0412261)(22≥-=⨯⨯-==--t A e e dt du Ct i t t C C ， 10-13图示电路原处于稳态。

若t =0时将开关S 由位置“1”打向位置“2” ，且在t =5秒时再将开关S 由位置“2”打向位置“1”。

试用三要素法求t ＞0的u C (t )，并绘出其波形。

题10-13图解：V ;100)0()0(-==-+C C u u.s 5 V,e 200100)( s;2 V;100)(V;100)5()5(; s 50 V,e 200100)(s;1 V;100)()5(5.02211≥+-==-=∞==≤≤-===∞---+-t t u u u u t t u u t C C C C t C C ττ其波形图如下图所示。

10-14图示电路原处于稳态。

若t =0时将开关S 由位置“a ”打向位置“b ” ，试用三要素法求t ＞0的u (t )，并绘出其波形。

题10-14图：V ;122224)( V ;8)0()0(=⨯+⨯=∞-==-+u u u. 0 V,e 2012)(; s 1 ,10≥-==Ω=-t t u R tτ 其波形图如下图所示。

10-15含受控源电路如图所示。

当0=t 时开关S 闭合。

求)(t u C ，0≥t 。

题10-15图u Vu 1224122)0(1243)0(++⨯==⨯=-t , s10-16电路如图所示，当t =1s 时开关闭合，闭合前电路已达稳态。

试求)(t i ，s 1≥t 。

题10-16图Vu u C C 60)0()0(==-+V u C 24)(=∞Ω=6o R 03624 )2460(24)(12261212≥+=-+==⨯==--t V e e t u s C R t t C o τ24V)(∞C＋'U －←R o10-17图示电路在换路前已达稳态。

当时开关接通，求的。

题10-17图24 6 8得10-18图10-18所示含受控源电路无初始储能。

求)(t u C 、)(1t u ，0 t 。

题10-18图变换电路Ω==4.052110u u R， ，10-19试分别就以下情形判断图示二阶电路在电压源电压值突然变化后所发生过渡过程的阻尼状态。

(1) L =1.5H ；(2) L =2H 。

题10-19解：换路且除源后为GCL 并联，且：.2125.0 )2(;3125.0 )1(临界阻尼状态欠阻尼状态⇒===⇒=<=L C G L C G10-20 RLC 串联电路的Ω=K R 4，H L 4=，F C μ1=。

该二阶电路的暂态响应属于什么情况（欠阻尼、过阻尼、临界阻尼），为什么？解：因为：6621014441016-⨯⨯==⨯=C L R ∴ 属于临界阻尼情况10-21 电路如图所示，以u 为变量列出电路的微分方程。

C uu题10-20图 题10-21图。