PQ变换与DQ变换的理解与推导

dq坐标系数学模型引言：dq坐标系是一种常用的坐标系，广泛应用于数学模型中。

本文将介绍dq坐标系的基本概念、转换公式以及在数学模型中的应用。

一、dq坐标系的基本概念dq坐标系是一种以dq轴为基础的坐标系，其中d轴表示直流分量，q轴表示交流分量。

在dq坐标系中，任意向量可以表示为d轴和q 轴的线性组合，即：Vd = V * cos(θ)Vq = V * sin(θ)其中V为向量的幅值，θ为向量的角度。

二、dq坐标系的转换公式在dq坐标系中，向量的转换可以通过dq坐标系的变换公式来实现。

dq坐标系的转换公式如下：Vα = Vd * cos(θ) - Vq * sin(θ)Vβ = Vd * sin(θ) + Vq * cos(θ)其中Vα和Vβ为向量在α轴和β轴上的分量，θ为dq坐标系与αβ坐标系之间的夹角。

三、dq坐标系在数学模型中的应用1. 电力系统中的dq坐标系dq坐标系在电力系统中广泛应用于电压和电流的分析和控制。

通过dq坐标系的转换，可以将电压和电流从三相坐标系转换到dq坐标系，简化了电力系统的分析和控制过程。

2. 电机控制中的dq坐标系dq坐标系也被广泛应用于电机控制领域。

通过dq坐标系的转换，可以将电机的电流从三相坐标系转换到dq坐标系，实现对电机的精确控制。

3. 电力电子领域中的dq坐标系dq坐标系在电力电子领域中也有重要的应用。

通过dq坐标系的转换，可以对电力电子器件的电流进行精确控制，提高电力电子系统的效率和稳定性。

4. 机器人控制中的dq坐标系dq坐标系在机器人控制中也有广泛的应用。

通过dq坐标系的转换，可以将机器人的位姿从笛卡尔坐标系转换到dq坐标系，实现对机器人的精确控制。

结论：dq坐标系是一种常用的坐标系，广泛应用于数学模型中。

本文介绍了dq坐标系的基本概念、转换公式以及在数学模型中的应用。

dq 坐标系的应用领域广泛，包括电力系统、电机控制、电力电子和机器人控制等。

通过dq坐标系的转换，可以简化数学模型的分析和控制过程，提高系统的效率和稳定性。

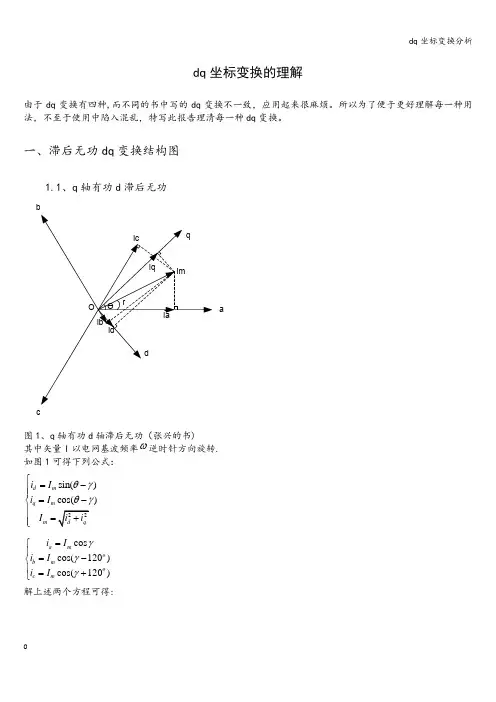
dq 坐标变换的理解由于dq 变换有四种,而不同的书中写的dq 变换不一致，应用起来很麻烦。

所以为了便于更好理解每一种用法，不至于使用中陷入混乱，特写此报告理清每一种dq 变换。

一、滞后无功dq 变换结构图1.1、q 轴有功d 滞后无功abc图1、q 轴有功d 轴滞后无功（张兴的书)其中矢量I 以电网基波频率ω逆时针方向旋转.如图1可得下列公式：sin()cos()d m q m m i I i I I θγθγ⎧=-⎪⎪=-⎨⎪=⎪⎩cos cos(120)cos(120)a m o b m o c m i I i I i I γγγ=⎧⎪=-⎨⎪=+⎩解上述两个方程可得:0cos cos(120)cos(120)2sin sin(120)sin(120)3111222o oq a o o d b c i i i i i i θθθθθθ⎡⎤⎢⎥-+⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦ 0sin cos 1sin(120)cos(120)1sin(120)cos(120)1a d o o b q o o c i i i i i i θθθθθθ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦⎣⎦1。

2、d 轴有功q 滞后无功相对应的d 轴有功、q 轴滞后无功的换算方法,只需将以上公式的d 、q 对换即可。

二、超前无功dq 变换结构图2.1、d 轴有功q 超前无功abc图2、d 轴有功q 轴超前无功如图1可得下列公式：cos()sin()d m q m m i I i I I θγθγ⎧=-+⎪⎪=-+⎨⎪=⎪⎩cos cos(120)cos(120)a m o b m o c m i I i I i I γγγ=⎧⎪=-⎨⎪=+⎩解上述两个方程可得：0sin()sin(120)sin(120)2cos()cos(120)cos(120)3111222sin sin(120)sin(120)2cos cos(120)cos(120)3111222o o q a o o d b c o o a o o b i i i i i i i i i θθθθθθθθθθθθ⎡⎤⎢⎥--+--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=--+--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦⎡⎤⎢⎥----+⎢⎥=-+⎢⎥⎢⎥⎢⎥⎣⎦c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦00cos()sin()1cos(120)sin(120)1cos(120)sin(120)1cos sin 1cos(120)sin(120)1cos(120)sin(120)1a d o o b q o o c d o o q o o i i i i i i i i i θθθθθθθθθθθθ--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-+-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦-⎡⎤⎡⎤⎢⎥⎢⎥=---⎢⎥⎢⎥⎢⎥⎢⎥+-+⎣⎦⎣⎦2。

单相谐波dq变换一、引言单相谐波dq变换是电力系统中常用的一种数学工具，它可以将三相交流电信号转换为直流信号，并且可以方便地进行控制和分析。

在本文中，我们将介绍单相谐波dq变换的基本原理、公式推导以及应用案例。

二、基本原理单相谐波dq变换是通过对三相交流电信号进行坐标变换来实现的。

具体来说，我们可以将三相交流电信号表示为：$V_{abc}=V_a+jV_b+j^2V_c$其中，$j$是虚数单位，$V_a$、$V_b$和$V_c$分别表示三个相位的电压。

通过dq坐标系变换，我们可以将这个三维向量表示为两个二维向量：$\begin{bmatrix}V_d \\V_q \\\end{bmatrix}=\begin{bmatrix}\cos\theta & -\sin\theta \\\sin\theta & \cos\theta \\\end{bmatrix}\begin{bmatrix}V_a \\V_b \\\end{bmatrix}$其中，$\theta=\omega t+\phi$是旋转角度，$\omega$是角速度，$\phi$是初始相位差。

这个矩阵就是dq坐标系变换矩阵，也称为Park变换矩阵。

通过dq坐标系变换，我们可以将三相交流电信号转换为直流信号。

具体来说，$V_d$表示直流分量，$V_q$表示交流分量。

如果我们只关注交流分量，那么可以将dq变换视为一种滤波器，它可以将不同频率的信号进行分离。

三、公式推导dq坐标系变换矩阵的推导比较复杂，需要用到一些高等数学知识。

这里简单介绍一下基本思路。

首先，我们需要将三相电压表示为复数形式：$V_a=|V_a|\cos(\omega t+\phi_a)$$V_b=|V_b|\cos(\omega t+\phi_b-2\pi/3)$$V_c=|V_c|\cos(\omega t+\phi_c+2\pi/3)$其中，$\phi_a$、$\phi_b$和$\phi_c$分别是三个相位的初始相位差。

dq坐标系功率
“dq坐标系”通常是电力系统中用于描述三相交流电系统中的矢量分析的坐标系。

这个坐标系在电力系统中有着重要的应用，特别是在控制、保护和分析交流电机以及变流器等方面。

dq坐标系（也称为帕克（Park）变换）：
- 描述：dq坐标系是从三相坐标系（abc坐标系）中变换得到的，通过旋转变换将三相系统转换为以直流或定子为参考的二维坐标系。

- 变换原理：dq坐标系通过dq变换将三相系统转换为两个轴：d轴（直流轴）和q轴（交流轴）。

d轴通常与系统的直流分量相关联，而q轴则与系统的交流分量相关。

- 功率分析：在dq坐标系下，电力系统的功率计算和分析更为方便。

在恒定转速的电机中，d轴代表有功功率，q轴代表无功功率。

功率在dq坐标系下的表示：
- 有功功率（P）和无功功率（Q）：在dq坐标系中，有功功率（P）位于d轴，无功功率（Q）位于q轴。

- 合成功率（S）：合成功率（S）为d轴和q轴上功率的矢量和，即\(S = P + jQ\)。

dq坐标系在控制和分析交流电机、变流器和电力系统中具有广泛的应用，它简化了三相电系统的分析和控制，使得在控制系统中对电压、电流和功率的处理更为方便和直观。

基于d—q变换的微电网PQ控制作者：侯海涛霍彦明焦立春来源：《山东工业技术》2017年第15期摘要：基于d-q变换的前馈解耦PQ控制，可使微电源发出的有功及无功功率恒定，是目前微电网的主流控制策略之一。

本文采用MATLAB中的SIMULINK模块搭建了系统仿真模型。

该模型中的并网逆变器在输出有功功率的同时补偿一定量的无功功率，并且使用了LCL 滤波器技术、锁相环技术。

为了使用参数时更加方便，本文对某些参数进行了标幺化。

最后通过运行仿真模型测得THD畸变略小，达到了控制要求。

关键词：变换；微电网；PQ控制DOI：10.16640/ki.37-1222/t.2017.15.1601 恒PQ控制策略PQ控制主要用于并网运行模式，是指对并网逆变器输出的有功功率和无功功率进行控制[2]。

由式1-1可知电网电压存在着耦合关系：（1-1）为了实现解耦控制需要从静止abc坐标系下转换为dq坐标系（称为Park变换，或dp变换）。

经过dp变换可得：（1-2）ud和uq均为常数实现了解耦控制。

PQ控制策略框图如图1所示。

三相交流电通过锁相环（PLL）得到电压和电流的相位，该角度用于Park变换中。

三相电压和电流经过Park变换，得到dq0分量。

通过式子（1-2）可以得到逆变器输入的参考无功功率和有功功率。

（1-3）再通过PQ计算器得到控制电流。

将控制电流与实际值比较，将结果输入到PI控制器中，最后转换到abc静止坐标系下得到并网逆变器输出的三相交流电。

2 PQ控制策略MATLAB/SIMULINK模型搭建2.1 LCL滤波器的设计微电网在并网时可看做受控电流源。

其中的逆变器发出的电流波形具有一定的谐波，为了抑制其产生的谐波，提高并网质量，通常需要接通低通滤波器。

在传统的微电网中采用L滤波器。

为了抑制高次谐波需要增大电感值，这样所使用的电感体积增大，会对整个系统带来一定的损耗。

为了解决以上问题，本文采用LCL滤波器。

dq变换的物理意义DQ变换是离散时间系统分析和控制中最基本的一种数学工具。

它最大的优点是能够在离散时间系统中直接地分析和控制交流电路等连续时间系统。

DQ变换主要是用来将三相交流电系统的三相电信号转换为两相静态坐标系下的直流（DC）和交流（AC）信号。

DQ变换在电力电子学、电力驱动系统和电力负载等领域里得到了广泛的应用。

DQ变换物理意义之一是将三相传感器输出的原始信号转换为直流和交流信号。

在交流电路中，电源产生的电流和电压通常是交流的，即其值随时间而变化。

然而，这些交流信号在控制系统中很难被处理，因为它们是在连续时间域中测量的。

通过DQ变换，交流信号可以被转换成在直流分量和交流分量上分别独立表示的信号，使得这些信号更容易被数学模型所处理。

因此，DQ变换为控制交流电路提供了更方便的数学工具。

DQ变换物理意义之二是将三相交流信号变换为定向坐标系下的信号。

在交流电力系统中，电源电压和电流是通过交流方式进行传输的，这意味着它们的值会随时间而变化。

DQ变换可以将三相信号转换成在定向坐标系下的幅值和相位，使得它们更容易被处理和控制。

通过在定向坐标系下进行运算，可以把三相交流系统的运算推广到定向坐标系下的系统，这为对三相电路的控制和运行提供了合理的数学模型和操作手段。

DQ变换物理意义之三是将转速不确定的交流平衡系统中的控制器输出变换到 DQ 轴上。

在电力电子学领域中，DQ变换被广泛应用于控制交流电机的速度。

在控制交流电机的速度时，控制器需要对转速进行测量，以便在电机达到理想的运行速度时进行控制。

然而，由于各种原因，控制器输出的速度信号可能会发生变化。

此时，DQ变换可以将非精确的控制器输出转换成在DQ轴上的精确的信号，使控制精度得到提高。

通过这种方法，DQ变换不仅可以提高交流电机的控制精度，而且也可以在各种实际应用中提高控制系统的可靠性和性能。

pq分解法与牛拉法的关系1.引言1.1 概述概述部分应该对PQ分解法和牛拉法的基本概念进行介绍，并说明它们之间的关系。

以下是可能的概述内容：引言PQ分解法和牛拉法是数学和计算机科学中两种重要的解决问题的方法。

它们在数学建模、优化问题求解以及科学和工程领域中具有广泛的应用。

尽管两种方法在原理和应用方面有所不同，但它们有一些相似之处，可以相互补充和结合使用。

PQ分解法是一种常用的线性代数方法，用于将复杂的矩阵运算简化为更易处理的形式。

它通过将矩阵分解为两个特殊形式的矩阵P和Q的乘积来实现。

其中，P矩阵是一个列正交矩阵，Q矩阵是一个行正交矩阵。

PQ分解法可以降低计算复杂性，减少矩阵运算的时间和空间复杂度，并提高计算效率。

另一方面，牛拉法是一种迭代算法，用于求解函数的极值。

它基于泰勒级数展开的思想，通过不断的迭代计算来逼近函数的最优解。

牛拉法在数学优化、信号处理、机器学习等领域被广泛应用，能够高效地找到函数的局部极值点。

尽管PQ分解法和牛拉法在目的和应用领域上存在一定的差异，但它们之间也有一些共同之处。

例如，牛拉法可以使用PQ分解法来简化矩阵运算，从而加快计算速度。

同时，PQ分解法可以辅助牛拉法进行高维函数的优化问题求解，增强算法的鲁棒性和可行性。

本文将对PQ分解法和牛拉法的基本原理、应用领域进行详细介绍，并探讨它们之间的关系。

同时，我们还将对两种方法的优缺点进行比较分析，展望它们在未来的应用前景。

通过对这两种方法的深入研究，我们可以更好地理解它们在解决实际问题中的作用，为相关领域的研究和应用提供指导和参考。

1.2文章结构文章结构部分的内容应包括对整篇文章的章节划分和各个章节的主要内容的介绍。

文章1.2 文章结构：本文主要分为引言、正文和结论三个部分。

引言部分包括概述、文章结构和目的三个小节。

概述部分简要介绍了PQ分解法和牛拉法，并提出了它们之间的关系的研究问题。

文章结构部分介绍了整篇文章的章节划分和各个章节的主要内容。

SVPWM、αβ变换、dq变换【转账】倪⼯⾸次发技术类的博⽂，开始在这⾥的记录了。

倪⼯想，尽量能发表些⾃⼰所思所想的东西为好。

如果有些觉得有必要转载的，倪⼯也会与⼤家分享。

今天学习了SVPWM、αβ变换、dq变换这些。

之前学过的都忘光了。

SVPWM主要是针对三相交流电机做转速控制时，为了在三相逆变桥的交流输出端输出期望的交流电压波形⽽采⽤的⼀种PWM调制技术。

针对三相全桥的六个开关管，共有6个有效状态以及2个零状态。

参考电压由两个相邻的空间⽮量合成（如果⼀个扇区时间内，这两个相邻⽮量的时间总和⼩于该扇区时间，那么就⽤零⽮量来填充）。

每个基本⽮量作⽤的⼤⼩，⽤其作⽤的时间长短来表⽰。

将这些基本⽮量按照⼀定的时间⽐例和实现顺序合成参考电压⽮量，从⽽得到需要的正弦电压波形。

选择不同的控制策略，影响输出电压的谐波含量和开关损耗。

SVPWM控制涉及到三相静⽌坐标系到两相静⽌坐标系的αβ变换，以及两相静⽌坐标系到两相旋转坐标系的dq变换，从⽽得到类似直流电机控制模型的两个正交参考向量，简化了对三相参考向量的控制。

这种思路来源于对三相异步电机的控制较为复杂这⼀事实。

通过三相异步电机的转矩公式可知，异步电动机的转速不仅与转⼦电流和⽓隙磁通有关，⽽且与转⼦回路的功率因数有关，⽽转⼦电流和⽓隙磁通两个变量既不正交，彼此也不相互独⽴。

转矩的这种复杂性，是异步电机难以控制的真正原因。

如果能将交流电机的物理模型等效地转换为类似直流电机的模型，分析和控制就可以⼤⼤简化。

αβ变换（⼜叫Clarke变换）是⼀种⽤来简化三相电路分析的数学变换。

它将向量信号投影到两相静⽌坐标系内。

它的⼀个很有⽤的应⽤是：为三相逆变器的SVPWM控制⽣成参考信号。

dq变换（⼜叫Park变换）与αβ变换有些类似，不同之处在于，它将向量信号投影到两相旋转的坐标系内。

常常⽤这种⽅法来简化对三相同步电机的分析，简化对三相逆变器控制的计算。

好了，今天的学习就点到这⾥了。

冲激采样变换对通常是指冲激信号（impulse train）与某个函数的采样变换之间的关系。

下面是一个简单的推导过程：
定义冲激信号：冲激信号是一个离散时间信号，其中在一个时间点上信号的值为1，在其他时间点上信号的值为0。

这个时间点称为冲激时刻。

定义采样变换：对于一个连续时间信号f(t)，其采样变换是在每个冲激时刻对f(t)进行采样，即将f(t)的值限制在每个冲激时刻的函数值。

推导冲激采样变换对：对于一个连续时间信号f(t)，其冲激采样变换可以表示为：
f_sampled(t) = f(t) * imp(t)
其中f_sampled(t)表示f(t)的冲激采样变换，imp(t)表示冲激信号。

这个公式表明，对于每个冲激时刻，f(t)在该时刻的值被采样，并且乘以冲激信号的值1。

解释冲激采样变换对的应用：冲激采样变换对在信号处理中有很多应用，例如在数字信号处理中，可以将连续时间信号转换为离散时间信号，以便在数字系统中进行处理和传输。

通过使用冲激采样变换对，可以在离散时间系统中准确地表示连续时间信号。

需要注意的是，以上推导是基于离散时间信号和连续时间信号的采样变换。

在实际应用中，还需要考虑采样率、量化误差等因素对信号处理结果的影响。

基于数学推导的方法进行Clark 变换和Park 变换网上很多关于Clark 变换和Park 变换都是基于磁链的，很多没有磁基础的同鞋，看了都很恍惚。

而且很多教科书上关于Clark 变换中的这个系数2/3，都是轻描淡写地一句话，根据能量守恒推导得到的！很多人看到这句之后一脸萌神！现在换个方式来进行Clark 和Park 变换的研究，用纯数学的方式来推导这个两个电力电子最唯美的变换！这两个变换是研究电力电子最基础的理论!在进行推导之前，帮助大家温习一下，三角函数的一些公式，估计很多人已经忘记了，没关系请继续往下看：三角函数积化和差公式：2β)cos(α-β)-cos(αsinβαsin2β)cos(αβ)-cos(αcosβαcos2β)(αs β)sin(αcosβinαin s 2β)(αs β)sin(αβs osαin in c 三角函数和差化积：2βαcos 2βαsin2sinβαsin 2βαsin2βαcos 2sinβαsin 2βαcos2βαcos 2βc osα os c 2βαsin2βαsin 2βc osα os c 其他一些三角函数：inβsinαβcos αcos β)os(αs c inβsinαβcos αcos β)os(αs cinβαc βcos αsin β)in(αs os s inβαc βcos αsin β)in(αs os s 将三相电用公式表示出来：3.........).........120t ωcos(2..........).........120-t ωcos(1..................).........t ωcos(mcm b m a UU U U U U 建立相对于电机定子的静止坐标系， U 为横轴， U 为纵轴，φ为旋转的磁场，α为旋转磁场和横轴的夹角。

如下图：UbUaUcaUαUβψ图1仔细观察三相电表达式和上图，似乎看出点规律来了！设：4.............................)t ωcos( U U U m a 将式（2）用三角函数的和差化积公式进行展开：)5..( (2)32123)t ωsin(21()t ωcos(23)t ωsin()21()t ω(cos()120sin()t ωsin()120cos()t ωcos()120-t ωcos( U U U U U U U U U U U U b m m b m b m b m b同理将式（3）进行展开：)6..( (2)32123)t ωsin()21()t ωcos()23)t ωsin()21()t ω(cos()120sin()t ωsin()120cos()t ωcos()120t ωcos( U U U U U U U U U U U U c m m c m c m c m c将电压表达式写成矩阵的形式：U U U U U cb a2323021211现在需要求出一个矩阵P 使得下式成立：cbaU U U P U U将式（4），式（5），式（6）联立方程组：)9..( (2)321)8..(....................2321)7.......(........................................U U U U U U U U c b a 用式（8）-式（9）得：U U U c b 3 U U U U c b a 30 (10)用式（8）+式（9）得：)11.(.................................................. U U U c b 将公式（7）两边同时乘以2得：)12.(..................................................22 U U a 这里为什么是乘以2而不乘以其他值，在数学领域是没有问题的，但是在工程应用中意义不大了，在后面的Park 变换中，大家就会明白为什么是乘以2，这里就不多说了，继续往下！将式（11）+式(12)得：)13..(........................................32 U U U U c b a 将式（10）和式（13）联立成方程组得：UU U U U U U U c b a c b a 31313233330 (14)好了到现在大家有没有发现，上面这个矩阵P 我们已经求出来了，也许看起来不是太明朗,下面做些变换：c b a c b a U U U U U U U U 33330313132 ................................(15)将式（15）写成矩阵的形式：cb a U U U U U3331333132 很多人又要问了为什么这个结果跟教科书上的不一样呢！好了下面做如下变换：)16....( (2)32123021132cb aU U U U U现在再看看这个结果是不是就和教科书上一样了，是不是感觉到数学工具很强大额，数学是个很好的工具，电子技术是将这些枯燥抽象的公式应用到具体的项目中，其实不管是什么技术都可以用数学的方式进行推导，计算机技术，电子技术，生物技术，仅仅是数学汪洋里的一艘小船！好了！上面即是美妙的Clark 变换,Clark 变换是基于电机定子建立的坐标系，还不能将电机等效成直流特性，下面我们还需要将电机的直流特性表征出来，怎么办呢！不用担心，下面接着进行Park 变换首先我们需要建立坐标系，选取磁场方向为d 轴方向，垂直于d 轴方向建立q 轴，然后将α、β轴投影到d 、q 轴上，θ为d 轴与α轴的夹角，因为q 轴代表无功，所以q 轴滞后d 轴90°，结果如下图：U bU aU caU αU βψU qU d图2有了上面这张图是不是就很简单了，让我们来看图说话吧，建立三角函数关系建立方程组：cos sin sin cos U U U U U U q d OK!将上式写成矩阵的形式：)17......(..............................cos sin sin cosU U U U qd 到现在已经出现点dq 变换的端倪了，离成功还差一步，继续努力！将式（16）带入到式（17）中：)18( (2)321230211sin sin cos 32cb aqd U U U con U U现在将矩阵进行展开：c b a qd U U U U Ucos 23sin 21cos 23sin 21sin sin 23cos 21sin 23cos 21cos 32好了将矩阵内部用函数的形式表示出来：cb a qd U U U U Ucos 120sin sin 120cos cos 120sin sin 120cos sin sin 120sin cos 120cos sin 120sin cos 120cos cos 32将上述三角函数的积化和差公式逆过来使用!cb a qd U U U U U)120sin()120sin(sin )120cos()120cos(cos 32O(∩_∩)O 哈哈！大功告成，dq 变换的神秘面纱已经被揭开了，现在再回过去看看前面的数学处理，是不是应该能明白为什么要那样处理了吧！很多人问磁场是怎样旋转起来的，下面我们几张图来研究下磁场旋转的机制！现在我们假想一下，有一台1对极对数的三相电机，我们从电机的侧面将其切开，三相绕组通上三相交流电，用法拉第右手定律绘制出绕组周围的磁场，结果如下图：上面的图为6个特殊位置下的磁场方向，实际中电流时连续变化的，所以磁场在电机内部也是连续变化的，连起来看上图时发现磁场在电机内部是旋转的！这篇主要是讲述了dq变换的原理及推导，后面一篇将推出dq变换在实际项目中的一些应用。