MATLAB中的abc-dq相坐标变换

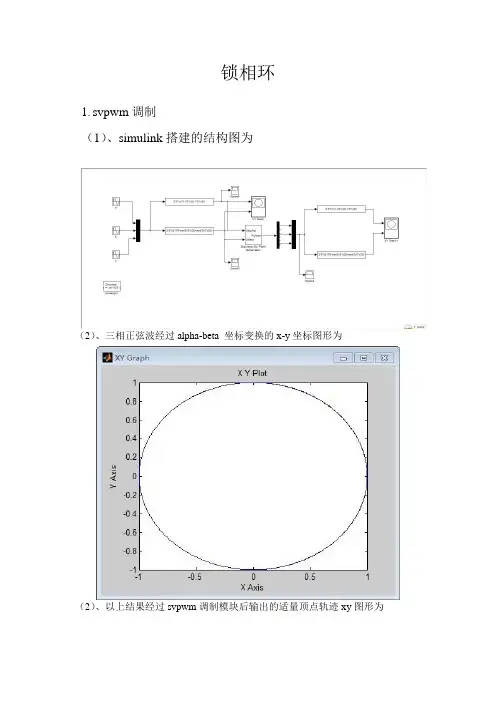
锁相环
1.svpwm调制
（1）、simulink搭建的结构图为
（2）、三相正弦波经过alpha-beta 坐标变换的x-y坐标图形为
（2）、以上结果经过svpwm调制模块后输出的适量顶点轨迹xy图形为
2
2、三相锁相环的设计
（1）、三相锁相环的原理为
三相锁相环的基本原理是基于坐标变换，采用静止坐标变换和同步坐标变换完成鉴相功能（将输入的三相电压经过坐标变换输出输入电压（相位给定）与输出信号的相位差），然后经过滤波器将高频信号过滤，经过pi调节器锁定到输入信号的频率，然后经过积分器对频率w进行积分得到电角度。

最后将输出反馈到输入端，构成闭环系统。

（2）、结构框图为
Pll局部结构图为
（3）、仿真结果与分析1 三相电源中含有谐波电源波形含有五次谐波
电源波形
仿真结果为
当三相电源不平衡时
仿真结果图为
电源波形为
仿真结果图为
对以上仿真结果的具体分析为
如果电源中含有直流分量，在进行abc到dq变换过程中直流分量会自动消失掉，故输出波形中不会含有直流分量
当电源中含有谐波时变换以后会是一个正弦量这个时候在系统
中添加一个滤波器将高频信号过滤掉即可。

其实锁相环最终的输出量为与输入量同相位的基波分量。

3 单相锁相环的设计
结构图为
pll具体结构图为
该仿真电源含有三相谐波。

一种电流源型三相逆变器模型申中鸿;杨林;蒋春旭【摘要】A 3-phase current-source inverter is mathematically modeled and analyzed in this paper.Firstly,the basic coordinate transformation is described;secondly,this paper derives a mathematical model of 3-phase current-source inverter in the d-q coordinate system and gives its block diagram;lastly,this paper analyzes the parameters related to the inverter,including power factor,harmonic state and output filter design.%对电流源型三相逆变器进行数学建模与分析。

首先介绍了基本的坐标变换；其次以电流源型三相逆变器的原理为基础，在d-q坐标系下，推导出其数学模型，并画出了结构框图；最后分析了逆变器的相关参数，包括功率因数、谐波状态和输出滤波器设计。

【期刊名称】《电气自动化》【年(卷),期】2014(000)005【总页数】4页(P12-14,50)【关键词】电流源型三相逆变器;坐标变换;建模;参数设计;滤波器【作者】申中鸿;杨林;蒋春旭【作者单位】工业和信息化部电子第五研究所，广东广州 510610;工业和信息化部电子第五研究所，广东广州 510610;工业和信息化部电子第五研究所，广东广州 510610【正文语种】中文【中图分类】TM460 引言近年来，随着微电子技术的快速发展，电力电子变换技术从中受益良多，获得了迅猛的发展，被世界各国学者视为人类社会的第二次腾飞。

摘要近年来，随着电力半导体器件及微电子器件特别是微型计算机及大规模集成电路的发展，再加上现代控制理论，特别是矢量控制技术向电气传动领域的渗透和应用，使得交流电机调速技术日臻成熟。

以矢量控制为代表的交流调速技术通过坐标变换重建电机模型，从而可以像直流电机那样对转矩和磁通进行控制，交流调速系统的调速性能已经可以和直流调速系统相媲美。

因此，研究由矢量控制构成的交流调速系统已成为当今交流变频调速系统中研究的主要发展方向。

最后，综合矩阵变换的控制策略及异步电动机转子磁场定向理论，采用计算机仿真方法分别建立了矩阵变换仿真模型以及基于矩阵变换的异步电动机矢量控制系统仿真模型，对矩阵变换的控制原理、输入、输出性能以及矢量控制系统的优质的抗扰能力及四象限运行特性进行分析验证，展现了该新型交流调速系统的广阔发展前景，并针对基于矩阵变换的异步电动机矢量控制系统的特点，着重对矢量控制单元进行了软件设计。

关键词：坐标变换矢量控制异步电动机仿真ABSTRACTIn recent years, with the development of the power semiconductor device，the microelectronics component, the microcomputer and large-scale integrated circuit and modern control theory, especially the penetration from vector control technology to electric drive field and application, the feasible AC motor speed regulation technology has become more mature day by day.Depend on the control principle of the MC and the rotor-flux orientation theory, and using the computer simulation technology, the simulation model of the MC and the matrix converter fed induction motor vector control drive system has been build. The input-output characteristic and the ability of four-quadrant operation have been testified, which has proved that the system has wide application field. The software of the vector control unit was designed at the end.Key words: matrix converter vector control induction motor simulation目录1.绪论 (1)1.1引言 (1)1.2 交流调速技术概况 (2)1.3 系统仿真技术概述 (3)1.4仿真软件的发展状况与应用 (4)1.5 MATLAB 概述 (4)1.6 Simulink 概述 (6)2.矢量控制理论 (7)2.1 异步电机的动态数学模型 (7)2.2 坐标变换 (10)2.2.1变换矩阵的确定原则 (10)2.2.2功率不变原则 (10)2.3矢量控制 (11)2.3.1 问题分析 (11)2.3.2直流电机的转矩控制 (12)2.3.3异步电机的转矩分析 (12)2.3.4 矢量控制原理 (12)3.总体模块设计 (15)3.1矢量控制结构框图 (15)3.2各子系统模块 (16)3.2.1求解磁链模块 (16)3.2.2 求解转子磁链角模块 (17)3.2.3 ids*求解模块 (17)3.2.4 iqs*求解模块 (17)3.2.5 ABC到DQ坐标变换模块 (18)3.2.6 DQ到ABC坐标变换模块 (18)3.3 电机参数设置 (19)3.4矢量控制环节模块 (21)3.5矢量控制的异步电动机调速系统模块 (21)4.Simulink 仿真 (23)5.结论 (28)致谢 (29)参考文献 (30)附录1 3s/2r坐标变换 (32)附录2 ω*=100和ω*=150时的比较 (34)1.绪论1.1引言工农业生产、交通运输、国防军事以及日常生活中广泛应用着电机传动，其中很多机械有调速要求，如车辆、电梯、机床及造纸机械等，而风机、水泵等为了减少损耗，节约电能也需要调速。

基于瞬时无功功率理论的瞬时电压dq 分解 为了提高电压凹陷检测算法的动态响应时间和检测精度，本文根据dq 变换后信号结构的特征，利用形态滤波原理，首次提出了形态学_dq 变换综合检测算法。

理论分析和实验研究表明该方法既保留了基于dq 变换电压凹陷检测方法原有的特点，同时也具有以下显著特征：具有更快的动态响应时问，通过选取合适的结构元素可以获取更高的检测精度。

[20]常见的三相电源系统是以ABC 坐标系统表示的，这种坐标在空间是静止不动的。

dq 坐标是由在空间以发电机同步旋转的两相坐标构成的。

从ABC 坐标系到dq 坐标系的变换称为派克变换。

将ABC 三相电压变换到dq 坐标的关系为：d q u u ⎡⎤⎢⎥⎣⎦=C a b c u u u ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦(3-1)式23()()()()00000022sin sin sin 3322cos cos cos 33w t w t w t w t w t w t ππππ⎡⎤-+⎢⎥⎢⎥----+⎢⎥⎣⎦变换阵C 中0sin w t 和0cos w t 是与扰动前a 相电压同相位的正负余弦信号。

将变换后dq 分量电压中的直流成分,d a U 和,q a U 提取出来，则可得,d a U 3cos sag U a （3-2）,q a U 3sin sag U a （3-3）式中sag U 为凹陷幅值，a 为相位跳跃角。

其中,d a U 和,q a U 经实测计算获得，则由式（2）（3）可求出凹陷电压的幅值和相位跳跃角。

22,,33sag d a q a U U U =+ (3-4) ,1122,,3sin sin 3q a sag d a q a U U a U U U --⎛⎫⎛⎫=-= ⎪ ⎪+⎝⎭ (3-5) 由此可见，低通滤波器的选择成了该算法的能否实用的关键，经过研究表明较为适合这个算法的滤波器是巴特沃斯2阶，截至频率c f =60Hz 的低通滤波器。

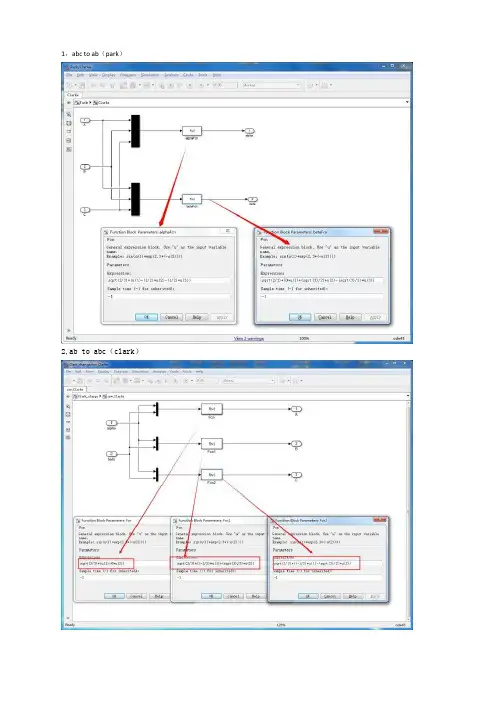
1，abc to ab（park）
2,ab to abc（clark）
4,dq to abc
6,dq to ab
注意，涉及到abc到dq的坐标变换时，要加时钟函数具体见前面。

参数如下
7，abc坐标系和αβγ坐标系之间的变换矩阵
考虑矩阵符号前面的因子后，以上变换矩阵的行向量分别是α、β、γ坐标轴上的单位向量在abc坐标系中的坐标。

变换矩阵的逆矩阵，实际上就是线性代数课程中所定义的由旧基（a、b、c轴的单位向量）向新基（α、β、γ轴的单位向量）的过渡矩阵。

此矩阵左乘某向量在abc坐标中的坐标向量，可得到该向量在αβγ坐标系中的坐标向量；此矩阵的逆矩阵左乘某向量在αβγ坐标中的坐标向量，可得到该向量在abc坐标系中的坐标向量。

若将abc坐标变换到αβγ坐标的同时还将所得αβγ坐标系中的向量旋转θ角度，这样的变换称为Park变换。

显然，abc坐标到αβγ坐标的变换矩阵是Park变换矩阵在θ=0时的特例
不同情况下公式的第三行不一样。

摘要采用电力电子变频装置实现电压频率协调控制，改变了同步电机历来的恒速运行不能调速的面貌，使它和异步电机一样成为调速电机大家庭的一员。

本文针对同步电机中具有代表性的凸极机，在忽略了一部分对误差影响较小而使算法复杂度大大增加的因素（如谐波磁势等），对其内部电流、电压、磁通、磁链及转矩的相互关系进行了一系列定量分析，建立了简化的基于abc三相变量上的数学模型，并将其进行派克变换，转换成易于计算机控制的d/q坐标下的模型。

再使用MATLAB中用于仿真模拟系统的SIMULINK对系统的各个部分进行封装及连接，系统总体分为电源、abc/dq转换器、电机内部模拟、控制反馈四个主要部分，并为其设计了专用的模块，同时对其中的一系列参数进行了配置。

系统启动仿真后，在经历了一开始的振荡后，各输出相对于输出时间的响应较稳定。

关键词：同步电机 d/q模型 MATLAB SIMULINK 仿真。

目录第1章引言 ........................................................................................................................................ - 1 - 1.1引言 (1)1.2同步电机概述 (1)1.3系统仿真技术概述 (2)1.4仿真软件的发展状况与应用 (2)1.5MATLAB概述 (2)1.6S IMULINK概述 (4)第2章同步电机基本原理 (5)2.1理想同步电机 (5)2.2 ABC/DQ模型的建立 (5)第3章仿真系统总体设计 (9)3.1系统对象 (9)3.2系统分块 (9)3.3控制反馈环节 (10)第4章仿真系统详细设计 (12)4.1总体设计 (12)4.2具体设计 (12)4.3控制反馈环节 (15)第5章系统仿真运行 (16)5.1输出结果稳定情况 (16)结论 (19)致谢 (20)参考文献 (21)第1章引言1.1引言世界工业进步的一个重要因素是过去几十年中工厂自动化的不断完善。

坐标变换总结姓名：日期：2011.11.4坐标变换的总结一．由三项坐标系变换到两相旋转坐标系1.三相到两相静止坐标系的变换首先，确定三相电压的相序：cos()2cos()34cos()3A m B m c m u U wt u U wt u U wt ππ==-=-在坐标图上表示三相到两相静止坐标系上的变换，如图所示：图13-2s 变换由上图，我们可以将A u 、B u 、c u转化到两相静止坐标系上，具体等式如下：211()3222()322A B C B C u u u u u αβ⎧=--⎪⎪⎨⎪=-⎪⎩插入系数2、3是为了保证两相坐标系中合成矢量的模与各相电压的模相同。

后面会推导为什么可以保证模不变。

整理成状态方程的形式，如下：1112223022A B C u u u u u αβ⎡⎤⎡⎤--⎢⎥⎡⎤⎢⎥⎢=⎢⎥⎢⎥⎢⎣⎦⎢⎥-⎣⎦⎢⎥⎣⎦2.两相静止坐标系到两相旋转坐标系的变换我们知道，在两相静止坐标系中，合成矢量是旋转的，我们令旋转坐标系的d 轴与旋转矢量重合，则可将其转换到旋转坐标系中。

坐标变换如图所示：图22s-2r 变换此时，我们可以得到，两相静止坐标系到两相旋转坐标系的公式，其中θ一般取为A 相的相角。

cos sin sin cos d q u u u u αβθθθθ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦二．反向变换1.若需要将旋转坐标系转化到静止坐标系上，只需相应的将d-q 向αβ-投影即可，根据图二，我们可以得到：cos sin sin cos d q u u u u αβθθθθ⎡⎤⎡⎤-⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦2.同理，根据图1，我们可以将αβ-分别投影到A 、B 、C 上，获得其逆变换：102133221322A B C u u u u u αβ⎡⎤⎢⎥⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎣⎦⎢⎥--⎢⎥⎣⎦三．关于乘以2/3保持模不变的问题首先，我们已经能够确定了电压相序cos()2cos()34cos()3A m B m c m u U wt u U wt u U wt ππ==-=-经过变换后：211()322A B c u u u u α=--进而，我们可以推知：211()322B AC U U U U α∙∙∙∙=--22211()211(1)32223()32A A A A A A U a U aU U a a U U ∙∙∙∙∙∙=--=--==其中，a=23j e π。

基于d—q变换的微电网PQ控制作者：侯海涛霍彦明焦立春来源：《山东工业技术》2017年第15期摘要：基于d-q变换的前馈解耦PQ控制，可使微电源发出的有功及无功功率恒定，是目前微电网的主流控制策略之一。

本文采用MATLAB中的SIMULINK模块搭建了系统仿真模型。

该模型中的并网逆变器在输出有功功率的同时补偿一定量的无功功率，并且使用了LCL 滤波器技术、锁相环技术。

为了使用参数时更加方便，本文对某些参数进行了标幺化。

最后通过运行仿真模型测得THD畸变略小，达到了控制要求。

关键词：变换；微电网；PQ控制DOI：10.16640/ki.37-1222/t.2017.15.1601 恒PQ控制策略PQ控制主要用于并网运行模式，是指对并网逆变器输出的有功功率和无功功率进行控制[2]。

由式1-1可知电网电压存在着耦合关系：（1-1）为了实现解耦控制需要从静止abc坐标系下转换为dq坐标系（称为Park变换，或dp变换）。

经过dp变换可得：（1-2）ud和uq均为常数实现了解耦控制。

PQ控制策略框图如图1所示。

三相交流电通过锁相环（PLL）得到电压和电流的相位，该角度用于Park变换中。

三相电压和电流经过Park变换，得到dq0分量。

通过式子（1-2）可以得到逆变器输入的参考无功功率和有功功率。

（1-3）再通过PQ计算器得到控制电流。

将控制电流与实际值比较，将结果输入到PI控制器中，最后转换到abc静止坐标系下得到并网逆变器输出的三相交流电。

2 PQ控制策略MATLAB/SIMULINK模型搭建2.1 LCL滤波器的设计微电网在并网时可看做受控电流源。

其中的逆变器发出的电流波形具有一定的谐波，为了抑制其产生的谐波，提高并网质量，通常需要接通低通滤波器。

在传统的微电网中采用L滤波器。

为了抑制高次谐波需要增大电感值，这样所使用的电感体积增大，会对整个系统带来一定的损耗。

为了解决以上问题，本文采用LCL滤波器。

同步电机模型的MATLAB仿真摘要采用电力电子变频装置实现电压频率协调控制，改变了同步电机历来的恒速运行不能调速的面貌，使它和异步电机一样成为调速电机大家庭的一员。

本文针对同步电机中具有代表性的凸极机，在忽略了一部分对误差影响较小而使算法复杂度大大增加的因素（如谐波磁势等），对其内部电流、电压、磁通、磁链及转矩的相互关系进行了一系列定量分析，建立了简化的基于abc三相变量上的数学模型，并将其进行派克变换，转换成易于计算机控制的d/q坐标下的模型。

再使用MATLAB中用于仿真模拟系统的SIMULINK 对系统的各个部分进行封装及连接，系统总体分为电源、abc/dq转换器、电机内部模拟、控制反馈四个主要部分，并为其设计了专用的模块，同时对其中的一系列参数进行了配置。

系统启动仿真后，在经历了一开始的振荡后，各输出相对于输出时间的响应较稳定。

关键词：同步电机 d/q模型 MATLAB SIMULINK 仿真。

The Simulation Platform of Synchronous Machine by MATLABAbstract:The utilization of transducer realizes the control of voltage’s frequency. It changes the situation that Synchronous Machine is always running with constant speed. Just like Asynchronous Machine, Synchronous machine can also be viewed as a member of the timing machine. This thesis intends to aim at the typical salient pole machine in Synchronous Machine. Some quantitative analysis are made on relations of salient pole machine among current, voltage, flux, flux linkage and torque, under the condition that some factors such as harmonic electric potential are ignored. These factors have less influence on error but greatly increase complexity of arithmetic. Thus, simplified mathematic model is established on the basis of a, b, c three phase variables. By the Park transformation, this model is transformed to d, q model which, is easy to be controlled by computer. Simulink is used to masking and linking all the parts of the system. The system can be divided into four main parts, namely power system, abc/dq transformation, simulation model of the machine and feedback control. Special blocks are designed for the four parts and a series of parameters in these parts are configured. The results of simulation show that each output has a satisfactory response when there is disturbance.Key Words: Synchronous Machine Simulation d/q Model MATLAB SIMULINK目录第1章引言 (1)1.1引言 (1)1.2同步电机概述 (1)1.3系统仿真技术概述 (2)1.4仿真软件的发展状况与应用 (2)1.5MATLAB概述 (2)1.6S IMULINK概述 (4)1.7小结 (5)第2章同步电机基本原理 (6)2.1理想同步电机 (6)2.2ABC/DQ模型的建立 (6)第3章仿真系统总体设计 (10)3.1系统对象 (10)3.2系统分块 (10)3.3控制反馈环节 (11)第4章仿真系统详细设计 (13)4.1总体设计 (13)4.2具体设计 (13)4.3控制反馈环节 (16)第5章系统仿真运行 (17)5.1输出结果稳定情况 (17)5.2小结 (20)第6章结论 (21)第7章致谢 (22)参考文献 (23)第1章引言1.1引言世界工业进步的一个重要因素是过去几十年中工厂自动化的不断完善。