2015届高考数学一轮复习 三角函数模型的简单应用练习 新人教A版必修4

高中数学学习材料鼎尚图文*整理制作§1.6三角函数模型的简单应用习题一、选择题：1、函数)421sin(2π+=x y 的周期，振幅，初相分别是（ ） A.4,2,4ππ B.4,2,4ππ-- C.4,2,4ππ D.4,2,2ππ 2、要得到函数cos(21)y x =+的图象,只要将函数cos 2y x =的图象（ ） A ．向左平移1个单位B ．向右平移1个单位C ．向左平移12个单位D ．向右平移12个单位 3、为了得到函数R x x y ∈+=),63sin(2π的图像，只需把函数R x x y ∈=,sin 2的图像上所有的点（ ） A ．向左平移6π个单位长度，再把所得各点的横坐标缩短到原来的31倍（纵坐标不变） B ．向右平移6π个单位长度，再把所得各点的横坐标缩短到原来的31倍（纵坐标不变） C ．向左平移6π个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变） D ．向右平移6π个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变） 4、把函数sin ()y x x =∈R 的图象上所有的点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数是（ ） A ．sin 23y x x π⎛⎫=-∈ ⎪⎝⎭R ， B ．sin 26x y x π⎛⎫=+∈ ⎪⎝⎭R ， C ．sin 23y x x π⎛⎫=+∈ ⎪⎝⎭R ， D ．sin 23y x x 2π⎛⎫=+∈ ⎪⎝⎭R ，5、如图，函数)0,0)(sin(πϕϕω<<>+=A x A y 的图象经过点)0,6(π-、)0,67(π，且该函数的最大值为2，最小值为－2，则该函数的解析式（ ）A.)423sin(2π+=x yB.)42sin(2π+=x yC.)623sin(2π+=x yD.)62sin(2π+=x y二、填空题7、函数sin()(0,0,0)y A x A ωϕπωϕ=+>-<<>在一个周期的区间上的图象如图，则A ＝ ，ω＝ ，ϕ＝ ．8、已知ω>0,0ϕπ<<,直线x =4π和x =54π是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,则w = ．三、解答题9、如图，某地一天从6时到14时的温度变化曲线近似满足函数b x A y ++=)sin(ϕω(1) 求这段时间最大温差；(2) 写出这段曲线的函数解析式．。

高一三角函数复习资料一、范例分析例1、 已知函数y=21cos 2x+23sinx·cosx+1 （x ∈R ）,（1）当函数y 取得最大值时，求自变量x 的集合；（2）该函数的图像可由y=sinx(x ∈R)的图像经过怎样的平移和伸缩变换得到？说明：这类题一般的解法是：先化成关于sinωx,cosωx 的齐次式，降幂后最终化成y=22b a +sin (ωx+ϕ)+k 的形式。

解：（1）y=21cos 2x+23sinx·cosx+1=41 (2cos 2x －1)+ 41+43（2sinx·cosx ）+1=41cos2x+43sin2x+45=21(cos2x·sin 6π+sin2x·cos 6π)+45=21sin(2x+6π)+45所以y 取最大值时，只需2x+6π=2π+2kπ,（k ∈Z ），即 x=6π+kπ,（k ∈Z ）。

所以当函数y 取最大值时，自变量x 的集合为{x|x=6π+kπ,k ∈Z}（2）将函数y=sinx 依次进行如下变换：（i ）把函数y=sinx 的图像向左平移6π，得到函数y=sin(x+6π)的图像； （ii ）把得到的图像上各点横坐标缩短到原来的21倍（纵坐标不变），得到函数y=sin(2x+6π)的图像；（iii ）把得到的图像上各点纵坐标缩短到原来的21倍（横坐标不变），得到函数y=21sin(2x+6π)的图像；（iv ）把得到的图像向上平移45个单位长度，得到函数y=21sin(2x+6π)+45的图像。

综上得到y=21cos 2x+23sinxcosx+1的图像。

例2()已知向量，，，，，，其中a x xb x xc =⎛⎝ ⎫⎭⎪=-⎛⎝ ⎫⎭⎪=-cos sin cos sin 32322231x R ∈.（I ）当a ⊥b 时，求x 值的集合；（）求的最大值。

II a c -解：（）由⊥·I a b a b →→→→⇔=0即··coscos sin sin 3223220x x x x -=则cos20x =()得22x k k Z =+∈ππ()∴x k k Z =+∈ππ24∴当⊥时值的集合为，a b x x x k k Z →→=+∈⎧⎨⎩⎫⎬⎭|ππ24解法一：（）II a c a c a a c c a a c c ||()||||→→→→→→→→→→→→-=-=-+=-+22222222又||c o s s i n a x x →=⎛⎝ ⎫⎭⎪+⎛⎝ ⎫⎭⎪=22232321()||c →=+-=222314a b x x x x x →→=-=-⎛⎝ ⎫⎭⎪=+⎛⎝ ⎫⎭⎪·332322323212322326cos sin cos sin cos π∴||c o s c o s a c xx→→-=-+⎛⎝ ⎫⎭⎪+=-+⎛⎝ ⎫⎭⎪214326454326ππ∴||m a xa c →→-=29∴||m i n a c →→-=3即的最大值为||a c →→-3解法二：||cos sin a c x x →→-=-+⎛⎝ ⎫⎭⎪22323321， =-⎛⎝ ⎫⎭⎪++⎛⎝ ⎫⎭⎪cos sin 32332122x x =-++++cos cos sin sin 223223323322321x x x x=-⎛⎝ ⎫⎭⎪+2323325sin cos x x =-⎛⎝ ⎫⎭⎪+43235sin x π∴||maxa c →→-=29∴||max a c →→-=3说明：三角函数与向量之间的联系很紧密，所以此类题目往往是命题人所青睐。

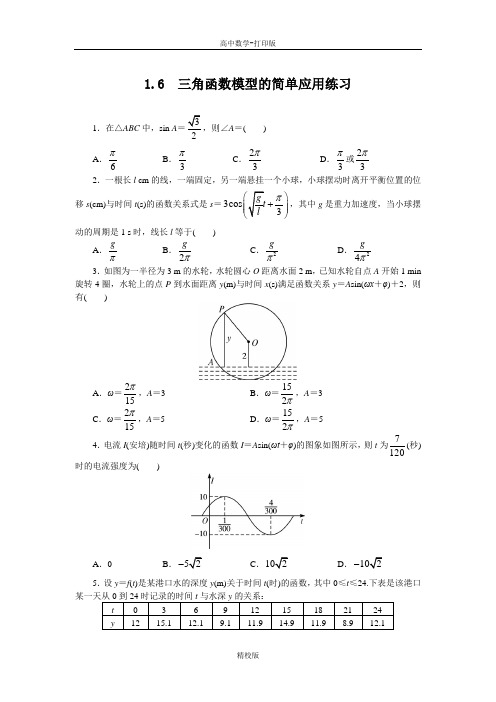
1.6 三角函数模型的简单应用练习1．在△ABC 中，sin A A ＝( ) A ．6π B ．3πC ．23π D ．3π或23π2．一根长l cm 的线，一端固定，另一端悬挂一个小球，小球摆动时离开平衡位置的位移s (cm)与时间t (s)的函数关系式是s ＝3cos 3π⎫+⎪⎪⎭，其中g 是重力加速度，当小球摆动的周期是1 s 时，线长l 等于( )A ．gπB ．2g πC ．2gπ D ．24g π3．如图为一半径为3 m 的水轮，水轮圆心O 距离水面2 m ，已知水轮自点A 开始1 min 旋转4圈，水轮上的点P 到水面距离y (m)与时间x (s)满足函数关系y ＝A sin(ωx ＋φ)＋2，则有( )A ．ω＝215π，A ＝3 B ．ω＝152π，A ＝3 C ．ω＝215π，A ＝5D ．ω＝152π，A ＝54．电流I (安培)随时间t (秒)变化的函数I ＝A sin(ωt ＋φ)的图象如图所示，则t 为7120(秒)时的电流强度为( )A ．0B ．-C ．D ．-5．设y ＝f (t )是某港口水的深度y (m)关于时间t (时)的函数，其中0≤t ≤24.下表是该港口经长期观测，函数y ＝f (x )的图象可以近似地看成函数y ＝A sin(ωt ＋φ)＋k 的图象．下面的函数中，最能近似地表示表中数据间对应关系的函数是( )A ．y ＝12＋3sin6t π，t ∈[0,24]B ．y ＝12＋3sin 6t ππ⎛⎫+ ⎪⎝⎭，t ∈[0,24] C ．y ＝12＋3sin12t π，t ∈[0,24]D ．y ＝12＋3sin 122t ππ⎛⎫+⎪⎝⎭，t ∈[0,24]6．已知x ∈(0,2π)，cos x ＝x ＝__________. 7．如图，是一向右传播的绳波在某一时刻绳子各点的位置图，经过半个周期后，乙点的位置将移至__________．8．如图某地夏天从8～14时用电量变化曲线近似满足函数y ＝A sin(ωx ＋φ)＋b .(1)这一天的最大用电量为__________万度，最小用电量为__________万度； (2)这段曲线的函数解析式为__________．9．如图，牡丹江市某天从6时到14时的温度变化曲线近似满足函数y ＝A sin(ωx ＋φ)＋0,0,.2b A πωϕ⎛⎫>><⎪⎝⎭(1)求这一天最大的温差； (2)求这段曲线的函数解析式．10．(能力拔高题)如图，某市拟在长为8 km的道路OP的一侧，修建一条运动赛道，赛道的前一部分为曲线段OSM，该曲线段为函数y＝A sin ωx(A＞0，ω＞0)，x∈[0,4]的图象，且图象的最高点为S(3,，赛道的后一部分为折线段MNP，为保证参赛运动员的安全，限定∠MNP＝120°.求A，ω的值和M，P两点间的距离．参考答案1. 答案：D2. 答案：D 3．答案：A 4. 答案：A 5. 答案：A 6. 答案：34π或54π 7. 答案：丁点8. 答案：(1)50 30 (2)y ＝10sin 66x ππ⎛⎫+⎪⎝⎭＋40，x ∈[8,14]9. 解：(1)由图象得这一天的最高温度是－2 ℃，最低温度是－12 ℃， 则这一天最大的温差是－2－(－12)＝10(℃)． (2)由(1)得2,12,A b A b +=-⎧⎨-+=-⎩解得A ＝5，b ＝－7.由图象得函数的周期T ＝2(14－6)＝16， 则216πω=，解得ω＝8π. 所以y ＝55sin 4πϕ⎛⎫+⎪⎝⎭－7. 由图象知点(10，－7)在函数的图象上， 则－7＝5sin 1078πϕ⎛⎫⨯+-⎪⎝⎭， 整理得5sin 4πϕ⎛⎫+ ⎪⎝⎭＝0， 又|φ|＜2π，则φ＝4π-.则这段曲线的函数解析式是y ＝5sin 784x ππ⎛⎫--⎪⎝⎭(6≤x ≤14)．10. 解：依题意，有A ＝4T ＝3，又T ＝2πω，∴ω＝6π.∴y ＝6x π.当x ＝4时，y ＝23π＝3，∴M (4,3)．又P (8,0)，∴|MP |5(km)=．。

1.6三角函数模型的简单应用（检测教师版）答案：C为80.故选C.2. 单摆从某点开始来冋摆动，离开平衡位置的距离S cm 和时间十s 的函数关系为S= 8sin （2n t+yj,那么单摆来回摆动一次所需的时|'可为（答案：D 解析：因为G =2 Ji,所以7=—= 1.（I.）时间：40分钟总分：60分班级:姓名:-、选择题（共6小题，每题5分，共30分）1. 某人血压满足函数式Az ）=24sin （160 Ji Z ）+110,其中为血压,（为时间，则此人每分钟心跳的次数为（A. 60B. 70C. 80D. 90解析：由于。

=160开，故函数的周期/=了,=80, 即每分钟心跳的次数B. nsC. 0.5 sD. 1 s3. 水平地面上发射的炮弹，初速度大小为ro,发射角为纥重力加速度为刃则炮弹上升的高度y 与飞行时间tZ 间的关系式为（）A. y= vol 1B. y= n )sin 0 t —~gtC. y= %sin 0 tD. y=旳cos 0 t答案:B解析：竖直方向的分速度K ）sin ",由竖直上抛运动的位移公式y= r o sin 0 t —^gt\故选B.4.单位圆上有两个动点从A ；同时从户（1,0）点出发, 沿圆周转动，弭点按逆时针方向转，速度 ^j-^-rad/s, N 点按顺时针方向转，速度为寸~rad/s,则它们出发后第三次相遇时各口走过的弧度数分别为（）B. D.答案：C解析：设IV 两点走过的弧长分别为Z 和厶，自出发至第三次相遇，经过七秒，则JI，2=亍・JI JI・・・百汁亍=6”，・・・Q12, ・・・22n,厶=4「5. 如图为2017年某市某天中6 h 至14 h 的温度变化曲线,其近似满足函数y=«inS+O ）+胡>0, 3>0, y<0<n 的半个周期的图彖，则该天8 h 的温度大约为（答案:D解析：由题意得 J=|x (30-10)=10,方=£x (30+10)=20. 72X(14-6)=16, A —=16,+20,将 x=6,尸 10 代入得 10sinlyX6+ 0 1+20、 JT “ 3 兀 An 3 nA 卜 0丿=一1,由于勺-〈0<兀，可得 ^=—, .•.y=10sin^—jr+—I的温度大约为13 °C,故选D ・6. 一根长/厘米的线，一端固定，另一端悬挂一个小球，小球摆动时，离开平衡位置的位移s （厘兀7. 电流/（mA ）随时间t （s ）变化的函数关系是/=3sinlOO7T f+y,则电流/变化的最小正周期、B. 15 °CC. 14 °CD. 13 °CJT(\・••尸 10sin (瓦卄 4>\= 10,即 sin]*20,[6, 14].当 ^=8 时，y=10sin|仔 X8+扌 n) + 20 = 20 —5电~13,即该天8 h米）和时间方（秒）的函数关系是：s=3cos jr+yj.已知尸980厘米/秒，耍使小球摆动的周期是1秒, 980 A. ------- c答案：C 245 C. _cm兀D.980 —cm 兀乡=980, 7=b 得 7=9801 — 245 "cm.二.填空题（共2小题，每题5分,共10分）A. 16 °C245解析：由周期线的长度应当是（），所以小球的摆动周期T=2 乂由1=\代入兀=3. 14, 2兀频率和振幅分别为 _____ , _______ , ______ . 答案:寺50 3解析：最小正周期7'=佥〜击；频率f#=50；振幅 43.8. 如图为一个缆车示意图，该缆车半径为4. 8 m,圆上最低点与地而距离为0. 8 m, 60秒转动一 圈，图中滋与地而垂直，以滋为始边，逆时针转动0角到处，设〃点与地面距离是力，则力 与（）间的函数关系式为 _____________________________ .解析:以0为原点建立坐标系，如右图，则以&为始边，处为终边的角为0 故点〃的坐标为（4.8cos （ “一*）, 4.8sin （ 0 三、解答题（共2小题，每题10分，共20分）9. 交流电的电压/单位：V ）随时间H 单位：s ）变化的关系式是上-220^sin （100 兀 H ■制，［0, +<^）.⑴求开始时（1=0）的电压；⑵求电压的最大值和首次达到最大值的时间:（3）求电压的最大值重复出现一次的时间间隔.解:（1）当十=0时，F=22甘Xsirr 才=11曾，即开始时的电压为11甘 V.（2）电压的最大值为220羽V.答案:：.h =5.6+4. 8sin 0当100Z+时，片血，即电压首次达到最大值的时间为肖S.（3）C 金'=帶，即电压的最大值重复出现一次的时间间隔为帶s.10. 电流强度/（A ）随时间Ms ）变化的关系式是/=〃sin （讥+ 0）/>0, 6>>0, Rl<y.⑴若/=〃sin （讥+ 0）在一个周期内的图彖如图所示，试根据图彖写出/=Ssin （少汁0） 的解析式；JI JI (IT A2 ,・•・ ^―, /= 300sini IOO TI t+—\（2）由题意，知幻岛，・・・G 2200H ,・•・正整数Q 的最小值为629.G 1UU⑵为了使I=Asin^t+ 0）中的£在任意一个血 的时间段内电流强度/能取得最大值与最小值，那么正整数G 的最小值是多少? 解：（1）由图，可知月=300.设心=一计了乙=吉，1 1 f2=60* - T=tl ~U=^300・•・4=耳=100兀，・・・7=300sin(100兀z+O).将為0）代入解析式,, JI得—e=Ji .. Ji A (/>=—+2kTi , kEZ V R | <—,。

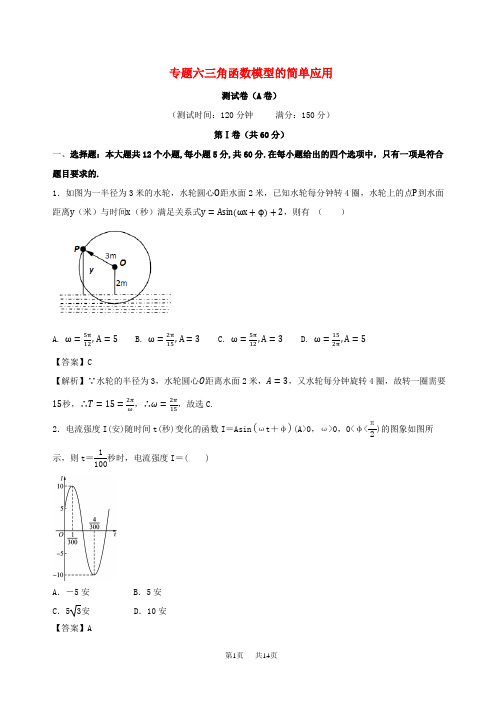
专题六三角函数模型的简单应用测试卷（A 卷）（测试时间：120分钟 满分：150分）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．如图为一半径为3米的水轮，水轮圆心O 距水面2米，已知水轮每分钟转4圈，水轮上的点P 到水面距离y （米）与时间x （秒）满足关系式y =Asin(ωx +ϕ)+2，则有 （ ）A. ω=5π12,A =5 B. ω=2π15,A =3 C. ω=5π12,A =3 D. ω=152π,A =5【答案】C【解析】∵水轮的半径为3，水轮圆心O 距离水面2米，A =3，又水轮每分钟旋转4圈，故转一圈需要15秒，∴T =15=2πω，∴ω=2π15，故选C.2．电流强度I(安)随时间t(秒)变化的函数I ＝Asin ()ωt ＋φ(A>0，ω>0，0<φ<π2)的图象如图所示，则t ＝1100秒时，电流强度I ＝( )A ．－5安B ．5安C ．53安D ．10安 【答案】A3．某商品一年内每件出厂价在5千元的基础上，按月呈f(x)＝Asin(ωx＋φ)＋B(A>0，ω>0，|φ|<π2) 的模型波动(x 为月份)，已知3月份达到最高价7千元，7月份达到最低价3千元，根据以上条件可以确定f(x)的解析式是( )A ．f(x)＝2sin ⎝ ⎛⎭⎪⎫π4x ＋π4＋5(1≤x≤12，x ∈N *)B ．f(x)＝7sin ⎝ ⎛⎭⎪⎫π4x －π4＋5(1≤x≤12，x ∈N *)C ．f(x)＝7sin ⎝ ⎛⎭⎪⎫π4x ＋π4＋5(1≤x≤12，x ∈N *)D ．f(x)＝2sin ⎝ ⎛⎭⎪⎫π4x －π4＋5(1≤x≤12，x ∈N *)【答案】D【解析】根据题意，T ＝ 2(7－3)＝8，ω＝2πT ＝π4，由⎩⎪⎨⎪⎧A ＋B ＝7，－A ＋B ＝3， 得⎩⎪⎨⎪⎧A ＝2，B ＝5，当x ＝3时，2sin ⎝ ⎛⎭⎪⎫π4×3＋φ＋5＝7，得φ＝－π4.∴f(x)＝2sin ⎝ ⎛⎭⎪⎫π4x －π4＋5.故选D.4．一个大风车的半径为8，12旋转一周，它的最低点，离地面2，风车翼片的一个端点从开始按逆时针方向旋转，则点离地面距离与时间之间的函数关系式是（ ）m min 0P m P 0P P ()h m (min)tAC【答案】B5．为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针尖指向位置P(x ，y)．若初始位置为P0⎝⎛⎭⎪⎫32，12，秒针从P 0(注：此时t ＝0)开始沿顺时针方向走动，则点P 的纵坐标y 与时间t 的函数关系为( )A ．y ＝sin ⎝⎛⎭⎪⎫π30t ＋π6B ．y ＝sin ⎝ ⎛⎭⎪⎫－π60t －π6C ．y ＝sin ⎝ ⎛⎭⎪⎫－π30t ＋π6D ．y ＝sin ⎝ ⎛⎭⎪⎫－π30t －π6 【答案】C【解析】由题意，函数的周期为T ＝60，∴ω＝2π60＝π30.设函数解析式为y ＝sin ⎝ ⎛⎭⎪⎫－π30t ＋φ⎝ ⎛⎭⎪⎫0＜φ＜π2(秒针是顺时针走动)．∵初始位置为P 0⎝ ⎛⎭⎪⎫32，12，∴t ＝0时，y ＝12.∴sinφ＝12，φ可取π6.∴函数解析式为y ＝sin ⎝ ⎛⎭⎪⎫－π30t ＋π6.故选C.6．如图，质点P 在半径为2的圆周上逆时针运动，其初始位置为P 0(2，－2)，角速度为1，那么点P 到x 轴距离d 关于时间t 的函数图象大致为( )【答案】C7.已知某人的血压满足函数解析式f(t)＝24si n160πt ＋110.其中f(t)为血压(mmHg)，t 为时间(min)，则此人每分钟心跳的次数为( ) A ．60 B ．70 C ．80 D ．90 【答案】C【解析】由题意可得f ＝1T ＝160π2π＝80.所以此人每分钟心跳的次数为80.故选C.8.如图，某港口一天6时到18时的水深变化曲线近似满足函数y ＝3sin ⎝ ⎛⎭⎪⎫π6x ＋φ＋k.据此函数可知，这段时间水深(单位：m)的最大值为( )A ．5B ．6C ．8D ．10 【答案】C【解析】由图知－3＋k ＝2，k ＝5，y ＝3sin ⎝ ⎛⎭⎪⎫π6x ＋φ＋5，y max ＝3＋5＝8.故选C. 9. 【2017届福建省泉州市模拟三】海水受日月的引力，在一定的时候发生潮涨潮落，船只一般涨潮时进港卸货，落潮时出港航行，某船吃水深度（船底与水面距离）为米，安全间隙（船底与海底距离）为米，该船在开始卸货，吃水深度以米/小时的速度减少，该港口某季节每天几个时刻的水深如下表所示，若选择（）拟合该港口水深与时间的函数关系，则该船必须停止卸货驶离港口的时间大概控制在（要考虑船只驶出港口需要一定时间）A. 至B. 至C. 至D. 至 【答案】C10. 的部分图象如图所示，，则正确的选项是（ ）41.52:000.3()sin y A x K ωφ=++0,0A ω>>5:005:305:306:006:006:306:307:00()()00f x f =-AC【答案】A，解得，故选A ．11．已知函数向左平移个单位后，得到函数，下列关于的说法正确的是（ ） A BCD【答案】C 【解析】函数的图象向左平移A ，当时，．图象不关于点中心对称，∴A 不正确；对于B ，当时，，图象不关于轴对称，∴B 不正确；对于C ，的周期是．当时，函数取得最大值，01x =6π6π⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=32sin 62sin ππx x y 3π-=x 03sin ≠⎪⎭⎫⎝⎛-=πy ⎪⎭⎫ ⎝⎛0,3-π6π-=x 00sin ==y 6π-=x ⎪⎭⎫⎝⎛+=32sin πx y π12π=x 1211π-=xC正确；对于D，的周期是D不正确；故选：C．12.个单位，再向上平移个单位，得到的图象.若，且，则的最大值为（）A． B． C． D．【答案】C第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.某时钟的秒针端点A到中心O的距离为5 cm，秒针均匀地绕点O旋转，当时间t＝0时，点A与钟面上标12的点B重合，将A，B两点间的距离d()cm表示成t ()s的函数，则d＝_____________，其中t∈[]0，60.【答案】10sinπ60t.【解析】如图所示，OA＝OB＝5()cm，秒针由B均匀地旋转到A的时间为t()s，则∠AOB＝π30t，取AB中点为C，则OC⊥AB，从而∠AOC＝12∠AOB＝π60t.π1)(xg9)()(21=xgxg]2,2[,21ππ-∈xx212xx-625π635π1249π417π在Rt △AOC 中，AC ＝OAsin ∠AOC ＝5sin π60t ，∴d ＝AB ＝10sin π60t ，t ∈[]0，60.故填10sin π60t.14．某实验室一天的温度（单位： ）随时间（单位： ）的变化近似满足函数关系：，该实验室这一天的最大温差为__________．【答案】4【解析】 因为，所以，时，即时，函数取得最大值为，时，即时，函数取得最小值为，所以一天的最大温差为．15.已知某种交流电电流I(A)随时间t(s)的变化规律可以拟合为函数I ＝52sin ⎝ ⎛⎭⎪⎫100πt －π2，t ∈[0，＋∞)，则这种交流电在0.5 s 内往复运动的次数为________次． 【答案】25.【解析】∵f＝1T ＝ω2π＝100π2π＝50，∴0.5 s 内往复运动的次数为0.5×50＝25.故填25.16.某市的纬度是北纬21°34′，小王想在某住宅小区买房，该小区的楼高7层，每层3 m ，楼与楼之间相距15 m ，要使所买楼房在一年四季正午的太阳不被前面的楼房遮挡，最低应该选择第______层的房(地球上赤道南北各23°26′处的纬线分别叫南北回归线．冬季我国白天最短的一天冬至日太阳直射在南回归线上)． 【答案】3.三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17．画出函数y ＝|cosx|的图象并观察其周期．C t h [)0,24t ∈()102sin 123f t t ππ⎛⎫=-+⎪⎝⎭731233t ππππ<+<14t =()f t 10212+=2t =()f t 1028-=1284-=【答案】见解析.【解析】函数图象如图所示．从图中可以看出，函数y ＝|cosx|是以π为周期的波浪形曲线． 我们也可以这样进行验证：|cos(x ＋π)|＝|－cosx|＝|cosx|， 所以，函数y ＝|cosx|是以π为周期的函数．18.如图，某大风车的半径为2 m ，每12 s 旋转一周，它的最低点O 离地面0.5 m ．风车圆周上一点A 从最低点O 开始，运动t(s)后与地面的距离为h(m)．(1)求函数h ＝f(t)的关系式； (2)画出函数h ＝f(t)的图象．【答案】（1）y ＝－2cos πt 6＋2，h ＝f(t)＝－2cos πt6＋2.5.（2）见解析.【解析】(1)如图，以O 为原点，过点O 的圆O 1的切线为x 轴，建立直角坐标系，设点A 的坐标为(x ，y)，则h ＝y ＋0.5.设∠OO 1A ＝θ，则cosθ＝2－y2，y ＝－2cosθ＋2. 又θ＝2π12·t ＝πt6，所以y ＝－2cos πt 6＋2，h ＝f(t)＝－2cos πt6＋2.5.(2)列表：描点连线，即得函数h ＝－2cos 6t ＋2.5的图象如图所示：19. 以一年为一个周期调查某商品出厂价格及该商品在商店的销售价格时发现：该商品的出厂价格是在6元基础上按月份随正弦曲线波动的，已知3月份出厂价格最高为8元，7月份出厂价格最低为4元，而该商品在商店的销售价格是在8元基础上按月份随正弦曲线波动的，并已知5月份销售价最高为10元，9月份销售价最低为6元，假设某商店每月购进这种商品m 件，且当月售完，请估计哪个月盈利最大？并说明理由． 【答案】6月份盈利最大. 【解析】由已知条件可得，出厂价格函数关系式为 y 1＝2sin ⎝ ⎛⎭⎪⎫π4x －π4＋6，销售价格函数关系式为y 2＝2sin ⎝ ⎛⎭⎪⎫π4x －34π＋8，则利润函数关系式为 y ＝m(y 2－y 1)＝m[2sin ⎝ ⎛⎭⎪⎫π4x －34π＋8－2sin ⎝ ⎛⎭⎪⎫π4x －π4－6] ＝－22msin π4x ＋2m.当x ＝6时，y ＝2m ＋22m ＝(2＋22)m ， 即6月份盈利最大．20.设函数图像的一条对称轴是直线．（1）求并用“五点法”画出函数在区间上的图像； （2）求函数的单调增区间；【答案】（1（2【解析】（1)(),0( )2sin()(x f y x x f =<<-+=ϕπϕ8π=x ϕ)(x f y =],0[π)(x f y =故函数（221. 已知电流I 与时间t 的关系式为I=Asin(ωt+φ). (1)如图是I=Asin(ωt+φ),根据图中数据求解析式;(2)如果t ,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正上图像是在区间],0[)(πx f y =整数值是多少? 【答案】（1）（2）943. 【解析】试题分析：（1）由已知中函数的图象，我们可以分析出函数的最大值，最小值，周期及特殊点坐标，根据函数的解析式中参数与函数性质的关系，易得到函数的解析式．（2）由已知中如果tI能取到最大值和最小值, I=Asin(ωt+φ)的周期即可求解.(2)∵t I能取到最大值和最小值, ∴I=Asin(ωt+φ)的周期 ∴ω的最小正整数值是943.22. 弹簧挂着的小球作上下振动，时间t(s)与小球相对平衡位置(即静止时的位置)的高度h(cm)之间的函数关系式是h ＝2sin(2t －π4)， t ∈[0，＋∞)．(1)以t 为横坐标，h 为纵坐标，画出函数在长度为一个周期的闭区间上的简图； (2)小球开始振动的位置在哪里？(3)小球最高点、最低点的位置及各自距平衡位置的距离分别是多少？ (4)小球经过多长时间往复振动一次？ (5)小球1s 能振动多少次？【答案】（1）见解析；(2) 小球开始振动时的位置为(0，－2)(平衡位置的下方2cm 处)． （3）2cm ；（4）0.318次/s ．【解析】(1)画出h ＝2sin ⎝ ⎛⎭⎪⎫2t －π4的简图(长度为一个周期)．按五个关键点列表：描点并将它们用光滑的曲线连接起来，即得h ＝2sin ⎝⎛⎭⎪⎫2t －π4(t≥0)在一个周期的简图，如图所示．(2)t ＝0时，h ＝2sin ⎝ ⎛⎭⎪⎫－π4＝－2，即小球开始振动时的位置为(0，－2)(平衡位置的下方2cm处)．。

专题一坐标图像题识图、读图及用图表示化学变化规律的能力是近几年中考化学考查的主要能力之一，对这种能力的考查通常借助坐标图像题来完成。

解决此类问题必须注意以下两点：一是明确题目所描述的化学情景；二是看懂图像所描述的化学意义。

首先要搞清横、纵坐标表示的意义，然后分析相关变化过程，对图像涉及的量之间的关系进行分析，最后再判断各量之间的曲线变化关系与图像是否符合。

重点要抓住关键的三点(起点、折点、终点)、曲线的变化趋势及横、纵坐标的比例关系。

注：与溶解度曲线相关的坐标图像题分析详见P59。

类型一质量变化图像1．物质溶解时溶液中溶质质量的变化曲线(1)化学反应中反应物和生成物的质量变化图像酸、碱、盐溶液混合相互反应时，酸与碱的反应一般优先于该酸与盐的反应。

如：①向Na2CO3和NaOH的混合溶液中滴加稀HCl时，NaOH先和HCl发生中和反应，等NaOH被反应完后，Na2CO3才能和HCl反应放出CO2气体，生成气体的坐标曲线如图像⑤所示。

②向一定量的NaOH和Ba(NO3)2的混合溶液中逐滴加入稀硫酸时，稀硫酸能和氢氧化钠反应生成硫酸钠和水，硫酸钠能和硝酸钡反应生成硫酸钡沉淀，硫酸钡不溶于稀硝酸，因此能马上产生沉淀，当硝酸钡完全反应后，沉淀质量不再增大，生成沉淀的坐标曲线如图像③所示。

③向稀盐酸和FeCl3的混合溶液中滴加氢氧化钠溶液时，NaOH先和稀盐酸发生中和反应，当稀盐酸完全反应后，NaOH才能与FeCl3溶液反应生成沉淀，生成沉淀的坐标曲线如图像⑤所示。

同理，若溶液中有酸时，酸要完全反应后，才会出现CaCO3、BaCO3、Cu(OH)2等沉4(或Ag＋和Cl－)，则反应物一开始混合即有沉淀产淀；但是若反应物中分别含有Ba2＋和SO2－生。

(2)化学反应前后物质质量的变化曲线从反应曲线判断是酸加入碱还是碱加入酸：首先要根据图像起点pH的大小来判断起始溶液的酸碱性，然后根据曲线的走势和pH的变化确定加入溶液的酸碱性。

1.6 三角函数模型的简单应用一、选择题（每小题5分，共20分）1．电流强度I (A)随时间t (s)变化的关系式是I＝5sin(100πt ＋π3)，则当t ＝1200s 时，电流强度I为( )A ．5 AB ．2.5 AC ．2 AD ．－5 A 2．如图所示，一个单摆以OA 为始边，OB 为终边的角θ(－π<θ<π)与时间t (s)满足函数关系式θ＝12sin(2t ＋π2)，则当t ＝0时，角θ的大小及单摆频率是( )A.12，1π B ．2，1π C.12，π D ．2，π 3. 已知简谐运动f (x )＝2sin ⎝⎛⎭⎫π3x ＋φ(|φ|<π2)的图像经过点(0,1)，则该简谐运动的最小正周期T 和初相φ分别为( )A ．T ＝6，φ＝π6 B ．T ＝6，φ＝π3C ．T ＝6π，φ＝π6D ．T ＝6π，φ＝π34. 如图，设点A 是单位圆上的一定点，动点P 从点A 出发在圆上按逆时针方向旋转一周，点P 所旋转过的弧AP 的长为l ，弦AP 的长为d ，则函数d ＝f (l )的图象大致是( )二、填空题(每小题5分，共10分)5．某时钟的秒针端点A 到中心点O 的距离为5 cm ，秒针均匀地绕点O 旋转，当时间t ＝0时，点A 与钟面上标12的点B 重合．将A 、B 两点的距离d (cm)表示成t (s)的函数，则d ＝________，(其中t ∈[0,60])．6．据市场调查，某种商品一年内每件出厂价在7千元的基础上，按月呈f (x )＝A sin(ωx ＋φ)＋B (A >0，ω>0，|φ|<π2)的模型波动(x 为月份)，已知3月份达到最高价9千元，7月份价格最低为5千元，根据以上条件可确定f (x )的解析式为________．三、解答题(共70分)7．（15分）如图是一弹簧振子做简谐运动的图象，横轴表示振动的时间，纵轴表示振动的位移，求这个振子振动的函数解析式．8. （20分）一个被绳子牵着的小球做圆周运动(如图)．它从初始位置P 0开始，按逆时针方向以角速度ω rad/s 做圆周运动．已知绳子的长度为l ，求：(1)P 的纵坐标y 关于时间t 的函数解析式； (2)点P 的运动周期和频率；(3)如果ω＝π6 rad/s ，l ＝2，φ＝π4，试求y的最值；(4)在(3)中，试求小球到达x 轴的正半轴所需的时间．9．(20分) 在一个港口，相邻两次高潮发生时间相距12 h ，低潮时水的深度为8.4 m ，高潮时为16 m ，一次高潮发生在10月10日4∶00.每天涨潮落潮时，水的深度d (m)与时间t (h)近似满足关系式d ＝A sin(ωt ＋φ)＋h .(1)若从10月10日0∶00开始计算时间，选用一个三角函数来近似描述该港口的水深d (m)和时间t (h)之间的函数关系；(2)10月10日17∶00该港口水深约为多少？(保留一位小数)(3)10月10日这一天该港口共有多少时间水深低于10.3 m?10. （15分）已知某海滨浴场的海浪高度()y 米是时间(024,t t≤≤单位：h)的函数，记作()y f t =，下表是某日各时的浪高数据：t 03 6 9 12 15 18 2124 y1.51.00.51.01.51.00.50.991.5经长期观测，()y f t =的曲线可近似地看成是函数cos y A t b ω=+.(1)求函数cos y A t b ω=+的最小正周期T ，振幅A 及函数表达式；(2)依据规定：当海浪高度高于1米时才对冲浪爱好者开放，请依据(1)的结论，一天内的上午8:00时至晚上20:00时之间，有多少时间可供冲浪者进行运动？1.6 三角函数模型的简单应用答题纸得分：一、选择题题号 1 2 3 4答案二、填空题5． 6．三、解答题7.8.9.10.1.6 三角函数模型的简单应用 答案一、选择题1.B 解析：当t ＝1200 s 时，I ＝5sin(100π×1200＋π3)＝5cos π3＝2.5 A.2.A 解析：t ＝0时θ＝12sin π2＝12，由函数解析式易知单摆周期为2π2＝π，故频率为1π.3.A 解析： T ＝2πω＝2ππ3＝6，代入(0,1)点得sin φ＝12.∵－π2<φ<π2，∴φ＝π6.4.C 解析：令AP 所对圆心角为θ，由|OA |＝1，则l ＝θ，sin θ2＝d2，∴d ＝2sin θ2＝2sin l2，即d ＝f (l )＝2sin l2(0≤l ≤2π)，它的图象为C.二、填空题5. 10sin πt60解析： 如图，秒针每秒钟走10π60＝π6(cm)，∴L 弧AB ＝π6t (cm)，∴2θ＝πt 65＝πt30，∴θ＝πt 60，∴d AB ＝5×sin πt 60×2＝10sin πt 60.6. f (x )＝2sin(π4x －π4)＋7解析：由条件可知⎩⎪⎨⎪⎧A ＋B ＝9，－A ＋B ＝5，∴B ＝7，A ＝2.又T ＝2(7－3)＝8，∴ω＝π4，令3×π4＋φ＝π2， ∴φ＝－π4， ∴f (x )＝2sin(π4x －π4)＋7.三、解答题7.解： 设函数解析式为y ＝A sin(ωt ＋φ)，则A ＝2，由图象可知T ＝2×(0.5－0.1)＝45，∴ω＝2πT ＝5π2.∴5π2×0.1＋φ＝π2.∴φ＝π4. ∴函数的解析式为y ＝2sin(5π2t ＋π4)．8．解：(1)y ＝l sin(ωt ＋φ)，t ∈[0，＋∞)．(2)由解析式得，周期T ＝2πω，频率f ＝1T ＝ω2π. (3)将ω＝π6 rad/s ，l ＝2，φ＝π4代入解析式，得到y ＝2sin ⎝⎛⎭⎫π6t ＋π4，t ∈[0，＋∞)．最小正周期T ＝2πω＝2ππ6＝12.当t ＝12k ＋1.5，k ∈N 时，y max ＝2， 当t ＝12k ＋7.5，k ∈N 时，y min ＝－2.(4)设小球经过时间t 后到达x 轴正半轴， 令π6t ＋π4＝2π，得t ＝10.5， ∴当t ∈[0，＋∞)时，t ＝12k ＋10.5，k ∈N ，∴小球到达x 轴正半轴所需要的时间为10.5＋12k ，k ∈N .9. 解： (1)依题意知T ＝2πω＝12，故ω＝π6，h ＝8.4＋162＝12.2，A ＝16－12.2＝3.8，所以d ＝3.8sin(π6t ＋φ)＋12.2；又因为t ＝4时，d ＝16，所以sin(4π6＋φ)＝1，所以φ＝－π6，所以d ＝3.8sin(π6t －π6)＋12.2.(2)t ＝17时，d ＝3.8sin(17π6－π6)＋12.2＝3.8sin 2π3＋12.2≈15.5(m)．(3)令3.8sin(π6t －π6)＋12.2<10.3，有sin(π6t －π6)<－12，因此2k π＋7π6<π6t －π6<2k π＋116π(k ∈Z )，所以2k π＋4π3<π6t <2k π＋2π，k ∈Z ，所以12k ＋8<t <12k ＋12.令k ＝0，得t ∈(8,12)；令k ＝1，得t ∈(20,24)， 故这一天共有8小时水深低于10.3 m. 10. 解：(1)可得224T =，∴212T ωπ==，有6ωπ=，而振幅(1.50.5)20.5A =-÷=， ∴0.5cos 6y t b π=+，又当0t =时， 1.5y =，∴0.5cos0 1.5b +=，得1b =，∴0.5cos 16y t π=+；(2)由0.5cos 116t π+>，得cos 06t π>，∴22262k t k ππππ-<<π+，解得123123,k t k k -<<+∈Z ，而820t <<，取1k =，得915t <<， ∴可供冲浪者进行运动的时间为上午9:00时至下午15:00，共6小时.。

第一章三角函数三角函数．三角函数模型的简单应用
．了解曲线＝(ω＋φ)在物理上的应用，了解建立该类问题的数学模型所应掌握的物理知识．
．理解并掌握解数学应用问题的一般步骤，掌握将所发现的规律抽象为恰当的三角函数问题的方法，并能正确选择恰当的角作为变量建立函数关系．
三角函数模型的简单应用
．建立三角函数模型解决实际问题．
三角函数在数学中有着广泛的应用，在实际生活中也可以解决很多问题，如某天某段时间内温度的变化规律等．
如果某种现象的变化具有周期性，根据三角函数的性质，我们可以根据这一现象的特征和条件，利用三角函数知识构建数学模型，从而把这一具体现象转化为一个特定的数学模型——三角函数模型．
．解三角函数应用题的基本步骤．
第一步，阅读理解，审清题意．读题要做到逐字逐句，读懂题中的文字叙述，理解叙述所反映的实际背景，在此基础上，分析出已知什么，求什么，从中提炼出相应的数学问题．
第二步，搜集整理数据，建立数学模型．根据搜集到的数据，找出变化规律，运用已掌握的三角知识、物理知识以及其他相关知识建立关系式，在此基础上将实际问题转化为一个三角函数问题，实现问题的数学化，即建立三角函数模型．
第三步，利用所学的三角知识对得到的三角函数模型予以解答，求得结果．
第四步，将所得结论转译成实际问题的答案．
．下面是钱塘江某个码头今年春季每天的时间(单位：时)与水深(单位：米)的关系表：
时间时
水深米
请仔细观察表格中的数据，你能够从中得到一些什么信息？
分析：这是一道开放性试题，应该有多种不同答案．现将部分答案列举如下．。

1.6 三角函数模型的简单应用1.如图所示是一个简谐运动的图象,则下列判断正确的是()A.该质点的振动周期为0.7 sB.该质点的振幅为-5 cmC.该质点在0.1 s和0.5 s时的振动速度最大D.该质点在0.3 s和0.7 s时的位移为零解析:由题中图象及简谐运动的有关知识知,T=0.8 s,A=5 cm.当t=0.1 s或0.5 s时,v为零.答案:D2.函数y=cos x·|tan x|的大致图象是()解析:当-<x<0时,y=-sin x;当0<x<时,y=sin x;x=0时,y=0.象为选项C.答案:C3.如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针针尖位置P(x,y),若初始位置为P0,当秒针从P0(注:此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系为()A.y=sinB.y=sinC.y=sinD.y=sin解析:设y=sin(ωt+φ),其中ω<0.由=60,得|ω|=,∴ω=-.∴y=sin.又t=0时,y=,∴φ=.∴y=sin.答案:C4.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是()A.[0,1]B.[1,7]C.[7,12]D.[0,1]和[7,12]解析:由已知可得该函数的周期为T=12,ω=.又当t=0时,A,∴y=sin,t∈[0,12],可解得函数的单调递增区间是[0,1]和[7,12].答案:D5.据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈f(x)=A sin(ωx+φ)+b的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定f(x)的解析式为()A.f(x)=2sin+7(1≤x≤12,x∈N*)B.f(x)=9sin(1≤x≤12,x∈N*)C.f(x)=2sin x+7(1≤x≤12,x∈N*)D.f(x)=2sin+7(1≤x≤12,x∈N*)解析:令x=3,可排除D;令x=7,可排除B;由A==2,可排除C;由题意,可得A==2,b=7,周期T==2×(7-3)=8,∴ω=.于是f(x)=2sin+7,再代入点(3,9),结合φ的范围可求得φ=-.答案:A6.单摆从某点开始来回摆动,离开平衡位置O的距离s(cm)和时间t(s)的函数关系为s=3sin,那么单摆来回摆动的振幅和一次所需的时间分别为.解析:由题意知,单摆来回摆动的振幅A=3(cm),来回摆动一次的时间T==4(s).答案:3 cm,4 s7.电流强度I(A)随时间t(s)变化的关系式是I=5sin,则当t= s时,电流I为A.解析:当t= s时,I=5sin=5sin=5cos.答案:8.若函数f(x)=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且只有两个不同的交点,则k的取值范围是.解析:当x∈[0,π]时,sin x≥0,f(x)=3sin x;当x∈(π,2π]时,sin x≤0,f(x)=-sin x, 故函数f(x)的图象如下.若f(x)的图象与直线y=k有且只有两个不同的交点,则k∈(1,3).答案:(1,3)9.如图,弹簧上挂的小球做上下振动时,小球离开平衡位置的距离s(cm)随时间t(s)的变化曲线是一个三角函数的图象.(1)经过多长时间,小球往复振动一次?(2)求这条曲线的函数解析式;(3)小球在开始振动时,离开平衡位置的位移是多少?解:(1)由题中图象可知,周期T=2=π,所以小球往复振动一次所需要的时间为π≈3.14(s).(2)可设该曲线的函数解析式为s=A sin(ωt+φ)(A>0,ω>0,0≤φ<2π),t∈[0,+∞),从图象中可以看出A=4,T=2×=π.则=π,即ω=2,将t=,s=4代入解析式,得sin=1,解得φ=.所以这条曲线的函数解析式为s=4sin,t∈[0,+∞).(3)当t=0时,s=4sin =2(cm),故小球在开始振动时,离开平衡位置的位移是2 cm.10.已知某地一天从4时~16时的温度变化曲线近似满足函数y=10sin+20,x∈[4,16].(1)求该地区这一段时间内的温差;(2)若有一种细菌在15 ℃到25 ℃之间可以生存,那么在这段时间内,该细菌能生存多长时间? 解:(1)由函数易知,当x=14时函数取最大值,此时最高温度为30 ℃;当x=6时函数取最小值,此时最低温度为10 ℃,所以温差为30-10=20(℃).(2)∵4≤x≤16,∴x-,令15≤10sin+20≤25,∴-≤sin.∴-x-.∴≤x≤.∴该细菌的存活时间为(时).。