高考数学三角函数知识点总结及练习

高考三角函数知识点总结一、基本概念和性质1.弧度制：单位圆上的弧所对应的圆心角的大小定义为该弧的弧度。

1弧度等于圆周的1/2π。

2. 三角函数：正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)、余切函数cot(x)、正割函数sec(x)和余割函数csc(x)。

3.三角恒等式：包括同角三角恒等式、余角三角恒等式、反三角函数同角恒等式等。

4.周期性：正弦函数、余弦函数、正割函数和余割函数的周期都是2π；正切函数和余切函数的周期是π。

二、基本关系式1.正弦函数：在直角三角形中，正弦函数是指对于一个锐角三角形，三角形的对边和斜边的比值。

- sin(x) = a / c，其中a是对边，c是斜边。

- sin(x) = y / r，其中y是斜边在y轴上的投影，r是半径。

2.余弦函数：在直角三角形中，余弦函数是指对于一个锐角三角形，三角形的邻边和斜边的比值。

- cos(x) = b / c，其中b是邻边，c是斜边。

- cos(x) = x / r，其中x是斜边在x轴上的投影，r是半径。

3.正切函数：在直角三角形中，正切函数是指对于一个锐角三角形，三角形的对边和邻边的比值。

- tan(x) = a / b，其中a是对边，b是邻边。

- tan(x) = y / x，其中y是斜边在y轴上的投影，x是斜边在x轴上的投影。

4.余切函数：余切函数是正切函数的倒数。

- cot(x) = 1 / tan(x)。

5.正割函数：在直角三角形中，正割函数是指对于一个锐角三角形，三角形的斜边和邻边的比值的倒数。

- sec(x) = 1 / cos(x)。

6.余割函数：在直角三角形中，余割函数是指对于一个锐角三角形，三角形的斜边和对边的比值的倒数。

- csc(x) = 1 / sin(x)。

三、平面内角与弧度制之间的关系1.弧度制与度数之间的转换：-弧度=度数×π/180-度数=弧度×180/π2.弧度制下的角的性质：-一个圆上的圆心角的弧度数等于该弧所对应的弧的弧度数。

高中三角函数知识点归纳总结(通用10篇)高中数学三角函数知识点总结：三倍角公式篇一sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)高中数学三角函数知识点总结：三倍角公式推导篇二sin3a=sin(2a+a)=sin2acosa+cos2asina高中数学三角函数知识点总结：半角公式篇三tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)高中数学三角函数知识点总结：辅助角公式篇四Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t)，tant=A/B降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))高中数学三角函数知识点总结：和差化积篇五sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)高中三角函数知识点归纳篇六1.做高中数学题的时候千万不能怕难题！有很多人数学分数提不动，很大一部分原因是他们的畏惧心理。

三角函数知识点及题型归纳三角函数是数学中的一个重要分支，在几何、物理、工程等领域都有广泛的应用。

下面我们来详细归纳一下三角函数的知识点和常见题型。

一、三角函数的基本概念1、角的概念角可以分为正角、负角和零角。

按旋转方向，逆时针旋转形成的角为正角，顺时针旋转形成的角为负角，没有旋转的角为零角。

2、弧度制把长度等于半径长的弧所对的圆心角叫做 1 弧度的角。

用弧度作为单位来度量角的制度叫做弧度制。

弧度与角度的换算公式为：180°＝π 弧度。

3、任意角的三角函数设角α的终边上任意一点 P 的坐标为(x, y)，它与原点的距离为 r(r ＝√（x²＋ y²) ＞ 0)，则角α的正弦、余弦、正切分别为：sinα ＝ y/r，cosα ＝ x/r，tanα ＝ y/x（x ≠ 0）。

4、三角函数线有正弦线、余弦线、正切线，它们分别是角α的终边与单位圆交点的纵坐标、横坐标、纵坐标与横坐标的比值。

二、同角三角函数的基本关系1、平方关系：sin²α ＋cos²α ＝ 12、商数关系：tanα ＝sinα/cosα三、诱导公式诱导公式可以将任意角的三角函数转化为锐角的三角函数。

例如：sin(π ＋α) ＝sinα，cos(π α) ＝cosα 等。

四、三角函数的图象和性质1、正弦函数 y ＝ sin x图象：是一条波浪形曲线，周期为2π，对称轴为 x ＝kπ ＋π/2（k∈Z），对称中心为(kπ, 0)（k∈Z）。

性质：在π/2 ＋2kπ, π/2 ＋2kπ（k∈Z）上单调递增，在π/2 ＋2kπ, 3π/2 ＋2kπ（k∈Z）上单调递减。

2、余弦函数 y ＝ cos x图象：也是一条波浪形曲线，周期为2π，对称轴为 x ＝kπ（k∈Z），对称中心为(π/2 ＋kπ, 0)（k∈Z）。

性质：在π ＋2kπ, 2kπ（k∈Z）上单调递增，在2kπ, π ＋2kπ（k∈Z）上单调递减。

高考数学中的三角函数知识点概览数学是高考中的一门必修科目，而三角函数则是数学中重要的内容之一。

掌握好三角函数的知识点可以增加高考数学的成绩，本文将对高考数学中的三角函数知识点进行概览，帮助学生更好地备考。

1、三角函数的定义在平面直角坐标系中，通过将点P(x,y)沿x轴(或y轴，原点)作垂线得到点M(x,0)，点P与点M的连线与x轴的夹角为θ(0≤θ≤2π)，定义：(1)正弦函数(A是θ的集合)：f(θ)=sinθ=y/r(2)余弦函数(B是θ的集合)：f(θ)=cosθ=x/r(3)正切函数(C是θ的集合)：f(θ)=tanθ=y/x其中，r是点P到原点的距离，x和y分别是点P在x轴和y轴上的坐标。

2、基本性质(1)正弦函数和余弦函数的值域都是[-1,1]，而正切函数的定义域是整个实数集。

(2)正弦函数和余弦函数的图像是相似的，只是在垂直方向上有不同的偏移量。

(3)正弦函数和余弦函数的图像都是关于原点对称的。

(4)正切函数的图像是周期为π的函数，其图像是关于原点对称的。

(5)三角函数与三角恒等式有关，其中最常用的是：sin^2θ+cos^2θ=1tanθ=sinθ/cosθ3、三角函数的图像(1)正弦函数和余弦函数的图像在相同的坐标系中，画出正弦函数和余弦函数的图像，可以发现：正弦函数的图像是一条连续的波浪线，起伏在原点之上和之下。

它的周期是2π，在每个周期内，其最大值为1，在0、π、2π等点上取到；最小值为-1，在π/2、3π/2等点上取到。

余弦函数的图像与正弦函数的图像完全相似，只是在y轴上取值时，正弦函数是在原点上取到的，而余弦函数是在1和-1之间变化的。

它的周期也是2π，在每个周期内，其最大值为1，在π/2、3π/2等点上取到；最小值为-1，在0、π、2π等点上取到。

(2)正切函数的图像正切函数的图像是一条平移后的正弦函数图像。

其周期为π，其垂直渐近线为x=kπ（k∈Z），它的图像在x轴上有一个渐近点，在每个周期内，正切函数的值都在正无穷和负无穷之间变化。

三角函数一、根底学问定义1 角，一条射线围着它的端点旋转得到的图形叫做角。

若旋转方向为逆时针方向，则角为正角，若旋转方向为顺时针方向，则角为负角，若不旋转则为零角。

角的大小是随意的。

定义2 角度制，把一周角360等分，每一等价为一度，弧度制：把等于半径长的圆弧所对的圆心角叫做一弧度。

360度=2π弧度。

若圆心角的弧长为L ，则其弧度数的肯定值|α|=rL,其中r 是圆的半径。

定义3 三角函数，在直角坐标平面内，把角α的顶点放在原点，始边及x 轴的正半轴重合，在角的终边上随意取一个不同于原点的点P ，设它的坐标为（x ,y ），到原点的间隔 为r,则正弦函数s in α=ry,余弦函数co s α=rx,正切函数tan α=xy，余切函数cot α=y x ，定理1 同角三角函数的根本关系式， 倒数关系：tan α=,商数关系：tan α=；乘积关系：tan α×co s α=s in α,cot α×s in α=co s α；平方关系：s in 2α+co s 2α=1, tan 2α+1=se c 2α, cot 2α+1=c s c 2α. 定理2 诱导公式（Ⅰ）s in (α+π)=-s in α, co s(π+α)=-co s α, tan (π+α)=tan α;（Ⅱ）s in (-α)=-s in α, co s(-α)=co s α, tan (-α)=-tan α; （Ⅲ）s in (π-α)=s in α, co s(π-α)=-co s α, tan =(π-α)=-tan α; （ Ⅳ）s in =co s α, co s=s in α（奇变偶不变，符号看象限）。

定理3 正弦函数的性质，依据图象可得y =s inx （x ∈R ）的性质如下。

单调区间：在区间上为增函数，在区间上为减函数，最小正周期为2π. 奇偶数. 有界性：当且仅当x =2kx +2π时，y 取最大值1，当且仅当x =3k π-2π时, y 取最小值-1。

高考数学三角函数知识点总结及练习集团标准化小组：[VVOPPT-JOPP28-JPPTL98-LOPPNN]三角函数总结及统练一. 教学内容：三角函数总结及统练 （一）基础知识1. 与角α终边相同的角的集合},2{Z k k S ∈+==απβ2. 三角函数的定义（六种）——三角函数是x 、y 、r 三个量的比值3. 三角函数的符号——口诀：一正二弦，三切四余弦。

4. 三角函数线 正弦线MP=αsin 余弦线OM=αcos 正切线AT=αtan5. 同角三角函数的关系平方关系：商数关系：倒数关系：1cot tan =⋅αα 1csc sin =⋅αα 1sec cos =⋅αα 口诀：凑一拆一；切割化弦；化异为同。

6.正弦余弦正切 余切7. 8. 二倍角公式——代换：令αβ=降幂公式⎪⎪⎩⎪⎪⎨⎧+=-=22cos 1cos 22cos 1sin 22αααα半角公式：2cos 12sinαα-±=；2cos 12cos αα+±=；αααcos 1cos 12tan +-±= 函数图10. 函数)sin(ϕω+=x A y 的图象变换 0,0>>ωA函数)sin(ϕω+=x A y 的图象可以通过下列两种方式得到：（1）−−−−−−−−−→−+=−−−−→−=倍横坐标缩短到原来的图象左移ωϕϕ1)sin(sin x y x y（2）−−−−→−=−−−−−−−−−→−=ωϕωω图象左移倍横坐标缩短到原来的)sin(sin 1x y x y（二）数学思想与基本解题方法1. 式子变形原则：凑一拆一；切割化弦；化异为同。

2. 诱导公式原则：奇变偶不变，符号看象限。

3. 估用公式原则：一看角度，二看名称，三看特点。

4. 角的和与差的相对性如：)(βαβ+=－α 角的倍角与半角的相对性 如：422,22αααα==5. 升幂与降幂：升幂角减半，降幂角加倍。

6. 数形结合：心中有图，观图解题。

高考数学之三角函数知识点总结高考数学中，三角函数是一个重要的知识点。

它在解三角形、解三角方程和求极限等方面都有广泛应用。

下面是对高考数学中三角函数的知识点进行总结：一、基本概念和性质：1.三角函数的定义：正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数的定义。

2.三角函数的周期性：正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数的周期性。

3.三角函数的奇偶性：正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数的奇偶性。

4.三角函数的范围：正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数的范围。

二、基本公式和恒等变换：1.三角函数的和差化积公式。

2.三角函数的倍角公式。

3.三角函数的半角公式。

4.三角函数的和差化积公式的逆运算。

三、极坐标与三角函数：1.极坐标下的坐标转换。

2.极坐标下的两点间距离公式。

四、三角函数的解析式：1.任意角的解析式。

2.一些特殊角的解析式。

五、三角函数的图像与性质：1.正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数的图像和性质。

2.三角函数图像的平移、伸缩和翻转。

3.三角函数的性态。

六、三角函数的应用：1.三角函数在测量中的应用：测量高度、测量角度、计算地理位置等。

2.三角函数在力学中的应用：力的合成、平衡条件等。

3.三角函数在电路中的应用：交流电的正弦表达式等。

4.三角函数在几何中的应用：解三角形、求面积等。

5.三角函数在物理中的应用：波动现象、振动现象等。

以上是高考数学中三角函数的主要知识点总结。

掌握这些知识点，对于解答相关题目、理解相关概念都有很大帮助。

在备考高考数学时，应不断强化基础知识，多进行题目练习和真题训练，同时注重理解和巩固基本概念和性质，提高解题的能力和技巧。

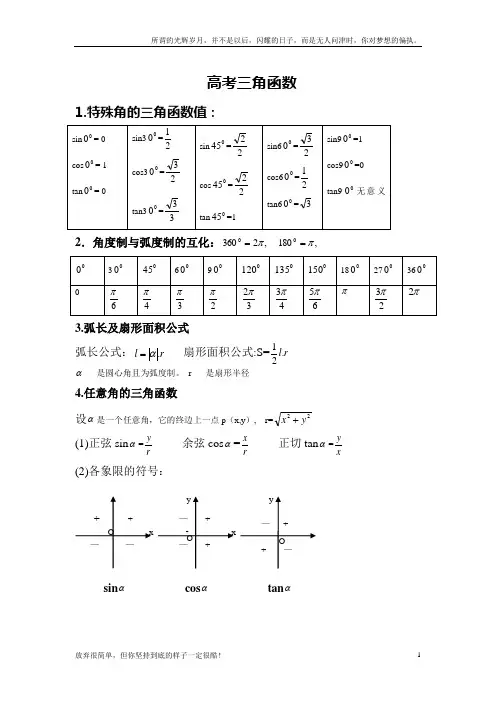
高考三角函数1.特殊角的三角函数值：2．角度制与弧度制的互化：,23600π= ,1800π=3.弧长及扇形面积公式弧长公式：r l .α= 扇形面积公式:S=r l .21α----是圆心角且为弧度制。

r-----是扇形半径4.任意角的三角函数设α是一个任意角，它的终边上一点p （x,y ）, r=22y x + (1)正弦sin α=r y 余弦cos α=r x 正切tan α=xy (2)各象限的符号：sin α cos α tan αxy+O— —+x yO — ++— +y O— ++ —5.同角三角函数的基本关系：（1）平方关系：s in 2α+ cos 2α=1。

（2）商数关系：ααcos sin =tan α （z k k ∈+≠,2ππα）6.诱导公式：记忆口诀：2k παα±把的三角函数化为的三角函数，概括为：奇变偶不变，符号看象限。

()()1sin 2sin k παα+=，()cos 2cos k παα+=，()()tan 2tan k k παα+=∈Z ． ()()2sin sin παα+=-，()cos cos παα+=-，()tan tan παα+=． ()()3sin sin αα-=-，()cos cos αα-=，()tan tan αα-=-． ()()4sin sin παα-=，()cos cos παα-=-，()tan tan παα-=-．口诀：函数名称不变，符号看象限．()5sin cos 2παα⎛⎫-=⎪⎝⎭，cos sin 2παα⎛⎫-= ⎪⎝⎭． ()6sin cos 2παα⎛⎫+= ⎪⎝⎭，cos sin 2παα⎛⎫+=- ⎪⎝⎭．口诀：正弦与余弦互换，符号看象限．7正弦函数、余弦函数和正切函数的图象与性质降幂公式： 1+cos α=2cos 22α cos 2α22cos 1α+=1-cos α=2sin 22αsin 2α22cos 1α-= 9．正弦定理 ：2sin sin sin a b cR A B C===. 余弦定理：2222cos a b c bc A =+-;2222cos b c a ca B =+-;2222cos c a b ab C =+-.三角形面积定理.111sin sin sin 222S ab C bc A ca B ===.1．直角三角形中各元素间的关系：如图，在△ABC 中，C ＝90°，AB ＝c ，AC ＝b ，BC ＝a 。

新高考三角函数知识点归纳总结三角函数在新高考数学考试中扮演着重要的角色。

掌握三角函数的相关知识点，不仅可以帮助我们解决各类与角度、长度及图形性质相关的问题，还能够为以后的高等数学学习打下坚实的基础。

本文将对新高考中的三角函数知识点进行归纳总结，以帮助同学们更好地复习和应对考试。

一、三角函数的基本概念和性质三角函数包括正弦函数、余弦函数和正切函数，它们都是角的函数，表示角与某一边的长度的比值。

1. 正弦函数（sin）：在直角三角形中，正弦值等于对边与斜边的比值，即sin(A) = a/c。

2. 余弦函数（cos）：在直角三角形中，余弦值等于邻边与斜边的比值，即cos(A) = b/c。

3. 正切函数（tan）：在直角三角形中，正切值等于对边与邻边的比值，即tan(A) = a/b。

此外，我们还需了解三角函数在单位圆上的定义和性质：4. 单位圆的角度：单位圆的半径为1，角度以弧度制表示，其中360°等于2π弧度。

5. 弧度与角度的转换关系：1弧度约等于57.3°，即1弧度≈ 57.3°。

6. 三角函数的周期性：正弦函数和余弦函数的周期为2π，而正切函数的周期为π。

二、三角函数的基本关系及推导1. 三角函数之间的基本关系：根据三角恒等式，我们可以推导出三角函数之间的基本关系。

例如，sin²A + cos²A = 1，tanA = sinA/cosA等。

2. 三角函数的和差化积公式：通过和差化积公式，我们可以将两个三角函数的和差表示为一个三角函数的乘积。

三、三角函数的图像和性质1. 正弦函数的图像和性质：正弦函数的图像是一条连续的波浪线，振幅为1，在0～2π的区间内周期性重复。

2. 余弦函数的图像和性质：余弦函数的图像也是一条连续的波浪线，振幅为1，在0～2π的区间内周期性重复，与正弦函数的图像相位差90°。

3. 正切函数的图像和性质：正切函数的图像有无数个渐近线，它在每个π的整数倍处有一个垂直渐近线，且在每个π/2的整数倍处有一个水平渐近线。

高考数学知识点：三角函数线（正弦线、余弦线、正切线）_知识点总结高考数学知识点：三角函数线（正弦线、余弦线、正切线）三角函数线的定义：设任意角α的顶点在原点O，始边与x轴的正半轴重合，终边与单位圆相交于点P（x，y），过P点作x轴的垂线，垂足为M，过点A（1，0）作单位圆的切线,高二，设它与角α的终边或其反向延长线相交于点T，则有向线段MP、OM，AT分别叫做角α的正弦线，余弦线，正切线，即：sinα=MP，cosα=OM，tanα=AT，如下图：注：线段长度表示三角函数值大小，线段方向表示三角函数值正负。

关于三角函数线，要注意以下几点：（1）正弦线、余弦线、正切线都是有向线段，利用它们的数量来表示三角函数值，是数形结合的典型体现。

三角函数线表示三角的函数值的符号规定如下：正弦线MP、正切线AT 方向与y轴平行，向上为正，向下为负；余弦线OM在x轴上，向右为正，向左为负。

（2）作三角函数线时，所用字母一般都是固定的，书写顺序也不能颠倒。

特别要注意正切线必在过A（1，0）的单位圆的切线上（其中二、三象限角需作终边的反向延长线）。

（3）对于终边在坐标轴上的角，有时三角函数线退化为一个点，有时又为整个半径。

当角α的终边在y轴上时，角α的正切线不存在。

（4）当时，正弦线、余弦线、正切线与角α并不是一一对应的。

一般地，每一个确定的MP、OM、AT都对应两个α的值。

诱导公式：公式一公式二公式三公式四公式五公式六规律：奇变偶不变，符号看象限。

即形如（2k+1）90°±α，则函数名称变为余名函数，正弦变余弦，余弦变正弦，正切变余切，余切变正切。

形如2k×90°±α，则函数名称不变。

诱导公式口诀“奇变偶不变，符号看象限”意义：的三角函数值．(1)当k为偶数时，等于α的同名三角函数值，前面加上一个把α看作锐角时原三角函数值的符号；(2)当k为奇数时，等于α的异名三角函数值，前面加上一个把α看作锐角时原三角函数值的符号。

三角函数核心内容一、角的概念的推广、弧度制●1．任意角：角是由射线绕端点旋转而成的，它有正角、负角与特殊的零角。

●2．终边相同的角：所有与角α终边相同的角，连同角α在内，称为终边相同的角，记为{360,}S k k Z ββα==+⋅∈o●3．象限角：把角置于直角坐标系中，使角的顶点与坐标原点重合，角的始边与x 轴的正半轴重合，那么角的终边落在第几象限，我们就说这个角是第几象限角。

例如：第二象限角的集合：{36090360180,}S k k k Z αα=⋅︒+︒<<⋅︒+︒∈●4．坐标轴上的角终边在x 轴上的角的集合：{180,}S k k Z αα==⋅︒∈ 终边在y 轴上的角的集合：{18090,}S k k Z αα==⋅︒+︒∈ 终边在坐标轴上的角的集合：{90,}S k k Z αα==⋅︒∈ ●5．角的度量：弧度制，角度制。

1rad 角：弧长与圆半径长相等的弧所对的圆心角的大小称为1rad 角。

弧度和角度的换算：180()rad π︒=10.01745180rad rad π︒=≈1801()()57.305718rad π'=︒≈︒=︒●6．弧长和扇形面积公式 l R α=⋅ 21122S l R R α=⋅=⋅二、任意角的三角函数●1．任意角的三角函数的定义：设点(,)P x y 是角α终边上一点，点O 是坐标原点，22||r OP x y ==+，那么角α的正弦、余弦、正切分别是sin ,cos ,tan (0)y yx x r r xααα===≠。

●2．三角函数值的符号：正弦、余弦、正切函数值在各象限的符号是： ＋＋－－xy ＋－－ ＋xy ＋－＋ －xyOOO●3．三角函数线：正弦线sin MP α=，余弦线cos OM α=，正切线tan AT α=。

三、同角三角函数的基本关系式与诱导公式●1．同角三角函数的基本关系式，注意公式的变形使用。

（1）22sin cos 1αα+= （2）sin tan cos ααα= ●2．诱导公式：与角“32,,,,22k πππααπααα+-±±±”有关的诱导公式的记忆口诀是“奇变偶不变, 符号看象限”。

高中数学三角函数复习专题一、知识点整理 :1、角的看法的推行：正负，范围，象限角，坐标轴上的角；2、角的会集的表示：①终边为一射线的角的会集：x x2k, k Z=|k 360o, k Z②终边为向来线的角的会集：x x k, k Z；③两射线介定的地域上的角的会集：x 2k x2k, k Z④两直线介定的地域上的角的会集：x k x k, k Z；3、任意角的三角函数：（1）弧长公式： l a R R 为圆弧的半径，a为圆心角弧度数， l 为弧长。

（2）扇形的面积公式：S 1lR R 为圆弧的半径， l 为弧长。

2（3）三角函数定义：角中边上任意一点 P 为 ( x, y) ，设 | OP |r 则：sin y, cos x ,tan y r= a 2b2 r r x反过来，角的终边上到原点的距离为r 的点P的坐标可写为：P r cos, r sin 比如：公式 cos()cos cossin sin的证明（4）特别角的三角函数值α032 64322sin α012310-10222cosα13210-101222tan α0313不存不存0 3在在（5）三角函数符号规律：第一象限全正，二正三切四余弦。

（6）三角函数线：（判断正负、比较大小，解方程或不等式等）y T 如图，角的终边与单位圆交于点P，过点 P 作 x 轴的垂线，P 垂足为 M ，则Ao 过点 A(1,0)作 x 轴的切线，交角终边OP 于点 T，则M x。

（7）同角三角函数关系式：①倒数关系： tana cot a 1sin a ②商数关系： tan acosa③平方关系： sin 2 a cos2 a1（ 8)引诱公试sin cos tan三角函数值等于的同名三角函数值，前方-- sin+ cos- tan加上一个把看作锐角时，原三角函数值的- tan-+ sin- cos符号；即：函数名不变，符号看象限+- sin- cos+ tan2-- sin+ cos- tan2k++ sin+ cos+ tansin con tan2+ cos+ sin+ cot三角函数值等于的异名三角函数值，前方2+ cos- sin- cot加上一个把看作锐角时，原三角函数值的3- cos- sin+ cot2符号 ;3- cos+ sin- cot2即：函数名改变，符号看象限 : sin x cos x cos x比方444cos x sin x444.两角和与差的三角函数：（1）两角和与差公式：cos() cos a cos sin a sin sin( a) sin a coscosa sintan a(atan a tan注：公式的逆用也许变形)1 tan a tan．．．．．．．．．（2）二倍角公式：sin 2a 2sin acosa cos 2a cos2 a sin 2 a12 sin2 a 2 cos2 a 12 tan atan 2a1 tan2 a(3)几个派生公式：①辅助角公式：a sinx bcosx a2b2 sin(x)a22 cos()b x比方： sinα± cosα＝ 2 sin4＝ 2 cos4．sinα±3 cosα＝ 2sin3＝2cos3等．②降次公式： (sin cos) 21sin 2cos21cos2,sin 21cos222③ tan tan tan()(1 tan tan)5、三角函数的图像和性质：（此中 k z ）三角函数y sin x定义域（- ∞， +∞）值域[-1,1]最小正周期T2奇偶性奇[ 2k,2k]22单调性单调递加[ 2k,2k3 ]22单调递减x k对称性2(k ,0)零值点x ky cosx（- ∞， +∞）[-1,1]T 2偶[( 2k 1) ,2k ]单调递加[( 2k , (2k 1) ]单调递减x k(k,0)2x k2y tan xx k2（-∞，+∞）T奇(k,k)22单调递加k(,0)x kx k2x 2 k，最值点y max1ymax 1；无x k2x(2k 1) ，y min1y min1 6、 .函数y Asin( x) 的图像与性质：（本节知识观察一般能化成形如y Asin( x) 图像及性质）（ 1）函数 y Asin( x) 和 y Acos( x2 ) 的周期都是T（ 2）函数y A tan( x) 和 y Acot( x) 的周期都是T（ 3）五点法作y Asin( x) 的简图，设t x，取0、、、3、2来求相应x22的值以及对应的y 值再描点作图。

高中数学三角函数知识点总结高中数学三角函数知识点总结一、锐角三角函数公式sin=的对边/斜边cos=的邻边/斜边tan=的对边/的邻边cot=的邻边/的对边二、倍角公式Sin2A=2SinA?CosACos2A=CosA2-SinA2=1-2SinA2=2CosA2-1tan2A=(2tanA)/(1-tanA2)(注：SinA2是sinA的平方sin2(A))三、三倍角公式sin3=4sinsin(/3+)sin(/3-)cos3=4coscos(/3+)cos(/3-)tan3a=tanatan(/3+a)tan(/3-a)三倍角公式推导sin3a=sin(2a+a)辅助角公式Asin+Bcos=(A2+B2)(1/2)sin(+t)，其中sint=B/(A2+B2)(1/2)cost=A/(A2+B2)(1/2)tant=B/AAsin+Bcos=(A2+B2)(1/2)cos(-t)，tant=A/B 四、降幂公式sin2=(1-cos(2))/2=versin(2)/2cos2=(1+cos(2))/2=covers(2)/2tan2=(1-cos(2))/(1+cos(2))推导公式tan+cot=2/sin2tan-cot=-2cot21+cos2=2cos21-cos2=2sin21+sin=(sin/2+cos/2)2=2sina(1-sina)+(1-2sina)sina=3sina-4sinacos3a=cos(2a+a)=(2cosa-1)cosa-2(1-sina)cosa=4cosa-3cosasin3a=3sina-4sina=4sina(3/4-sina)=4sina[(3/2)-sina]=4sina(sin60-sina)=4sina(sin60+sina)(sin60-sina)=4sina*2sin[(60+a)/2]cos[(60-a)/2]*2sin[(60-a)/2]cos[(60-a)/2]=4sinasin(60+a)sin(60-a)cos3a=4cosa-3cosa=4cosa(cosa-3/4)=4cosa[cosa-(3/2)]=4cosa(cosa-cos30)=4cosa(cosa+cos30)(cosa-cos30)=4cosa*2cos[(a+30)/2]cos[(a-30)/2]*{-2sin[(a+30)/2]sin[(a-30)/2]}=-4cosasin(a+30)sin(a-30)=-4cosasin[90-(60-a)]sin[-90+(60+a)]=-4cosacos(60-a)[-cos(60+a)]=4cosacos(60-a)cos(60+a)上述两式相比可得tan3a=tanatan(60-a)tan(60+a)五、半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin2(a/2)=(1-cos(a))/2cos2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))六、三角和sin(++)=sincoscos+cossincos+coscossin-sinsinsincos(++)=coscoscos-cossinsin-sincossin-sinsincos tan(++)=(tan+tan+tan-tantantan)/(1-tantan-tantan-tantan)七、两角和差cos(+)=coscos-sinsincos(-)=coscos+sinsinsin=sincoscossintan(+)=(tan+tan)/(1-tantan)tan(-)=(tan-tan)/(1+tantan)八、和差化积sin+sin=2sin[(+)/2]cos[(-)/2]sin-sin=2cos[(+)/2]sin[(-)/2]cos+cos=2cos[(+)/2]cos[(-)/2]cos-cos=-2sin[(+)/2]sin[(-)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 九、积化和差sinsin=[cos(-)-cos(+)]/2coscos=[cos(+)+cos(-)]/2sincos=[sin(+)+sin(-)]/2cossin=[sin(+)-sin(-)]/2十、诱导公式sin(-)=-sincos(-)=costan(—a)=-tansin(/2-)=coscos(/2-)=sinsin(/2+)=coscos(/2+)=-sinsin(-)=sincos(-)=-cossin(+)=-sincos(+)=-costanA=sinA/cosAtan(/2+)=-cottan(/2-)=cottan(-)=-tantan(+)=tan诱导公式记背窍门：奇变偶不变，符号看象限十一、万能公式sin=2tan(/2)/[1+tan(/2)]cos=[1-tan(/2)]/1+tan(/2)]tan=2tan(/2)/[1-tan(/2)]十二、其它公式(1)(sin)2+(cos)2=1(2)1+(tan)2=(sec)2(3)1+(cot)2=(csc)2(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=-Ctan(A+B)=tan(-C)(tanA+tanB)/(1-tanAtanB)=(tan-tanC)/(1+tantanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=n(nZ)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot( C/2)(7)(cosA)2+(cosB)2+(cosC)2=1-2cosAcosBcosC(8)(sinA)2+(sinB)2+(sinC)2=2+2cosAcosBcosC(9)sin+sin(+2/n)+sin(+2*2/n)+sin(+2*3/n)++sin[+2*( n-1)/n]=0cos+cos(+2/n)+cos(+2*2/n)+cos(+2*3/n)++cos[+2*(n-1)/n]=0以及sin2+sin2(-2/3)+sin2(+2/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0拓展阅读：学好函数的方法一、学数学就像玩游戏，想玩好游戏，当然先要熟悉游戏规那么而在数学当中，游戏规那么就是所谓的根本定义。

完整版)高三三角函数专题复习(题型全面)三角函数考点1：三角函数的概念三角函数是以角度或弧度为自变量的函数，包括正弦函数、余弦函数、正切函数等。

考点2：三角恒等变换三角恒等变换包括两角和、差公式、倍角半角公式、诱导公式、同角的三角函数关系式等。

考点3：正弦函数、余弦函数、正切函数的图像和性质正弦函数、余弦函数、正切函数的定义域、值域、最值、单调区间、最小正周期、对称轴对称中心等性质都需要掌握。

考点4：函数y=Asin(x)(A,)的图像与性质函数y=Asin(x)(A,)的定义域、值域、最值、单调区间、最小正周期、对称轴对称中心等性质也需要掌握。

此外，该函数的图像还可以通过一定的变换得到。

一、三角函数求值问题1.三角函数的概念例1.若角的终边经过点P(4a,3a)(a0)，则sin=-3/5.2.公式法例2.设(0,π/2)，若sin=1/2，则2cos()=√3.练1.已知角的终边上一点的坐标为（sinθ。

cosθ）(θ∈(π/2,π))，则sin=-cosθ。

3.化简求值例3.已知为第二象限角，且sin=15/17，求sin(+π/4)的值。

练：1.已知sin=1/5，则sin4-cos4的值为-24/25.2.已知tan(θ+)=1/2，求tanθ和sin2θ-cosθ.sinθ+2cos2θ的值。

4.配凑求值例4．已知,∈(π/3,π/2)，且sin(+)=-√3/2，sin(-)=1/2，求cos(+)的值。

练：1.设α∈(π/12,π/3)，β∈(0,π/6)，且sin(α+β)=-√3/2，sin(β-α)=-1/2，则cos(α+β)=1/2.1.已知三角函数的值，求其他三角函数的值已知 $sin\alpha = \frac{4}{5}$，$cos\beta = \frac{3}{5}$，$cos(\alpha - \beta) = \frac{1}{2}$，$sin(\beta + \theta) =\frac{3}{5}$，求 $sin(\alpha + \beta)$ 和 $tan(\alpha - 2\beta)$。

――概念、方法、题型、易误点及应试技巧总结三角函数1、角的概念的推广：平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。

按逆时针方向旋转所形成的角叫正角，按顺时针方向旋转所形成的角叫负角，一条射线没有作任何旋转时，称它形成一个零角。

射线的起始位置称为始边，终止位置称为终边。

2、象限角的概念：在直角坐标系中，使角的顶点与原点重合，角的始边与x 轴的非负半轴重合，角的终边在第几象限，就说这个角是第几象限的角。

如果角的终边在坐标轴上，就认为这个角不属于任何象限。

3. 终边相同的角的表示：（1）α终边与θ终边相同(α的终边在θ终边所在射线上)⇔2()k k αθπ=+∈Z ，注意：相等的角的终边一定相同，终边相同的角不一定相等.如与角 1825-的终边相同，且绝对值最小的角的度数是＿＿＿，合＿＿＿弧度。

（答：25-；536π-）（2）α终边与θ终边共线(α的终边在θ终边所在直线上) ⇔()k k αθπ=+∈Z . （3）α终边与θ终边关于x 轴对称⇔2()k k αθπ=-+∈Z . （4）α终边与θ终边关于y 轴对称⇔2()k k απθπ=-+∈Z . （5）α终边与θ终边关于原点对称⇔2()k k απθπ=++∈Z .（6）α终边在x 轴上的角可表示为：,k k Z απ=∈；α终边在y 轴上的角可表示为：,2k k Z παπ=+∈；α终边在坐标轴上的角可表示为：,2k k Z πα=∈.如α的终边与6π的终边关于直线x y =对称，则α＝____________。

（答：Z k k ∈+,32ππ）4、α与2α的终边关系：由“两等分各象限、一二三四”确定.如若α是第二象限角，则2α是第_____象限角 （答：一、三）5.弧长公式：||l R α=，扇形面积公式：211||22S lR R α==，1弧度(1rad)57.3≈. 如已知扇形AOB 的周长是6cm ，该扇形的中心角是1弧度，求该扇形的面积。

三角函数例题和知识点总结三角函数是数学中一个重要的分支，在解决几何、物理等问题中有着广泛的应用。

下面我们将通过一些例题来深入理解三角函数的知识点。

一、三角函数的基本概念三角函数包括正弦函数（sin）、余弦函数（cos）、正切函数（tan）等。

在直角三角形中，正弦函数定义为对边与斜边的比值，余弦函数定义为邻边与斜边的比值，正切函数定义为对边与邻边的比值。

例如，一个直角三角形的一个锐角为θ，对边为 a，邻边为 b，斜边为 c，则sinθ ＝ a/c，cosθ ＝ b/c，tanθ ＝ a/b。

二、特殊角的三角函数值我们需要牢记一些特殊角（如 0°、30°、45°、60°、90°）的三角函数值。

｜角度｜ 0°｜ 30°｜ 45°｜ 60°｜ 90°｜｜｜｜｜｜｜｜｜ sin ｜ 0 ｜ 1/2 ｜√2/2 ｜√3/2 ｜ 1 ｜｜ cos ｜ 1 ｜√3/2 ｜√2/2 ｜ 1/2 ｜ 0 ｜｜ tan ｜ 0 ｜√3/3 ｜ 1 ｜√3 ｜不存在｜三、三角函数的诱导公式诱导公式用于将任意角的三角函数转化为锐角的三角函数。

例如，sin(180° α) ＝sinα，cos(180° α) ＝cosα 等。

四、三角函数的图像和性质1、正弦函数 y ＝ sin x 的图像是一个周期为2π 的波浪线，其值域为-1, 1，在0, 2π内，函数在 x ＝π/2 处取得最大值 1，在 x ＝3π/2 处取得最小值－1。

2、余弦函数 y ＝ cos x 的图像也是一个周期为2π的波浪线，值域为-1, 1，在0, 2π内，函数在 x ＝ 0 处取得最大值 1，在 x ＝π 处取得最小值－1。

五、例题解析例 1：已知sinα ＝ 1/2，且α为锐角，求α的度数和cosα的值。

因为sinα ＝ 1/2，且α为锐角，所以α ＝ 30°。

三角函数知识点归纳总结高三高三数学中的三角函数知识点归纳总结在高三数学中，三角函数是一个重要的知识点，它是解析几何、微积分等学科的基础。

三角函数的内容较为繁杂，但只要掌握了基本的公式和性质，就能够顺利地解决各种问题。

以下是对高三数学中三角函数知识点的归纳总结。

1. 三角函数的定义三角函数是指正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数这六种函数。

其中，正弦函数和余弦函数的定义域为实数集，其余函数的定义域为实数集减去相应函数零点的集合。

2. 基本公式和性质(1) 正弦函数和余弦函数的基本周期为2π，即sin(x+2π)=sinx，cos(x+2π)=cosx。

(2) 正切函数和余切函数的基本周期为π，即tan(x+π)=tanx，cot(x+π)=cotx。

(3) 正弦函数和余弦函数的和差公式：sin(x±y) = sinxcosy ± cosxsiny，cos(x±y) = cosxcosy ∓ sinxsiny。

(4) 正切函数和余切函数的和差公式：tan(x±y) = (tanx ±tany)/(1∓tanxtany)，cot(x±y) = (c otxcoty∓1)/(coty∓cotx)。

(5) 正切函数和余切函数的互余公式：tanx=cot(π/2−x)，cotx=tan(π/2−x)。

(6) 三角函数的奇偶性：sin(-x)=-sinx，cos(-x)=cosx，tan(-x)=-tanx，cot(-x)=-cotx。

(7) 三角函数的周期性：有些三角函数的周期不是基本周期2π或π，而是它们的倍数，如sin3x和cos3x的周期为2π/3。

3. 三角函数的图像(1) 正弦函数和余弦函数的图像：它们的图像都是周期性的波形，正弦函数的图像在坐标系的x轴正半轴上方，余弦函数的图像在坐标系中x轴上。

(2) 正切函数和余切函数的图像：它们的图像分别是以x轴和y轴为渐近线的一组双曲线。