定义 位移边界条件
§2-6 边界条件
边界条件 --表示在边界上位移与约 束,或应力与面力之间的关系。
位移边界条件 --设在su部分边界
上给定位移分量 u (s) 和 v(s) ,则有
(u)s u(s), (v)s v(s), (在 su上)。(2-14)
第二章 平面应力问题和平面应变问题
位移边界条件的说明:
第二章 平面应力问题和平面应变问题
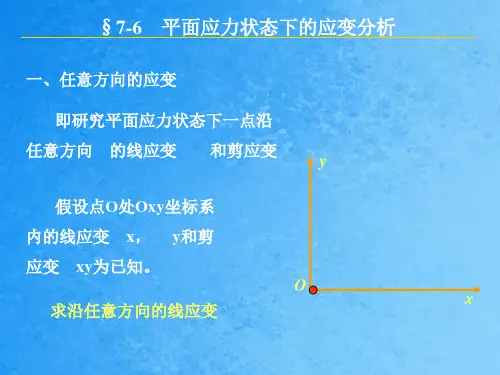
斜面应力
(3)求主应力
设某一斜面为主面,则只有 σn σ, τn 0, 由此建立方程,求出:
σmax x y
σ min
2
tan 1
σ σ
1
2
xy
.
x
2
y
2
2 xy
,
(2-6)
第二章 平面应力问题和平面应变问题
平行xy面,柱体非常长;
故任何z 面(截面)均为对称面。
w 0, 只有u,v; (平面位移问题)
w 0 εz 0,
τzx, τzy 0 zx, zy 0,
只有 x , y , xy .
(平面应变问题)
第二章 平面应力问题和平面应变问题
平面应变
(2)由于截面形状、体力、面力及约束沿
故其物理方程为:
x
1 E
σx σ y
y
1 E
σy
σx
xy
21
E
xy
(2 12)
第二章 平面应力问题和平面应变问题
定义
对平面应变问题,由于 zy 0, zx 0