实验二 驻波分布特性的测量与分析

驻波演示实验报告驻波演示实验报告引言：驻波是波动现象中的一种特殊情况，它在各个科学领域都有广泛的应用。

为了更好地理解和研究驻波的特性，我们进行了一次驻波演示实验。

本报告将详细介绍实验的目的、原理、实验装置和实验结果。

目的：本次实验的主要目的是通过驻波演示实验，加深对驻波现象的理解，并观察驻波在不同条件下的特性变化。

同时，通过实验数据的分析，验证驻波的基本原理和公式。

原理：驻波是由两个同频率、同振幅的波在相反方向上传播时产生的干涉现象。

在实验中，我们使用了一根弦作为传播介质，通过在弦上施加不同频率的激励波，使其在弦上形成驻波。

实验装置：实验装置包括一根细长的弦、激励器和测量仪器。

首先，将弦固定在两个固定点之间，保持其紧绷状态。

然后，将激励器与弦连接，通过调节激励器的频率和振幅，产生不同的激励波。

最后，使用测量仪器，如频率计和振幅计，对驻波进行测量和记录。

实验过程：在实验开始之前，我们首先调整弦的紧绷度，确保弦的振动不受松紧程度的影响。

然后，通过改变激励器的频率，我们逐步找到弦上出现驻波的条件。

一旦驻波形成，我们使用频率计测量驻波的频率，并使用振幅计测量驻波的振幅。

实验结果：通过实验，我们观察到了驻波的几个重要特性。

首先，我们发现驻波的频率与激励波的频率相等，这与驻波的基本原理相符。

其次，我们注意到驻波的振幅随着激励波的振幅的增加而增加，这表明驻波的振幅与激励波的振幅有直接的关系。

最后，我们观察到在一定条件下，驻波的波节和波腹位置保持不变，这与驻波的空间分布特性相符。

讨论与分析：通过对实验结果的分析，我们可以得出以下结论：驻波的频率与激励波的频率相等，这是驻波形成的必要条件；驻波的振幅与激励波的振幅有直接的关系，振幅越大，驻波的振幅也越大；驻波的波节和波腹位置保持不变，这是驻波的空间分布特性。

这些结论与驻波的基本原理相吻合，验证了实验的有效性。

结论：通过驻波演示实验，我们更深入地了解了驻波现象的特性和原理。

弦线上的驻波实验实验报告实验目的：本实验的目的是通过弦线上的驻波实验，探究驻波的特性及其与弦线长度、振动频率和弦张力的关系。

同时，通过实验观察驻波现象，进一步理解波动的基本原理。

实验原理：驻波是指两个相同频率、振幅相等且沿相反方向传播的波相遇后在同一空间内定向干涉而形成的波动现象。

在弦线上，当两个反向传播的波相遇时，由于波在相接处的叠加，会产生节点和腹部。

节点是波的振动幅度为零的位置，腹部则是波的振动幅度最大的位置。

驻波的性质与弦线的长度、振动频率和弦张力密切相关。

根据弦线的特性，我们可以通过改变弦线的长度、振动频率和弦张力来观察驻波的变化情况。

实验步骤：1.准备实验装置，将一根细弦拴在平直的固定支架上，并通过转动装置与信号发生器连接。

2.设置信号发生器的频率为初始频率，并调整输出幅度使得弦线振幅合适，避免过大过小。

3.轻轻触碰弦线使其产生波动，并观察弦线上是否出现驻波现象。

如果出现驻波，继续调整信号发生器的频率，观察驻波的变化情况。

4.测量弦线上节点（振幅为零的点）的位置，并记录下来。

5.根据测得的节点位置，计算波长，并进一步计算弦线的线密度。

6.固定弦线一端的支架，并用一物体调整弦线的长度。

重复步骤3-5，记录下不同弦线长度下的节点位置，并计算波长。

7.固定弦线长度不变，调整信号发生器的频率，重复步骤3-5，记录下不同频率下的节点位置，并计算波长。

8.固定弦线长度和频率，逐渐调整弦线的张力，重复步骤3-5，记录下不同张力下的节点位置，并计算波长。

实验结果：在本次驻波实验中，我们通过改变弦线的长度、振动频率和弦张力，观察了驻波的变化情况，并记录了节点的位置，计算了波长。

实验讨论：根据实验结果可以得出以下结论：1.当弦线的长度改变时，驻波的节点位置也会发生相应的改变。

节点的位置与弦线长度成正比，即弦线长度越短，节点位置越靠近振动源。

2.频率的变化也会导致驻波节点位置的变化。

频率越大，节点位置越靠近振动源。

驻波实验报告
驻波是指在一定条件下，波在空间中形成固定的幅度分布和相位分布的现象。

在本次实验中，我们将通过实验数据和分析，探讨驻波的产生条件、特点以及应用。

首先，我们在实验室中搭建了一个驻波实验装置，利用信号发生器产生一定频
率的波源，波经过一定长度的传播路径后，被反射回来与原波相叠加形成驻波。

我们通过调节信号发生器的频率和改变传播路径的长度，观察并记录下了一系列的实验数据。

实验结果显示，当传播路径的长度为波长的整数倍时，驻波的节点和腹部位置
固定不变，形成稳定的驻波现象。

而当传播路径的长度不满足整数倍关系时，驻波现象将不会出现，波将继续传播而不形成驻波。

进一步分析实验数据，我们发现驻波的节点处波的振幅为零，而腹部位置波的
振幅达到最大值。

这说明在驻波中，波的振幅分布是固定的，而相位分布则呈现周期性变化。

这是驻波的一个重要特点，也是我们通过实验所观察到的现象。

在实际应用中，驻波现象被广泛应用于各种领域。

例如，在乐器制作中，驻波
的产生和控制对于提高乐器的音质和音色起着至关重要的作用。

此外，在无线通信领域，驻波的产生和传播特性也对天线设计和信号传输起着重要的影响。

总的来说，驻波是一种重要的波现象，通过本次实验，我们对驻波的产生条件、特点以及应用有了更深入的了解。

希望通过今后的学习和实践，能够进一步探索驻波的更多奥秘，并将其应用于更多的实际问题中。

实验2 研究弦线上的驻波现象一、实验目的1.观察弦线上驻波的变化，了解并熟悉实验仪器的调整方法。

2.研究弦线振动时的振动频率与振幅变化对形成驻波的影响。

波长与张力的关系；3.在弦线张力不变时，研究弦线振动时驻波波长与振动频率的关系。

4.改变弦线张力后，研究弦线振动时驻波波长与振动频率的关系。

二、仪器和用具可调频率的数显机械振动源、弦线支撑平台、固定滑轮、可调滑轮、砝码盘、米尺、弦线、砝码、频闪灯、分析天平等。

见图2-1图2-1 仪器结构图1.可调频率数显机械振动源2.振簧片3.弦线4.可动刀口支架5.可动滑轮支架6.标尺7.固定滑轮8.砝码与砝码盘9.变压器10.实验平台11.实验桌三、实验原理在一根拉紧的弦线上，其中张力为T，线密度为 ，则沿弦线传播的横波应满足下述运动方程：2222xy T t y ∂∂=∂∂μ (2-1)式中x 为波在传播方向（与弦线平行）的位置坐标，y 为振动位移。

将(2-1)式与典型的波动方程 22222x y V t y ∂∂=∂∂相比较，即可得到波的传播速度: μTV =若波源的振动频率为f ，横波波长为λ，由于λf V =，故波长与张力及线密度之间的关系为：μλT f 1= (2-2)为了用实验证明公式(2-2)成立，将该式两边取对数，得：f T log log 21log 21log --=μλ 若固定频率f 及线密度μ，而改变张力T ，并测出各相应波长λ，作log λ-log T 图，若得一直线，计算其斜率值（如为21），则证明了λ∝21T 的关系成立。

同理，固定线密度μ及张力T ，改变振动频率f ，测出各相应波长λ，作log λ-log f 图，如得到斜率为-1的直线则验证了λ∝f -1。

弦线上的波长可利用驻波原理测量。

当两个振幅和频率相同的相干波在同一直线上相向传播时，其所叠加而成的波称为驻波，一维驻波是波干涉中的一种特殊情形。

在弦线上出现许多静止点，称为驻波的波节，相邻两波节间的距离为半个波长。

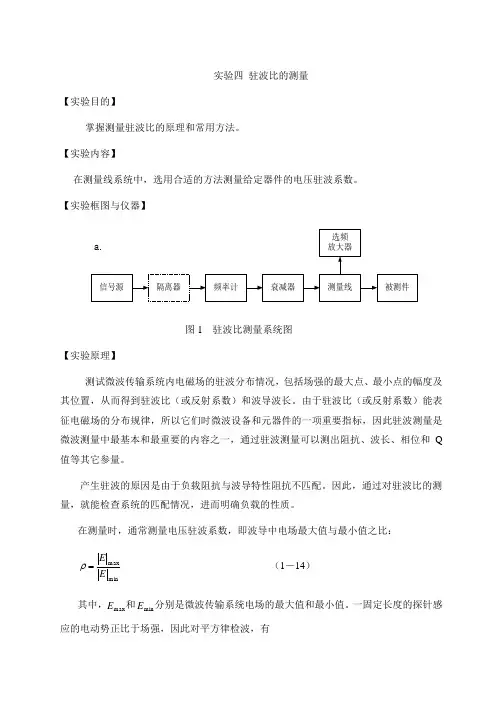
实验四 驻波比的测量【实验目的】掌握测量驻波比的原理和常用方法。

【实验内容】在测量线系统中，选用合适的方法测量给定器件的电压驻波系数。

【实验框图与仪器】网络分析仪被测件信号源被测件频谱仪b. c.图1 驻波比测量系统图 【实验原理】测试微波传输系统内电磁场的驻波分布情况，包括场强的最大点、最小点的幅度及其位置，从而得到驻波比（或反射系数）和波导波长。

由于驻波比（或反射系数）能表征电磁场的分布规律，所以它们时微波设备和元器件的一项重要指标，因此驻波测量是微波测量中最基本和最重要的内容之一，通过驻波测量可以测出阻抗、波长、相位和Q 值等其它参量。

产生驻波的原因是由于负载阻抗与波导特性阻抗不匹配。

因此，通过对驻波比的测量，就能检查系统的匹配情况，进而明确负载的性质。

在测量时，通常测量电压驻波系数，即波导中电场最大值与最小值之比：minmax E E =ρ （1－14）其中，max E 和min E 分别是微波传输系统电场的最大值和最小值。

一固定长度的探针感应的电动势正比于场强，因此对平方律检波，有式中，m ax I 和m in I 分别是电场为最大和最小时指示器的读数。

对于直线律检波有m inm axI I =ρ （1－16） 如果不知道检波律，必须用晶体检波特性曲线求出场强和指示器读数的关系再求得)151(minmax min max-==I I E E ρminmax min maxI I E E ==ρ （1－2）一般都是在小信号状态下进行测量，为此检波晶体二极管都是工作在平方律检波区域（检波电流I ∝E 2），故应有：minmaxI I =ρ当电压驻波系数在1.05<ρ<1.5时，驻波的最大值和最小值相差不大，且不尖锐，不易测准，为了提高测量准确度，可采用节点偏移法。

节点偏移法测量驻波比的测试系统如图5示。

测量方法：逐点改变短路活塞的位置（读数S ），在测量线上用交叉读数法跟踪测得某一波节点的位置（读数为D ），作出S 和（D+S ）+KS 的关系曲线，其中121-=λλK ,1λ是取下待测元件，固定短路活塞位置，移动测量线探针测得的测量线中的波长；2λ是固定测量探针，移动短路活塞，用交叉读数法在短路活塞上测得的波长。

物理实验“驻波（二）”改进班级：姓名：学号：在进行实验“驻波（二）（实验目的为了解纵驻波的形成并测定空气中的声速）”过程中，我发现该实验存在以下不足并想到可能有效的方法：1)该实验目的中有了解纵驻波的形成，而实验过程中没有形象体现。

我们难以确定空气注重形成几处波腹和波节改进方法：我在改进实验中添加了一个微型麦克风，并连接电脑，使得同学可以绘制出空气柱中驻波的大致图形.这样同学不仅可以定性地知道驻波在空气柱中形成，同时可以从绘制出的驻波图形中定量地掌握驻波相关方面的知识，并且利用“驻波”法来测量声速。

）2)测定空气中的声速时，声源用的是音叉。

一个同学用软锤敲击音叉，另一个同学控制蓄水桶下移，听轰鸣声（三处）来记录水面位置d1、d2、d3。

①由于会有一段高度都会听到强的轰鸣声，人很难分辨什么时候是最强的，记录时会产生较大误差；②敲击玻璃管上方的音叉，敲一下，自己能在几秒内听到声音，再敲打，则难以分清是共振还是被敲击的声音，使记录点难以确定；改进方法：我将接收声音信号的微型麦克风接入电脑，在电脑屏幕上有具体的体现，可以清楚的判断声音强弱。

而且我用小喇叭替换音叉，使声频一定，音量一定，更利于分别。

③记录时，控制蓄水桶的同学手会颤动，影响数据的记录；改进方法：我加入了漏斗，橡皮管等装置，在步骤5中先大致确定范围，在步骤6控制水面，进行测量。

这样可以固定并准确的控制水面高度，同时利于读数。

④实验过程中，随着敲击音叉和移动蓄水桶致使玻璃管内水面的移动的同时进行，会产生多普勒效应，效果不理想；改进方法：我将微型麦克风设置成可人为移动，在实验进行过程中随水面移动，可避免多普勒效应⑤玻璃管内为无色的水，记录刻度时同样不明显；改进方法：我在实验中，将红墨水滴入玻璃仪器中，使共鸣管中液体颜色与玻璃颜色区分，利于读数。

改进后实验：实验器材：共鸣管、温度计、毫米刻度尺、记号笔、红墨水、橡皮管、折型玻璃管、木塞、水槽、止水夹、漏斗、滴管、铁架、微型麦克风、小喇叭、电脑实验原理：1)前进的横波和其反射波叠加可产生横驻波，同样，前进的纵波和其反射波叠加可产生纵驻波。

THANKS
感谢观看
示波器
用于观察信号波形，以便调整 实验参数。
传感器
用于测量实验中的物理量，如 位移、速度等。
实验操作流程
信号源设置
根据实验需求设置信号源的频 率和幅度。
数据采集
启动信号源，通过示波器观察 信号波形，同时使用传感器测 量物理量，记录数据。
实验前准备
检查实验设备是否完好，确保 实验环境安全。
传感器安装
问题。
理论解释
结合理论对实验结果进行解释， 加深对驻波的理解和认识。
实际应用
探讨驻波在实际应用中的可能性 ，如声学、振动等领域。
04
CATALOGUE
驻波法实验的优缺点
优点
原理简单
驻波法基于简单的物理原理，使得实验易于理解 。
操作方便
驻波法实验设备相对简单，操作过程也较为方便 。
结果直观
通过观察驻波的形成和变化，可以直观地理解波 动现象。
03
CATALOGUE
驻波法实验结果与讨论
实验结果展示
波形图
通过实验测量，得到的驻 波波形图显示了波节和波 腹的位置和振幅变化。
频率与波长
通过测量得到的波形图， 可以计算出对应的频率和 波长，验证了驻波的特性 。
相位差
实验中观察到不同位置的 振动相位存在差异，证明 了驻波的相位差特性。
结果分析
02
研究驻波法的适用范围，尝试将其应用于更广泛的波动问题。
引入现代技术
03
结合现代科技，如传感器、计算机控制等，提升驻波法实验的
ቤተ መጻሕፍቲ ባይዱ
自动化和智能化水平。
05
CATALOGUE
驻波法实验案例分析

大学物理驻波实验报告大学物理驻波实验报告引言：驻波是物理学中一个重要的现象，它在很多领域都有广泛的应用。

本次实验旨在通过观察和测量驻波的特性，深入了解驻波现象及其相关的物理原理。

实验目的：1. 理解驻波的定义和基本特性；2. 学习使用仪器测量驻波的参数；3. 掌握驻波的数学表达式及其物理解释。

实验原理：驻波是由两个同频率、同振幅的相向传播的波叠加形成的。

当两个波相遇时，它们会相互干涉，形成驻波。

在一维情况下，驻波的表达式为y(x, t) = 2Asin(kx)sin(ωt)，其中A为振幅，k为波数，x为位置，ω为角频率。

实验装置：1. 信号发生器：用于产生驻波的信号；2. 波形发生器：用于产生驻波所需的波形；3. 波形显示器：用于观察和测量驻波的参数；4. 测量工具：如尺子、计时器等。

实验步骤：1. 将信号发生器和波形发生器连接，并设置相同的频率和振幅；2. 将波形发生器的输出连接到波形显示器，并调整显示器的位置和角度，以便观察到驻波的现象；3. 通过调节波形发生器的相位差，观察驻波的变化，并记录下相应的数据；4. 使用尺子测量波形显示器上相邻两个节点（波峰或波谷）之间的距离，并记录下来；5. 重复步骤3和步骤4，直到获得足够的数据。

实验结果与分析：通过实验观察和测量，我们得到了一系列驻波的数据。

根据这些数据，我们可以计算出驻波的波长、频率和相速度等参数。

首先，我们可以通过测量相邻两个节点之间的距离来计算驻波的波长。

根据驻波的定义，相邻两个节点之间的距离应该等于波长的一半。

因此，我们可以将测得的距离乘以2，得到驻波的波长。

其次，我们可以通过测量信号发生器的频率和波长，计算出驻波的频率。

根据频率的定义，频率等于波速除以波长。

由于我们已经测得了波长，所以可以将波速除以波长，得到驻波的频率。

最后，我们可以通过测量两个相邻节点之间的时间间隔，计算出驻波的相速度。

相速度定义为波长除以周期。

由于周期等于时间间隔的倒数，所以可以将波长除以时间间隔，得到驻波的相速度。

实验二驻波分布特性的测量与分析一、实验目的（1）了解测量线调整和使用方法；（2）测量观察测量线终端不同负载(短路、开路、匹配)时，测量系统的驻波分布情况；（3）理解在矩形波导系统中，不同终端负载对传输系统状态的影响。

二、实验原理当波导中存在不均匀性或负载不匹配时，波导中存在驻波。

测量驻波特性的仪器为测量线。

测量线通常由一段开槽传输线(如开槽波导)、探头座（耦合探针、探针的调谐腔体）和输出指示表、传动装置三部分组成。

测量线为了从波导中拾取能量，需要把探针伸入波导，由此在波导中引入不均匀性，从而影响测量系统的正常工作状态。

为了分析方便，通常将探针等效为与传输线并联的导纳Y p=g p+j b p ,其中g p 反映探针吸取功率的大小，b p表示探针在波导中产生反射的影响。

在信号源和波导系统匹配的情况下，当终端接任意阻抗负载时，由于g p 的分流作用，驻波波腹点的电场强度比真实值小。

而b p 的存在将使驻波波腹点和波节点的位置发生变化。

当终端为短路时，由于此时驻波波节点处的输入导纳为Y in→∞ ，所以Y p 不起作用，故驻波节点位置不会发生偏移。

然而在驻波波幅点，Y p影响就特别显著，尤其是探针容性电纳b p的存在，将使驻波波幅点向负载方向偏移，造成测量误差。

为了减少g p 的影响可以适当减少探针插入深度，b p的消除则要依靠探针的调谐电路来达到。

实验中测量线探针电路的调整一般包括调节探针深度和调节指针调谐滑塞(即耦合输出匹配电路)。

探针插入适当的深度通常为 1.0~1.5mm。

当测量系统终端短路时，将探针移至两个驻波波节点正中间位置(即波腹点位置)，调节指针调谐滑塞，直至在选频放大器上观察到的指示最大，此时b p的影响减至最小。

调谐的过程就是减少探针反射对驻波图形的影响和提高测量系统灵敏度的过程，这是减少驻波测量误差的关键，必须认真调整。

当改变信号源频率或者探针深度时，由于探针电纳Y p亦相应改变，必须对探针电路重新进行调整。

实验目的：1、观察弦振动及驻波的形成；3、在振动源频率不变时，用实验确定驻波波长与张力的关系；4、在弦线张力不变时，用实验确定驻波波长与振动频率的关系；4、定量测定某一恒定波源的振动频率；5、学习对数作图法。

实验仪器：弦线上驻波实验仪（FD-FEW-II型）包括：可调频率的数显机械振动源、平台、固定滑轮、可动刀口、可动卡口、米尺、弦线、砝码等；分析天平，米尺。

实验原理：如果有两列波满足：振幅相等、振动方向相同、频率相同、有固定相位差的条件，当它们相向传播时，两列波便产生干涉。

一些相隔半波长的点，振动减弱最大，振幅为零，称为波节。

两相邻波节的中间一点振幅最大，称为波腹。

其它各点的振幅各不相同，但振动步调却完全一致，所以波动就显得没有传播，这种波叫做驻波。

驻波相邻波节间的距离等于波长λ的一半。

如果把弦线一端固定在振动簧片上，并将弦线张紧，簧片振动时带动弦线由左向右振动，形成沿弦线传播的横波。

若此波前进过程中遇到阻碍，便会反射回来，当弦线两固定端间距为半波长整数倍时，反射波与前进波便形成稳定的驻波。

波长λ、频率f和波速V满足关系：V = fλ (1)又因在张紧的弦线上，波的传播速度V与弦线张力T及弦的线密度μ有如下关系：(2)比较(1)、(2)式得：(3)为了用实验证明公式(3)成立，将该式两边取自然对数，得：(4)若固定频率f及线密度μ，而改变张力T，并测出各相应波长λ ，作ln T -lnλ图，若直线的斜率值近似为，则证明了的关系成立。

同理，固定线密度μ及张力T，改变振动频率f，测出各相应波长λ，作ln f - lnλ图，如得一斜率为的直线就验证了。

将公式(3)变形，可得：(5)实验中测出λ、T、μ的值，利用公式（5）可以定量计算出f的值。

实验时，测得多个(n个)半波长的距离l，可求得波长λ为：(6)为砝码盘和盘上所挂砝码的总重量；用米尺测出弦线的长度L，用分析天平测其质量，求出弦的线密度（单位长度的质量）：(7)实验内容：1、验证横波的波长λ与弦线中的张力T 的关系（f不变）固定波源振动的频率，在砝码盘上添加不同质量的砝码，以改变同一弦上的张力。

驻波实验报告篇一：驻波实验报告实验目的：1、观察弦振动及驻波的形成；3、在振动源频率不变时，用实验确定驻波波长与张力的关系；4、在弦线张力不变时，用实验确定驻波波长与振动频率的关系；4、定量测定某一恒定波源的振动频率；5、学习对数作图法。

实验仪器：弦线上驻波实验仪（FD-FEW-II型）包括：可调频率的数显机械振动源、平台、固定滑轮、可动刀口、可动卡口、米尺、弦线、砝码等；分析天平，米尺。

实验原理：如果有两列波满足：振幅相等、振动方向相同、频率相同、有固定相位差的条件，当它们相向传播时，两列波便产生干涉。

一些相隔半波长的点，振动减弱最大，振幅为零，称为波节。

两相邻波节的中间一点振幅最大，称为波腹。

其它各点的振幅各不相同，但振动步调却完全一致，所以波动就显得没有传播，这种波叫做驻波。

驻波相邻波节间的距离等于波长λ的一半。

如果把弦线一端固定在振动簧片上，并将弦线张紧，簧片振动时带动弦线由左向右振动，形成沿弦线传播的横波。

若此波前进过程中遇到阻碍，便会反射回来，当弦线两固定端间距为半波长整数倍时，反射波与前进波便形成稳定的驻波。

波长λ、频率 f和波速V满足关系：V = f λ(1)又因在张紧的弦线上，波的传播速度V 与弦线张力T及弦的线密度μ有如下关系：(2)比较(1)、(2)式得：(3) 为了用实验证明公式(3)成立，将该式两边取自然对数，得：(4)若固定频率f 及线密度μ，而改变张力T，并测出各相应波长λ，作lnT -lnλ图，若直线的斜率值近似为，则证明了的关系成立。

同理，固定线密度μ及张力T，改变振动频率f，测出各相应波长λ，作ln f - lnλ图，如得一斜率为的直线就验证了。

将公式(3)变形，可得：(5) 实验中测出λ、T、μ的值，利用公式（5）可以定量计算出 f 的值。

实验时，测得多个(n个)半波长的距离l，可求得波长λ为：(6)为砝码盘和盘上所挂砝码的总重量；用米尺测出弦线的长度L，用分析天平测其质量，求出弦的线密度（单位长度的质量）：(7)实验内容：1、验证横波的波长λ与弦线中的张力T 的关系（f 不变）固定波源振动的频率，在砝码盘上添加不同质量的砝码，以改变同一弦上的张力。

中国科大六系微波与天线实验室版权所有实验二驻波分布特性的测量微波与天线实验室实验指导幻灯片中国科大六系微波与天线实验室版权所有中国科大六系微波与天线实验室版权所有实验目的•了解测量线的调整和使用方法；•通过测量观察测量线终端接不同负载（短路、开口、匹配负载）时系统中形成的驻波分布情况;•掌握用直读法测量负载驻波比的方法。

微波与天线实验室实验指导幻灯片中国科大六系微波与天线实验室版权所有中国科大六系微波与天线实验室版权所有实验原理•测量线调整▪→探针伸入波导内引入不均匀性→等效：p p p jb g Y +=gp 反映探针吸取功率的大小bp 反映探什在波导中产生反射的影响gp端接任意负载时→ gp 分流，驻波波腹点电场强度比真实值小;bp 会使驻波波腹点和波节点位置发生变化;微波与天线实验室实验指导幻灯片中国科大六系微波与天线实验室版权所有中国科大六系微波与天线实验室版权所有实验原理(续)•终端短路→波节点处Yin →∞ →波节位置不会偏移•终端短路→波腹点处Yp 影响明显→波节位置因探针容性电纳bp 的存在→驻波波腹点向负载方向p 偏移•减小Yp 的影响→：适当减少探针插入深度;p gp bp：调整探针的调谐电路；微波与天线实验室实验指导幻灯片中国科大六系微波与天线实验室版权所有中国科大六系微波与天线实验室版权所有实验原理(续)•调整方法：10~15mm 探针深度：1.0~1.5mm 终端短路→探针移至波腹位置→调节测量线上的调谐活塞→选放指示最大→OK ！•注意事项：频率改变，调谐要重新进行！微波与天线实验室实验指导幻灯片中国科大六系微波与天线实验室版权所有中国科大六系微波与天线实验室版权所有实验原理(续)•驻波分布：终端短路测量线终端接短路板终端短路：测量线终端接短路板→纯驻波分布终端开口：测量线终端开口→终端匹配：测量线终端接匹配负载→行波分布注意事项终端开口与开路的区别•注意事项：终端开口与开路的区别微波与天线实验室实验指导幻灯片中国科大六系微波与天线实验室版权所有中国科大六系微波与天线实验室版权所有实验原理(续)•驻波分布测量方法测量线终端接待测负载→移动测量线探针→按一定方式记录探针位置和检波指示值（d~i ）→描绘驻波分布特性图形微波与天线实验室实验指导幻灯片中国科大六系微波与天线实验室版权所有中国科大六系微波与天线实验室版权所有实验原理(续)•驻波分布测量方法测量数据要求:至少包括两个波节点,三个波腹点,且相邻波节和波腹点之间测量点不得少于4个;注:匹配负载情况下根据实际观测量适当数据点;微波与天线实验室实验指导幻灯片中国科大六系微波与天线实验室版权所有中国科大六系微波与天线实验室版权所有实验原理(续)•驻波比的测量驻波比（ρ,s)：描述驻波分布状态的重要参数；小信号工作，平方律检波条件下，实验中可由如下公式得到驻波比I 和I i 分别是驻波波腹点和波节点的检波电流min max I I S=Imax和Imin分别是驻波波腹点和波节点的检波电流值。

物理驻波实验报告物理驻波实验报告引言：驻波是物理学中一个重要的现象，它在许多领域中都有广泛的应用。

本实验旨在通过驻波实验，探究驻波的形成原理、特性以及相关的物理量测量方法。

实验装置：本次实验采用的装置是一条绳子，两端固定在两个支架上。

实验中，我们通过手持绳子的一端，以一定频率振动绳子，观察并测量驻波的形成和特性。

实验步骤：1. 将绳子两端固定在支架上，确保绳子保持水平。

2. 用手持绳子的一端，以一定频率振动绳子。

3. 观察绳子上形成的驻波，并记录下观察到的现象。

4. 测量驻波的波长和频率。

实验结果：通过实验观察和测量，我们得到了以下结果：1. 驻波的形成：当我们以一定频率振动绳子时，产生的波向绳子的另一端传播，并在两端发生反射。

当传播波与反射波相遇时，它们叠加形成了驻波。

驻波的形成是由于传播波和反射波之间的干涉效应。

2. 驻波的节点和腹部：在驻波中，存在一些固定的位置，这些位置上的振动幅度为零，称为节点。

而在节点之间的位置上，振动幅度达到最大值，称为腹部。

3. 驻波的波长：通过测量绳子上相邻两个节点的距离，我们可以得到驻波的波长。

实验结果表明，驻波的波长是传播波长的两倍。

4. 驻波的频率：通过测量绳子振动的频率，我们可以得到驻波的频率。

实验结果表明，驻波的频率与传播波的频率相同。

实验分析：通过以上实验结果，我们可以得出以下结论：1. 驻波是由传播波和反射波之间的干涉效应形成的。

2. 驻波的节点和腹部位置是固定的，它们的位置与波长有关。

3. 驻波的波长是传播波长的两倍，频率与传播波的频率相同。

实验应用：驻波现象在许多领域中都有广泛的应用，例如：1. 乐器制作：驻波的特性可以用于调整乐器的音质和音高。

2. 声波传输：驻波可以用于声波在管道中的传输和扩散控制。

3. 振动测量：通过驻波的形成和特性，可以测量振动频率和波长，从而得到物体的振动状态。

结论：通过本次实验，我们深入了解了驻波的形成原理、特性以及相关的物理量测量方法。

试验二驻波的测量《微波技术与天线》实验指导书主编赵霞审核楚栓成校对杨艺北方民族大学电气信息工程学院二○○八年三月目录实验系统介绍 (3)实验一微波测量系统 (9)实验二驻波的测量 (12)实验三阻抗及匹配 (15)实验四微波技术应用的研究 (18)实验系统简介微波技术是近代发展起来的一门尖端科学技术，它不仅在通讯、原子能技术、空间技术、量子电子学以及农业生产等方面有着广泛的应用，在科学研究中也是一种重要的观测手段，微波的研究方法和测试设备都与无线电波的不同。

从图1可以看出，微波的频率范围是处于光波和广播电视所采用的无线电波之间，因此它兼有两者的性质，却又区别于两者。

与无线电波相比，微波有下述几个主要特点图1 电磁波的分类1．波长短(1m —1mm)：具有直线传播的特性，利用这个特点，就能在微波波段制成方向性极好的天线系统，也可以收到地面和宇宙空间各种物体反射回来的微弱信号，从而确定物体的方位和距离，为雷达定位、导航等领域提供了广阔的应用。

2．频率高：微波的电磁振荡周期(10-9一10-12s)很短，已经和电子管中电子在电极间的飞越时间(约10-9s)可以比拟，甚至还小，因此普通电子管不能再用作微波器件(振荡器、放大器和检波器)中，而必须采用原理完全不同的微波电子管(速调管、磁控管和行波管等)、微波固体器件和量子器件来代替。

另外，微波传输线、微波元件和微波测量设备的线度与波长具有相近的数量级，在导体中传播时趋肤效应和辐射变得十分严重，一般无线电元件如电阻，电容，电感等元件都不再适用，也必须用原理完全不同的微波元件(波导管、波导元件、谐振腔等)来代替。

3．微波在研究方法上不像无线电那样去研究电路中的电压和电流，而是研究微波系统中的电磁场，以波长、功率、驻波系数等作为基本测量参量。

4．量子特性：在微波波段，电磁波每个量子的能量范围大约是10-6～10-3eV，而许多原子和分子发射和吸收的电磁波的波长也正好处在微波波段内。

一、实验目的1. 观察在两端被固定的弦线上形成的驻波现象；2. 了解弦线达到共振和形成稳定驻波的条件；3. 测定弦线上横波的传播速度；4. 确定弦线作受迫振动时的共振频率与驻波波长、张力和弦线线密度之间的关系。

二、实验原理1. 横波的波速：横波沿弦线传播时，在维持弦线张力不变的情况下，横波的传播速度v与张力FT及弦线的线密度（单位长度的质量）l之间的关系为：v =√(FT/l)。

2. 驻波的形成：考虑两列振幅、频率相同，有固定相位差，传播方向相反的间谐波u1(x, t) = Acos(kx - ωt)和u2(x, t) = A cos(kx + ωt)。

其中k为波数，ω为角频率，u1与u2之间的相位差为2π，叠加后的合成运动为：u(x, t) =u1(x, t) + u2(x, t) = 2Acos(kx)cos(ωt)。

3. 驻波的特性：由上可知，时间和空间部分是分离的，某个x点振幅不随时间改变，振幅最大的点称为波腹，振幅为零的点为波节。

上述运动状态为驻波。

驻波中振动的相位取决于cos(kx/2)因子的正负，它每经过波节变号一次。

三、实验仪器1. 弦音计装置一套（包括驱动线圈和探测器线圈各一个，1Kg砝码和不同密度的吉他线，信号发生器，数字示波器，千分尺，米尺）。

四、实验步骤1. 将吉他线一端固定在支架上，另一端连接驱动线圈，驱动线圈与信号发生器相连。

2. 将探测器线圈放置在弦线上，用于检测驻波。

3. 调整信号发生器的频率，观察示波器上的波形变化。

4. 改变弦线的张力，重复步骤3，观察驻波的变化。

5. 改变弦线的线密度，重复步骤3，观察驻波的变化。

6. 记录不同条件下驻波的频率、波长、振幅等数据。

五、实验结果与分析1. 驻波的形成：通过实验观察，当驱动线圈振动时，弦线上形成了一系列驻波。

在弦线两端固定的条件下，驻波呈现出波腹和波节的分布。

2. 驻波的频率与波长的关系：根据实验数据，可以得出驻波的频率f与波长λ之间的关系为f = v/λ，其中v为弦线上横波的传播速度。

实验二驻波分布特性的测量实验目的◆了解测量线的调整和使用方法◆通过测量观察测量线终端接不同负载（短路、开口、喇叭天线、匹配负载）时系统中形成的驻波分布情况◆掌握用直读法测量负载驻波比的方法测量线探针等效◆测量线调整◆探针伸入波导内◆→引入不均匀性◆→等效：◆gp反映探针吸取功率的大小◆bp反映探针在波导中产生反射的影响◆端接任意负载时→gp分流，驻波波腹点电场强度比真实值小;◆bp会使驻波波腹点和波节点位置发生变化;测量线调整原理◆终端短路→波节点处Yin →唴→波节位置不会偏移◆终端短路→波腹点处Yp 影响明显→波节位置因探针容性电纳bp的存在→驻波波腹点向负载方向偏移◆减小Yp的影响◆gp：适当减少探针插入深度;◆bp：调整探针的调谐电路；测量线调整方法◆调整方法◆探针深度：1.0~1.5mm(一般不需调整!)◆终端短路◆→探针移至波腹位置◆→调节测量线上的调谐活塞◆→选放指示最大◆测量之前,先移动测量线探针观察某个波节点到相邻波腹点之间的间隔,如果比四分之一波导波长大(或小)很多,就需要进行调谐◆注意事项◆频率改变，调谐要重新进行！驻波分布终端阻抗◆端接负载◆终端短路：测量线终端接短路板◆终端开路：测量线终端开路◆终端开口：测量线终端开口（空载）◆终端匹配：测量线终端接匹配负载◆注意事项◆终端开路与开口的区别短路活塞确定等效开路面的方法◆保证短路活塞法测量膜片电纳准确的关键是要准确调节短路活塞的位置使它离测量线终端的距离为(2n+1)λg/4(即等效开路面)，其方法是：首先移动测量线探针到dT处，保持其位置不变。

测量线终端接上可调短路器，旋动短路活塞，使测量放大器电表指示变至最大，即使得可调短路器成为开路器件。

用交叉读数法来确定等效开路面的位置。

驻波分布测量方法◆驻波分布测量方法◆测量线终端接待测负载◆→移动测量线探针◆→按一定方式记录探针位置和检波指示值（d~i）◆→描绘驻波分布特性图形驻波比测量原理◆驻波比（ρ,s)：描述驻波分布状态的重要参数◆小信号工作，平方律检波条件下，实验中可由如下公式得到驻波比◆Imax和Imin分别是驻波波腹点和波节点的检波电流值驻波比测量方法◆驻波比的测量方法-直接法◆测量线终端接上待测负载◆→移动探针至测量线中间部位的波腹点◆→调整信号大小使波腹点的检波指示值达到满量程◆→移动探针至相邻波节点◆→读取指针指示的选频放大器驻波比刻度线上的刻度值◆→得到驻波比的值◆注意事项◆直接法测驻波比，最大可测量值小于10直接法测量步骤•测量线探针放置波腹点位置时,调整指示至满量程;•移动测量线探针至相邻波节点,读取驻波比刻度线上的值,即为S;•如果超过1-4量程,则增大一档选放分贝档,读取3.2-10量程上的值;测量系统框图测量要求◆系统调整◆工作方式：方波调制◆工作频率：9370MHz◆测量内容◆按驻波分布的测量方法以及驻波比的测量方法分别测量终端短路、开路、开口、匹配四种负载的驻波分布特性及驻波比的大小；测量要求◆驻波分布测量要求:(系统状态要求)◆在短路情况下将波腹点的检波指示值通过衰减调节调至2/3量程,不要调到满量程;◆在开口以及匹配负载情况下保持系统状态不变时进行测量;◆测完驻波分布后,用直接法测量驻波比;◆测量开始位置◆从负载至信号源方向◆选择测量线一个合适位置作为测量起始位置（终端短路状态时的波节点）测量要求◆驻波分布测量要求:(测量数据量)◆短路、开路、开口：测量数据要求:◆至少包括两个波节点,三个波腹点,且相邻波节和波腹点之间测量点不得少于4个;◆匹配负载：情况下根据实际观测量适当数据点;◆驻波比测量◆按驻波分布相反的测量顺序用直接法测量驻波比◆匹配负载、开口实验数据记录实验报告处理要求◆根据测量数据，在同一坐标系下，描绘四种负载的驻波分布；◆根据测量数据，运用公式计算待测负载的驻波比，并与直接法测量的数据作比较。