- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Xi
Zi
Zj Yj
cosθ j R( Z i ,θ ) = sin θ i 0
− sin θ cosθ 0
0 0 1
Xi
θ
Xj
θ
Yi
0 1 j R( X i ,θ ) = 0 cosθ i 0 sin θ
− sin θ cosθ 0
j i
R
j
P
►姿态矢量矩阵
cos(∠X ' X ) cos(∠Y ' X ) cos(∠Z ' X ) O' R = cos(∠X ' Y ) cos(∠Y ' Y ) cos(∠Z ' Y ) O cos(∠X ' Z ) cos(∠Y ' Z ) cos(∠Z ' Z )
φ
Xi
X1 X 2 X j
2)、绕固定坐标系旋转
( X i , α) ( Z i , θ)
坐标系 ( X i , Yi , Z i )
Zi Zm Zj
坐标系( X m , Ym , Z m )
j i
坐标系 ( X j , Y j , Z j )
θ α θ α
Yj Ym Yi
R=?
证明与讨论: 证明与讨论
− cosϕ cosθ sin φ − sin ϕ cosφ − sin ϕ cosθ sin φ + cosϕ cosφ sin θ sin φ
cosϕ sin θ sin ϕ sin θ cosθ
注意:多个旋转矩阵连乘时,次序不同则含义不同。
1)绕新的动坐标轴依次转动时,每个旋转矩阵要从左往右 左往右 乘,即旋转矩阵的相乘顺序与转动次序相同; 2)绕旧的固定坐标轴依次转动时,每个旋转矩阵要从右往 右往 左乘,即旋转矩阵的相乘顺序与转动次序相反。
cosθ j R (Yi ,θ ) = 0 i − sin θ
0 sin θ 1 0 0 cosθ
cosθ j R( Z i ,θ ) = sin θ i 0
− sin θ cosθ 0
0 0 1
转动矩阵的特点: 转动矩阵的特点: (1) 主对角线上有一个元素为1,其余均为转角的余弦/正弦; (2) 绕轴转动的次序与元素1所在的行、列号对应; (3) 元素1所在的行、列,其它元素均为0; (4) 从元素1所在行起,自上而下,先出现的正弦为负,后出现 的为正,反之依然。
《机器人学》 机器人学》
第三章 机器人的位姿描述与坐标变换 战强
北京航空航天大学机器人研究所
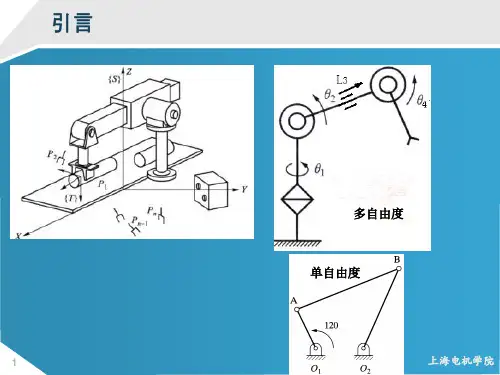
第三章 机器人的位姿描述与坐标变换
Z Y X 机器人 的位姿
Zi Xi Zw
连杆I的 位姿 Yi
Yw Xw
3-1 刚体位姿的数学描述
假设机器人的连杆和关节都是刚体 刚体¥ ¥ ¥假设机器人的连杆和关节都是刚体¥ ¥
− sin ϕ cos ϕ 0
0 cosθ 0 0 1 − sin θ
0 sin θ cos φ 1 0 sin φ 0 cosθ 0
− sin φ cos φ 0
0 0 1
cosϕ cosθ cosφ − sin ϕ sin φ = sin ϕ cosθ cosφ + cosϕ sin φ sin θ sin φ
☺
9个元素,只有3个独立, 满足6个约束条件:
O' O O' O
X .O ' X = O
O' O
Y .O ' Y O
= O 'Z .O ' Z = 1 O O
X .O ' Y = O 'Y .O ' Z = O 'Z .O ' X = 0 O O O O O
R −1 = O 'R T O R =1
☺
O' O
R是单位正交阵
O' O
刚体的位置和姿态:
{O'} ={O ' R , O
O' O
P}
Zj
例:某刚体j在参考系i中的 位置 姿态
oj oi
P=?
Oj Oi
R=?
Xj Zi
Oj
Yj
6
10
Oi
Xi
Yi
3-2 坐标变换(点的映射) 坐标变换(点的映射)
1、坐标平移(坐标系方位相同) 、坐标平移(坐标系方位相同)
x0 刚体位置: o 刚体位置: o ' P = y 0 z0
X Z b Z' O' O n X' Y' t
Y
刚体姿态: 刚体姿态:
O' O
R = [ O' X O
O' O
Y
单位主矢量
cos(∠X ' X ) cos(∠Y ' X ) cos(∠Z ' X ) O' Z ]3×3 = cos(∠X 'Y ) cos(∠Y 'Y ) cos(∠Z 'Y ) O cos(∠X ' Z ) cos(∠Y ' Z ) cos(∠Z ' Z )
− sin θ cos α cosθ cos α sin α
sin θ sin α − cosθ sin α cos α
2)、绕运动坐标系旋转
坐标系 ( X i , Yi , Z i ) 坐标系 ( X 1 , Y1 , Z 1 ) 坐标系 ( X 2 , Y2 , Z 2 ) 坐标系 ( X j , Y j , Z j )
θ α
j i
R (α ,θ ) = R( Z ,θ ) R( X , α )
Xi
Xm
θ
Xj
i
cosθ j R (α ,θ ) = sin θ 0
− sin θ cosθ 0
0 1 0 0 0 cos α 1 0 sin α
0 cosθ − sin α = sin θ cos α 0
证明: 1)绕运动坐标系旋转
R(Z i ,ϕ )
坐标系 ( X i , Yi , Z i )
Z2 Zj Z i (Z1 )
R(Y1 ,θ ) R(Z 2 , φ ) 坐标系 ( X 1 , Y1 , Z 1 ) 坐标系 ( X 2 , Y2 , Z 2 )
坐标系 ( X j , Y j , Z j )
适用的机器人类型举例(有平移关节)
Z1 X1
Y1 Z2 X2
Y2
Z3 X3
Y3
三坐标的直角坐标机器人
Z
Y
X
Zi
Zj
例: Oi
Yi Xi Xj
•P
Oj
Yj
15 已知
j
P = [− 5 6 7]
T
求 P点在i坐标系中的坐标。
T T
解答: i P = j P + OjP
i
= [− 5 21 7]
= [− 5 6 7] + [0 15 0]
j i
Yj (Y2 )
ϕ φ θ
R=?
1) P2 = 2j R ⋅ Pj = R( Z 2 , φ ) Pj
Y1 Yi
φ
ϕ
θ
2 2) P =1 R ⋅ P2 = R(Y1 ,θ ) P2 1
ϕ
θ
3) Pi =i1R ⋅ P = R( Z i , ϕ ) P 1 1 = R( Z i , ϕ ) R(Y1 ,θ ) P2 = R( Z i , ϕ ) R(Y1 ,θ ) R( Z 2 , φ ) Pj
cos(∠X i , X j ) cos(∠X i , Y j ) cos(∠X i , Z j ) x j i P = cos(∠Yi , X j ) cos(∠Yi , Y j ) cos(∠Yi , Z j ) y j cos(∠Z , X ) cos(∠Z , Y ) cos(∠Z , Z ) z i j i j i j j
Z2
ϕ φ θ
Z i (Z1 )
R(Zi ,ϕ )
j i
R(Y1 ,θ )
R(Z 2 , φ )
Zj
R(ϕ ,θ , φ ) = R ( Z , ϕ ) R (Y ,θ ) R ( Z , φ )
ZYZ欧拉角
ϕ
θ
φ
Yj (Y2 )
ϕ
θ
Y1 Yi
φ
Xi
X1 X 2 X j
cos ϕ j R(ϕ ,θ , φ ) = sin ϕ i 0
θ θ
Xi Xj Yi
3)RZ
Zi Z
j
θ θ
Yj Yi
Xi
Xj
cos(∠X i , X j ) cos(∠X i , Y j ) cos(∠X i , Z j ) x j i P = cos(∠Yi , X j ) cos(∠Yi , Y j ) cos(∠Yi , Z j ) y j cos(∠Z , X ) cos(∠Z , Y ) cos(∠Z , Z ) z i j i j i j j
T
2、坐标旋转(坐标系原点相同) 、 坐标系原点相同)
Zj Zi P
坐标系j由坐标系i旋转而成 已知点P在j坐标系的坐标:
Yj
j
P = [x j
yj
z j ]T
Yi Xi Xj
求点P在i坐标系的坐标:
i
P = [ xi
yi
zi ]T
Zj
Zi
zi


位姿描述与齐次变换PPT](https://uimg.taocdn.com/711ba841caaedd3383c4d3c4.webp)