当前位置：文档之家 › 第四讲 机器人的位姿描述

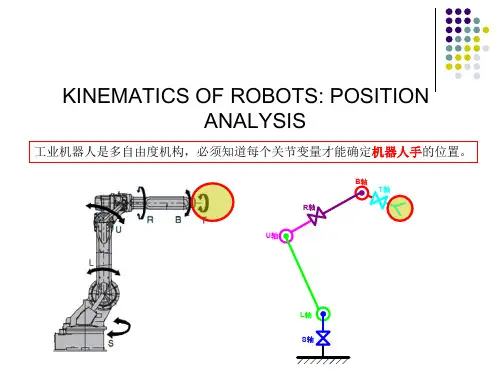
第四讲 机器人的位姿描述

  • 格式：ppt
  • 大小：782.00 KB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

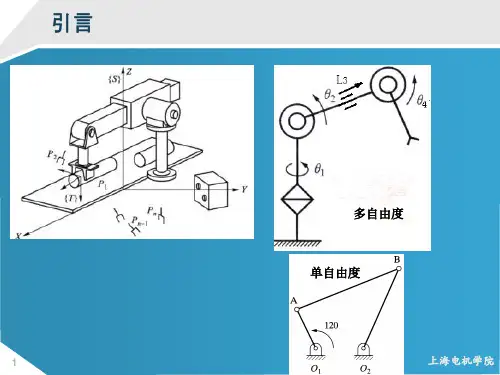
工业机器人位姿描述资料

工业机器人位姿描述资料

齐次变换法 矢量法
位姿描述
旋量法 四元数法
5
上海电机学院
位姿描述——点的位置描述
1.点的位置描述{位置矢量}
对于直角坐标系{A}，空间任一点P的位置可用3×1的列矢量 表示。
px
A
P
p
y
pz
AP的上标A代表参考坐标系｛A｝。
6
上海电机学院
位姿描述——姿态的描述(旋转矩阵)
姿态可由某个固连于此物体的坐标系描述。 BAR [AxB ,AyB, A zB ]
nx ox ax
A B
R
ny
oy
a
y
nz oz az
旋转矩阵
7
上海电机学院
位姿描述——姿态的描述(旋转矩阵)
nx ox ax cos(n, x) cos(o, x) cos(a, x)
A B
R
ny
oy
a
y
cos(n,
y)
cos(o, y)
cos(a, y)
nz oz az cos(n, z) cos(o, z) cos(a, z)
(1)点的齐次坐标
px
AP
py
pz
齐次坐标
px
p
y
pz
1
注意： 齐次坐标的表示不是惟一的。
P px py pz 1 T px py pz T a b c T
11
上海电机学院
位姿描述——齐次坐标
规定：
(1) (4×1)列阵[a b c ω]T中第四个元素不为零，则表示空间某点的 位置；
14
上海电机学院
位姿描述——动坐标系位姿的描述
静系
在机器人坐标系中，运动时相对 于连杆不动的坐标系称为静坐标

机器人的位姿描述与坐标变换

机器人的位姿描述与坐标变换

0
1
0
⎥ ⎥
⎢⎣− sinθ 0 cosθ ⎥⎦
Zi Zj
θ
θ Xi
Xj
Yi Y j
⎡cosθ − sinθ 0⎤
j i
R(Zi
,θ
)
=
⎢⎢sinθ
cosθ
0⎥⎥
⎢⎣ 0
0 1⎥⎦
Zi Zj
θ
Xi Xj
Yj
θ
Yi
⎡1 0
0⎤
j i
R(
X
i
,θ
)
=
⎢⎢0
cosθ
−
sinθ
⎥ ⎥
⎢⎣0 sinθ cosθ ⎥⎦
￥ ￥假设机器人的连杆和关节都是刚体￥ ￥
位置矢量
⎡x0 ⎤
P o '
o
=
⎢ ⎢
y0
⎥ ⎥
⎢⎣ z0 ⎥⎦
Z b Z'
O' Y' t n X' O
X Y
姿态矢量
O' O
R
=
[
O' O
X
OO'Y
⎡cos(∠X ' X )
O' O
Z
]3×3
=
⎢ ⎢
cos(∠X
'Y
)
⎢⎣cos(∠X ' Z )
单位主矢量
cos(∠Y ' X ) cos(∠Y 'Y ) cos(∠Z ' Z )
cos(∠Z ' X )⎤
cos(∠Z
'Y
)
⎥ ⎥
cos(∠Z ' Z ) ⎥⎦
姿态矩阵R的特点：

机器人学技术基础课程-位姿描述和齐次变换

机器人学技术基础课程-位姿描述和齐次变换
2、齐次变换在研究空间机构动力学、机器人控制算法、计算 机视觉等方面也得到广泛应用。
位姿描述与齐次变换
1 刚体位姿的描述 2 坐标变换 3 齐次坐标系和齐次变换 4 齐次变换矩阵的运算 5 变换方程
2.1 刚体位姿的描述
为了完全描述一个刚体在空间的位姿，通常将刚体与某 一坐标系固连，坐标系的原点一般选在刚体的特征点上，如 质心、对称中心等。
YˆB ZˆA
ZˆB Xˆ A ZˆB YˆA

ZˆB ZˆA

XB n
2.1.4 旋转矩阵的意义
若坐标系B可由坐标系A,通过绕A的某一坐标轴获得,则绕 x,y,z三轴的旋转矩阵分别为：
1 0 0
c 0 s
c s 0
R(x, ) 0
Ay
y
所以： A Axaˆx Ayaˆy Azaˆz
2.1.2 方位的描述
矢量： A Axaˆx Ayaˆy Azaˆz
模的计算： | A | Ax2 Ay2 Az2
z
Az
A

方向角与方向余弦：, ,
o

Ay
Ax

y
x
cos Ax = A aˆx , cos Ay = A aˆy , cos Az A aˆz
两矢量的叉积又可表示为：
aˆx aˆy aˆz A B Ax Ay Az
Bx By Bz
2.1.2 方位的描述
空间物体B的方位(Orientation)可由某个固接于此物体的坐标系{B}的三 个单位主矢量[xB,yB,zB]相对于参考坐标系A的方向余弦组成的3x3矩阵描述.
BAR n o a a

机器人技术基础实验报告2(机器人空间位姿描述)

机器人技术基础实验报告2(机器人空间位姿描述)

机器人技术基础实验报告班级：学号：姓名：台号： 2 课程：2.机器人空间位姿描述成绩：批改日期：教师签字：实验目的：1、认识机器人位置与姿态的描述方式2、了解多种姿态的描述方法实验设备及软件:1、珞石XB4机器人2、MATLAB实验原理:位置描述：建立坐标系后可以用一个3×1的位置矢量对坐标系中的任何点进行定位。

用三个相互正交的带有箭头的单位矢量来表示一个坐标系{A}.用一个矢量来表示一个点P A ，并且可等价地被认为是空间的一个位置矢量，或者简单地用一组有序的三个数字来表示。

矢量的各个元素用下标x，y和z 来标明：姿态描述：为了描述物体的姿态，需要在物体上固定一个坐标系并且给出此坐标系相对于参考系的表达。

用X B 、Y B和Z B来表示坐标系{B}主轴方向的单位矢量。

在用坐标系{A}的坐标表达时，写成X B A、Y B A、Z B A。

这三个单位矢量按照顺序排列组成一个3×3的矩阵，称之为旋转矩阵。

记为：R B A= [X B A Y B A Z B A]分别绕X 轴，Y轴，Z轴的旋转变换为：坐标系变换是一个坐标系描述到另一个坐标系描述的变换。

被描述的空间点本身没有改变，只是它的描述改变了。

一般情况下坐标系{A}与坐标系{B}既存在位置差异又存在姿态差异。

则相对于坐标系{B}描述的点PB在坐标系{A}下的描述为：AP A=R B A P B+P BORG为了简化表达，可改写为：[P A1]=[R B A P BORG A 01][P B 1]=T B A[P B 1] 其中T B A =[RB A P BORGA01]为4×4矩阵，称为齐次变换矩阵。

描述了坐标系{B} 相对于坐标系{A}的变换。

姿态其他描述： X-Y-Z 固定角 等效转轴表示法 X-Y-Z 欧拉角 四元素法 1、X-Y-Z 固定角:坐标系{B}的方位规则如下：最初坐标系{B}与{A}重合，转动相对固定坐标系{A}来描述，先绕X A 轴转γ 角 ，再绕Y A 轴转β角，最后绕Z A 轴转α角。

机器人的位姿描述与坐标变换

机器人的位姿描述与坐标变换

j i
R (a , ) R( Z , ) R( X , a )
Xi
Xm

Xj
cos sin j i R (a , ) 0
sin cos 0
0 1 0 0 cos a 0 1 0 sin a
0 cos sin sin a cos a 0
Yj
xi
Xi
yi
Yi
xj
Xj
xi x j cos(X i , X j ) y j cos(X i , Y j ) z j cos(X i , Z j ) i P yi x j cos(Yi , X j ) y j cos(Yi , Y j ) z j cos(Yi , Z j ) z x cos(Z , X ) y cos(Z , Y ) z cos(Z , Z ) j i j j i j j i j i
T
5 21 7
2、坐标旋转（坐标系原点相同）
Zj Zi P
坐标系j由坐标系i旋转而成 已知点P在j坐标系的坐标：
Yj
j
P [x j
yj
z j ]T
Yi Xi Xj
求点P在i坐标系的坐标：
i
P [ xi
yi
zi ]T
Zj
Zi
zi
P
yj
zj
Yj
xi
Xi
yi
Yi
xj
Xj
☺ 关于(Yi , X j )？
Z2 Z i (Z1 )
j f
R(Z i ,j )
j i
R(Y1 , )
R(Z 2 , f )
Zj

[课件](工业机器人)位姿描述与齐次变换PPT

[课件](工业机器人)位姿描述与齐次变换PPT
六、齐次表达
根据几何学知识，上面第四小节中给定点的绝对位置为：
Ap b a b a b a c s cs b a
写成三维形式，有：
a a a c s 0a Apbbbs c 0b
3. 试按照运动顺序计算相关基本变换矩阵相乘结果
c s 0 a
Tra(An a,A sb,A0)Ro(zA t,)s0
c
0
0 b 1 0
0
1
4. 计算结果比较
两种方法结果相同！但后一种方法简单！
问题：是否仅仅按照运动变换顺序将相关的基本变 换矩阵相乘，即可以得到齐次变换阵？
0 0 0 0 0 10
O B 在A中位置，记作 A pOB
B在
A 中姿态，记作
A B
R
。
分成两块，不便于记忆！
齐次变换矩阵
若写成如下齐次形式，有：
c s 0 aa
A 1ps0 0
c
0 0
0 1 0
A 中的位置，然后与
b
A坐标原点值相加即可
得到该点绝对位置。
OA
由几何法，得：
aacbs 写成矩阵形式
b as bc

Y A
YB
b
b
XB a

OB
a
X A
a
XA
相
a c sa 对
bs cb
坐 标 值
b 1 0b 1 0B A 0R
Ap 1OBB 1pA BTB 1p
七、齐次变换矩阵
1. 构成：分为4块。左上角是姿态矩阵，为一单位正交 矩阵；右上角为对象坐标系原点位置值；左下角为 三个0 0 0，简记为0；右下角为1。

机器人的位姿描述课件

意义
通过位姿描述，可以确定机器人 在空间中的位置、朝向和姿态， 对于机器人运动学、导航、遥控 等领域具有重要意义。
机器人位姿的表示方法
欧拉角表示法
以绕三个轴（横滚、俯仰、偏 航）的旋转角度为基础，描述
机器人的姿态和朝向。
方向余弦矩阵表示法
通过三个方向的单位向量和三 个方向的旋转角度，构建一个 方向余弦矩阵，描述机器人的 姿态和朝向。
总结词
精准、稳定、高效
详细描述
工业机器人通常需要高精度、稳定性和效率来提高生产效率、产品质量和降低生产成本。位姿控制策 略是实现这些目标的关键技术。通过对工业机器人的运动学和动力学模型进行分析和优化，可以实现 对机器人位姿的高精度控制。
全
详细描述
手术导航
医疗机器人在手术导航中通过位姿描述， 实现精确的手术定位和操作。
康复治疗
医疗机器人在康复治疗中，通过位姿描述 评估患者的运动功能和康复进展。
辅助行走
医疗机器人在辅助行走中，通过位姿描述 实现稳定、安全的行走辅助。
航空航天机器人
空间探索
航空航天机器人在空间探索中通过位姿描 述，实现精确的物体抓取和运输。
无人机配送
航空航天机器人在无人机配送中，通过位 姿描述实现准确、高效的配送服务。
机场跑道清扫
航空航天机器人在机场跑道清扫中，通过 位姿描述实现高效、安全的清扫作业。
04
机器人位姿描述的挑战与解决方案
传感器误差与位姿估计
传感器误差
机器人的传感器在获取自身及环境信息时存在误差，包括安装偏差、测量不准确 等问题，对位姿估计造成影响。
平移向量
平移向量是用于描述物体在空间中沿 某三个方向移动的向量，通常用三个 连续的数值表示。通过平移向量，可 以确定机器人在空间中的位置。

机器人的位姿运动学

z
PAB (Bx Ax )i ( By Ay ) j ( Bz Az )k
ax P b y cz
x
P
cz by ax
y
【空间向量的表示】
Application of a scale factor


Makes the matrix 4 by 1 Allows for introducing directional vectors
S 1 0 0 C 0
Representation of Combined Transformations
【复合变换的表示】

1. 2.
Example:
Rotation of degrees about the x-axis, Followed by a translation of [l1,l2,l3] (relative to the x-, y-, and z-axes respectively), Followed by a rotation of degrees about the y-axis.
nx n F y nz 0
ox oy oz 0
ax ay az 0
px py pz 1
【齐次变换矩阵】
3. 变换的表示 Representation of Transformations
当空间的坐标系（向量、物体或运动坐标系）相对于固定的参考坐 标系运动时，这一运动可以用类似于表示坐标系的方式来表示。
z
Axis
px pn p y l1 l2 po cos pa sin pz l3 l4 po sin pa cos

机器人运动学第四讲


3.1 机器人的位姿描述 一、机器人位姿的表示 1、位置的表示 坐标系建立后，任意点p在空间的位 置可以用一个3×1的位置矢量来描述； 例如，点p在{A}坐标系中表示为：
ｚ ｐ(ｘ,ｙ,ｚ)
px A P py pz
ｘ
ｏ
{A}
ｙ
山东大学机械工程学院机电工程研究所2010/09/02
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
4、常用的旋转变换 ①、绕z轴旋转θ 角 坐标系{i}和坐标系{j}的原点合， 坐标系{j}的坐标轴方向相对于坐标系{i} 绕轴旋转了一个θ 角。θ 角的正负一般 按右手法则确定，即由z轴的矢端看，逆 ｚi 时钟为正。 ｚ
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
• 若给定一旋转矩阵:
r11 R K ( ) r21 r31 r12 r22 r32 r13 r23 r22
• 则可计算出：
山东大学机械工程学院机电工程研究所2010/09/02
α
ｙi
ｘi
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
③绕y轴旋转β角的旋转变换矩阵为：
ｚi ｚj
β
ｏi
ｏj
β
ｙj ｙi
ｘi
ｘj
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
• 绕任意轴的转动 设绕k轴转动θ 角，则旋转矩阵为：
其中：
0 0 1 0
px x j py y j pz z j 1 1

04-机器人课程-运动学


1、机器人运动学
1.5机器人微分运动及速度
机器人的微分运动是研究机器人关节变量的微小变化与机器人手部位姿的微小变化 之间的微分关系。如果已知两者之间的微分关系，就可以解决机器人微分运动的两 类基本问题：一类是在已知机器人各个关节变量的微小变化时求机器人手部位姿的 微小变化；另一类是在已知机器人手部位姿的微小变化时求机器人各个关节变量相 应的微小变化。机器人的微分运动对机器人控制、误差分析、动力分析和保证工作 精度具有十分重要的意义。
1、机器人运动学
1.3齐次变换及运算
1.3.1 直角坐标变换 在机器人中建立直角坐标系后，机器人的手部和各活动杆件之间相对位 置和姿态就可以看成是直角坐标系之间的坐标变换。
1、机器人运动学
1.3齐次变换及运算
平移变换 设坐标系{i}和坐标系{j}具有相同的姿态，但两者的坐标原点不重合，如图3-7所 示。 若用矢量Pij表示坐标系{i}和坐标系{j}原点之间的矢量，则坐标系{j}就可以看成 是由坐标系{i}沿矢量Pij平移变换而来的，所以称矢量Pij为平移变换矩阵，它是一个 3×1的矩阵
1.1、机器人位姿描述
机器人的位姿主要是指机器人手部在空间的位置和姿态，有 时也会用到其他各个活动杆件在空间的位置和姿态。需要先 了解的与机器人运动相关的一些基础知识。 机器人的机构运动简图、机器人的自由度、机器人的坐标系、 机器人的工作空间、机器人的位姿
1、机器人运动学
1.2机器人的位姿
所谓机器人的位姿主要就是指机器人手部在空间的位置和姿态。有了机器 人坐标系，机器人手部和各个活动杆件相对于其他坐标系的位置和姿态就 可以用一个3×1的位置矩阵和一个3×3的姿态矩阵来描述。如图3-2所示， 机器人手部的坐标系{H}相对于机座坐标系{O}位置就可以用坐标系{H}的 原点OH在坐标系{O}三个坐标分量xOH、yOH、zOH、组成3×1的位置矩阵来 表示
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3.1 机器人的位姿描述
2、姿态（或称方向）的表示 我们知道：两个刚体的相对姿态可 以用附着与它们上的坐标系的相对姿态 来描述。
山东大学机械工程学院机电工程研究所2010/09/02
3.1 机器人的位姿描述
刚体的姿态可以用附着于刚体上的坐标 系（用{B}表示）来表示；因此，刚体相对 于坐标系{A}的姿态等价于{B}相对于{A}的 姿态。 坐标系{B}相对于{A}的姿态表示可以用 坐标系{B}的三个基矢量xB、yB和zB在{A}中 的表示给出， 即[AxB AxB AxB] （这里前上标A 说明：{B}的三个基矢量在A坐标系中表示） ，它是一个3×3矩阵，它的每一列为 {B}的 基矢量在{A}中的分量表示。
意义：左上角的3×3矩阵是两个坐标系之 间的旋转变换矩阵，它描述了姿态关系； 右上角的3×1矩阵是两个坐标系之间的平 移变换矩阵，它描述了位置关系，所以齐 次坐标变换矩阵又称为位姿矩阵。
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
联合变换与单步齐次变换矩阵的关系： 任何一个齐次坐标变换矩阵均可分解 为一个平移变换矩阵与一个旋转变换矩阵 的乘积，即：
cos sin RZ ( ) 0
sin cos 0
0 0 1
2013年12月1日星期日
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
②、绕x轴旋转α角的旋转变换矩阵为：
ｚi
ｚj
α
ｙj ｏi ｏj ｘj
α
ｙi
ｘi
x y z x ,y ,z k k k
( x, y, z, k ) 是空间该点的齐次坐标。
则称
以后用到齐次坐标时，一律默认k=1 。
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
2、齐次坐标变换 为何使用齐次坐标？ 在进行联合变换时，变换关系为：
i
•
A B
A B
R R R
A B T B A
山东大学机械工程学院机电工程研究所2010/09/02
1
3.1 机器人的位姿描述
3、位姿的统一表示 定义一组四向量矩阵[R P]，如图。其中， i i p jorg 表示{j}相对{i}的姿态， 表示{j}的原点 jR 相对{i}的位移。 我们可以将{j}坐标 ｚj 系相对{i}坐标系描述为： ｚi
山东大学机械工程学院机电工程研究所2010/09/02
3.1 机器人的位姿描述 即：
A B
R A xB

A
yB
xB x A x y A zB B A xB z A

yB x A yB y A yB z A
T zB xA B X A BY T zB y A A T zB z A B Z A


12 0.866 0.5 0 5 11.830 rA p AB RAB rB 6 0.5 0.866 0 9 13.794 0 0 0 1 0 0
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
解：由题意可得平移变换矩阵和旋转变换 矩阵分别为：
p AB 12 6 0
和
则：
cos30 sin 30 0 0.866 0.5 0 RAB z (30 ) sin 30 cos30 0 0.5 0.866 0 0 0 1 0 0 1
基矢量都是单位矢量，因此，上式又 可以写成：
A B
cos( xA x B ) cos( xA y B ) cos( x Az B ) , , , R cos( yA x B ) cos( y A, y ) cos( y Az B ) , , B cos( zA x B ) cos( zA yB ) cos( zA z B ) , , ,
px p A P y pz
其中px，py，pz为P点的 坐标分量。
ｘ
ｚ
ｐ(ｘ,ｙ,ｚ)
ｏ
{A}
ｙ
山东大学机械工程学院机电工程研究所2010/09/02
• 位置矢量不同于一般矢量，它的大小与坐 标原点的选择有关。
山东大学机械工程学院机电工程研究所2010/09/02
• 绕任意轴的转动 设绕k轴转动θ 角，则旋转矩阵为：
其中：
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
• 若给定一旋转矩阵:
r11 R K ( ) r21 r31 r12 r22 r32 r13 r23 r22
• 则可计算出：
i i
py j yi j p pz j z i j p
i
ｚi ｚj
p
即：
p R p
i j j
ｏi ｘi ｏj ｘj
ｙj
ｙi
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
3、另一种解释 对同一个数学表达式可以给出多种不 同的解释，前面介绍的是同一个向量在不 同的坐标系的表示之间的关系。 上述数学关系也可以在同一个坐标系 中解释为向量的“向前”移动或旋转，或 则，坐标系“向后”的移动或旋转。
j
ｏi ｘi ｏj
θ
θ
ｙj
ｙi
山东大学机械工程学院机电工程研究所2010/09/02
ｘj
3.2 齐次变换及运算
xi cos y sin i zi 0 令:
sin cos 0
0 x j y 0 j 1 z j
p ji R j p i p jorg
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算 将其写成统一的矩阵形式则有：
x i cos y sin i zi 0 1 0 sin cos 0 0 0 0 1 0 px x j py y j pz z j 1 1
第3章 机器人运动学
3.1 机器人的位姿描述
3.2 齐次变换及运算
3.3 机器人运动学方程
3.4 机器人微分运动
山东大学机械工程学院机电工程研究所2010/09/02
机器人的任务
山东大学机械工程学院机电工程研究所2010/09/02
第3章
机器人运动学
运动学研究的问题： 手在空间的位姿 及运动与各个关节的 位姿及运动之间的关 系。 其中： 正问题：已知关节运 动，求手的运动。 逆问题：已知手的运 动，求关节运动。
nx n M ij y nz 0 ox oy oz 0 ax ay az 0 p x 1 p y 0 p z 0 1 0 0 0 1 0 0 1 0 0 p x nx p y n y p z nz 1 0 ox oy oz 0 ax ay az 0 0 0 0 1
山东大学机械工程学院机电工程研究所2010/09/02
3.1 机器人的位姿描述
R 称为坐标系{B}相对{A}的旋转矩阵。 旋转矩阵的性质： 1、列向量两两正交，行向量两两正交。 2、列向量和行向量都是单位向量。 3、每一列是{B}的基矢量在{A}中的分量表示，同 样，每一行是{A}的基矢量在{B}中的分量表示。 4、旋转矩阵是正交矩阵，其行列式等于1。 5、它的逆矩阵等于它的转置矩阵，即：
i' i
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
若坐标系{i}和坐标系{j}之间是先旋 转变换，后平移变换，则上述关系是应 如何变化？
i
p R（ p p jorg）
i j j i
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算 例：已知坐标系{B}沿坐标系{A}的x轴移动 12个单位，并沿坐标系{A}的y轴移动6个单 位，绕坐标系{A}的z轴旋转30°，求平移 变换矩阵和旋转变换矩阵。 假设某点在坐标系{B}中的矢量 为 rB 5i 9 j 0k ，求该点在坐标系{A}中 的表示。
i
P j P i Pjorg
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算 2、旋转 设坐标系{i}和坐标系{j}的原点重 合，但它俩的姿态不同。设有一向量P， 它在{j}坐标系中的表示为jP，它在{i} 中如何表示？ 考虑分量：
i
p x i x j p j x i j p
山东大学机械工程学院机电工程研究所2010/09/02
3.2 齐次变换及运算
4、常用的旋转变换 ①、绕z轴旋转θ 角 坐标系{i}和坐标系{j}的原点合， 坐标系{j}的坐标轴方向相对于坐标系{i} 绕的z轴旋转一个θ 角。θ 角的正负一般 按右手法则确定，即由z轴的矢端看，逆 ｚi 时钟为正。 ｚ
山东大学机械工程学院机电工程研究所2010/09/02
3.1 机器人的位姿描述
对于机器人来说，我们最关心它的末 端执行器相对于基座的位置和姿态，简称 为位姿。 问：我们如何用一组关节参数来描述 机器人的末端执行器相对于基座的位姿？
山东大学机械工程学院机电工程研究所2010/09/02
3.1 机器人的位姿描述 一、机器人位姿的表示 1、位置的表示 坐标系建立后，任意点p在空间的位 置可以用一个3×1的位置矢量来描述； 例如，点p在{A}坐标系中表示为：
{j} { R p jorg } 3×4