探究同底指数函数与对数函数交点个数

同底指数函数与对数函数交点个数探求王乐 （吉林省长春市第二实验中学）问题如题，即xa =y 与x y a log =（10≠>a a 且，0>x ）交点个数问题。

很多教师想当然的认为答案是1个或2个，很多资料上也没给出正确答案。

有一些资料上通过几何画板等现代信息技术给出结论但没有涉及道理何在[1]。

我试图通过本文的探究给大家一个有关同底指数函数与对数函数交点个数粗略的印象，并欢迎大家讨论、指正。

我们都知道指数函数与对数函数图像的变化规律，我总结为指数函数“大大近y 轴，小小近y 轴”。

也就是底数大于1时底越大图像越靠近y 轴，底数小于1时底越小越靠近y 轴。

对数函数同理“大大近x 轴，小小近x 轴”。

有了这种变化规律的感受后，我们就可以把探究一对互为反函数x a =y 与x y a log =（10≠>a a 且，0>x ）交点个数问题转化为集中考虑两个函数相切的探究，即考虑临界问题。

由于x a =y 与x y a log =互为反函数，关于x y =对称。

所以可以论证若两个函数相切则切点一定在x y =上，且必定存在公切线。

不妨设切点为),00y x （，其中00y x =。

x a y = ，a a y x ln ='，a a y x x x ln |00='=x y a log =，ax y ln 1='，a x y x x ln 1|00='= ax a a x ln 1ln 00=∴① 又因为切点),00y x （在曲线上，所以有 000x a y x ==② 000log x x y a ==③将②代入①得ax 220ln 1= ，即a x ln 10=或a x ln 10-= 由③得a x x ln ln 00=进而得出1ln 0=x 或1ln 0-=x 。

即e x =0或e x 10=代入②得e e a 1=或e e a -=此时切点分别为),(e e 或),(11--e e对应两条切线分别为x y =与12-+-=e x y ，如图（1）、（2）所示。

∙同底的指数函数与对数函数的交点问题∙需要具备的知识点指数函数一般地，形如y=a^x(a>0且a≠1) (x∈R)的函数叫做指数函数(exponential function) ，。

单调性：单调递减（0<a<1）,单调递增(a>1);对数函数单调性：单调递减（0<a<1）,单调递增(a>1);以上指数函数和对数函数的底数都用a表示。

求同底指数函数对数函数的交点方法：假设+渐近简要分析：首先看a>1还是0<a<1,高中范围内一般只考虑这两种情况.a>1交点数可能有三种情况，0个1个或2个.如下图0<a<1时图象有且仅有一个交点，我稍作说明。

Q:存在函数y=a^x与y=logax（a>1,a≠1）在x属于（0,+∞）,求其交点个数。

（a^x意思是a的x次方，logax指以a为底x 的对数）A:假设一个x，使得y=a^x与y=logax为可比较的数，可以设为a的平方或立方，（因为logaa^n=n，而a^n也是一个可以求的实数，所以可以进行比较。

如a=2，则可设x=1/2，2，4，8...）用所得的指数函数值减去对数函数值。

设指数函数值减去对数函数值为delta y，如果delta y等于或小于零时，函数有交点，如果delta y大于零则函数在x处无交点。

如何验证只有一个交点？首先找到一个x使得delta y为零，然后取x左右的横坐标值x1，x2，如果x1，x2使delta y都大于零，那么可以说指数函数与对数函数有且仅有一个交点。

（如果x1，x2对应的delta y一正一负，则函数图像有两个交点。

）如何验证有二个交点？（已证）如何计算两个交点的交点坐标？（如果出题的老师没有恶意的话，是可以用这种方法算出来的）首先找到一个横坐标值x使得delta y小于零，然后在x左侧或右侧找到一个x1使得delta y大于零，则交点横坐标点在（x，x1）或（x1，x）之间，可以继续假设，知道找到使delta y等于零的x值。

高中数学论文图形计算器应用能力测试活动学生
指数函数与对数
函数交点个数的研究【研究目的】
通过图形计算器精准的图形和函数描画功能，利用代入各种不同的数据描画图像，研究对数函数和指数函数这一对反函数的交点个数。

在研究过程中，增强自己对函数的认识和理解，加深个人对数学的热爱，解决疑难问题。

【研究过程】
1.上网搜索有关资料，发现有部分老师和同学研究函数
x a y 与x y a log 的交点个数时出现了少许错误。

2.代入不同的a 值（10a a 且），用图形计算器描画函数x a y 与x y a log 的图像，发现新的现象。

3.
通过计算和不断尝试解释各种情况。

4.整理信息，得出结论。

具体实施步骤如下：
第一步：进入图形功能
1.按O 打开图形计算器。

看到如下画面：
2.通过按导航方向键，选择图形功能，按l 进入，得到画面如下：
、
第二步：输入函数，进行初步探究
1．众所周知，函数x a y 与x y a log 是以1a 为分界线，那就以
01a 和1a 先进行研究
先以5.0a 画出两个函数的图像，再加入一条函数x Y 3为参照：输入x
Y x Y Y x 35.021,log ,5.0$0.5^fl
$iwr0.5$fl
$fl
然后画出图像，可见得有一个交点：
2.再代入2.1a ，画图，出现两个交点:。

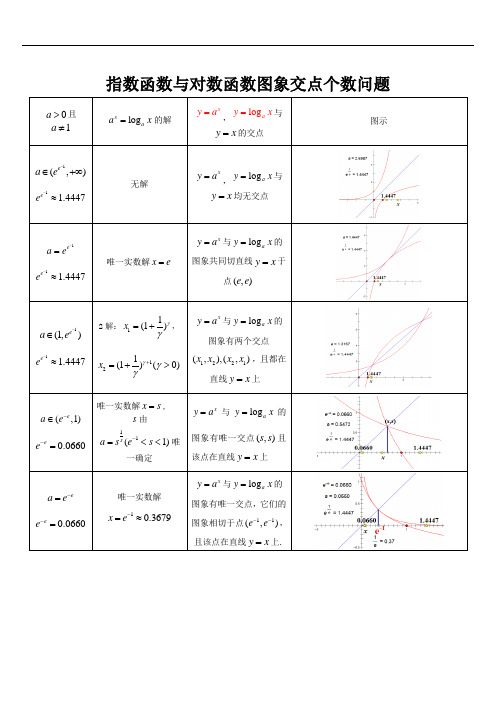
同底的指数函数与对数函数的交点问题问题：()log ,0,1xa y x y aa a ==>≠的图像在0x >上的交点个数。

解答：1.当1a >时，由二者图像的对称性知，二者图像的交点都在直线y x =上，故原问题等价于讨论()1xy aa =>与y x =在0x >上的交点的个数，等价于讨论()ln 1y x a a =>与ln y x =在0x >上的交点的个数。

令()ln ln f x x a x =-，则()1ln ,0f x a x x '=->。

当10ln x a <<时，()0f x '<，()f x 在10,ln a ⎛⎤ ⎥⎝⎦严格递减；当1ln x a >时，()0f x '>，()f x 在1,ln a ⎡⎫+∞⎪⎢⎣⎭严格递增；因此()f x 在01ln x a =处取得最小值()01lnln f x a =+。

图1 1ea e >图2 1ea e =图3 11ea e <<当()01lnln 0f x a =+>，即当1e a e >时，()0f x >在0x >上恒成立，()f x 在0x >上没有零点（如图1）；当1e a e =时，()0f x ≥在0x >上恒成立，且()010ln f x x x e a=⇔===，此时()f x 在0x >上有且仅有一个零点0x e =（如图2）；当11ea e <<时，最小值()00f x <，又因为()0111ln 1ln e x a a a<<=<-，且 ()()()()111ln 0,ln 1ln ln 01ln 1f a f a a a a a ⎛⎫=>=+-+> ⎪ ⎪--⎝⎭后式求导讨论即可验证（如下图），故()f x 在()01,x 和()01,1ln x a a ⎛⎫ ⎪ ⎪-⎝⎭上各有一个零点，又由()f x 在0x 两侧的严格单调性知这两个零点都是唯一的，故()f x 在0x >上有且仅有两个零点。

指数函数与对数函数图象交点个数问题春到四月，如火如荼，若诗似画，美到了极致，美到了令人心醉。

“你是一树一树的花开，是燕，在梁间呢喃，你是爱，是暖，是希望，你是人间的四月天”。

喜欢才女林徽因歌颂四月之美的这首《你是人间的四月天》，她将四月的万种风情描摹得淋漓尽致，读来如沐春风如饮甘露。

四月之美，美在清明。

时光刚刚跨入四月的门槛，清明就如期而至，“清明时节雨纷纷，路上行人欲断魂。

”清明是一种传承了数千年的古老文化，是一场活着的人祭奠逝去的祖先的亲情style。

“风吹旷野纸钱飞，古墓垒垒春草绿”，每到清明，人们不会忘记在天堂的祖先，都会放下手中繁忙的工作，即便远离故土，也会怀揣湿漉漉的心事回到乡下，挑拣一个最宜祭祀的日子，赶往祖先墓地，虔诚地献上一捧鲜花，点上几支香火，烧上一些纸钱，将祖先的坟墓装扮一新，以表达对已逝亲人的思念和祝福。

清明时节，最容易勾起与已逝亲人一起度过的那些美好岁月的回忆，让人深刻体悟到亲情的可贵。

于是，亲情跨越了时空，泪水模糊了双眼。

在莹莹泪光中，就让活着的人好好活着，让已经逝去的人在天堂感到欣慰。

四月之美，美在祭祖的哀思，美在人间传递着的温情。

四月之美，美在谷雨。

“清明早、立夏迟，谷雨种棉正当时”，清明过后，雨水增多，有利于谷类作物的生长。

因此，谷雨是春播春种的关键时期。

在乡间，一到谷雨时节，村民们便忙了起来，房前屋后，田间地头，处处是村民们忙碌的身影，处处嘹亮起劳动的号角，处处律动着劳作的喜悦。

他们将生活的希望播撒，将幸福的种子栽种，早出晚归，乐而不疲，笑容满面。

他们洒下的是一粒粒咸涩的汗水，成就的将是整个秋天旷野上丰硕的果实。

累了，他们举头仰望绽开在湛蓝天空上多情的太阳；倦了，他们想一想等待在前方的耀眼金秋。

春风，贴着他们的身影吹过，将灼热的期盼和梦想带向遥远、遥远……他们劳动的姿势，仿佛在大地上书写一首生活的真爱长歌；他们奔忙的步伐，舞动出四月美妙和谐的韵律；他们洋溢在嘴角的笑意，仿佛闪烁在阳光下的一朵朵桃花。

探究同底指数函数与对数函数交点个数每次教高一，我都将“同底的指数函数与对数函数的交点个数问题”作为学生的一个自主探究材料，并在课堂教学中让学生通过即兴说题，激发学生的理性思维。

本文摘录一次对这一课题的探究过程，供中学同仁教学参考。

一、提出课题在指数函数和对数函数的基础上学完反函数后，我特意安排了一节复习课，目的是加深学生对指数函数和对数函数的相关性质的认识，同时也向学生展示一个完整的数学探究案例。

一上课，我就特意营造气氛引导学生提出探究课题，先提问学生所学过的有哪些反函数，然后要求学生画出其图像。

不一会，台下叽叽喳喳起来，已有学生按捺不住向我举手提问，好戏开场了。

生A：老师！我们知道，互为反函数的两个函数其图像关于直线y=x对称，那教材上和您为什么都不把它们的图像画在同一坐标系中以更好地研究其相关性质呢？师：这个问题你提得很好，其他同学也应有类似疑问。

（教师板书：为什么不将指数函数y= 与对数函数y= (a>0，且a≠1)的图像画在同一坐标系中？？？）众生：是啊！为什么呢？师：这个问题的内涵很丰富，探究价值也很高，很值得我们一起来思考。

同学们！你们能告诉生A为什么吗？生B：可能是因为这两个函数图像的交点个数不定。

师：大家说是吗？生C：（微笑）应该是这个原因。

因为底数a是一个参数，同底的指数函数与对数函数两图像的交点个数应与底数值有关。

师：英雄所见略同，我也持与你们相同的看法。

那大家能不能就生A的问题及其他同学的分析提出一个探究课题？生D：同底的指数函数与对数函数两图像的交点个数与底数值的关系。

生E：生D的提法太抽象，目标也不明确。

我的题目是：求指数函数y= 与对数函数y= 的图像的交点个数。

掌声猛然响起。

师：改得非常好，一个“求”字就让课题生动起来了。

这节课我们就来弄清楚这两个函数图像的交点个数。

（老师板书探究课题：求指数函数y= 与对数函数y= 的图像的交点个数。

）二、数学探究师：这节课我们的探究课题是：求指数函数y= 与对数函数y= 的图像的交点个数。

同底的指数函数与对数函数的图象有几个交点作者：张松年来源：《新课程·中学》2012年第08期函数y=ax与y=logax（a>0，a≠1）的图象有几个交点？自《普通高中课程标准实验教科书·苏教版·数学必修1》提出这个问题以后，引起了中学数学教师的广泛关注。

2006年第2版《苏教版·数学必修1》第80页的例5和探究的内容是：例5：分别就a=2，a=■和a=■画出函数y=ax与y=logax的图象，并求方程ax=logax解的个数。

探究：当0教材提示利用Excel、图形计算器或其他画图软件（教学过程中一般用几何画板），在同一坐标系中分别就a=2，a=■和a=■时画出函数y=ax与y=logax的图象，通过观察，发现：在这三种情况下，两个函数图象的交点个数分别为0，2，1，从而方程ax=logax解的个数分别为0，2，1。

作为探究，用几何画板演示，可以发现：当0但问题是：这两个函数的图象到底有几个交点？会不会有4个公共点？交点个数变化时，底数a的临界值是什么？怎样找底数a的临界值呢？一、几个基本结论1.y=ax与y=logax互为反函数，它们的图象关于直线y=x对称。

如果函数y=logax的图象与直线y=x相交，那么交点必定在函数y=ax的图象上。

同样，如果函数y=ax的图象与直线y=x相交，那么交点必定在函数y=logax的图象上。

2.函数y=ax是凹函数，它的图象在其任意一条切线的上方。

证明如下：由y=ax，得y′=axlna，y″=ax（lna）2。

因为对任意的x∈R，都有ax>0，且（lna）2>0，所以y″>0，所以，函数y=ax是凹函数。

3.（1）当a>1时，函数y=logax是凸函数，它的图象在其任意一条切线的下方；（2）当0证明如下：由y=logax，得y′=■（x>0），y″=—■（x>0）。

因为对任意的x∈（0，+∞），都有x2>0，所以当a>1时，有lna>0，所以y″0，所以，函数y=logax是凹函数。

同底的指数函数与对数函数的交点问题引文：讨论底a>1与0<a<1两种情况下函数的交点个数问题。

一、实例分析（一）判断函数y=3x与函数y=log3x的交点个数对于函数y=3x,其定义域为全体实数，值域为(0,+∞)。

由于底数a=3,a>1,所以函数在定义域区间上为单调增函数。

对于函数y=log3x,其定义域为(0,+∞)，值域为全体实数。

由于底数a=3,a>1,所以函数在定义域区间上为单调增函数。

二者在同一坐标系的图像如下图：由于函数y=log3x和函数y=3x互为反函数，即关于直线y=x 对称。

从图像容易知道y=3x和y=x没有交点，所以根据对称性质，y=log3x与对称轴y=x也没有交点，即此时函数y=3x与函数y=log3x的交点个数为0.此时留下思考问题：在a>1的情况下，y=a x和y=x之间是永远相离，还是可以相切，或是相交？（二）判断函数y=（1/3）x与函数y=log1/3x的交点个数对于函数y=(1/3)x,其定义域为全体实数，值域为(0,+∞)。

由于底数a=1/3,0<a<1,所以函数在定义域区间上为单调减函数。

对于函数y=log1/3x,其定义域为(0,+∞)，值域为全体实数。

由于底数a=1/3,0<a<1,所以函数在定义域区间上为单调减函数。

二者在同一坐标系的图像如下图：由于函数y=log1/3x和函数y=(1/3)x互为反函数，即关于直线y=x对称。

从图像容易知道y=(1/3)x和y=x有一个交点，所以根据对称性质，y=log1/3x与对称轴y=x同时交于此交点，即此时函数y=(1/3)x与函数y=log1/3x的交点个数为1.此时留下思考问题：（1）在0<a<1的情况下，y=a x和y=log a x在x趋近无穷远处或者在y趋近无穷远处，会不会相交？如果有，那就是3个交点。

（2）在0<a<1的情况下，本例出现的交点是1个，但不是切点，是否还存在只有1个交点且是切点的情况？二、结论归纳（一）函数y=a x与函数y=log a x(a>1)的交点个数对于函数y=a x,其定义域为全体实数，值域为(0,+∞)。

指数函数与对数函数的交点
指数函数y=a x(a>0,a=1)与对数函数y=log a x(a>0,a=1)互为反函数，它们的交点问题一直让人困惑，是有一个交点，还是有两个交点，还是有更多的交点，一直是部分人争论的话题。

下面就此问题进行探究。

一个交点：一个交点的情况很普遍，可以随便找到一个实例比如a= 0.5，此时y=0.5x与y=log0.5x的交点是1个，其部分图像（仅画出了交点附近的图像）如图1：
图1:指数函数与对数函数有1个交点的情况
两个交点：两个交点的情况也比较好找，比如a=√
2，此时y=
(√
2)x与y=log√
2
x的交点是2个，其部分图像（仅画出了交点附近的图像）
如图2：
1
图2:指数函数与对数函数有2个交点的情况
三个交点：三个交点的情况比较少见，很难想到，此处给出一个实例，比如a=0.03，此时y=0.03x与y=log0.03x的交点是3个，其部分图像（仅
：
画出了交点附近的图像）如图3
2。