单级倒立摆稳定控制

单级倒立摆稳定控制摘要单级倒立摆是一种受控系统，在工业控制和机器人技术中有着广泛的应用。

这篇文档将介绍单级倒立摆的结构、原理和控制方法，特别是借助PID控制系统来实现单级倒立摆的稳定控制。

单级倒立摆是一种类人形机器人，它通常由一个水平旋转的轮子和一个通过电机传动的滑移杆组成，最后再由摆杆上的陀螺控制实现倒立。

这种结构使得单级倒立摆成为了机器人应用领域中的一个挑战问题。

为了实现单级倒立摆的稳定控制，需要在控制系统中引入一个合适的控制机制。

PID控制算法是一种最为通用的控制算法之一，常被用于像单级倒立摆这样的机器人平衡控制。

PID控制PID控制是一种基于反馈的控制系统，在工业和机器人技术中得到了广泛的应用。

PID控制通过比较实际的输出值与期望的输入值之间的差异，来作出对输出值的控制。

PID控制可以对输出值的稳定性、可靠性和精度进行控制，适用于不同类型的工业和机器人控制系统。

PID控制通常由三个部分组成：比例(P)、积分(I)和微分(D)控制。

比例控制反馈调整输出值，使得实际输出值逼近期望输入值。

积分控制记录过去所有误差，并将这些误差相乘来调整输出值。

微分控制通过记录过去的误差变化率，来防止输出值的快速变化。

在单级倒立摆稳定控制中，采用PID控制可以较好地解决因摩擦力、惯性、重心偏移等因素导致的系统不稳定问题，进而实现系统的平衡控制。

单级倒立摆的稳定控制实现单级倒立摆的稳定控制需要进行以下步骤：步骤1：系统建模将单级倒立摆系统建模，根据运动学和动力学原理，得到系统的运动方程。

步骤2：PID参数调节通过对PID控制算法中比例、积分、微分三个部分的参数进行调整，得到较好的控制效果。

步骤3：PID控制实现将PID控制器与单级倒立摆系统进行连接，实现单级倒立摆的稳定控制。

本文档介绍了单级倒立摆的结构、原理和控制方法，分析了PID控制算法在单级倒立摆稳定控制中的应用。

通过对步骤进行深入的解析，得到了单级倒立摆的稳定控制方法。

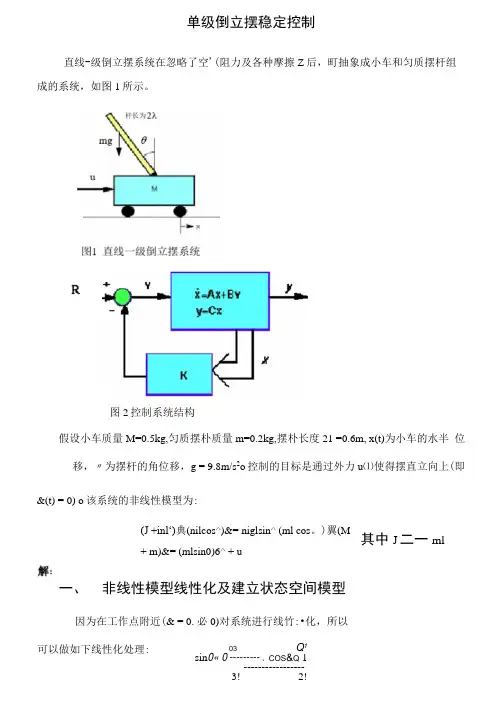
单级倒立摆稳定控制直线-级倒立摆系统在忽略了空'(阻力及各种摩擦Z后，町抽象成小车和匀质摆杆组成的系统，如图1所示。

图2控制系统结构假设小车质量M=0.5kg,匀质摆朴质量m=0.2kg,摆朴长度21 =0.6m, x(t)为小车的水半位移，〃为摆杆的角位移，g = 9.8m/s2o控制的目标是通过外力u⑴使得摆直立向上(即&(t) = 0) o该系统的非线性模型为:(J +inl‘)典(nilcos^)&= niglsin^ (ml cos。

)翼(M其中J二一ml+ m)&= (mlsin0)6^ + u一、非线性模型线性化及建立状态空间模型因为在工作点附近(& = 0.必0)对系统进行线竹:•化，所以可以做如下线性化处理: 03 Q1sin0« 0 --------- 、COS&Q 1-----------------3! 2!当e很小时，由COS0V sine的幕级数展开式可知，忽略高次项后, 可得cos0~l, sin0=0, 0Z 2=0：因此模型线性化后如下：(J+nil A2)0r z +mlx z z =mgl0 (a)取系统的状态变量为％ = x,x2 =仪X3 = x4=灰输出y = [x OF包扌舌小车位移和摆杆的角位移.由线性化后运动方程组得故空间状态方程如下:■010 0 ■「xT■ ■x2*00-2.6727 0x21 1.8182 x3f =000 1x3+0_x4J|_x40031.1818 0-4.5455uml0f r + (M+m) x''二u (b) 其中J = -ml3■ ■ xl ■ ■Xx2x1 x30 x4&Y=xlx3X1/二x'=x2—沁—册4(M + m) 一3m44(M + m) - 3m u3(M +m)g4(M + m)l 一3ni-34(M + m)l 一311119 1 00 ''xlM00 -3mg0am xl x2‘ _4(M + m) 一3m x2 x3* ~00 01x3x4J00 3(M + m)g0[_x44(M + m)l - 3ml 044(M + m) - 3m 0一34(M + m)l - 3nil二. 通过Matlab 仿真判断系统的可控与可观性，并说明其物理意义。

单级倒立摆三种控制方法的对比研究一、本文概述倒立摆系统作为经典的控制理论实验平台，被广泛用于研究和验证各种控制算法的有效性。

单级倒立摆作为倒立摆系统中最简单的形式，其动态特性和控制难度适中，成为了许多学者研究的焦点。

本文将重点探讨三种常见的单级倒立摆控制方法，并通过对比分析，揭示各方法的优缺点以及在不同场景下的适用性。

本文将简要介绍单级倒立摆的基本结构和动力学特性，为后续控制方法的研究奠定基础。

随后，将详细介绍三种控制方法：PID控制、模糊控制和最优控制，并阐述各自的基本原理和实现过程。

在此基础上，本文将通过仿真实验和实物实验，对比三种控制方法在单级倒立摆稳定控制中的表现，评估其控制精度、响应速度和鲁棒性等方面的性能。

通过本文的研究，旨在为倒立摆控制领域的研究者提供有益的参考，并为实际工程应用中的控制策略选择提供理论支持。

也希望本文的研究能够推动倒立摆控制技术的发展，为智能控制领域的发展做出一定的贡献。

二、单级倒立摆系统概述单级倒立摆系统是一种典型的非线性、不稳定、不可控系统，是控制理论研究和教学实验中常用的典型实验对象。

该系统由一个支点、一个摆杆和一个小球组成，摆杆一端通过支点与地面相连，另一端固定一个小球。

小球受到重力作用，会自然下垂，而摆杆则可以在垂直平面内自由摆动。

当系统受到外部扰动时，小球会偏离平衡点，导致摆杆摆动，系统变得不稳定。

单级倒立摆系统的控制目标是通过施加一定的控制力，使小球能够稳定地倒立在摆杆顶端，即保持系统平衡。

由于该系统具有非线性、不稳定和不可控等特性，控制难度较大。

为了实现这一控制目标，需要设计合适的控制器，并采用合适的控制策略。

在单级倒立摆系统的控制中，常用的控制方法包括PID控制、模糊控制、神经网络控制等。

PID控制是一种基于误差反馈的控制方法，通过不断调整控制量来减小误差，使系统达到稳定状态。

模糊控制则是一种基于模糊逻辑的控制方法，通过模糊化输入和输出变量，实现对系统的非线性控制。

单级倒立摆控制系统的稳定性算法设计张白莉【摘要】In order to control the balance of inverted pendulum, which has nonlinear, coupled, multivariable and unstable system, the mathematic model is made through lagrange equation, and the LQR controller is designed.Furthermore, the weighting matrix is optimized by the genetic algorithm and the superior parameters are obtained.The control results are simulated and analyzed through MATLAB.The experimental results show that LQR control is more effective and robust.%为了对一级倒立摆这个非线形、强耦合、多变量和自然不稳定系统的平衡性进行有效地控制,首先利用lagrange方程对系统进行了数学建模,设计了LQR控制器对其进行稳定性控制,并利用遗传算法优化加权矩阵,得出了比较理想的控制参数,最后利用Matlab对控制结果进行了仿真和分析.实验结果表明,LQR控制方法具有较强的鲁棒性和较好的控制效果.【期刊名称】《现代电子技术》【年(卷),期】2011(034)003【总页数】3页(P120-122)【关键词】倒立摆;LQR;Matlab;自动控制【作者】张白莉【作者单位】忻州师范学院物理电子系,山西,忻州,034000【正文语种】中文【中图分类】TN911-34;TP290 引言[1]倒立摆是日常生活中许多重心在上、支点在下的控制问题的抽象模型，本身是一种自然不稳定体，它在控制过程中能有效地反映控制中许多抽象而关键的问题，如系统的非线性、可控性、鲁棒性等问题。

倒立摆系统的控制算法及仿真1．1 倒立摆控制算法1．1．1 倒立摆控制算法概述单级倒立摆的稳定控制，实际上是一单输入多输出系统的稳定控制。

此时系统输入是电机控制电压u，输出是倒立摆竖直方向角度θ和旋臂位置ϕ。

对方程(2.5)进行变形即得θ与u 之间的输入输出方程,很明显,它是一个不稳定的二阶系统。

控制倒立摆使之稳定的方法很多,当前已有的倒立摆控制规律可总结为:(1)PID控制,通过对倒立摆物理模型的分析，建立倒立摆的动力学模型,然后使用状态空间理论推导出其非线性模型，再在平衡点处进行线性化得到倒立摆系统的状态方程和输出方程，于是就可设计出PID控制器实现其控制；(2)状态反馈H∞控制，通过对倒立摆物理模型的分析,建立倒立摆的动力学模型,然后使用状态空间理论推导出状态方程和输出方程，于是就可应用H∞状态反馈和Kalman 滤波相结合的方法,实现对倒立摆的控制；(3)利用云模型实现对倒立摆的控制，用云模型构成语言值,用语言值构成规则,形成一种定性的推理机制。

这种拟人控制不要求给出被控对象精确的数学模型，仅仅依据人的经验、感受和逻辑判断，将人用自然语言表达的控制经验,通过语言原子和云模型转换到语言控制规则器中，就能解决非线性问题和不确定性问题；(4)神经网络控制，业已证明神经网络(NeuralNetwork ,NN) 能够任意充分地逼近复杂的非线性关系，NN 能够学习与适应严重不确定性系统的动态特性，所有定量或定性的信息都等势分布贮存于网络内的各种神经元，故有很强的鲁棒性和容错性，也可将Q学习算法和BP神经网络有效结合，实现状态未离散化的倒立摆的无模型学习控制；(5)遗传算法( Genetic Algorithms , GA)，高晓智在Michine 的倒立摆控制Boxes 方案的基础上，利用GA 对每个BOX 中的控制作用进行了寻优，结果表明GA可以有效地解决倒立摆的平衡问题；(6)自适应控制，主要是为倒立摆设计出自适应控制器；(7)模糊控制，主要是确定模糊规则，设计出模糊控制器实现对倒立摆的控制；(8)使用几种智能控制算法相结合实现倒立摆的控制，比如模糊自适应控制，分散鲁棒自适应控制等等，(9)采用GA 与NN 相结合的算法，首先建立倒立摆系统的数学模型，然后为其设计出神经网络控制器，再利用改进的贵传算法训练神经网络的权值，从而实现对倒立摆的控制，采用GA 学习的NN 控制器兼有NN 的广泛映射能力和GA 快速收敛以及增强式学习等性能。

一级倒立摆数学模型一、啥是一级倒立摆嘿，小伙伴们！咱们来聊聊一级倒立摆这个有趣的玩意儿。

其实啊，一级倒立摆就是一个简单又神奇的系统。

想象一下，一根杆子，上面顶着个重物，然后这根杆子还能自由地转动。

咱们要研究的就是怎么让这个杆子不倒，还能稳定地保持平衡。

是不是感觉有点难理解？没关系，接着往下看！二、为啥要研究它你可能会问，研究这东西有啥用啊？这用处可大了去啦！它能帮助我们理解和控制很多不稳定的系统。

比如说走路、飞机的平衡控制，甚至是火箭的姿态调整。

通过研究一级倒立摆，咱们能掌握让这些复杂系统稳定运行的方法和技巧。

而且，这也是学习控制理论的一个很好的例子，能让我们更深入地理解那些抽象的数学概念。

三、数学模型咋建立好啦，重点来啦！咱们来说说怎么建立一级倒立摆的数学模型。

咱们得搞清楚这个系统的物理特性，像杆子的长度、重物的质量、转动的摩擦力等等。

然后，根据牛顿定律和一些数学知识，就能列出一堆方程啦。

这里面会涉及到微分方程、线性代数这些知识，可别被吓到哦！其实就是把物理现象用数学语言描述出来。

比如说，咱们可以用一个角度来表示杆子的倾斜程度，然后根据力和力矩的平衡关系，就能得到描述这个系统动态变化的方程。

当然，这只是个简单的介绍，真正的模型建立可要复杂得多，但只要咱们一步一步来，也能搞明白的！四、模型有啥特点这个数学模型有一些很有趣的特点哦！比如说，它是非线性的，这就意味着它不像咱们平时学的那些简单方程那么好处理。

而且，它对初始条件很敏感，一点点小的变化可能就会导致系统的行为完全不同。

不过，咱们可以通过一些方法，把它近似地转化为线性模型，这样就能用我们熟悉的控制方法来研究啦。

好啦，小伙伴们，关于一级倒立摆的数学模型就先讲到这里，希望大家能对它有个初步的认识和了解，要是感兴趣的话，还可以自己深入研究研究哦！。

单级倒立摆控制系统设计及simulink仿真摘要：倒立摆系统是一个典型的多变量、非线性、强藕合和快速运动的自然不稳定系统。

因此倒立摆在研究双足机器人直立行走、火箭发射过程的姿态调整和直升机飞行控制领域中有重要的现实意义，相关的科研成果己经应用到航天科技和机器人学等诸多领域。

单级倒立摆系统是一种广泛应用的物理模型。

控制单级倒立摆载体的运动是保证倒立摆稳定性的关键因素。

为了避免常用的物理反馈分析方法和运动轨迹摄像制导控制方法的某些缺点，本文从力学的角度提出对倒立摆的运动进行纯角度制导分析，完成了对倒立摆载体的角度制导运动微分方程的数学建模，设计了该模型的模糊控制系统，并利用 Matlab\simulink软件工具对倒立摆的运动进行了计算机仿真。

实验表明，这种模糊控制配合代数解析方法的运算速度和计算机仿真的效果均较物理反馈制导控制方法有了一定的提高。

该方法可以有效地改善单级倒立摆控制系统的性能。

本论文的主要工作是研究了直线一级倒立摆系统的模糊控制问题，用Matlab和Simulink对一级倒立摆模糊控制系统进行了仿真，验证了设计的可行性。

本文论述了一级倒立摆数学建模方法，推导出他们的微分方程，以及线性化后的状态方程。

讨论了单级倒立摆系统的模糊控制方法和操作步骤。

用Simulink实现了单级倒立摆模糊控制仿真系统，分别给出一级倒立摆系统控制量的响应曲线。

通过仿真说明控制器的有效性和实现性。

关键词：单级倒立摆；仿真；模糊控制；运动；建模；SimulinkDesign of single stage inverted pendulum control systemand Simulink simulationAbstract: inverted pendulum system is unstable system with a typical multi variable, nonlinear, strong coupled and fast motion. So the research on the attitude adjustment of the double foot robot and the attitude adjustment of the rocket launching process and the helicopter flight control field have practical,significance. The related scientific research achievements have been applied to many fields such as aerospace science and robotics. Single inverted pendulum system is a widely used physical model. Controlling the movement of the single inverted pendulum is the key factor to guarantee the stability of the inverted pendulum. In order to avoid some shortcomings of common physical feedback analysis method and motion trajectory camera guidance control method, this paper presents a pure angle guidance analysis on the motionof the inverted pendulum, and designs the fuzzy control system of the model. Experimental results show that the operation speed and computer simulation of this kind of fuzzy control combined with algebraic analysis method are improved by the physical feedback control method. This method can effectively improve the performance of a single stage inverted pendulum control system. In this paper, the main work of this paper is to study the fuzzy control of a linear inverted pendulum system, and the Matlab and Simulink to simulate the fuzzy control system of a single inverted pendulum, verify the feasibility of the design. And a mathematical modeling method of an inverted pendulum is described, their differential equations are derived, and the equation of state is linearized. The fuzzy control method and operation steps of single stage inverted pendulum system are discussed. Using Simulink to realize the fuzzy control simulation system of a single inverted pendulum, the response curve of the control of an inverted pendulum system is given. The effectiveness and the implementation of the controller are illustrated by simulation.Keywords: Inverted pendulum; Simulation; Fuzzy control; Motion; modeling; Simulink 引言倒立摆系统是研究控制理论的一种典型实验装置，具有成本低廉，结构简单，物理参数和结构易于调整的优点，是一个具有高阶次、不稳定、多变量、非线性和强藕合特性的不稳定系统。

基于拉格朗日建模的单级倒立摆起摆与稳定控制拉格朗日建模是一种经典的用来描述物体运动的数学方法。

倒立摆是一个典型的动态系统，在控制领域中有着广泛的应用。

通过拉格朗日建模可以描述单级倒立摆的运动方程，进而实现其起摆和稳定控制。

单级倒立摆由一个固定在支撑平面上的杆和一个可以沿杆轴旋转的质量小车组成。

杆的角度记为θ，小车的位置记为x。

首先，通过拉格朗日方程可以得到倒立摆的动力学方程：L = T - U其中，L为系统的拉格朗日函数，T为系统的动能，U为系统的势能。

对于单级倒立摆，可以将系统的动能和势能表示为：T = 1/2*m*ẋ^2 + 1/2*I*θ̇^2U = m*g*l*cos(θ)其中，m为小车的质量，I为杆的转动惯量，g为重力加速度，l为杆的长度。

ẋ和θ̇分别表示小车和杆的速度。

将动能和势能代入拉格朗日方程，即可得到系统的动力学方程：d/dt(∂L/∂ẋ) - ∂L/∂x = Fd/dt(∂L/∂θ̇) - ∂L/∂θ = 0其中，F为施加在小车上的外力。

经过计算，可以得到如下的方程：m*ẍ - m*l*θ̈*cosθ + m*l*θ̇^2*sinθ = FI*θ̈+ m*l*ẍ*cosθ - m*g*l*sinθ = 0这就是单级倒立摆的动力学方程，描述了杆的运动以及小车的受力等关系。

接下来，可使用控制理论中的各种控制方法，例如线性控制、非线性控制等，来实现单级倒立摆的起摆和稳定控制。

通过施加合适的控制输入F，使得杆保持在垂直位置附近，并稳定在指定的位置。

总之，基于拉格朗日建模的单级倒立摆起摆与稳定控制，通过分析系统的动能和势能，得到系统的动力学方程，然后使用控制理论中的方法进行控制设计，从而实现摆杆的起摆与稳定控制。

基于拉格朗日建模的单级倒立摆起摆与稳定控制1. 引言在探讨基于拉格朗日建模的单级倒立摆起摆与稳定控制之前，我们先来了解一下拉格朗日力学。

拉格朗日力学是一种研究物体运动的动力学方法，通过建立适当的广义坐标和拉格朗日函数，可以得到物体的运动方程。

倒立摆是一种典型的非线性控制系统，通过拉格朗日建模可以对其进行深入理解，从而实现稳定控制。

2. 基本概念拉格朗日力学的基本概念包括广义坐标、广义速度、拉格朗日函数等。

在单级倒立摆系统中，我们可以选取摆角作为广义坐标，角速度作为广义速度，通过拉格朗日函数可以描述系统的动力学行为。

在这里，我们要重点介绍拉格朗日方程，它是描述系统运动方程的核心。

3. 拉格朗日建模在单级倒立摆系统中，我们可以利用拉格朗日方程对系统进行建模。

我们需要确定系统的动能和势能函数，然后通过拉格朗日方程得到系统的运动学和动力学方程。

拉格朗日建模可以将系统的非线性特性充分考虑，从而更准确地描述系统的运动规律。

4. 单级倒立摆起摆单级倒立摆是一种经典的非线性控制系统，其起摆过程表现出了复杂的动力学行为。

在起摆过程中，系统需要克服重力和惯性力的作用，通过拉格朗日建模可以对系统的起摆过程进行深入分析。

在实际控制中，了解起摆过程的特点对于设计稳定控制很有帮助。

5. 稳定控制基于拉格朗日建模的单级倒立摆系统稳定控制是一个研究热点。

稳定控制的目标是使倒立摆在外部扰动的作用下能够保持平衡状态。

通过拉格朗日建模可以建立系统的控制方程，然后设计合适的控制器来实现稳定控制。

在稳定控制中，需要考虑系统的非线性特性和外部环境的影响，这就需要充分利用拉格朗日建模的优势。

6. 个人观点基于拉格朗日建模的单级倒立摆起摆与稳定控制是一个非常有挑战性的课题。

在研究和应用中，我认为需要充分理解拉格朗日力学的基本原理，深入掌握拉格朗日方程的推导和应用，同时结合倒立摆系统的动力学特性，才能够实现有效的稳定控制。

拉格朗日建模为我们提供了一种非常有力的工具，可以帮助我们更准确地描述和分析系统的动力学行为，从而实现高效稳定的控制。

单级倒立摆经典控制系统摘要：倒立摆控制系统虽然作为热门研究课题之一，但见于资料上的大多采用现代控制方法，本课题的目的就是要用经典的方法对单级倒立摆设计控制器进行探索。

本文以经典控制理论为基础，建立小车倒立摆系统的数学模型，使用PID控制法设计出确定参数(摆长和摆杆质量)下的控制器使系统稳定，并利用MATLAB软件进行仿真。

关键词：单级倒立摆；经典控制；数学模型；PID控制器；MATLAB 1绪论自动控制理论是研究自动控制共同规律的技术科学。

它的发展初期，是以反馈理论为基础的自动调节原理，并主要用于工业控制。

控制理论在几十年中，迅速经历了从经典理论到现代理论再到智能控制理论的阶段，并有众多的分支和研究发展方向。

1.1经典控制理论控制理论的发展，起于“经典控制理论”。

早期最有代表性的自动控制系统是18世纪的蒸汽机调速器。

20世纪前，主要集中在温度、压力、液位、转速等控制。

20世纪起，应用范围扩大到电压、电流的反馈控制，频率调节，锅炉控制，电机转速控制等。

二战期间，为设计和制造飞机及船用自动驾驶仪、火炮定位系统、雷达跟踪系统及其他基于反馈原理的军用装备，促进了自动控制理论的发展。

至二战结束时，经典控制理论形成以传递函数为基础的理论体系，主要研究单输入-单输出、线性定常系统的分析问题。

经典控制理论的研究对象是线性单输入单输出系统，用常系数微分方程来描述。

它包含利用各种曲线图的频率响应法和利用拉普拉斯变换求解微分方程的时域分析法。

这些方法现在仍是人们学习控制理论的入门之道。

1.2倒立摆1.2.1倒立摆的概念图1 一级倒立摆装置倒立摆是处于倒置不稳定状态，人为控制使其处于动态平衡的一种摆。

如杂技演员顶杆的物理机制可简化为一级倒立摆系统，是一个复杂、多变量、存在严重非线性、非自治不稳定系统。

常见的倒立摆系统一般由小车和摆杆两部分构成，其中摆杆可能是一级、两级甚至多级。

在复杂的倒立摆系统中，摆杆长度和质量均可变化。

直线一级倒立摆的自动起摆与稳摆控制（Simulink仿真）通过对倒立摆系统的力学及运动学分析，建立系统的非线性数学模型为可见，直线一级倒立摆为单输入双输出系统，利用Simulink可建立上式的框图模型，如图1所示。

图1 直线一级倒立摆系统的非线性Simulink模型倒立摆的起摆问题，是控制理论中的一个经典实验，其实质是倒立摆系统从一个稳定的平衡状态（垂直向下）在外力的作用下自动转移到另一个平衡状态（垂直向上）。

在这个过程中，要求起摆快速，但又不能过于超调。

由于输入、输出之间的非线性，许多常用的线性控制理论都不适用。

基于非线性理论，目前常用的几种起摆方法为：Bang-Bang控制、能量控制、仿人智能控制等。

这里采用Bang-Bang控制作为起摆方法，LQR控制作为稳摆方法，Simulink框图如图2所示。

图2 倒立摆自动起摆控制Simulink框图（Bang-Bang + LQR）图2中，子系统“Inverted Pendulum”是直线一级倒立摆的非线性模型，如图1所示；S函数“ang_proc”模块用于摆杆角度的处理，即将任意角度信号转换为“ -π ~ π”之间的对应值；子系统“Bang-Bang Controller”为Bang-Bang控制器；子系统“LQR Controller”为LQR 控制器。

双击“Bang-Bang Controller”模块可打开Bang-Bang控制器框图如下：图3 Bang-Bang控制器框图图3中，bang_controller是为实现Bang-Bang控制算法而编写的S函数，信号Ang_s是Bang-Bang控制切换角，F_bang是Bang-Bang控制作用力。

双击“LQR Controller”子系统，打开LQR控制器框图如下：图4 LQR控制器框图运行图2中的仿真框图，则基于Bang-Bang控制和LQR控制算法的直线一级倒立摆自动起摆控制效果如图5所示。

单级倒立摆稳定控制实验一．实验目的1.了解单级倒立摆的原理与数学模型的建立；2.掌握LQR控制器的设计方法；3.掌握基于LQR控制器的单级倒立摆稳定控制系统的仿真方法。

二．实验内容图1 一级倒立摆原理图一级倒立摆系统的原理框图如上所示。

系统包括计算机、运动控制卡、伺服机构、倒立摆本体和光电码盘几大部分，组成了一个闭环系统。

光电码盘1将连杆的角度、角速度信号反馈给伺服驱动器和运动控制卡，摆杆的角度、角速度信号由光电码盘2反馈回控制卡。

计算机从运动控制卡中读取实时数据，确定控制决策，并由运动控制卡来实现该控制决策，产生相应的控制量，驱动电机转动，带动连杆运动，保持摆杆的平衡。

在忽略了空气阻力，各种摩擦之后，可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统，如下图2所示。

图2直线一级倒立摆系统其中：M 小车质量 m 摆杆质量 b 小车摩擦系数l 摆杆转动轴心到杆质心的长度 I 摆杆惯量 F 加在小车上的力 x 小车位置φ摆杆与垂直向上方向的夹角θ摆杆与垂直向下方向的夹角（考虑到摆杆初始位置为竖直向下） 下图是系统中小车和摆杆的受力分析图。

其中，N 和P 为小车与摆杆相互作用力的水平和垂直方向的分量。

注意：在实际倒立摆系统中检测和执行装置的正负方向已经完全确定，因而矢量方向定义如图所示，图示方向为矢量正方向。

图3 （a ）小车隔离受力图； （b ）摆杆隔离受力图分析小车水平方向所受的合力，可以得到以下方程：MxF bx N =-- (1) 由摆杆水平方向的受力进行分析可以得到下面等式：()22sin d N m x l dtθ=+ (2)即：2cos sin N mxml ml θθθθ=+- 为了推出系统的第二个运动方程，我们对摆杆垂直方向上的合力进行分析，可以得到下面方程：()22cos d P mg m l dtθ-= (3)即：2sin cos P mg ml ml θθθθ-=-- 力矩平衡方程如下：sin cos Pl Nl I θθθ--= (4) 注意：此方程中力矩的方向，由于θπφ=+，cos cos φθ=-，sin sin φθ=-故等式前面有负号。