大学物理实验中不确定度计算的总结

i
姨 鄣鄣
% n
2
∑
i=1
鄣f 鄣Xi
UX
2
i
（9 ）
Ｐ ＝ ０． ６８３ １． ８４ １． ３２ １． ２０ １． １４ １． １１ １． ０９ １． ０８ １． ０７ １． ０６ １． ０５ １． ０３ １． ０２ １． ００ Ｐ ＝ ０． ９５ １２． ７ ４． ３０ ３． １８ ２． ７８ ２． ５７ ２． ４５ ２． ３６ ２． ３１ ２． ２６ ２． ２３ ２． ０９ ２． ０５ １． ９６ Ｐ ＝ ０． ９９ ６３． ７ ９． ９３ ５． ８４ ４． ６０ ４． ３０ ３． ７１ ３． ５０ ３． ３６ ３． ２５ ３． １７ ２． ８６ ２． ７６ ２． ５８
% %
Ux=S（x ）=
i
S （பைடு நூலகம் ）
I
作 为 不 确 定 度 的A类 评 定 ， 其 重 复 测 量 的 次 数 应 该 足 够 多 ，但 有 些 实 验 由 于 条 件 限 制 ，只 能 做 较 少 次 数 的 测 量 ，例 如 样本的理化参数会随着实验次数的增加而变化时 ， 就不宜多 次测量 。 测量次数少时 ， 由上式算出的标准偏差可能会被严重 低估 ， 这时应采用基于 t 分布确定的包含因子来表示 A 类不确 定度 ， 也称扩展不确定度 。 即
UB=
（7 ） K 其中 K 是仪器误差概率分布的置信系数 。 虽然存在各种分
△仪
布类型 ， 但在大学物理实验中比较常见的有三种分布 ， 即正态 分 布 、 矩 形 分 布 （ 均 匀 分 布 ）、U 形 分 布 。 其 置 信 系 数 分 别 为 3 、
% n 2
S （x ）=
i
如果以 n 次测量的平均值作为测量结果 ， 则其算术平均值 的标准偏差为

大学物理实验教学中关于实验数据的不确定度的计算和分析作者：孙红章王翚苏向英来源：《教育教学论坛》2015年第35期摘要：本文首先讨论了大学物理实验教学中关于不确定理论中的直接测量量的A类、B类标准不确定度和合成不确定度以及间接测量量的不确定度的通常表示方法，随后推算出了几个基本物理实验中各个测量量不确定度的计算公式，对大学本科学生的物理实验教学具有指导意义。

关键词：大学物理实验教学;不确定度计算;固体密度测量;杨氏弹性模量测量;共轭法测凸透镜焦距中图分类号：G642 ; ; 文献标志码：A ; ; 文章编号：1674-9324（2015）35-0169-02现如今在大学物理实验教学中为了更加准确和精确的表示实验测量结果，常使用不确定度理论来表示实验测量结果。

[1，2]在大学物理实验教学中，不确定度的计算一直是一个难点，也是一个重点，许多本科学生因为不确定度的计算方法非常复杂，而且计算量很大，而放弃对实验数据的科学处理。

这里我们将阐述大学物理实验教学中不确定度的通常表示方法，并结合有关的基本物理实验，在课堂上用多媒体演示，使大学一年级学生很容易掌握不确定度的计算，取得了良好的教学效果。

一、不确定度理论的一般原理和计算方法[3，4]不确定度理论对于直接测量量把数据的不确定度根据数据的性质来分类，把符合正态分布统计规律的称之为A类标准不确定度，而不符合正态分布统计规律的称之为B类标准不确定度。

把两类不确定度的平方和的根称之为测量量的合成标准不确定度，或者简称为不确定度。

大学物理实验中物理量的直接测量量的平均值的标准偏差即为A类标准不确定度，它的计算公式为：t的大小与物理量的测量次数n和置信概率p有关系，置信概率p一般约定取值为68.3%，特殊情况下置信概率p取95.4%。

如果我们测量9次，置信概率取p=68.3%，那么置信因子取t=1.07。

如果我们测量5次，置信概率取p=68.3%，置信因子取t=1.14。

产生原因：
仪器误差 方法误差 环境误差 人为误差
.
8
1. 系统误差
仪器误差
天平不等臂所造成的
系统误差
.
9
方法误差
内接
VR
VA
A
外接
IR A
V
用V作为VR的近似值 时，求
R V VR VA
I
I
VR VA VR I II
V IV
RV I
V V
I R IV I R
.
10
环境误差
输入
市电的干扰
不确定度
1、不确定度的定义 “由于测量误差的存在而对被测量量值不 能肯定的程度，是具有一定置信概率的误 差估值的绝对值”
对测量值的准确程度给出一个量化的表述。
x 测量结果x＝ Δ （单位）
不确定度Δ值可以通过一定的方法估算。
.
18
2、测量结果的表达（报告）方法
测量结果的科学表达方法：
XX（单位）
E 8 .9 0 0 .0 7% 4 0 1 .00 g /c 33 m 6
（5）密度测量的最后结果为
8.900 7.00(g 3c6m 3)
四、实验数据的有效位数
对没有小数位且以若干个零结尾的数值， 从非零数字最左一位向右数得到的位数 减去无效零（仅为定位用的零）的个数， 就是有效位数；
对其他十进位数，从非零数字最左一位 向右数而得到的位数，就是有效位数。
设n次测量结果为x1,x2,xn的误差为 i
由
1 n
n i
1
xi
a n
n i
i
可知
在确定的测量条件下可增加测量次数减小
随机误差，多次测量的算术平均值可作为

饼图
展示整体的构成比例，适用于 显示各部分在整体中的占比。
EXCEL软件在数据处理中的应 用
EXCEL软件功能强大，是数据处理中不可或缺的工具。它能轻松处理各种类型 的数据，并可创建图表进行数据可视化。
EXCEL拥有丰富的公式和函数库，可用于数据分析和计算。它还提供了数据透 视表和数据透视图，方便用户进行数据探索和分析。
视觉美观和易读性
图表的颜色、字体和布局要和谐 统一，避免过多的装饰，保证图 表的清晰易读。
常用的数据绘图类型
折线图
显示数据随时间或其他变量的 变化趋势，适用于展示数据变 化的趋势和规律。
柱状图
用于比较不同类别的数据，适 合显示各类别之间的差异和大 小。
散点图
显示两个变量之间关系，用于 探索数据之间的关联性和趋势 。
结论和思考题
1 1. 总结
本次课程学习了物理实验测量 的不确定度及数据处理的基本 知识，掌握了常见误差类型、 误差估计方法和数据处理技巧 ，为今后开展物理实验打下了 基础。
2 2. 思考
在实际实验中，如何更有效地 控制误差，提高测量结果的准 确度？
3 3. 探索
除了本课程所涉及的知识，还 有哪些测量不确定度及数据处 理方法可以学习？
重复测量法
对同一物理量进行多次测量，然后计算平均值和标准偏差来估计误差。
间接测量误差估计
间接测量是指通过已知物理量之间的关系来计算未知物理量，例如用速度和时 间计算距离。
误差传播公式
通过误差传播公式，可以将已知物理量的误差传播到计算结果中，从而估计间 接测量结果的误差。
重复测量误差估计
重复测量
1
多次测量同一个物理量，得到一组数据。
数据绘图的基本要求

数据：
直径 D (mm)
12
四、 间接测量结果及不确定度的计算 设间接测量的函数关系式为： N＝f (x ，y ，z……)，
其中x ，y ，z为相互独立的直接测量量， N为 间接测量量 。
设x, y, z，的不确定度分别为△x 、 △y 、 △z ， 它们必然影响间接测量结果，使N也有相应的 不确定度△N
改为N= (2.80±0.08) ×104cm
改为N= (10.7±0.2) cm
N= (10.651±0. 12) cm 改为N= (10.6±0.2) cm
29
例：用米尺测长方形边长，测得以下数据： (单位： cm) a=1.99; 2.02; 2.01; 2.00; 1.97; 2.00 b=5.57; 5.59; 5.55; 5.49; 5.48; 5.54 求：长方形面积S.
②乘除法 结果的有效数字位数与诸数中有效数字位数最少者 相同。
③乘方，开方 结果的有效数字位数与自变量的有效数字位数相同。
④对数
(1)自然对数的有效数字位数与真数的有效数字位 数相同。
例： Ln5.374=1.682
20
(2)以10为底的对数，其尾数的有效数字 位数与真数的有效数字位数相同。 例： Lg15.0=1. 176
7
(2)多次测量 N趋于无穷时， 服从正态分布, 而进行有限次测量，一般服从t分布(学生分布)。
大学物理实验中n 的次数一般不大于10次 , 在5＜n≤10时，作△A＝Sx近似，置信概率p为0.95 或更大。所以作为简化计算， 可直接把Sx 的值当作 测量结果的总不确定度的A类分量△A。
若n不在此范围或要求更高，用公 式(6)
⑤常数,π,e 等有效数字位数可认为是无限的。但一 般取比运算各数中有效数字位数最多的还多一位。

大物实验不确定度计算公式
在大物实验中，不确定度是一个非常重要的概念。

不确定度可以理解为测量结果与真实值之间的差异，它是一个用来描述测量精度的指标。

在实验中，我们需要计算出每个测量值的不确定度，以便更好地评估实验结果的可靠性和精确性。

下面是大物实验中常用的不确定度计算公式：
1. 算术平均值的不确定度：
其中，n表示测量次数，Δx表示每次测量值与平均值之差，s
表示样本标准差。

2. 直接测量值的不确定度：
其中，δ表示仪器误差，Δ表示读数误差，L表示仪器量程。

3. 复合测量值的不确定度：
其中，u表示单个元件的不确定度，σ表示元件间的相关系数。

在实验过程中，我们需要根据实际情况选择合适的不确定度计算公式，并根据公式计算出每个测量值的不确定度。

同时，我们还要注意将不确定度传递至最终结果中，以便更好地评估实验的可靠性和精确性。

- 1 -。

北方民族大学物理实验中心 Fundamental physics experiment
6
1、合成不确定度
u ( x) u u
2 A
2 B
(k 1)
＊各不确定度相互独立 扩展不确定度
U ( x) ku( x)
2、测量结果的不确定度表示
x u ( x) （单位） P …
u ( x) E ( x) 100 % x
在某一数值u范围内，用公式表示为：
N N0 u
（置信概率为P）
其中u值可以通过一定的方法进行估算，称为不 确定度。
北方民族大学物理实验中心 Fundamental physics experiment
3
N N0 u
（置信概率为P）
测量的不确定度也可以理解为测量误差可能出现 的范围，标示着测量结果的可靠程度。如果不确定度 越大，则测量结果可靠性差，应用价值低，反之，则 测量结果的可靠性好，应用价值大。
Uy
Uy yEy
北方民族大学物理实验中心 Fundamental physics experiment
21
1、间接测量量的最佳值
直接测量量
x, y , z , 的 最佳值为 x , y , z ,
N f ( x , y, z ,)
北方民族大学物理实验中心 Fundamental physics experiment
其中：直接测量量x、y、z…的不确定度分别是
：
ux、uy、uz ux、uy、uz
则，间接测量量N的不确定度 量的不确定度
uN 是由直接测量
传递而来。
北方民族大学物理实验中心 Fundamental physics experiment

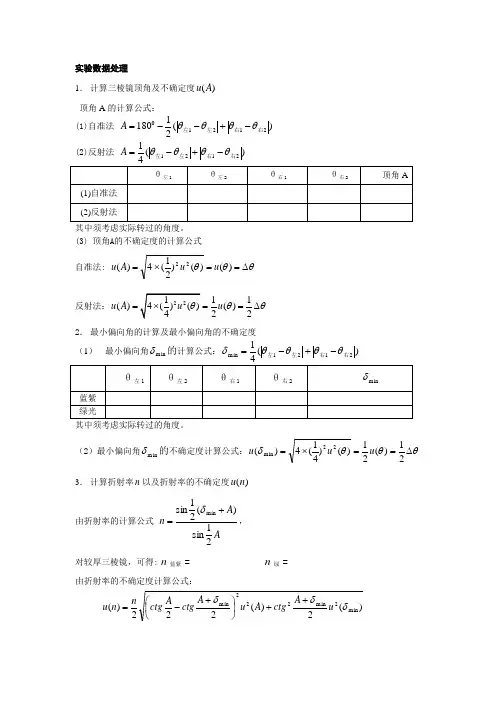
实验数据处理1． 计算三棱镜顶角及不确定度)(A u 顶角A 的计算公式： (1)自准法 )(211802121右右左左θθθθ-+--=A (2)反射法 )(12121右右左左θθθθ-+-=A其中须考虑实际转过的角度。

(3) 顶角A 的不确定度的计算公式 自准法: θθθ∆==⨯=)()()21(4)(22u u A u反射法：11()()22u A u θθ===∆2． 最小偏向角的计算及最小偏向角的不确定度 （1） 最小偏向角min δ的计算公式：)(12121min 右右左左θθθθδ-+-=（2）最小偏向角min δ的不确定度计算公式：θθθδ∆==⨯=21)(21)()41(4)(22min u u u3． 计算折射率n 以及折射率的不确定度)(n u由折射率的计算公式 A A n 21sin )(21sin min +=δ，对较厚三棱镜，可得: n蓝紫= n 绿 =由折射率的不确定度计算公式：)(2)(222)(min 2min222min δδδu A ctgA u A ctg A ctg n n u ++⎪⎭⎫ ⎝⎛+-=)()21sin(2)(21cos )()21(sin 2)21sin(min 22min 222min δδδu A A A u A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡= 22min 222min )21()21sin(2)(21cos )()21(sin 2)21sin(θδθδ∆⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++∆⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=A A A 仪器误差 Δθ = 2′= 5.82×10-4(rad)可得:u (n 蓝紫) = ，u (n 绿) =测得折射率n 蓝紫= ± ，n 绿 = ±数据处理注意事项与角度的不确定度有关的数值的单位应取为弧度。

Page 10 of 16
中山大学理工学院、东校区实验中心编制
实验编号及题目：
《大学物理实验》课程实验报告纸
院系：工学院 姓名：刘广 学号：11309018 日期：2012 年 4 月 20 号
砝码质量为 10g~90g 时：
砝码质量 天平示值
100 99.9
200 199.9
300 299.9
400 399.8
1
1
标准差������������ = √10×9 × ∑10 (������������ − ������)2 = {90 × [(44.5 − 44.53)2 + (44.5 − 44.53)2 + (44.6 − 44.53)2 + ������=1
(44.5 − 44.53)2 + (44.5 − 44.53)2 + (44.5 − 44.53)2 + (44.5 − 44.53)2 + (44.6 − 44.53)2 + (44.5 − 44.53)2 + (44.6 − 44.53)2 ]} = 2 × 10−2 (������) 又有������ =
1
深度：ℎ = 10 × ∑10 ℎ������=10 ×(3.863+3.860+3.887+3.869+3.865+3.868+3.870+3.8723.864+3.873) ������=1
=
1 10 1
×38.691=3.8691 (cm)
1
质量：������ = 10 × ∑10 ������������=10 ×(44.5+44.5+44.6+44.5+44.5+44.5+44.5+44.6+44.5+44.6) ������=1

根据解析几何知识判断图线的类型由图线类型判断公式可能的特点确定公式的形式63实验数据处理的基本方法若自变量作等间隔变化时测得另一物理量看做函数一系列对应的值为了从这一组实验数据中合理的求出自变量改变引起的函数值的改变即它们的函数关系通常把测量数据前后对半分成一二两组用第二组的第一项与第一组的第一项相减第二组的第二项与第一
▪ 期末考试占0--30%
实验须知
▪ 学生在规定的时间内进行实验，不得无故旷 课和迟到。无故迟到10分钟者，不得进入实 验室。
▪ 进入实验室，保持室内安静和整洁，不得大 声喧哗。
▪ 对安排的实验要有预习报告，提交教师审阅， 对没有预习报告者，不得进入实验室做实验。
实验须知
▪ 认真完成本组实验，不得擅自搬动和使用其 他组的仪器和物品。
操作读数时的视差影响。
特点：
①小误差出现的概率比大误差出现的概率大；
②多次测量时分布对称，具有抵偿性——因此取多次测量的平 均值有利于消减随机误差。
随机变量的分布
正态分布：大量相对独立因素共同作用下得到的随机变量服
从正态分布。物理实验中多次独立测量得到的数据一般可以近似
看作服从正态分布
p(x)
1
范围内的概率很大， 的取值与一定的概率相联系。）
测量
▪ 测量分为直接测量和间接测量
直接测量指无需对被测的量与其它实测的量进行函数关系的 辅助计算而可直接得到被测量值的测量；
间接测量指利用直接测量的量与被测量之间的已知函数关系 经过计算从而得到被测量值的测量
1.2.3 等精密度测量 在同等条件下进行的多次重复性测量称为等密精度测
x u
0.683
x u2
0.954
x u3
0.997

150 mm 500 mm 1000 mm
125 mm
1 mm 1 mm 1 mm
0.02 mm 0.05 mm 0.01 mm
±0.10 mm ±0.15 mm ±0.20 mm
±0.02 mm ±0.05mm ±0.004 mm
游标卡尺 螺旋测微器（千分尺）
0～25 mm
七级天平（物理天平）
500g
测量的误差和不确定度
• 测量是物理实验的基础。
• 测量结果应包括数值、单位和对测量结果精确程度的
评价（不确定度）。
以电阻测量为例
R＝910 .3 0.4
测量对象 数值 不确定度 单位
含义： R 的真值有相当大（例如95%）的可能（概率） 位于区间 （909.9，910.7）Ω 之内。
•
测量分为直接测量和间接测量
d (8.345 8.348 8.344 8. 343 8.347 8.344)/6 8.345mm
d 8.345-(-0.003) 8.348mm
(2)计算A类不确定度
d
d
n 1
i
d

2
n(n 1)
0.002mm
(3)计算B类不确定度
测量结果的有效位数越多，其相对不确定度越小，精确度越高
例：0.0123与1.23与123的有效位数都是3位。0.01230有效位数是4位,
最右边的“0”是有效位数，不可以省略不写。
科学记数法
记
例1：
A a 10 , 且1 a 10
n
光速C=30万公里每秒
不正确的写法：C=300000km/s；C=30km/s 正确的写法：C=3.0×105km/s=3.0×108m/s

出的
,
取 其最 小分 度值 为该直 尺 的误差 极 限
,
。
以伏 安
法 测 电阻 实验 所 测量 得 到 的 实验 数 据进 行说 明 图 关系图
。
是 根 据表
伏 安法 测 电 阻 的 数据 表格 作
作者 简介
范士 民
大 学物 理 实验
一
,
男
一
,
实验 师
,
享 阳 师 范 学 院 物 理 与 电 子 科 学学 院 研 究 方 向
・
・
” “
,
电流
的不 确定 度
声,
声又
,
根 据 电压 电流 求得 的相 应 的不 确 定度
可 以计 算 出 电阻
的不 确定度
一
一
第六 居 全 目 龙等 李谈 物 搜 实 脸 教 李研 衬 奋伦 大 票
产,
・
下
红
产
一
、
,
。
测 量 结果 的 正 确表 述
士产
. 士 0 4 6 ) x l o ’( 。 )
k
(
。)
. 4 2 逐 差 法不 确定 度 的 评定
结 合相 关系 数 r 的 表 达 式
,
可 以求 出相 应 的
. 声 (k ) = 2 9 4 6 x 10
r = 0 9993365 .
一,
(
。
一
,
)
一 117一
第六 居 令 田 龙等 嵘教 物 理 实 脸 散 学研 付 套伦 文 集 ( 下 )
第六 居 个 日 龙等 檬谈 物 理 实脸教 檬研 讨 套伦 次 集
下
常用 三 种 方 法 处 理 实验 数 据 结 果 的 不 确 定 度 评定

的拐点
x2 x1
pxdx
σ小 σ大
x
ξ表示随机变量 x 在〔x1，x2〕区间出现的概率，称为置信概率。
实际测量的任务是通过测量数据求得μ 和σ的值。
lim
n
xi
n
lim n
xi 2
n
x x2 x3
0.683 0.954 0.997
大学物理实验误差理论
14
随机变量的分布
• 实际测量次数有限，可用 n 次测量值的x、sx 来估算μ、σ:
x
i 1
n 1
σx大，表示测得值很分散，随机误差分布范围宽，测量的精密度低；
σx小，表示测得值很密集，随机误差分布范围窄，测量的精密度高；
σx可由带统计功能的计算器直接求出。
大学物理实验误差理论
11
随机误差的处理举例
例：用50分度的游标卡尺测某一圆棒长度L，6次测量 结果如下（单位mm）： 120.08,120.14,120.06, 120.10, 120.06, 120.10
则：测得值的最佳估计值为
LL12.0 09 mm
测量列的标准偏差
L
n
(Li L)2
i1
n1
0.03mm
大学物理实验误差理论
12
测量误差与不确定度
• 不确定度的权威文件是国际标准化组织(ISO)、国际
计量局(BIPM)等七个国际组织1993年联合推出的
Guide to the expression of Uncertainty in measurement
《大学物理实验》不确定度 基础知识
大学物理实验误差理论
1
主要内容
1 测量误差和不确定度估算的基础知识 2 实验数据有效位数的确定 3 作图法处理实验数据 4 数据的直线拟合（最小二乘法处理实验数据）

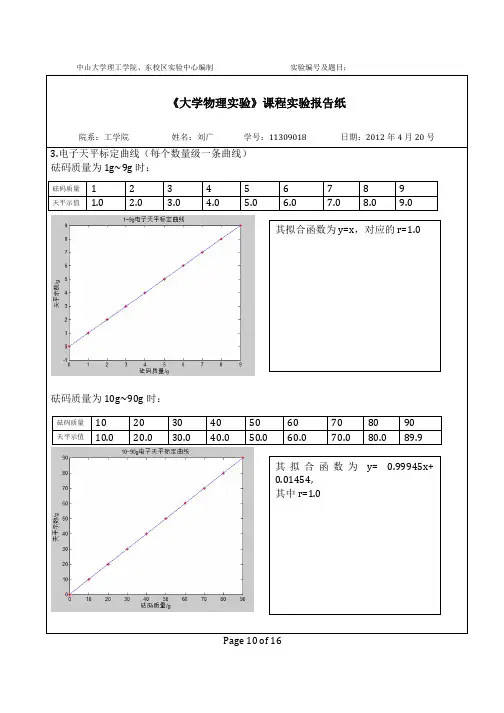
大学物理实验系列分光计的调整与使用参考答案 LELE was finally revised on the morning of December 16, 2020用分光计测量三棱镜折射率实验数据处理1.顶角及不确定度)(A u 的计算(1)自准法: )(2118021210右右左左θθθθ-+--=A ， θθθ∆==⨯=)()()21(4)(22u u A u (2)反射法： )(412121右右左左θθθθ-+-=A 2.最小偏向角及最小偏向角的不确定度的计算（1）最小偏向角min δ的计算公式：)(412121min 右右左左θθθθδ-+-= （2）最小偏向角min δ的不确定度计算公式：θθθδ∆==⨯=21)(21)()41(4)(22min u u u 仪器误差Δθ = 2′= ×10-4(rad)u (A ) = 2′= ×10-4(rad) u (δmin ) = 1′= ×10-4(rad)A = ° ′±2′ δmin = ° ′±1′3.折射率n 以及折射率的不确定度)(n u 的计算(1)折射率的计算公式 A A n 21sin )(21sin min +=δ (2)折射率的不确定度计算公式)(2)(222)(min 2min 222min δδδu A ctg A u A ctg A ctg n n u ++⎪⎭⎫ ⎝⎛+-= )(2sin 2cos 21)(2sin 2sin 2cos 212cos 2sin 21min 22min 222min min δ⎪⎪⎪⎪⎭⎫ ⎝⎛δ++⎪⎪⎪⎪⎭⎫ ⎝⎛δ+-δ+=u A A A u A A A A A )()21sin(2)(21cos )()21(sin 2)21sin(min 22min 222min δδδu A A A u A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=22min 222min )21()21sin(2)(21cos )()21(sin 2)21sin(θδθδ∆⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++∆⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=A A A 式中的角度的不确定度应取弧度为单位 n ±u (n ) = ±思考题及参考答案1.望远镜光轴与分光计的中心轴相垂直，应该在望远镜中看到什么现象利用哪些螺钉调节光学平行平板或三棱镜两个光学面反射的十字像，都能与望远镜分划板叉丝刻线上交点重合。

测量者的估算误差Δ估
测量者对被测物或对仪器示数判断的不确定性会产生估算误差Δ估。对于有刻度的仪器仪表，通常Δ估为最小刻度的十分之几，小于Δ仪（因为最大允差已包含了测量者正确使用仪器的估算误差）。比如，估读螺旋测微器最小刻度的十分之一为0.001毫米，小于其最大允差0.004毫米；估读钢板尺最小刻度的十分之一为0.1毫米，小于其最大允差0.15毫米。但有时Δ估会大于Δ仪。比如，用电子秒表测量几分钟的时间，测量者在计时判断上会有0.1-0.2秒的误差。而电子秒表的稳定性为10-5秒/天，显然仪器的最大允差小得实在可以忽略。又如第30届国际物理奥林匹克竞赛实验题中要测量一个摆杆的质心到一端的距离。将摆杆放到一个“⊥”型物上并使之平衡，测量支撑点到摆一端的距离。由于“⊥”型物棱宽为2mm，摆杆在棱上移动±1mm均能保持平衡，使得一次测量的估算误差应为±1mm，大于钢直尺的最大允差Δ仪=0.15mm。在拉伸法测金属丝杨氏模量实验中，由于难以对准金属丝被轧头夹住的位置，钢丝长度的估算误差可达±（1-2）mm。在暗室中做几何光学实验，进行长度测量时，长度的估算误差也可达±（1-2）mm。如果Δ估和Δ仪是彼此无关的，B类不确定度ΔB为它们的合成：
测量的不确定度和数据处理
测量不确定度
采用不确定度的必然性
国际计量局等七个国际组织于1993年指定了具有国际指导性的“测量不确定度表示指南ISO 1993（E）”（以下简称《指南》）。几年来国际与国内的科技文献开始采用不确定度概念，我国各个高校也不断开展这方面的讨论，改革教学内容与方法，以求与国际接轨。虽然一些学者对《指南》的有些内容持批评态度[注1]，但总的趋势是在贯彻《指南》的同时，不断改善它。
对于不是线性关系的物理规律，拟合曲线比较麻烦；由曲线求解实验方程的参数也比较困难。有时可以对物理量进行适当变换，按变换后的的物理量作图，把曲线改成直线，就方便处理了。现在，很多商品计算器对于线性、对数、指数和幂函数关系都具有回归计算功能，只需按相应的键就可以拟合这些函数关系。实验数据处理方法也应“与时俱进”，充分享用新技术带给人类的方便。有必要让我们的学生掌握这些方法。

3.3 10 3 mm
UA (d )
tp
s(d ) n
2.36 3.3103 8
2.7 103 mm
（4）计算B类不确定度：仪器误差取最小分度值的一半， 即Δm ＝0.005mm，因此
UB (d ) m 0.005 mm
（5）合成不确定度：
U(d)
U
2 A
(d
)
U
2 B
(d
)
2.7 103 2 5 103 2 5.7 103 0.006 mm
F
x1
2 u ( x1 )
F
x2
2 u(x2 )
...
F xk
2 u(xk )
注意：
（a） 当F= F(x1,x2,…xk)为乘除或方幂函数关系时， 可以先将求对数，再求导。
（b） 本式只适于各变量互相独立的情形，若不独立 则
例如：f比=较xy复2.杂，求超u(出f)本=?书范围。
ln f ln x 2 ln y
。
2）标准不确定度的 B类评定( uB )
是指用非统计方法评定的不确定度，如用经验或资料以 及假设的概率分布估计出的不确定度与未定系统误差有 关的分量，用估计的标准偏差表示。
uB
(x)
m (x) k
m (x)为仪器的最大允许误差限，而包含因子k由可能的误差概率分布决
定：按正态分布、均匀分布和三角分布，分别取 3、 3 、 6 。
注意：m：仪器误差限, 指测量仪器的示值与真值之差的最大值。
一般实验中, 对于刻度仪器仪表, m常取最小分度值的1/2， 大多数遵循均匀分布，所以K取 3 。
③标准不确定度合成（C类不确定度）（uC ）： 也称合成标准不确定度

高等教育17学法教法研究课程教育研究在大学物理实验课程中，我们在完成了一组测量之后，应该如何给出测量的最终结果呢？这结果当中当然应该包括测量值，还应该包含反映测量的精确程度的量。

由于任何测量都有可能包含多种误差，误差的大小就标志了测量的精确程度，所以最终结果中还要包含对误差大小的评估。

但是，我们无法确定每次具体测量的误差。

注意到误差的综合作用引起了测量值的分散，我们可以对测量结果的分散性给出某种定量的描述。

这种描述测量值分散范围的量，我们称为不确定度u 。

[1-2]一、不确定度和误差的异同不确定度u 和误差Δ是两个不同的概念。

误差∆是测量值和真值的差别。

不确定度u 表征的是被测量的真值所处量值的分散范围，表示由于误差的存在而对被测量不能确定的程度。

不确定度u 越小，测量的精确程度越高。

最终结果表达的表达形式测量一个物理量x ，最终结果表达式的形式应当如式（1）所示。

x=±u（1）式（1）表示物理量x 真值的最佳估计值是，而区间（-u ，+u ）以很大的可能性包含了真值。

如果仅做了单次测量，那么可以用单次测量值来代替。

我们常把称为测量值。

例如，我们测量重力加速度g ，最终结果必须表示成式（2）的形式。

g=（9.7±0.2）m/s 2（2）给出测量值当然是重要的。

最佳估计值与真值μ的接近程度要比标准差S 小1⁄倍，所以我们在结果中要明显地指出测量值。

如果我们仅用区间（-u ，+u ）来表示测量结果，例如g=（9.5，9.9）m/s 2，就达不到这样的效果。

二、不确定度的意义我们更有必要来强调一下给出不确定度u 的重要性。

很多时候，科学实验不仅仅只是关心测量值，而是为了测试一种理论，或者为了和其他实验结果作比较，或者为了预言另一个实验的结果。

[3]例如，我们测量重力加速度，不只是关心重力加速度是多大。

也许是希望和去年几十公里外的某地计量部门给出的结果g=（9.81±0.01）m/s 2作比较，来看看引力常数G 在这几年里是否有变化，或者我们附近是否有一个能影响重力加速度的大金矿，或者地球是否不再自转了（虽然有更简单的方法来确定这一点），或者自然界是否有一种新的相互作用力使得单摆的周期与地形有关？如果你的测量值是9.70m/s 2，那么有3种可能情况：第一种可能，不确定度u=0.15m/s 2，即g=（9.70±0.15）m/s 2，这与g=（9.81±0.01）m/s 2是相符的。