当前位置：文档之家 › 材料力学梁的弯曲变形第4节 简单超静定梁

材料力学梁的弯曲变形第4节 简单超静定梁

  • 格式：ppt
  • 大小：500.50 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

材料力学-弯曲变形

材料力学-弯曲变形

(向下)
qB
qmax
w(l)
Pl 2 2EI
(顺时针)
例题2
图示的等截面简支梁长为l，抗弯刚度为
EI，在右端受有集中力偶M0的作用，求梁任
一截面的转角和挠度。
y
解:
由整体平衡得 FAx=0， FAy= FBy= M0/l 从而，截面的弯矩为
M(x)= xFAy= xM0/l
FAx A x o
FAy
横截面变形：
线位移：长度变化
水平方向—小变形假定，挠曲轴平坦，忽略不计 垂直方向—挠度 w= w(x)
转角：角度变化
横截面相对于原位置转过的夹角，
一般用q (x)表示截面转角，并且以逆时针为正
q'
对于细长梁，略去剪力对变形影响 平截面假设成立: 变形的横截面与挠曲轴垂直
q q tan q dw
(l 2
a2)
y
例题3
P x
A
C
于是，梁的挠曲线方程为 FAx
l
w
w1 w2
(x) (x)
0 xa a xb
FAy
a
b
Pb
6 EIl
Pa
6 EIl
x3 (b2 l2 )x (l x)3 (a2 l2
)(l
x)
0 xa a xl
转角方程为
q w ww12((xx))
0 xa a xb
Pb 2EIl
x2
C1
ቤተ መጻሕፍቲ ባይዱdx
Pb 6EIl
x3
C1x
D1
同理，对CB段
w2
w2dx C2
Pa EIl
(l
x)dx
C2

材料力学-简单的超静定问题

材料力学-简单的超静定问题

2021/6/16
4
2021/6/16
5
2021/6/16
6
§6-2 拉压超静定问题
拉压变形时的胡克定律 l FN l EA
综合考虑变形的协调条件、虎克定律和静力 学平衡条件求解拉压超静定问题。
2021/6/16
7
例 已知1、2杆抗拉刚度为E1A1, 3杆抗拉刚度为E3A3， F的大小已知，求各杆内力。
13
2
l
A
A*
l3
FN 3l E3 A3
9
4、联解方程
FN1
2 cos
F
E 3 A3
E 1 A1 c o s 2
FN 3
1
2
F E 1 A1
cos3
E 3 A3
2021/6/16
10
装配应力的计算：超静定结构中由于加工误 差， 装配产生的应力。
平衡方程：
FN1 FN2
F N 3(F N 1F N 2)cos
超静定问题：若未知力的个数多于独立的平
衡方程的个数，仅用静力平衡方程便无法确定
全部未知力，这类问题为超静定问题。相应结
构称为超静定结构。
2021/6/16
2
超静定次数：未知力个数与独立平衡方程数之 差，也等于多余约束数。
多余约束：在结构上加上的一个或几个约束， 对于维持平衡来说是不必要的约束称多余约束。 对应的约束力称多余约束反力。
由于超静定结构能有效降低结构的内力及变 形，在工程上应用非常广泛。
2021/6/16
3
基本静定系：解除多余约束代之于未知力后的 结构。
●超静定问题的解法：综合考虑变形的几何相 容条件、物理关系和静力学平衡条件。

材料力学 简单的超静定问题

材料力学 简单的超静定问题
l1 F N 1l1 E 1 A1
FN 3 l 3 E 3 A3
FN1
FN3
a a A
A1 FN2
l3
FN 3l3 E 3 A3
(3)
(4)补充方程：由几何方程和物理方程得：
F N 1l1 E1 A1
2

cos a
(5)联解（1）、（2）、（3）式，得:
FN 1 FN 2 E1 A1 F cos a 2 E1 A1 cos a E 3 A3
第六章
简单的超静定问题
1
第六章
§6-1
§6-2
简单的超静定问题
超静定问题及其解法
拉压超静定问题
§6-3 §6-4
扭转超静定问题 简单超静定梁
2
§6-1
超静定问题及其解法
1.单纯依靠静力平衡方程能够确定全部未知力（支反 力、内力）的问题，称为静定问题。 相应的结构称为静定结构。
2.单纯依靠静力平衡方程不能确定全部未知力（支反 力、内力）的问题，称为超静定问题。 相应的结构称为超静定结构。
3
F N3 A3 9F 14 A [ ]
F
[F ]
14 9
14 9
[ ] A
[ ] A
11
[例6-2-4]木制短柱的四角用四个40404的等边角钢 加固，角钢和木材的许用应力分别为[]1=160MPa和 []2=12MPa，弹性模量分别为E1=200GPa 和 E2 =10GPa；求许可载荷P。 解：（1）以压头为研究对象, 设每 个角钢受力为FN1，木柱受力为FN2.
14
B
1
D
C
3 2
(2) 几何方程
l1 ( l 3 ) cos a

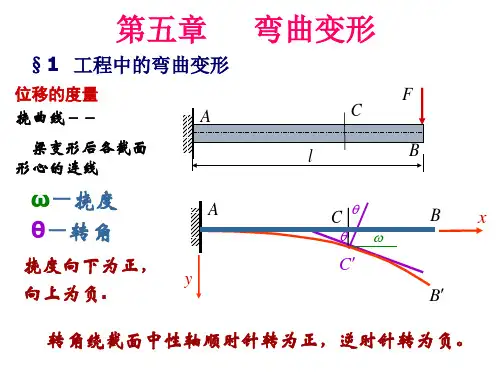
材料力学第5章弯曲变形ppt课件

材料力学第5章弯曲变形ppt课件

qL
4.22kNm
4.22kNm
M
max
32 M
max
76.4MPa
WZ
d 3
例题
20kN m
A
4m
FA
20kN m
A
MA
4m
试求图示梁的支反力
40kN
B
D
2m
2m
B
B1 FB
FB 40kN
B
D
B2
2m
2m
在小变形条件下,B点轴向力较小可忽略不
计,所以为一次超静定.
C
B1 B2
FBBBMF12AA2383qFEqELBqqLI84LI2LLZZ32F35BFF4FEFB83PBPLIEL7Z3L12IZ.218352.k75N5kFkN2PNmEL2IZ2
x
边界条件
A
L2
B
L2
C
y
连续条件
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
全梁仅一个挠曲线方程
C
q
EA
共有两个积分常数 边界条件
L1
A
x
B
EI Z
L
y
例题 5.5
用积分法求图示各梁挠曲线方程时,试问在列各梁 的挠曲线近似微分方程时应分几段;将分别出现几个 积分常数,并写出其确定积分常数的边界条件
q
a
B C LBC
B
2a
FN
B
q2a4
8EIZ
FN 2a3
3EIZ
C
FN
a
D

材料力学——4梁的弯曲内力

材料力学——4梁的弯曲内力

21
例题1 图所示，悬臂梁受集中力F作用， 试作此梁的剪力图和弯矩图 解： 1.列剪力方程和弯矩方程
FQ ( x) F
(0＜x＜l ) (0≤x＜l)
M ( x) Fx
2.作剪力图和弯矩图 由剪力图和弯矩图可知：
FQ M
max max
F Fl
22
例题 2简支梁受均布荷载作用，如图示， 作此梁的剪力图和弯矩图。 解：1.求约束反力 由对称关系，可得： 1 FAy FBy ql 2 2.列剪力方程和弯矩方程
Q2 Q1– Q2=P
x
x
梁的内力计算的两个规律：
（1）梁横截面上的剪力FQ，在数值上等于该截 面一侧（左侧或右侧）所有外力在与截面平行方 向投影的代数和。即：
FQ
F
yi
若外力使选取研究对象绕所求截面产生顺时针 方向转动趋势时，等式右边取正号；反之，取 负号。此规律可简化记为“顺转剪力为正”， 或“左上，右下剪力为正”。相反为负。
12
二、例题
[例1]：求图（a）所示梁1--1、2--2截面处的内力。 q 2 解：截面法求内力。 qL 1 1--1截面处截取的分离体 1 a y qL A M1 x1 Q1 图（b） 2 b 如图（b）示。
x
图（a）
Y qL Q1 0 Q1 qL
mA( Fi ) qLx1 M1 0 M1 qLx1
作梁的剪力图 FQB右=4kN/m×2m=8kN，FQD=0
34
35
27
3. 弯矩图与剪力图的关系
(1)任一截面处弯矩图切线的斜率等于该截面 上的剪力。 (2) 当FQ图为斜直线时，对应梁段的M图为二 次抛物线。当FQ图为平行于x轴的直线时，M图 为斜直线。

工程力学第10章 弯曲变形与简单超静定梁

工程力学第10章 弯曲变形与简单超静定梁

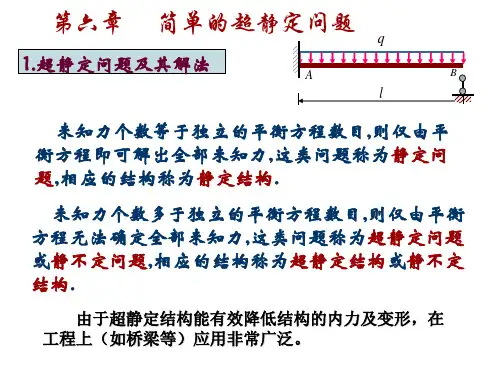
简支梁。 根据原超静定梁A端横截面转角θA=0这一变形条件, 即可进而建立补 充方程以求解MeA。 建议读者按此自行算出全部结果。 以上解题的方法步骤也适用于解二次超静定梁。 此时可建立两个变形几何方程, 因而补充方程也就有两个。 这样, 解多余约束力时就需解二元一次联立方程组。 对于三次以上的超静定梁若仍用上述方法求解, 则将不够简便, 此时就宜采用其 他方法。
但弹性模量E值则是比较接近的。 2.调整跨度 梁的转角和挠度与梁的跨度的n次方成正比, 跨度减小时, 转角和挠度就会有更 大程度的减小。 例如均布载荷作用下的简支梁, 其最大挠度与跨度的四次方成 正比, 当其跨度减小为原跨度的1/2时, 则最大挠度将减小为原挠度的1/16。 故减小跨度是提高梁的刚度的一种有效措施。 在有些情况下, 可以增设梁的中 间支座, 以减小梁的跨度, 从而可显著地减小梁的挠度。 但这样就使梁成为超 静定梁。 图10-10a、 b分别画出了均布载荷作用下的简支梁与三支点的超静 定梁的挠曲线大致形状, 可以看出后者的挠度远较前者为小。 在有可能时, 还 可将简支梁改为两端外伸的梁。 这样, 既减小了跨度, 而且外伸端的自重与两 支座间向下的载荷将分别使轴线上每一点产生相反方向的挠度(图10-11a、 b), 从而相互抵消一部分。 这也就提高了梁的刚度。 例如桥式起重机的桁架钢梁 就常采用这种结构形式(图10-11c), 以达到上述效果。
下述关系
因为挠曲线为一平坦的曲线, θ值很小, 故有 tanθ≈θ(c) 由式(b)、式(c)两式可见, 梁横截面的转角应为
式(d)表明转角θ可以足够精确地从挠曲线方程(a)对x求一次导数得到。 它表 示梁横截面位置的x与该截面的转角θ之间的关系, 通常称为转角方程。 在图10-2所示的坐标系统中, 挠度w以向上为正, 向下为负; 转角θ则以逆时针 转向为正, 顺时针转向为负。

材料力学


5 Pa RD a RD a 6 EI 3EI 3EI
如何得到？
A D
P
B
自行完成
C D
RD
例题 6
图示结构AB梁的抗弯刚度为EI，CD杆的抗拉刚度为EA，
已知P、L、a。求CD杆所受的拉力。
D
a
A
C
L
2
L
B
2
P
解：变形协调条件为 wC lCD
D
a
C
FC
A
( P FC ) L wC 48EI FC L lCD EA
温度应力：
FB E t A
6 1 12 . 5 10 碳素钢线胀系数为 C0
温度应力：超静定结构中，由于温度变化，使构
件膨胀或收缩而产生的附加应力。
不容忽视！！！
路、桥、建筑物中的伸缩缝 高温管道间隔一定距离弯一个伸缩节
例题 11
图示阶梯形杆上端固定，下端与支座距离=1mm， 材料的弹性模量E=210GPa，上下两段杆的横截 面面积分别为600平方毫米和300平方毫米。试 作杆的轴力图。
C
A
FA
B
L2
FC
FA FB FC qL 0
L2
M
A
0
FB
变形协调方程
L qL2 FC FB L 0 2 2
3 FB qL 16
FA 3 qL 16
C q C FC 0
7.5kNm
5qL4 FC L3 5 0 FC qL 8 384 EI Z 48EI Z
由于超静定结构能有效降低结构的内力及变形，在 工程上（如桥梁等）应用非常广泛。
●超静定问题的解法：

材料力学考研复习资料第4章弯曲内力


M eb l
发生在C截面右侧
思考：对称性与反对称性
FA
F
FB
A
B C
l/2
l/2
Fs
F/2
x
F/2
x
M
Fl/4
FA
Me
FB
A
B C
l/2
l/2
Fs
Me l
x
Me/2
M
Me/2
x
结论：
• 结构对称、外力对称时，弯矩图为正对称， 剪力图为反对称
• 结构对称、外力反对称时，弯矩图为反对称， 剪力图为正对称
34
A1 2
34
Bx
内力
FS M
1—1 -P -Pa
2—2 2P -Pa
3—3 2P Pa
4—4 2P -2Pa
3、在集中力作用处，剪力值发生突变，突变值= 集中力大小；
在集中力偶作用处，弯矩值发生突变，突变值= 集中力偶矩大小。
例 图示简支梁受到三角形分布荷载的作用，最大荷
载集度为q0，试求截面C上的内力。
1 FS1
M1 Fa ( 顺 )
截面2—2
Fy 0 FS2 FA F 0
F
C2 2 M2
FA 2 FS2
FS2 FA F 2F MC2 0 M2 F a 0
M 2 Fa ( 顺 )
y
Me =3Fa
F
1A2 3 4
B
1 2 34
x
a
a
FA
2a
FB
截面3—3 F
C33 M3
1 8
ql
FSB左
1 ql 8
剪力方程为常数，剪力图为
水平线。
M图：

材料力学 弯曲变形PPT课件


EIw ql x3 - q x4 Cx D 12 24
(3) 利用边界条件确定积分常数
x 0: w0 D0 x l : w 0 C ql3
24
(4) 求转角方程、挠度方程 EIw ql x q x2 0 x l
22
w q l3 6lx2 4x3
转角方程
EI为常量 EIw [ M (x)dx] dx Cx D 挠度方程
C、D 为积分常数；由边界条件和连续性条件确定。
边界条件: 固定端：w＝0；θ＝0；
铰支座：w＝0；
弯曲变形的对称点：θ＝0。
连续性条件: 挠曲线上任意点的挠度和转角只有一个
值。
[例7-3-1]用积分法求挠度方程和转角方程，并确定绝
第七章 弯曲变形
第七章 弯曲变形
§7.1 概述 §7.2 挠曲线的近似微分方程 §7.3 用积分法求挠度和转角 §7.4 用叠加法求挠度和转角 §7.5 梁的刚度计算 §7.6 简单超静定梁 §7.7 梁的弯曲应变能 §7.8 提高弯曲刚度的措施
§7-1 概述
一、工程中的弯曲变形问题
若变形过大，会引起较大的振动，破坏起吊工 作的平稳性。
又如，车床主轴：
若变形过大，不 仅会影响齿轮的 啮合和轴承的配 合，使传动不平 稳，磨损加快， 而且还会严重地 影响加工精度。
4
又如，如图所示轮轴： 若轮轴的变形过大，会使轮子不能正常啮合，影响工 作的平稳性等。
5
但有时又有相反要求，要求构件有适当变形，才能 符合使用要求。
如汽车叠板弹簧，要求产生较大变形，才能在车辆 行驶时发挥缓冲减振作用符合使用要求。
24EI
w
q
w qx l3 2lx2 x3

梁弯曲变形的计算


yC 2
A MA FA A F C
(a)
Fl 3 24 EI Z
B FB B FB
求得有无顶尖作用时，在刀 尖处变形比为：
yC 7 yC 2 32
结论：可见用顶尖可有效地 减小工件的变形，因而，在 细长轴加工中要设置顶尖， 甚至使用跟刀架。
材料力学
+ A C F B
(b)
F MA A 2a (a)
2
x
d y 2 dx
d y M ( x) 所以 2 dx EI z
2
O
1
2
M (x ) < 0
dy dx 2 < 0
2
x
材料力学
由弯矩的正负号规定可得，弯矩的符号与挠曲 线的二阶导数符号一致，所以挠曲线的近似微分方 程为：
d w M ( x) 2 dx EI z
由上式进行积分，就可以求出梁横截面的转角 和挠度。
1 M ρ EI z

忽略剪力对变形的影响
1 M ( x) ( x) EI z
材料力学
由数学知识可知：
d y 2 1 dx dy 2 3 [1 ( ) ] dx 略去高阶小量，得
2
y M (x ) > 0 M (x ) > 0
dy dx 2 > 0 O
y M (x ) < 0
3
11ql 3 ( ) 48EI
材料力学
wC
例4 已知：悬臂梁受力如图 示，q、l、EI均为已知。求C 截面的挠度wC和转角C 解 1）首先，将梁上的载荷变成 有表可查的情形
为了利用梁全长承受均 布载荷的已知结果，先将均 布载荷延长至梁的全长，为 了不改变原来载荷作用的效 果，在AB 段还需再加上集 度相同、方向相反的均布载 荷。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

补充方程
yB 0
ql4 Fl3 0 8EI 3EI
（5）求解多余约束力 F 3 ql (1) 8
（6）列方程求 A 处支反力
n
Fix 0
i 1
n
Fiy 0
i 1
n
M A (Fi ) 0
i 1
FAx 0
( 2)
FAy F ql 0 (3)
i 1
n
M A (Fi ) 0
i 1
FAx 0
联
FAy F1 F2 0
立 求
M A F1a F2l 0 解
+
F2

F1 2
a3 l3
(3
l a
1)
即 可
注意 多余约束的选取并不是唯一的，只要是维持 平衡额外的约束，都可以视为多余约束，也就是说相 当系统可以有不同的选择。
求解静不定梁的关键在于确定多余约束反力，其 方法和步骤可概述如下：
• 根据约束反力与独立平衡方程的数目，判断梁的静 不定次数；
• 解除多余约束，以相应的多余约束力代替其作用， 得到原静不定梁的相当系统；
• 计算相当系统在多余约束处的位移，并由相应的变 形协调条件建立补充方程，由此求出多余支反力。
例6-8 梁的约束如图，承受均布载荷 q 作用，试
yB yB1 yB2 0
力F1单独作用时，查表 6-1 得
yB1


F1a 2 6EI
(3l

a)
力F2单独作用时，查表 6-1 得
yB2

F2l 3 3EI
代入变形协调条件得
+
F2

F1 2
a3 l3
(3 l a
1)
• 用静力学平衡方程求解
n
Fix 0
i 1
n
Fiy 0
MA

ql 2 2

Fl

0
( 4)
联立求解即可
FAx 0
FAy

5ql 8
MA

ql 2 8
（7）画剪力图和弯矩图
FS ( x)

5ql 8

qx
M (x) ql2 5ql x 1 qx2 88 2
例6-9 例 6-8 中，若 q 10 kN/m ，l 8 m，材料
求约束力 F 、FAx、FAy
力图和弯矩图。
，以及约束力偶（1）梁的静不定次数 梁是一次静不定梁
（2）选择相当系统
（3）在相当系统上计算解 除约束处的变形
yB yBq yBF
查表
yBq

ql4 ， 8EI
yBF

Fl3 3EI
+
（4）将相当系统与原静不定梁的变形进行比较，列出
• 将原来的超静定梁在形式上
转力变F2成共在同载作荷用下F1和的多静余定未悬知臂
梁，称为原静不定梁的相当 系统。
• 为了使相当系统和原超静定 梁相同，要求在多余约束处 必须符合超静定梁的变形协 调条件。
在本例中
yB 0
+
• 现在利用叠加法求图示梁的 B 点的挠度。
• 超静定梁的变形协调条件：
• 超静定梁：在工程中，有时为了提高粱的强度和刚 度，或由于构造上的需要，会给静定梁增加约束， 于是，梁未知约束力（支反力）的数目就超过了静 力学平衡方程的数目，某些约束力不能完全由静力 学平衡方程求出，这就是静不定梁，或者称为超静 定梁。
静不定次数 = 未知约束力总个数 独立平衡方程数
• 多余约束：在静定梁上增加的约束，对于维持构件 平衡来说是多余的，因此，常把这种对维持构件平 衡并非必要的约束称为多余约束。与多余约束所对 应的支座反力或反力偶，统称为多余约束反力。

667 cm3
查 B-3 表 28a 槽钢
表 WZ 340 cm3
（2）考虑梁自重影响
查表得 28a 槽钢理论重量为 31.427 kg/m，如果考 虑槽钢自重，则二根槽钢
qG 2 31.427 9.8 N/m 0.6154 kN/m
由弯矩方程和弯矩图
M max

(q qG )l 2 8
许用应力 [ ] 120 MPa ，选用两根热轧普通槽钢组
成如示截面梁，试选择槽钢型号。
（1）不考虑梁自重的影响； （2）考虑梁自重的影响。
解：（1）不考虑梁自重影响
由弯矩方程和弯矩图
M max

ql 2 8
80 kN m
两根槽钢组成的截面梁，要求其抗弯截面系数
2WZ

M max
[ ]
静不定次数 = 未知约束力总个数 独立平衡方程数
• 超静定梁的求解方法：与求解轴向拉压超静定问题
类似，为了求解静不定梁，除列出静力平衡方程式
外，还需要变形协调条件以及力与位移间的物理关
系，建立的补充方程个数应与静不定次数相等，这
样才能解出全部约束反力。
解除多余约束，以
举例说明分析静不定梁的解法 多余未知力F2 代替
84.9 kN m
两根槽钢组成的截面梁，要求其抗弯截面系数
2WZ

M max
[ ]

708 cm3
查 B-3 表 28b 槽钢
表 WZ 366 cm3