材料力学-梁弯曲时的位移
- 格式:ppt
- 大小:3.64 MB
- 文档页数:99

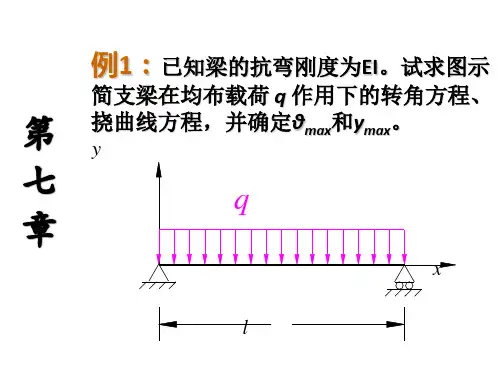
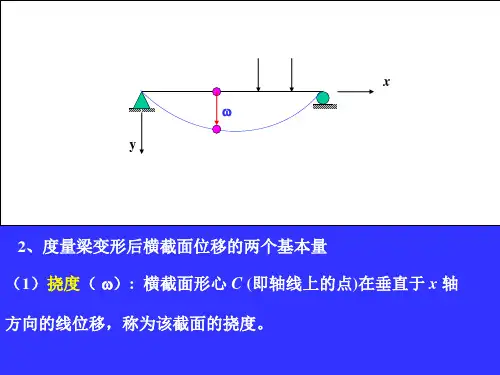




梁的最大位移计算公式梁的最大位移计算公式是用于计算梁在受力作用下发生的弯曲位移的公式。
梁是指在两个支点之间受力作用的一种结构。
梁的最大位移是指梁在受力作用下最大弯曲的位移值。
梁的位移计算涉及到材料力学和结构力学的知识,其中梁的形状、材料特性、受力情况等都会对最大位移的计算产生影响。
在计算梁的最大位移时,一般可以使用梁的弯曲理论来进行计算。
梁的弯曲理论可以通过假设梁是一根弯曲曲线的理论来进行推导。
根据弯曲理论,可以得到梁的最大位移计算公式。
δmax = (5 * Pl^4) / (384 * E * I)其中,δmax表示梁的最大位移;P表示梁上的受力值;l表示梁的长度;E表示梁所采用的材料的弹性模量;I表示梁的截面惯性矩。
这个公式是根据梁的弯曲理论推导得到的,可以用于计算梁在受力作用下的最大位移。
在使用这个公式进行计算时,需要知道梁的受力情况、几何形状和材料特性。
其中,受力情况包括梁上所受到的力和力的位置;几何形状包括梁的长度和截面形状;材料特性包括梁所采用的材料的弹性模量和截面惯性矩。
需要注意的是,这个公式是基于一些简化假设和梁的边界条件推导得到的,只适用于一些特定的情况。
在实际应用中,可能需要考虑更多的因素,如梁的支点、梁的侧向刚度、梁的动态响应等。
因此,在具体应用中需要根据实际情况,结合可能的简化假设和合适的分析方法进行位移计算。
总之,梁的最大位移计算公式用于计算梁在受力作用下的最大弯曲位移,其中涉及到梁的几何形状、受力情况和所采用的材料特性。
使用这个公式进行计算时,需要根据实际情况进行合理的简化和假设,并结合适当的分析方法来进行计算。




材料力学(土)笔记第五章 梁弯曲时的位移1.梁的位移——挠度及转角为研究等直梁在对称弯曲时的位移取梁在变形前的轴线为x 轴,梁横截面的铅垂对称轴为y 轴而xy 平面即为梁上荷载作用的纵向对称平面梁发生对称弯曲变形后,其轴线将变成在xy 平面内的曲线1AC B度量梁变形后横截面位移的两个基本量是挠度:横截面形心(即轴线上的点)在垂直于x 轴方向的线位移ω转角:横截面对其原来位置的角位移θ 梁变形后的轴线是一条光滑的连续曲线,且横截面仍与该曲线保持垂直因此横截面的转角θ也就是曲线在该点处的切线与x 轴之间的夹角度量等直梁弯曲变形程度的是曲线的曲率梁的变形还受到支座约束的影响通常就用这两个位移量来反映梁的变形情况梁轴线弯曲成曲线后,在x 轴方向也将发生线位移 但在小变形情况下,梁的挠度远小于跨长,梁变形后的轴线是一条平坦的曲线横截面形心沿x 轴方向的线位移与挠度相比属于高阶微量,可略去不记因此在选定坐标后,梁变形后的轴线可表达为()f x ω=式中,x 为梁在变形前轴线上任一点的横坐标;ω为该点的挠度梁变形后的轴线称为挠曲线,在线弹性范围内,也称为弹性曲线上述表达式则称为挠曲线(或弹性曲线)方程由于挠曲线为一平坦曲线,故转角θ可表达为''tan ()f x θθω≈== 称为转角方程即挠曲线上任一点处的切线斜率'ω可足够精确地代表该点处横截面的转角θ 由此可见,求得挠曲线方程后,就能确定梁任一横截面挠度的大小,指向及转角的数值 正值的挠度向下,负值的挠度向上正值的转角为逆时针转向,负值的转角为顺时针方向2.梁的挠曲线近似微分方程及其积分为求得梁的挠曲线方程,利用曲率κ与弯矩M 间的物理关系,即 1M EIκρ== 式中曲率κ为度量挠曲线弯曲程度的量,是非负的这是梁在线弹性范围内纯弯曲情况下的曲率表达式在横力弯曲时,梁横截面上除弯矩M 外尚有剪力S F 但工程用梁,其跨长l 一般均大于横截面高度的10倍剪力S F 对于梁位移的影响很小,可略去不计,故该式子依然适用式中的M 和ρ均为x 的函数,即1()()()M x x x EIκρ== 在数学中,平面曲线的曲率与曲线方程导数间的关系有'''23/21()(1)x ωρω=±+ 取x 轴向右为正,y 轴向下为正时曲线凸向上时''ω为正,凸向下时为负而按弯矩的正、负号规定,梁弯曲后凸向下时为正,凸向上为负,符号相反于是得到 '''23/2()(1)M x EIωω=-+ 由于梁的挠曲线为一平坦曲线,因此,'2ω与1相比十分微小可以略去不计故上式可近似的写为 ''()M x EIω=-上式略去了剪力S F 的影响,并略去了'2ω项 故称为梁的挠曲线近似微分方程若为等截面直梁,其弯曲刚度EI 为一常量,上式可改写为''()EI M x ω=-对于等直梁,上式进行积分,并通过由梁的变形相容条件给出的边界条件确定积分常数 即可求得梁的挠曲线方程当全梁各横截面上的弯矩可用单一的弯矩方程表示时,梁的挠曲线近似微分方程仅有一个 将上式的两端各乘以dx ,经积分一次,得'1()EI M x dx C ω=-+⎰再积分一次,即得12[()]EI M x dx dx C x C ω=-++⎰两式子中积分常数1C 、2C 可通过挠曲线的边界条件确定例如在简支梁中,左右铰支座处的挠度均等于零在悬臂梁中,固定端处的挠度和转角均等于零确定积分常数1C 、2C 后,就分别得到梁的转角方程和挠曲线方程从而可以确定任一横截面的转角和挠度1C 和2C 的几何意义 由于以x 为自变量,在坐标原点即0x =处的定积分恒等于零因此,积分常数'100x C EI EI ωθ===,20C EI ω=式中,0θ和0ω分别表示坐标原点处截面的转角和挠度若梁上的荷载不连续即分布荷载在跨度中间的某点处开始或结束,以及集中荷载或集中力偶作用处梁的弯矩需分段写出,各段梁的挠曲线近似微分方程也随之不同在对各段梁的近似微分方程积分时,均将出现两个积分常数为确定这些积分常数,除需利用支座处的约束条件外还需利用相邻两段梁在交界处位移的连续条件例如左、右两段梁在交界处的截面应具有相等的挠度和转角不论是约束条件和连续条件,均发生在各段挠曲线的边界处故均成为边界条件,即弯曲位移中的变形相容条件遵循两个原则①对各段梁,都是从同一坐标原点到截面之间的梁段上的外力列出弯矩方程所以后一段梁的弯矩方程包括前一段的弯矩方程的新增的()x a -项②对()x a -项的积分,以()x a -作为自变量于是由x a =处的连续条件,就能得到两段梁上相应的积分常数分别相等的结果 对于弯矩方程需分为任意几段的情况,只要遵循上述规则同样可以得到各梁段上相应的积分常数分别相等的结果从而简化确定积分常数的运算3.按叠加原理计算梁的挠度和转角梁在微小变形条件下,其弯矩与荷载成线性关系 在线弹性范围内,挠曲线的曲率与弯矩成正比当挠度很小时,曲率与挠度间呈线性关系梁的挠度和转角均与作用在梁上的荷载成线性关系在这种情况下梁在几项荷载(如集中力、集中力偶或分布力)同时作用下某一横截面的挠度或转角 就分别等于每项荷载单独作用下该截面的挠度或转角的叠加,即为叠加原理 已知梁在每项荷载单独作用下的挠度和转角表则按叠加原理来计算梁的最大挠度和最大转角将较为方便4.奇异函数·梁挠曲线的初参数方程5.梁的刚度校核·提高梁的刚度的措施5.1 梁的刚度校核对于梁的挠度,其许可值通常用许可挠度与跨长之比值[]l ω作为标准 梁的刚度条件可表达为 max[]ll ωω≤ max []θθ≤ 一般土建工程中的构件,强度要求是主要的刚度要求一般处于从属地位但当对构件的位移限制很严,或按强度条件所选用的构件截面过于单薄时刚度条件也可能起控制作用5.2 提高梁的刚度的措施由梁的位移表可见梁的位移(挠度和转角)除了与梁的支承和荷载情况有关还与其弯曲刚度EI 成反比,与跨长l 的n 次幂成正比减小梁的位移,可采取下列措施①增大梁的弯曲刚度EI②调整跨长和改变结构5.梁内的弯曲应变能当梁弯曲时,梁内将积蓄应变能梁在线弹性变形过程中弯曲应变能V ε在数值上等于作用在梁上的外力所作的功W梁在纯弯曲时各横截面上的弯矩M 为常数,并等于外力偶矩e M当梁处于线弹性范围内e EI EI θρ=== θ与e M 呈线性关系直线下的三角形面积就代表外力偶所作的功W ,即12e W M θ=从而得纯弯曲时梁的弯曲应变能 12e V M εθ=即得2222e M l M l V EI EIε== 横力弯曲时,梁内应变能包含两个部分:与弯曲变形相应的弯曲应变能和与切应变形相应的剪切应变能对于弯曲应变能,取长为dx 的梁段,其相邻两横截面的弯矩应分别为()M x 和()()M x dM x +在计算微段的应变能时,弯矩的增量为一阶无穷小,可略去不计 计算器弯曲应变能为2()2M x dV dx EIε= 全梁的弯曲应变能则可通过积分求得为2()2l M x V dx EIε=⎰ 式中,()M x 为梁任一横截面上的弯矩表达式 当各段梁的弯矩表达式不同时,积分需分段进行梁的剪切应变能远小于弯曲应变能,可略去不计。
关于梁的弯曲中若干公式的分类讨论①梁的弯曲是指受力作用下梁的截面发生了形变,弯曲应力和弯曲变形会对梁的使用性能产生影响。
因此,研究梁的弯曲是很重要的。
在梁的弯曲研究中,涉及到若干公式,我们可以对这些公式进行分类讨论。
一、力学公式力学公式是描述梁的弯曲情况时经常用到的公式,包括以下几个方面:1. 矩形截面梁的抗弯极限状态当梁受到弯曲力矩时,梁截面内部产生由受力引起的应力,如果应力超过了材料所能承受的极限值,则梁就会发生断裂。
矩形截面梁的抗弯极限状态公式是:M=1.5×f_y×Z_x,其中M代表弯曲力矩,f_y代表截面所使用的钢材的抗拉强度,Z_x代表梁截面的抗弯截面模量。
2. 矩形薄壁截面梁的端部弯曲应力当梁受到弯曲力作用时,端部的弯曲应力有时比较集中,这种情况在矩形薄壁截面梁中比较常见。
矩形薄壁截面梁的端部弯曲应力公式是:σ_max=Mc/I,其中σ_max代表端部的最大弯曲应力,M代表弯曲力矩,c代表截面厚度,I代表截面惯性矩。
3. 梁内应力分布公式如果梁内部应力分布不均匀,就会导致梁的强度变化,因此要研究梁内应力分布。
梁内应力分布公式是:σ=My/I+zQ_x,其中σ代表应力,M代表弯曲力矩,y代表截面中心到离截面上缘距离,I代表截面惯性矩,z代表离截面上缘距离,Q_x代表梁截面的剪力。
1. 梁位移公式梁的位移指梁在弯曲时最大的偏移距离,梁位移公式是:δ=5WL^4/384EI,其中δ代表梁的最大位移,W代表梁的承载能力,L代表梁的长度,E代表梁材料的弹性模量,I代表截面对弯曲的惯性矩。
2. 切线旋转公式切线旋转公式用来描述梁在弯曲中切线和轨迹的关系,切线旋转公式是:Ψ=ML/2IEI,其中Ψ代表角度,M代表弯曲力矩,L代表梁的长度,I代表截面对弯曲的惯性矩,EI代表弹性模量与截面惯性矩的乘积。
材料力学公式用来描述材料在弯曲状态下的性质变化,涉及以下几个方面:1. 摆动强度公式摆动强度公式是表示材料在弯曲状态下疲劳寿命的公式,摆动强度公式是:S_a=1/2×S_e×(1+R)^1/2,其中S_a代表摆动强度,S_e代表材料的疲劳强度,R代表应力的比值(最小应力/最大应力)。