实验一高斯光束和发散角的测量

实验报告一、实验题目：激光束光学特性的实验测量 二、实验内容及部分原理：测量激光束质量因子M2、光束束腰大小w0、位置z0和光束远场发散角 高斯光束在自由空间的传播满足方程（1）()1202202=-Zz wz w（1）方程（1）中， λπ2020w Z=称为瑞利尺寸或共焦参数。

沿光轴方向，任一位置z 处的光斑半径可由公式（2）描述()()2020202z z ww z w -⎪⎪⎭⎫⎝⎛+=πλ （2）其中，w 0是光束的束腰半径，λ 为光波长，z 0 是束腰的位置。

激光束质量因子M 2作为评价参量， 其定义为远场发散角理想高斯光束腰束宽度远场发散角实际光束束腰宽度⨯⨯=2M（3）具体表示为 λθπ02W M=（4）其中，W 0是实际光束的束腰半径，θ 是其远场发散角。

因此，对于实际激光束，其光斑方程可以写为 ()()20204202z z WM W z W-⎪⎪⎭⎫⎝⎛+=πλ （5）公式（4）和（5）可以取x 和y 方向分量表达形式。

λθπλθπyy yxx xW MW M002002,==（6）()()20204202x x x xx z z WM W z W -⎪⎪⎭⎫⎝⎛+=πλ （7）()()20204202yy y yy z z WM W z W -⎪⎪⎭⎫⎝⎛+=πλ （8）因此，依据公式（4）或（6），M 2的测量归结为光束束腰半径W 0和远场发散角θ 的测量确定。

为了在测量中确定光束的有效宽度W ，目前多采用光功率分布的二阶矩测量法。

()()()()z z W z z W yy xx σσ2,2== （9）其中，()()z z y xσσ和称为光功率函数的二阶矩，定义为()()()()⎰⎰⎰⎰⋅-=dxdyy x I dxdyy x I x x z g x,,22σ（10）()()()()⎰⎰⎰⎰⋅-=dxdy y x I dxdyy x I y y z gy,,22σ（11）由于实际测量是逐点进行的，因此，公式（10）和（11）可变换为离散形式()()()[]()∑∑⋅-=ii i ii i gixy x I y x I x xz ,,22σ（12）()()()[]()∑∑⋅-=jj jjj j gjyy xI y x I y yz ,,22σ（13）其中，y g 是光束横截面的重心。

光信息专业实验报告：氦氖激光模式实验氦氖激光器在实际应用，尤其是基础实验教育中应用非常广泛。

本实验对氦氖激光器的性质进行了测量，主要分为两个部分。

一是氦氖激光器光斑大小和发散角的测量，二是利用共焦球面扫描干涉仪与示波器对氦氖激光器的模式进行分析。

实验仪器及技术参数：1、氦氖激光器：中心波长632.8nm、谐振腔腔长246mm、谐振腔曲率半径为1m2、共焦球面扫描干涉仪：腔长20mm、凹面反射镜曲率半径20mm、凹面反射镜反射率99%、精细常数>100、自由光谱范围4GHz3、示波器、光学镜若干实验一氦氖激光器光斑大小和发散角的测量氦氖激光器发出的光束为高斯光束，高斯光束是我们非常熟悉的一种光束。

我们可以从横向和纵向两个角度来理解高斯光束。

1、横向方向高斯光束之所以称为高斯光束，正是因为其基模在横向上光强的分而呈高斯分布型。

即⁄]（1）是I oo(r,z)=I oo(z)exp[−2r2w2(z)其中，下标00表示基横模，I oo(z)表示中心处的光强，r表示横截面离中心的距离，z 表示所研究的光斑所处的纵向上的位置，w(z)表示z处的光束半径。

光束半径w(z)定义为振幅下降到中心振幅1/e的点离中心的距离，或者说光强下降到中心光强1/e2的点离中心的距离。

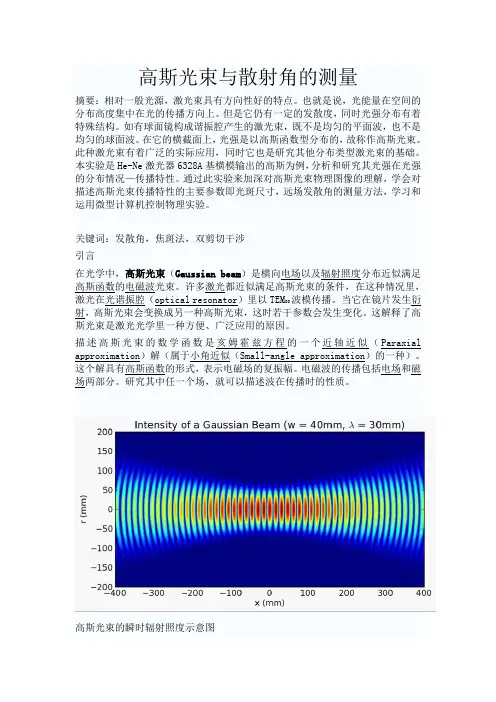
从（1）式可以看出，高斯光束横向上光强随着离中心位置越远，光强越小，至w(z)处已基本下降为0，集中了86.5%的功率。

以上的说明可以用图1表示。

图1 高斯光束横向上振幅分布和光强分布2、纵向方向由横向方向上高斯光束的说明可以看出，整个高斯光束可以看成是横向上高斯光斑沿纵向z 轴传播形成的。

那么，纵向上光斑是如何传播的呢？理想的高斯光事假设传播过程中光的总能量不变，传播的过程只是光斑大小发生了变化。

激光器发出的激光束在空间的传播如图2所示。

光束截面最细处成为束腰。

我们将柱坐标（z, r, φ）的原点选在束腰截面的中点，z是光束传播方向。

束腰截面半径为w0,距束腰为z处的光斑半径为w(z)，则w(z)=w o[1+(λzπw o)2]12⁄（2）其中是λ激光波长。

实验十三 氦氖激光束光斑大小和发散角测量一、激光原理概述1．普通光源的发光——受激吸收和自发辐射普通常见光源的发光（如电灯、火焰、太阳等的发光）是由于物质在受到外来能量（如光能、电能、热能等）作用时，原子中的电子就会吸收外来能量而从低能级跃迁到高能级，即原子被激发。

激发的过程是一个“受激吸收”过程。

处在高能级（E2）的电子寿命很短（一般为10－8～10－9秒），在没有外界作用时会自发地向低能级（E1）跃迁，跃迁时将产生光（电磁波）辐射。

辐射光子能量为12E E h −=ν这种辐射称为自发辐射。

原子的自发辐射过程完全是一种随机过程，各发光原子的发光过程各自独立，互不关联，即所辐射的光在发射方向上是无规则的射向四面八方，另外位相、偏振状态也各不相同。

由于激发能级有一个宽度，所以发射光的频率也不是单一的，而有一个范围。

在通常热平衡条件下，处于高能级E 2上的原子数密度N 2，远比处于低能级的原子数密度低，这是因为处于能级E 的原子数密度N 的大小随能级E 的增加而指数减小，即N∝exp(-E/kT)，这是著名的波耳兹曼分布规律。

于是在上、下两个能级上的原子数密度比为]/)(exp[/1212kT E E N N −−∝式中k 为波耳兹曼常量，T 为绝对温度。

因为E 2>E 1，所以N 2<N 1。

例如，已知氢原子基态能量为E 1＝－13.6eV，第一激发态能量为E 2=-3.4eV，在20℃时，kT≈0.025eV，则0)400exp(/12≈−∝N N可见，在20℃时，全部氢原子几乎都处于基态，要使原子发光，必须外界提供能量使原子到达激发态，所以普通广义的发光是包含了受激吸收和自发辐射两个过程。

一般说来，这种光源所辐射光的能量是不强的，加上向四面八方发射，更使能量分散了。

2.受激辐射和光的放大由量子理论知识了解，一个能级对应电子的一个能量状态。

电子能量由主量子数n(n=1,2,…)决定。

实验二高斯光束的测量一 实验目的1.熟悉基模光束特性。

2.掌握高斯光速强度分布的测量方法。

3.测量高斯光速的远场发散角。

二 实验原理众所周知，电磁场运动的普遍规律可用Maxwell 方程组来描述。

对于稳态传输光频电磁场可以归结为对光现象起主要作用的电矢量所满足的波动方程。

在标量场近似条件下，可以简化为赫姆霍兹方程，高斯光束是赫姆霍兹方程在缓变振幅近似下的一个特解，它可以足够好地描述激光光束的性质。

使用高斯光束的复参数表示和ABCD 定律能够统一而简洁的处理高斯光束在腔内、外的传输变换问题。

在缓变振幅近似下求解赫姆霍兹方程，可以得到高斯光束的一般表达式：2r 2i [kr ]A r , zA0 0e2 ( z )e2 R ( z )（ 6）( z)式中， A 0 为振幅常数；0 定义为场振幅减小到最大值的1 e 的 r 值，称为腰斑， 它是高斯光束光斑半径的最小值；( z) 、 R ( z) 、分别表示了高斯光束的光斑半径、等相面曲率半径、相位因子，是描述高斯光束的三个重要参数，其具体表达式分别为：2( z)0 1z （ 7）Z 0z Z 0 （ 8）R( z) Z 0zZ 01z （ 9）tgZ 02其中，Z 0，称为瑞利长度或共焦参数（也有用f 表示）。

（A ）、 高斯光束在 z const 的面内，场振幅以高斯函数e r 22 ( z )的形式从中心向外平滑的减小，因而光斑半径( z) 随坐标 z 按双曲线：2( z)z （ 10）2 1Z 0规律而向外扩展，如图四所示高斯光束以及相关参数的定义图四（B ）、 在（ 10）式中令相位部分等于常数，并略去( z ) 项，可以得到高斯光束的等相面方程：r 2 const（ 11）z2 R( z)因而，可以认为高斯光束的等相面为球面。

（C ）、瑞利长度的物理意义为：当z Z 0 时， (Z 0)2 0 。

在实际应用中通常取 zZ 0 范围为高斯光束的准直范围，即在这段长度范围内，高斯光束近似认为是平行的。

第1篇一、实验目的1. 加深对高斯光束物理图像的理解；2. 学会对描述高斯光束传播特性的主要参数，即光斑尺寸、远场发散角的测量方法进行掌握；3. 学习体会运用微机控制物理实验的方法。

二、实验原理1. 高斯光束的传播特性高斯光束的振幅在传播平面上呈高斯分布，近场时近似为平面波，远场时近似为球面波。

高斯光束的振幅分布公式为：\[ I(r, z) = I_0 \exp\left(-\frac{2r^2}{w_0^2(z)}\right) \]其中，\( I(r, z) \) 为距离光轴距离为 \( r \) 处，距离光束传播方向为 \( z \) 处的光强；\( I_0 \) 为光束中心处的光强；\( w_0 \) 为光束中心处的光斑尺寸。

光斑尺寸 \( w(z) \) 与光束中心处的光斑尺寸 \( w_0 \) 的关系为：\[ w(z) = w_0 \sqrt{1 + \left(\frac{z}{z_r}\right)^2} \]其中，\( z_r \) 为光束的瑞利长度。

2. 发散角的定义及测量光束的全发散角定义为光束中光强下降到中心光强的 \( 1/e \) 位置时，光束边缘与光轴所成的角度。

在远场情况下，光束的全发散角近似为：\[ \theta = \frac{1.22 \lambda}{w(z)} \]其中，\( \lambda \) 为光束的波长。

三、实验仪器与设备1. 激光器：输出波长为 \( \lambda = 632.8 \) nm 的红光激光；2. 凹面镜：曲率半径为 \( R = 50 \) cm；3. 平面镜：用于反射激光；4. 光电探测器：用于测量光强；5. 数据采集卡：用于采集光电探测器数据；6. 计算机：用于处理实验数据。

四、实验步骤1. 将激光器输出光束照射到凹面镜上，使光束经凹面镜反射后形成高斯光束；2. 将光电探测器放置在凹面镜后的某个位置，调整探测器位置，使探测器接收到的光强最大；3. 记录探测器接收到的光强 \( I \)；4. 根据公式 \( I = I_0 \exp\left(-\frac{2r^2}{w_0^2(z)}\right) \) 求解光斑尺寸 \( w_0 \)；5. 根据公式 \( \theta = \frac{1.22 \lambda}{w(z)} \) 求解发散角\( \theta \)；6. 重复步骤 3-5，改变探测器位置，记录不同位置的光强 \( I \) 和发散角\( \theta \)。

2016新编激光光束发散角的测量激光光束发散角的测量一、高斯光束由激光器产生的激光束既不是平面光波，也不是均匀的球面光波。

虽然在特定位置，看似一个球面波，但它的振幅和等相位面都在变化。

从理论上来讲，光在稳定的激光谐振腔中进行无限次的反射后，激光器所发出的激光将以高斯光束的形式在空间传输。

而且反射(衍射)次数越多，其光束传输形状越接近高斯光束。

从另一方面讲，形状越接近高斯光束的激光束，在传播、偶合及光束变换过程中，其形状越不易改变，在高斯光束时，不论怎样变换，其形状依然是高斯光束。

在激光器产生的各种模式的激光中，最基本、应用最多的是基模高斯光束。

在以光束传播方向z轴为对称轴的柱面坐标系中，基模高斯光束的电矢量振动可以表示为22rrz,[()arctan，,ikz2E,,it()2()wzRzf0 (1) (,,),,,Erzteee00()wz式中，E为常数，其余各符号意义表示如下: 0222 rxy,，2,, k,z2 wzw()1(),，0f2fRzz(),， z2,w0,f,其中，wwz,,(0)为基模高斯光束的束腰半径，f称为高斯光束的共焦参数或瑞利长度，0R(z)为与传播轴线交于z点的基模高斯光束的远场发散角为高斯光束等相位面的曲率半径，w(z) 是与传播轴线相交于z点高斯光束等相位面上的光斑半径。

图1 高斯光束的横截面图2 高斯光束的纵剖面，按双曲线的规律扩展基模高斯光束具有以下基本特点:1)基模高斯光束在横截面内的电矢量振幅分布按照高斯函数规律从中心向外平滑下降，如图1所示。

由中心振幅值下降到1/e点所对应的宽度，定义为光斑半径，光斑半径是传播位置z的函数z2 (1) wzw()1(),，0f由(1)式可见，光斑半径随着传播位置坐标z按双曲线的规律展开，即22wzz() (2) ,,122wf0如图2所示，在z=0处，，光斑达到极小值，称为束腰半径。

由(2)式可wzw(),0知，知道束腰半径和瑞利长度，即可确定任何位置处的光斑半径。

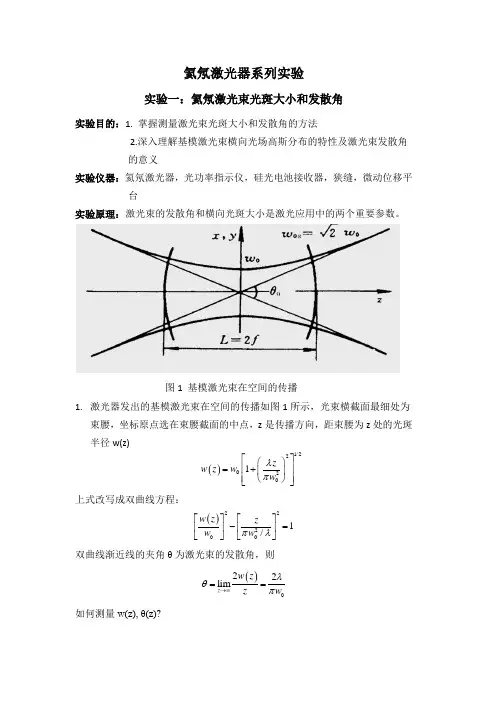
氦氖激光器系列实验实验一：氦氖激光束光斑大小和发散角实验目的：1. 掌握测量激光束光斑大小和发散角的方法2.深入理解基模激光束横向光场高斯分布的特性及激光束发散角的意义实验仪器：氦氖激光器，光功率指示仪，硅光电池接收器，狭缝，微动位移平台实验原理：激光束的发散角和横向光斑大小是激光应用中的两个重要参数。

图1 基模激光束在空间的传播1. 激光器发出的基模激光束在空间的传播如图1所示，光束横截面最细处为束腰，坐标原点选在束腰截面的中点，z 是传播方向，距束腰为z 处的光斑半径w(z)()1/220201z w z w w λπ⎡⎤⎛⎫⎢⎥=+ ⎪⎢⎥⎝⎭⎣⎦上式改写成双曲线方程：()222001/w z z w w πλ⎡⎤⎡⎤-=⎢⎥⎢⎥⎣⎦⎣⎦ 双曲线渐近线的夹角θ为激光束的发散角，则()022lim z w z z w λθπ→∞==如何测量w(z), θ(z)?w(z)： 方法一：测出z ，算出w 0,可知w(z)方法二：根据光斑半径定义测量. θ(z )： 方法一：算出w 0，可求θ(z)方法二：测出离束腰很远的z 和光斑大小w(z)，算出θ(z) 本实验要求分别用两种方法计算出结果进行比较。

2. 激光束横向光场分布激光沿z 轴传播，基模高斯光束分布的形式：()()222arctan 200,,()r z r i k z R f w z CE x y z e ew z ⎡⎤⎛⎫-+--⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎣⎦=⋅⋅则基模振幅：()()2200,()r w z CE r z e w z -=⋅光斑半径w(z)定义：振幅下降到1/e 的点离中心的距离。

实际测量中，只能测得光束横向光强分布，光强正比于振幅的平方()()()2222200002,,()r w z CI r z E r z e w z -∝=⋅所以，光束半径w(z)也可定义为中心光强e -2倍的点离中心的距离。

在光束半径w(z)范围内集中了86.5%的总功率。

激光光束发散角的测量一、高斯光束由激光器产生的激光束既不是平面光波，也不是均匀的球面光波。

虽然在特定位置，看似一个球面波，但它的振幅和等相位面都在变化。

从理论上来讲，光在稳定的激光谐振腔中进行无限次的反射后，激光器所发出的激光将以高斯光束的形式在空间传输。

而且反射（衍射）次数越多，其光束传输形状越接近高斯光束。

从另一方面讲，形状越接近高斯光束的激光束，在传播、偶合及光束变换过程中，其形状越不易改变，在高斯光束时，不论怎样变换，其形状依然是高斯光束。

在激光器产生的各种模式的激光中，最基本、应用最多的是基模高斯光束。

在以光束传播方向z 轴为对称轴的柱面坐标系中，基模高斯光束的电矢量振动可以表示为222[()arctan ()2()000(,,)()r r z i k z i t w z R z f E E r z t e e e w z ω-+--=⋅⋅ （1）式中，E 0为常数，其余各符号意义表示如下：222r x y =+2k πλ=()w z w =2()f R z z z=+ 20w f πλ= 其中，0(0)w w z ==为基模高斯光束的束腰半径，f 称为高斯光束的共焦参数或瑞利长度，R (z )为与传播轴线交于z 点的基模高斯光束的远场发散角为高斯光束等相位面的曲率半径，w (z ) 是与传播轴线相交于z 点高斯光束等相位面上的光斑半径。

图1 高斯光束的横截面图2 高斯光束的纵剖面，按双曲线的规律扩展基模高斯光束具有以下基本特点：1）基模高斯光束在横截面内的电矢量振幅分布按照高斯函数规律从中心向外平滑下降，如图1所示。

由中心振幅值下降到1/e 点所对应的宽度，定义为光斑半径，光斑半径是传播位置z 的函数()w z w =（1） 由（1）式可见，光斑半径随着传播位置坐标z 按双曲线的规律展开，即22220()1w z z w f-= （2） 如图2所示，在z =0处，0()w z w =，光斑达到极小值，称为束腰半径。

实验十三 氦氖激光束光斑大小和发散角测量一、激光原理概述1．普通光源的发光——受激吸收和自发辐射普通常见光源的发光（如电灯、火焰、太阳等的发光）是由于物质在受到外来能量（如光能、电能、热能等）作用时，原子中的电子就会吸收外来能量而从低能级跃迁到高能级，即原子被激发。

激发的过程是一个“受激吸收”过程。

处在高能级（E2）的电子寿命很短（一般为10－8～10－9秒），在没有外界作用时会自发地向低能级（E1）跃迁，跃迁时将产生光（电磁波）辐射。

辐射光子能量为12E E h −=ν这种辐射称为自发辐射。

原子的自发辐射过程完全是一种随机过程，各发光原子的发光过程各自独立，互不关联，即所辐射的光在发射方向上是无规则的射向四面八方，另外位相、偏振状态也各不相同。

由于激发能级有一个宽度，所以发射光的频率也不是单一的，而有一个范围。

在通常热平衡条件下，处于高能级E 2上的原子数密度N 2，远比处于低能级的原子数密度低，这是因为处于能级E 的原子数密度N 的大小随能级E 的增加而指数减小，即N∝exp(-E/kT)，这是著名的波耳兹曼分布规律。

于是在上、下两个能级上的原子数密度比为]/)(exp[/1212kT E E N N −−∝式中k 为波耳兹曼常量，T 为绝对温度。

因为E 2>E 1，所以N 2<N 1。

例如，已知氢原子基态能量为E 1＝－13.6eV，第一激发态能量为E 2=-3.4eV，在20℃时，kT≈0.025eV，则0)400exp(/12≈−∝N N可见，在20℃时，全部氢原子几乎都处于基态，要使原子发光，必须外界提供能量使原子到达激发态，所以普通广义的发光是包含了受激吸收和自发辐射两个过程。

一般说来，这种光源所辐射光的能量是不强的，加上向四面八方发射，更使能量分散了。

2.受激辐射和光的放大由量子理论知识了解，一个能级对应电子的一个能量状态。

电子能量由主量子数n(n=1,2,…)决定。