e8He-Ne激光器光束强度分布及其发散角的测量

2017年35期Technology Innovation and Application 方法创新氦氖激光束光斑半径及发散角测量方法的改进何颖卓，李春芝，杜新迪(内蒙古民族大学物理与电子信息学院，内蒙古通辽028043)摘要：随着激光在我们现代生活中越来越多地应用，需要更深入地研究激光物理参量。

氦氖激光束光斑半径及发散角是激光器的两个 重要物理参量。

通过对两个参量测量实验的研究，对常规测量方法进行改进，得到一个更简便测量光斑半径的方法。

并对两种测量方法分别进 行了几个不同位置光斑半径的测量，对测量数据进行比对分析研究，得出改进后的测量方法具有简单及精确度较高等优点…此外，对测量位置 选择范围进行了一些讨论这些研究内容有助于人们加深对激光器的了解和认识，为更好的应用激光提供一些科学依据.关键词：激光;光斑半径；发散角中图分类号:TN 241文献标志码：A文章编号：2095-2945(2017)35-0089-02激光以其亮度高、相干性好、单色性和方向性好等特征在现代科技及日常生产生活中已有较多的应用，为了更广泛地 应用激光，我们对氦氖激光束光斑半径及发散角等重要物理 参量进行了更深人地研究M 。

通常测量氦氖激光束光斑半径 的方法是:先根据激光器光束选择一个测量位置，并进行相对 于激光束横向位置和对应光强的测量，利用这些数据作图就 可以得到激光束光斑半径，再通过计算还能得到激光束发散 角的大小P 1。

这种测量方法存在两个问题:一是测量位置的选 择问题;二是该测量方法常规测量的数据多比较繁琐的问题. 我们通过大量的实验研究对通常测量方法进行改进，得到一 个简单的测量光斑半径的方法，并得到更好的实验效果。

通过 这些研究可以完善氦氖激光束光斑半径的测量，为从事激光 器应用与研究人士提供参考。

1实验原理1.1氦氖激光束的光斑半径及发散角[3]氦氖激光器发出的激光在垂直于激光束传播方向截面上 的光强分布为：I (r.z) = I (z)e x p —-(1)U J -(Z )上式光强振幅分布是高斯分布，这样的激光束被称为高斯光束叱光束截面最细处称为束腰其半径为C 0。

刀口法测量He-Ne激光束发散角实验的再认识魏奶萍;张相武【摘要】The method of edge of He-Ne laser beam divergence angle measurement principle is proved in theo-ry,and then according to the relative power of 0. 25 and 0. 75 points in laser Gaussian distribution curve on both sides of the maximum. The data measured in the experiment are processed by curve fitting,the laser beam divergence angle is obtained.%对刀口法测量He-Ne激光束发散角的测量原理从理论上进行了证明，然后根据激光束相对功率为0.25和0.75的点位于高斯分布曲线极大值两侧，距离为ep=0.6745σ=0.3373W ，对测量实验数据进行曲线拟合，求得其激光光束发散角。

【期刊名称】《大学物理实验》【年(卷),期】2015(000)004【总页数】3页(P78-80)【关键词】刀口法;曲线拟合;发散角【作者】魏奶萍;张相武【作者单位】西安文理学院，陕西西安 710065;西安文理学院，陕西西安 710065【正文语种】中文【中图分类】TN206在激光应用中，激光光束的发散角是一个很重要的参数，它的测量精度会直接影响到光束质量因子M2［1-4］．目前，常用的测量方法有焦点刀口扫描法［5］、CCD 摄像法［6］、偏振光干涉法［7］和BBO晶体倍频法［8］等．但在大学本科期间，对He-Ne激光束发散角的测量仍然采用的是刀口法［9］，学生对于刀口法测量原理中的相关内容不甚清楚(激光束发散角在其相对功率为0．25和0．75的点位于高斯分布曲线极大值的两侧，其距离为ep=0．674 5σ =0．337 3W ．)．鉴于此，对刀口法测量原理想从理论上予以证明，然后再结合实验数据进行曲线拟合，求得其激光光束发散角。

He-Ne激光的纵模及基模的远场发散角一、实验目的：1、通过测试分析，掌握模式分析的基本方法。

2、对实验中使用的重要分光仪器——共焦球面扫描干涉仪，了解其原理、性能，学会正确使用。

3、熟悉谐振腔的构成，学会调整的方法，体会谐振腔调整之后一些激光参数的变化。

二、实验内容：1、He-Ne激光器模式分析要测量和分析出激光器所具有的纵模个数，纵模频率间隔值，横模个数，横模频率间隔值，不同位置基模对应的光斑图形1）通过共焦球面干涉仪接示波器观察纵模频率间隔，再根据自由光谱范围的定义，确定它所对应的频率间隔（即哪两条谱线间距为ΔvS.R. ）为减少测量误差，需要对x轴增幅，测出与ΔvS.R.相对应的标尺长度，计算出两者比值，即每厘米代表的频率间隔值。

（2）通过减小光阑大小，观察模式变化。

1、He-Ne激光器模式分析（1）点燃外腔激光器。

（2）调整光路，首先使激光束从光阑小孔通过，调整扫描干涉仪上下、左右位置，使光束正入射孔中心，再细调干涉仪板架上的两个方位螺丝，使从干涉仪腔镜反射的最亮的光点回到光阑小孔的中心附近，这时表明入射光束和扫描干涉仪的光轴基本重合。

（3）将放大器的接收部位对准扫描干涉仪的输出端。

接通放大器、锯齿波发生器、示波器的开关，观察示波器上的展现的频谱图，进一步细调干涉仪的两个方位螺丝，使谱线尽量强，噪声最小。

（4）改变锯齿波输出电压的峰值，看示波器上干涉序的数目有何变化，确定示波器上应展示的干涉序个数。

根据干涉序个数和频谱的周期性，确定哪些模属于同一k序。

（5）根据自由光谱范围的定义，确定它所对应的频率间隔（即哪两条谱线间距为ΔvS.R. ）为减少测量误差，需要对x轴增幅，测出与ΔvS.R.相对应的标尺长度，计算出两者比值，即每厘米代表的频率间隔值。

（6）在同一干涉序k内观测，根据纵模定义对照频谱特征，确定纵模的个数，并测出纵模频率间隔ΔvΔq＝1。

与理论值比较，检查辨认和测量的值是否正确。

He-Ne激光器偏振光数据处理与分析1、He-Ne激光器偏振光测量表1 He-Ne激光器偏振光测量数据表偏振角度(°)输出功率（mW）偏振角度(°)输出功率（mW）偏振角度(°)输出功率（mW）0 1.1361250.8032500.0905 1.0731300.8592550.096100.9951350.9342600.119150.835140 1.0022650.169200.743145 1.0662700.204250.665150 1.1172750.252300.556155 1.1452800.315350.464160 1.1872850.412400.378165 1.2012900.495450.291170 1.1722950.618500.225175 1.1473000.710550.170180 1.1043050.801600.130185 1.0343100.867650.0981900.9483150.966700.0881950.841320 1.027750.0922000.755325 1.102800.1132050.659330 1.145850.1532100.574335 1.174900.1982150.473340 1.192950.2812200.386345 1.1831000.3622250.285350 1.1681050.4592300.223355 1.1471100.5252350.172360 1.0981150.6082400.1271200.6992450.099图1 He-Ne激光器偏振特性曲线图分析：由图1 He-Ne 激光器偏振特性曲线图可知，He-Ne 激光器输出的光为线偏振光；而且从图中曲线可知，曲线并非完全的平滑，有一定的凹凸瑕疵，这说明实验存在误差，这主要是受实验环境光变化的影响所致。

He-Ne激光器高斯光束腰斑测量实验He-Ne激光器高斯光束腰斑测量一、实验目的1、加深对高斯光束物理图像的理解；2、加强对高斯光束传播特性的了解；3、掌握用CCD法和刀口法测量高斯光束光斑大小；4、了解并掌握远场发散角的定量测量方法；二、实验设备He-Ne激光器、激光电源、光功率计、滤光片、衰减片、CCD相机、光学光具座、示波器、数据采集卡、计算机等。

三、实验原理（一）CCD测量法实验系统结构如右图所示：实验中，将光具座导轨上的CCD相机沿着激光传播方向均匀移动，实时地记录CCD相机在光具座标尺上的不同位置以及对应的纵向平面上的光斑尺寸。

光斑半径ω(z)---定义为在光束传播方向上z处的横截面内圆形光斑半径，可表示为（1）利用公式（1）可得（2）对于两个不同的位置，有（3）即：（4）以（若对精度有更高要求，可适当增加小数位数）为判据，选择适当步长逐步减小测量所得的最小光斑半径，将每次减小后的光斑半径值与测量所得任意两个刻度处的光斑半径叠带入式（4），运用光腰判据进行光腰半径的求解；同时利用可求解出远场发散角。

（二）刀口测量法1、实验装置如图所示2、实验原理：相比于CCD法，刀口法适用于高功率激光的质量分析。

在理论上是根据光腰的定义（强度的）即能量下降到中心光斑能量的86.5%来测量。

但是由于刀口方向（Y轴向）的积分范围的扩大，光束腰的界定一般以能量下降到95.4%为准。

所以在高斯激光束束腰处横截面内的强度分布可表示为：（5）式中为激光的总功率，为按照强度所定义的腰斑半径。

对于高斯光束，场并不是局域于的范围内，如上图所示，在Y方向上应延伸到无穷远，只是在的区域内光强很弱。

以为半径的范围内的光强占总光强的百分比为：所以以为半径的范围内的光强能量占总光强能量的86.466%。

如果按照刀口测量时的实际范围，则由此可见，实际测量时测出的光强与总光强能量的比值为95.44%，比原来的比值要大得多。

四、实验内容（1）用刀口法确定高斯光束束腰在不同位置所对应的光斑半径并计算远场发散角（2）用CCD法观察高斯光束图样五、实验步骤（一）刀口测量法1.在刀口未切割光束情况下，调整激光在光具座上的方向及位置；2.将光束对准功率计；并调整，根据功率计的读数最大值来确定光功率计处于最佳接收状态；3.在激光和光功率计之间放一个微型小孔（针孔挡片），让挡片在光束传播方向来回移动，通过光功率计的读数，找到最大值处，即该处为光束束腰位置（测量时，该处也是刀口位置），并固定好光功率计；4.取走挡片，记录功率计的最大读数，此为激光光束的总功率；5.用刀口代替挡片，旋动刀口测微螺母，让刀口切割光束，直至光功率计的读数为，记录该处测微螺母的读数；再继续选装测微螺母至处，并记录该处读数为，得出（高斯激光束束腰在该处的直径）.6.移动刀口位置，并记下不同位置所对应的束腰直径ΔX待数据记录好后整理实验仪器并惊醒数据的分析与处理。

实验一：He-Ne 激光器谐振腔调整和激光特性的测量一、实验目的：1.了解He-Ne 激光器的构造。

2. 观察并测量He-Ne 激光器的功率、发散角等特性参数。

3. 调整谐振腔一端的反射镜，观察谐振腔改变后He-Ne 激光器性能参数的变化。

4. 了解外腔He-Ne 激光器的偏振态。

5. 通过光栅方程来验证He-Ne 激光的波长。

二、实验内容：1. He-Ne 激光器发散角测量由于远场发散角实际是以光斑尺寸为轨迹的两条双曲线的渐近线间的夹角，所以我们应延长光路以保证其精确度，此时需要在前方放置反射镜。

可以证明当距离大于λωπ207时所测的全发散角与理论上的远场发散角相比误差仅在1%以内。

（1）确定和调整激光束的出射方向，放置一个反射镜来延长光路。

（2）在光源前方L1处用光功率计检测，在与光轴垂直的某方向延正负轴测量并绘出光功率/位移曲线。

（3）由于光功率/位移曲线是高斯分布的，定义Pmax/e2为光斑边界，测量出L1位置的光斑直径D1。

（4）在后方L2处用光功率计同样测绘光强/位移曲线，并算出光斑直径D2。

（5）由于发散角度较小，可做近似计算，θ2=D2-D1/L2-L1,便可以算出全发散角2θ。

2 .利用光栅方程验证波长。

He-Ne 激光器的波长是623.8nm, 通过光栅方程可以验证激光器的波长值。

观察衍射图样，统计出衍射级数j 。

根据三角公式，计算出衍射角θ。

由于光栅常数d 已知，根据光栅方程可以计算出激光波长。

),2,1,0(sin ±±==j j d λθ1. 观察He-Ne 外腔激光器模型，了解各部分构造及工作原理。

He-Ne 激光器的组成包括有：共振腔（由放电毛细管和反射镜组成）、工作物质（有氦氖气体按一定比例组成）、放电电源（通常多采用直流高压电源）。

当氦氖激光器的电极上加上几千伏的直流高压后，管内就产生辉光发电，对工作物质进行激励从而引起受激辐射，经共振腔进行光放大以后，即产生激光输出。

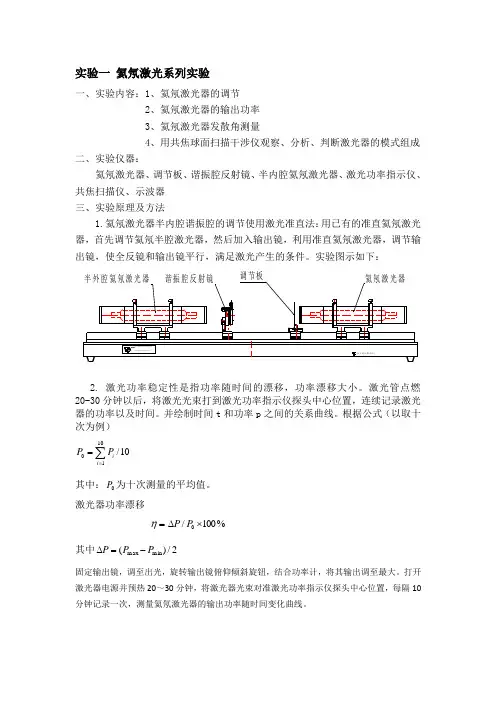
实验一 氦氖激光系列实验一、实验内容：1、氦氖激光器的调节 2、氦氖激光器的输出功率 3、氦氖激光器发散角测量4、用共焦球面扫描干涉仪观察、分析、判断激光器的模式组成 二、实验仪器：氦氖激光器、调节板、谐振腔反射镜、半内腔氦氖激光器、激光功率指示仪、共焦扫描仪、示波器 三、实验原理及方法次为例）10/1010∑==i i P P其中：0P 为十次测量的平均值。

激光器功率漂移=η%100/0⨯∆P P 其中2/)(min max P P P -=∆固定输出镜，调至出光，旋转输出镜俯仰倾斜旋钮，结合功率计，将其输出调至最大。

打开激光器电源并预热20～30分钟，将激光器光束对准激光功率指示仪探头中心位置，每隔10分钟记录一次，测量氦氖激光器的输出功率随时间变化曲线。

3. 用刀口法可以测定光斑的大小和验证光斑的光强分布是高斯分布。

实验中使刀口平行于y 轴，沿垂直于x 轴方向移动当刀口缓慢推入光束时，设刀口挡住了a x ≤的所有点。

未被刀口挡住而通过的光功率P 用余误差函数表示为：)2(2),(0a Werfc P dxdy y x I P a==⎰⎰ 如果先用刀口把光束全部挡住，然后把刀口缓慢拉出时，未被刀口挡住而通过的光功率可用相应的误差函数表示。

)exp(),(2220σy x p y x I +-=)2(210σaerfc p p = 其中2/W =σ是数理统计中的标准偏差。

根据上式作出的归一化高斯分布和相对功率与刀口位置关系曲线如下图所示可以证明，相对功率为0.25和0.75的点分别位于高斯分布曲线极大值两侧，其距离σ6745.0=p e 。

所以从由实验得到的相对功率与刀口位置的关系曲线就可确定p e 的值。

算出σ值后就可计算P/0P 的理论值，进行曲线拟合。

如果拟合的好，就证明基横模光强是高斯分布。

用p e 的值可以计算光斑大小：)2(4826.1p e W = )2(7456.12/1p e D =如图所示，将刀口位于激光光斑边缘位置，并将功率计置于刀口后面来测量未被刀口挡住的激光光功率。

激光光束发散角的测量一、高斯光束由激光器产生的激光束既不是平面光波，也不是均匀的球面光波。

虽然在特定位置，看似一个球面波，但它的振幅和等相位面都在变化。

从理论上来讲，光在稳定的激光谐振腔中进行无限次的反射后，激光器所发出的激光将以高斯光束的形式在空间传输。

而且反射（衍射）次数越多，其光束传输形状越接近高斯光束。

从另一方面讲，形状越接近高斯光束的激光束，在传播、偶合及光束变换过程中，其形状越不易改变，在高斯光束时，不论怎样变换，其形状依然是高斯光束。

在激光器产生的各种模式的激光中，最基本、应用最多的是基模高斯光束。

在以光束传播方向z 轴为对称轴的柱面坐标系中，基模高斯光束的电矢量振动可以表示为222[()arctan ()2()000(,,)()r r z i k z i t w z R z f E E r z t e e e w z ω-+--=⋅⋅ （1）式中，E 0为常数，其余各符号意义表示如下：222r x y =+2k πλ=()w z w = 2()f R z z z=+ 20w f πλ= 其中，0(0)w w z ==为基模高斯光束的束腰半径，f 称为高斯光束的共焦参数或瑞利长度，R (z )为与传播轴线交于z 点的基模高斯光束的远场发散角为高斯光束等相位面的曲率半径，w (z ) 是与传播轴线相交于z 点高斯光束等相位面上的光斑半径。

图1 高斯光束的横截面图2 高斯光束的纵剖面，按双曲线的规律扩展基模高斯光束具有以下基本特点：1）基模高斯光束在横截面内的电矢量振幅分布按照高斯函数规律从中心向外平滑下降，如图1所示。

由中心振幅值下降到1/e 点所对应的宽度，定义为光斑半径，光斑半径是传播位置z 的函数()w z w = （1） 由（1）式可见，光斑半径随着传播位置坐标z 按双曲线的规律展开，即22220()1w z z w f -= （2）如图2所示，在z =0处，0()w z w =，光斑达到极小值，称为束腰半径。

2016新编激光光束发散角的测量激光光束发散角的测量一、高斯光束由激光器产生的激光束既不是平面光波，也不是均匀的球面光波。

虽然在特定位置，看似一个球面波，但它的振幅和等相位面都在变化。

从理论上来讲，光在稳定的激光谐振腔中进行无限次的反射后，激光器所发出的激光将以高斯光束的形式在空间传输。

而且反射(衍射)次数越多，其光束传输形状越接近高斯光束。

从另一方面讲，形状越接近高斯光束的激光束，在传播、偶合及光束变换过程中，其形状越不易改变，在高斯光束时，不论怎样变换，其形状依然是高斯光束。

在激光器产生的各种模式的激光中，最基本、应用最多的是基模高斯光束。

在以光束传播方向z轴为对称轴的柱面坐标系中，基模高斯光束的电矢量振动可以表示为22rrz,[()arctan，,ikz2E,,it()2()wzRzf0 (1) (,,),,,Erzteee00()wz式中，E为常数，其余各符号意义表示如下: 0222 rxy,，2,, k,z2 wzw()1(),，0f2fRzz(),， z2,w0,f,其中，wwz,,(0)为基模高斯光束的束腰半径，f称为高斯光束的共焦参数或瑞利长度，0R(z)为与传播轴线交于z点的基模高斯光束的远场发散角为高斯光束等相位面的曲率半径，w(z) 是与传播轴线相交于z点高斯光束等相位面上的光斑半径。

图1 高斯光束的横截面图2 高斯光束的纵剖面，按双曲线的规律扩展基模高斯光束具有以下基本特点:1)基模高斯光束在横截面内的电矢量振幅分布按照高斯函数规律从中心向外平滑下降，如图1所示。

由中心振幅值下降到1/e点所对应的宽度，定义为光斑半径，光斑半径是传播位置z的函数z2 (1) wzw()1(),，0f由(1)式可见，光斑半径随着传播位置坐标z按双曲线的规律展开，即22wzz() (2) ,,122wf0如图2所示，在z=0处，，光斑达到极小值，称为束腰半径。

由(2)式可wzw(),0知，知道束腰半径和瑞利长度，即可确定任何位置处的光斑半径。

半外腔He-Ne 激光器的调试及参数测量1. 引言虽然在1917年爱因斯坦就预言了受激辐射的存在，但在一般热平衡情况下，物质的受激辐射总是被受激吸收所掩盖，未能在实验中观察到。

直到1960年，第一台红宝石激光器才面世，它标志了激光技术的诞生按工作物质的类型不同，激光器可以分成四大类：固体激光器、气体激光器、液体激光器和半导体激光器。

He-Ne 激光器是继红宝石激光器后出现的第二种激光器，也是目前使用最为广泛的激光器之一。

因此有必要通过实验对He-Ne 激光器作全面的了解。

2. 实验目的1） 了解He-Ne 激光器的构造。

2） 观察并测量He-Ne 激光器的功率、发散角、横模式等性能参数。

3） 调整谐振腔一端的反射镜，观察谐振腔改变后He-Ne 激光器性能参数的变化。

3. 基本原理3.1 He-Ne 激光器结构He-Ne 激光器由光学谐振腔（输出镜与全反镜）、工作物质（密封在玻璃管里的氦气、氖气）、激励系统（激光电源）构成，如下图He-Ne 激光器激励系统采用开关电路的直流电源，体积小，重量轻，可靠性高，装有散热风机的He-Ne 激光器可长时间运行。

激光管的布儒斯特窗与输出镜、全反镜之间用模具成型的耐老化的硅胶套封接。

避免了因灰尘、潮气污染布氏窗、输出镜、全反镜而造成的激光输出功率下降。

输出镜、全反射调节采用差动螺丝，粗调调节范围大，可锁定。

细调调节范围小，调节时不易出差错。

在激光管的阴极、阳极上串接着镇流电阻,防止激光管在放电时出现闪烁现象。

激光器外壳接地，手碰激光器外壳无静电感应的刺痛感。

放电毛细管内充的氦氖混合气体的压强比约为7:1，总压强在100Pa 至400Pa 。

放电管一端贴有用水晶片制成的布儒斯特窗。

窗口平面的法线与放电管轴向间的夹角也恰好等于水晶的布儒斯特角，约56°。

安装布儒斯特窗口可以使激光器输出的激光为在纸面内振动的偏振光，沿该方向振动的偏振光通过布儒斯特窗时不会反射，因此有利于减少损耗，提高输出功率。

激光原理实验指导书激光原理实验指导书中北⼤学信息与通信⼯程学院实验⼀：He-Ne激光器谐振腔调整和激光特性的测量（2学时）⼀、实验⽬的：1．了解He-Ne激光器的构造。

2. 观察并测量He-Ne激光器的功率、发散⾓等特性参数。

3. 调整谐振腔⼀端的反射镜，观察谐振腔改变后He-Ne激光器性能参数的变化。

4. 了解外腔He-Ne激光器的偏振态5. 通过光栅⽅程来验证He-Ne激光的波长⼆、实验内容：1. He-Ne激光器发散⾓测量关键是如何保证接收器能在垂直光束的传播⽅向上扫描，这是测量光斑尺⼨和发散⾓的必要条件。

由于远场发散⾓实际是以光斑尺⼨为轨迹的两条双曲线的渐近线间的夹⾓，所以我们应延长光路以保证其精确度，此时需要在前⽅放置反射镜。

可以证明当距离⼤于λπ2ω7时所测的全发散⾓与理论上的远场发散⾓相⽐误差仅在1%以内。

（1）确定和调整激光束的出射⽅向，放置⼀个反射镜来延长光路。

（2）在光源前⽅L1处⽤光功率计检测，在与光轴垂直的某⽅向延正负轴测量并绘出光功率/位移曲线。

（3）由于光功率/位移曲线是⾼斯分布的，定义P max/e2为光斑边界，测量出L1位置的光斑直径D1。

（4）在后⽅L2处⽤光功率计同样测绘光强/位移曲线，并算出光斑直径D2。

（5）由于发散⾓度较⼩，可做近似计算，θ2=D2-D1/L2-L1,便可以算出全发散⾓2θ。

2. 外腔He-Ne激光器偏振态验证在外腔He-Ne激光器的谐振腔内由于放置了步儒斯特窗，限制了输出光⽚振态为垂直桌⾯的线偏振，因此，可在输出前⽅放置⼀个偏振⽚，通过旋转偏振⽚来分析外腔He-Ne 激光器激光的偏振⽅向。

3 .利⽤光栅⽅程验证波长。

我们所⽤的He-Ne激光器的波长是623.8nm, 通过光栅⽅程可以验证激光器的波长值。

（1）观察衍射图样，统计出衍射级数j。

（2）见图⼀，根据三⾓公式，计算出衍射⾓θ。

（3）由于光栅常数d已知，根据光栅⽅程可以计算出激光波长。

He-Ne激光器谐振腔调整走进He-Ne激光器气体激光器的优点：1. 工作物质均匀性好，输出激光光束质量好2. 谱线宽，从远红外到紫外3. 输出功率大，转换效率高（电光转换）4. 结构简单，成本低氦氖激光器的结构：工作物质：He-Ne气体（He为辅助气体），气压比为5：1－7：1谐振腔：一般用平凹腔，平面镜为输出镜，透过率约1％－2％，凹面镜为全反射镜泵浦系统：一般采用放电激励激光管结构：按谐振腔与放电管的放置方式分为内腔式﹑外腔式﹑半内腔式按阴极及贮气室的位置不同分为同轴式﹑旁轴式﹑单细管式He－Ne激光器的特点：典型谱线：632.8nm 1.15μm 3.39μm其他谱线：612nm 594nm 543nm优点：1. 光束质量好Θ＜1mrad2.单色质量好，带宽＜22Hz3.稳定性高功率稳定（＜2％）频率稳定（＜5×10-15）4.在可见光区He-Ne激光器的输出功率：He-Ne激光器属于以非均匀加宽为主但又不能忽略均匀加宽影响的综合加宽线型，按照综合加宽的情况计算其输出功率。

输出功率的稳定性：He-He激光器在工作过程中，输出功率会随时间做周期性的或随即的波动。

造成漂移的原因有：1 放电电流波动造成输出功率的波动；2谐振腔光轴与毛细管轴线相对位置发生变化引起功率波动；3纵模的变化引起输出功率的波动。

在只有少数几个纵模振荡的短腔激光器中，温度的变化或其他原因导致腔长发生了变化，谐振腔的纵模也要发生改变，将造成增益曲线的烧孔面积变化，从而引起输出功率的波动。

解决方法：1.外部控制的办法减小功率漂移；2.根据产生漂移的原因，在器件结构和工艺上采取改进措施；He-He激光器的频率特性：在适当的放电条件下，He-He激光器已经获得了100多条谱线。

其中最主要的是0.6328μm和3.39μm两条。

He-Ne的实验调整相对一般光源，激光具有单色性好的特点，也就是说，它具有非常窄的谱线宽度。

这样窄的谱线，不是受激辐射后自然形成的，而是受激辐射经过谐振腔等多种机制的作用和相互干涉后形成的。

氦氖激光器光束的模式分析在激光器的生产与应用中，我们常常需要先知道激光器的模式状况，如精密测量、全息技术等工作需要基横模输出的激光器，而激光器稳频和激光测距等不仅要基横模而且要求单纵模运行的激光器。

因此，进行模式分析是激光器的一项基本又重要的性能测试。

另一方面，在激光器中利用锁模技术可得到持续时间短到皮秒（ps＝10－12s）量级的强脉冲激光。

极强的超短脉冲光源大大促进了像非线性光学、时间分辨激光光谱学、等离子体物理等学科的发展。

氦氖激光器是常见的一种激光器，它在准直、计量、光全息处理等研究领域中有着广泛的应用，但由于普通的He-Ne激光器在功率较高时（即增益管较长时）会出现多个纵模，对于干涉、计量等一些要求单色性很强的激光研究领域不适用。

本实验分析氦氖激光器的模式并进行简单锁模。

【实验目的】1、了解扫描干涉仪原理，掌握其使用方法。

2、学习观测激光束横摸、纵摸的实验方法。

4学习和掌握激光锁模和声光调制原理。

5 掌握锁模激光器结构特定及调试方法。

6 观察腔长变化及调制深度对输出光脉冲的影响。

【实验原理】1共焦球面扫描干涉仪工作原理共焦球面扫描干涉仪（简写FPS ）由两个曲率半径r 相等、镀有高反膜层的球面镜M1、M2组成，两者之间的距离L 称作腔长，如图1所示。

压电陶瓷内外两面加上锯齿波电压后，驱动一个反射镜作周期性运动，用以改变腔长L 而实现光谱扫描。

由于腔长L 恰等于曲率半径r ，所以两反射镜焦点重合，组成共焦系统。

当一束波长为λ的光近轴入射到干涉仪内时，在忽略球差情况下，光线走一闭合路径，即光线在腔内反射，往返两次之后又按原路行进。

图1 共焦球面扫描干涉仪结构示意图从图1可以看出，一束入射光将有1、2两组透射光。

若m 是光线在腔内往返的次数，则1组经历了4m 次反射；2组经历了4m+2次反射。

设反射镜的反射率为R ，Harcher 给出了1、2两组的透射光强分别为： 222110222()[1()sin ]11T R I I R R β-=+-- （1）221I R I = （2）这里I0是入射光强，T 是透射率，β是往返一次所形成的位相差，即222/n L βπλ= （3）n2是腔内介质的折射率。

实验十三 氦氖激光束光斑大小和发散角测量一、激光原理概述1．普通光源的发光——受激吸收和自发辐射普通常见光源的发光（如电灯、火焰、太阳等的发光）是由于物质在受到外来能量（如光能、电能、热能等）作用时，原子中的电子就会吸收外来能量而从低能级跃迁到高能级，即原子被激发。

激发的过程是一个“受激吸收”过程。

处在高能级（E2）的电子寿命很短（一般为10－8～10－9秒），在没有外界作用时会自发地向低能级（E1）跃迁，跃迁时将产生光（电磁波）辐射。

辐射光子能量为12E E h −=ν这种辐射称为自发辐射。

原子的自发辐射过程完全是一种随机过程，各发光原子的发光过程各自独立，互不关联，即所辐射的光在发射方向上是无规则的射向四面八方，另外位相、偏振状态也各不相同。

由于激发能级有一个宽度，所以发射光的频率也不是单一的，而有一个范围。

在通常热平衡条件下，处于高能级E 2上的原子数密度N 2，远比处于低能级的原子数密度低，这是因为处于能级E 的原子数密度N 的大小随能级E 的增加而指数减小，即N∝exp(-E/kT)，这是著名的波耳兹曼分布规律。

于是在上、下两个能级上的原子数密度比为]/)(exp[/1212kT E E N N −−∝式中k 为波耳兹曼常量，T 为绝对温度。

因为E 2>E 1，所以N 2<N 1。

例如，已知氢原子基态能量为E 1＝－13.6eV，第一激发态能量为E 2=-3.4eV，在20℃时，kT≈0.025eV，则0)400exp(/12≈−∝N N可见，在20℃时，全部氢原子几乎都处于基态，要使原子发光，必须外界提供能量使原子到达激发态，所以普通广义的发光是包含了受激吸收和自发辐射两个过程。

一般说来，这种光源所辐射光的能量是不强的，加上向四面八方发射，更使能量分散了。

2.受激辐射和光的放大由量子理论知识了解，一个能级对应电子的一个能量状态。

电子能量由主量子数n(n=1,2,…)决定。

实验 8 He —Ne 激光器光束强度分布及其发散角的测量一、实验目的1．熟悉基横模光束特性2．掌握TEM 00模高斯光束强度分布的测量方法和鉴别 3．测量He-Ne 激光器的远场发射角二、实验原理He －Ne 激光器的模式（指横模）和远场发散角是激光器的基本参数之一。

在激光准直、导航等许多应用中使用的He －Ne 激光器，既要求是TEM ，有要求激光束具有很好的方向性和准直性。

而激光器的远场发散角越小，输出光束准直距离越长，即准直性越好。

我们能够把共焦腔基模光束的空间分布情况，用如下的空间曲线方程表示：222221(0)()x y z L Zω+−= (1)式中， （0）是Z ＝0处基模光斑半径，也就是高斯光束的束腰半径。

TEM 模光束沿X 轴是按双曲线规律变化的，包含Z 轴的任何一小平面，如XZ 平面内，光束传播轨迹是两条双曲线包围部分，如图l 所示。

在垂直于Z 轴的平面内是一个圆，在横截面内，其光强分布是高斯型的。

圆的大小就是基模光斑半径 （z ）：ω（z＝ω （2） ω（z ）代表在Z 处光斑半径，即光强度下降到中心强度的l ／e 2时，对应的半径r =221/2()()x y z ω+=。

由此可见，光斑半径ω（z ）随|z|增大而增大。

图1 共焦腔基模光束空间分布1 ．TEM 00模式的鉴别鉴别He －Ne 激光器输出光束是否是TEM 模，最简单的方法是让激光束垂直射到距离激光器输出端1米处的白屏上，观察光斑的亮度分布。

若是基模光斑，它是一个圆，中心光强最大，则He －Ne 激光器工作在TEM 模。

精确的方法是用扫描干涉仪，在示波器上观察激光器的输出频谱，如果激光器输出光束是基横模，那么，在示波器上就能观察到同一荧光谱线内各个振荡纵模 C ／2L 的频率间隔的均匀分布。

本实验采用计算机和CCD 摄象机与A/D 采集卡结合，记录下光斑的强度分布，以鉴别它是否是高斯分布，从而确定激光器是否工作在TEM 模。

He-Ne激光器的装调与参数测试He-Ne 激光器的装调与参数测试一、实验目的1、熟悉He-Ne 激光器的模式结构2、了解F-P 共焦球面扫描干涉仪的原理3、掌握He-Ne 激光器的调整方法4、掌握用共焦球面扫描干涉仪观察、测量激光纵模的方法二、实验原理1、He-Ne 激光器的模式结构He-Ne 激光器是最常用的连续工作气体激光器，以结构形式不同可分为内腔式、半内腔式和外腔式激光器，如图1所示。

二反射镜组成光学谐振腔，放电管内充以不同比例的氦气和氖气（激活物质），二电极通过毛细管放电激励激光工作物质，在氖原子的一对能级间造成粒子数反转，输出受激辐射。

由于谐振腔的作用，使受激辐射光在谐振腔内来回发射，多次通过激活介质而不断加强。

如果单程增益大于单程损耗，即满足产生激光的阈值条件时，则有稳定的激光输出。

（1）外腔式（2）半内腔式由于各种因素引起的谱线加宽，使激光介质的增益系数有一频率分布，如图2所示，该曲线称为增益曲线。

对于He-Ne 激光器，氖原子的自发辐射中心波长为632.8nm ，增益线宽约为1500MHz 。

由无源谐振腔理论可知，激光器的谐振腔具有无数多个固有的分立的谐振频率，只有频率落在工作物质增益曲线范围内并满足激光器阈值条件的那些模式，才能形成激光振荡，如图2所示。

如果不采取选模措施，则He-Ne 激光器一般以多模方式工作。

不同的振荡模式具有不同的光场分布。

光腔的模式可以分解为纵模和横模，它们分别代表光腔模式的纵向（即腔轴z 方向）的光场分布和横向（即垂直于z 轴方向的xy平面）的光场分布。

通常用符号TEM mnq 标志不同模式，其中q 为纵模序数，一般为很大的正整数；m 、n 为横模序数，一般为0，1，2。

TEM 00q 代表基横模，它对应的光场分布特点是：在光腔轴线上光振幅最大，从中心到边缘振幅逐渐降落。

每一个q 对应纵向一种稳定的电磁场分布，称为一个纵模。

对于同一阶横模，相邻两纵模间距为Lcmnq q mn q 2)1(= = +其中为腔中介质的折射率，L 为谐振腔的长度。

实验三He-Ne激光器的横模、远场发散角、输出光功率的测量实验目的：掌握检测He-Ne激光器模式、远场发散角的一种方法，并且通过实验对He-Ne激光器的横模分布，光斑大小、发散角、激光功率有一感性认识。

实验原理：激光是六十年代发展起来的一门尖端科学。

激光不同于一般的光，它有四个独有的特性：高度的方向性、极好的相干性、高亮度以及单色性强。

正因为这些宝贵的特点使它在许多技术领域中得到广泛的应用。

He-Ne激光器是气体激光器中最先发明的一种激光器。

由于它结构简单、使用方便、工作可靠、制造比较容易，应用范围广，目前仍是最通用的激光器。

普通的He-Ne激光器基本上是由激光放电管和一对镀有多层介质膜的高反射球面镜组成，在图1中用放置在Z0和-Z0位置上的两个圆弧表示。

这两个反射镜组成激光器的光学谐振腔。

其中一个是全反镜，在工作波长上具有尽可能接近100%的反射率；另一个是输出反射镜，是在工作波长上具有特定透过率的部分反射镜。

反射镜准确调准产生的光束是发散的，如图1所示，也就是说其强度分布由光束的中心向光束边缘逐渐减少。

在光束截面上光通量密度分布是理想的高斯型的，这样的光称为“单模”，也称“TEM00”模式。

TEM00的发散角最小，可聚焦成尺寸最小的光点。

TEM00模是最合适的工作模式。

在图1中，Z0称为高斯光束的共焦参量．．．．，其物理意义待后阐明。

在激光管的中心，即z=0处，光束最细，W称为最小光斑尺寸．．．．．．．．．，或束腰、腰斑．．。

在实验中使用的250mm的He-Ne激光器，激光波长为6328埃，是在可见光谱的红光部分。

一、H e-Ne激光器横模的测定检测激光波长为6328A的He-Ne激光器模式的最简便的方法是直接用眼睛或用放大镜观察距离激光器输出端4m以远的白屏上激光光斑的亮度分布。

此法只能作粗略的检查，要鉴定激光器输出的激光是否是严格的基模，则需要采用更为精确的方法。

在实验中，用硅光电池作探测器件，对激光光斑进行扫描，逐点记录硅光电池的光电流，得到一条激光远场某横截面上的光功率分布曲线。

实验 He-Ne 激光器性能参数的测量一、目的1．了解He-Ne 激光器的结构和各部分的作用；2．改变工作电流，观察电流和输出功率的关系；3．了解F-P 扫描干涉仪的结构和性能，掌握它的使用方法，观察激光He-Ne 激光器的输出频谱；4．学会测量输出激光偏振特性的方法。

二、原理1．激光器的调试原理激光器的调试原理是用LD 发出的光作为基准光线，使He-Ne 激光管放在该基准光线上，然后使耦和输出镜也放在该基准光线上，当激光谐振腔满足谐振条件，才能产生He-Ne 激光。

调整He-Ne 激光器与反射镜的相对位置关系，只有当谐振腔的两个反射镜均以激光器毛细管准直时，激光才有可能产生。

2．He-Ne 激光器的模式结构激光器的谐振腔具有无数个固有的、分离的谐振频率。

不同的谐振模式具有不同的光场分布。

光腔的模式可以分解为纵模和横模，它们分别代表光腔模式的纵向光场分布和横向光场分布。

用模指数q n m ,,可表示它们不同的模式。

由无源谐振腔理论，得 )]}1)(1arccos[()1(22{421R L R L n m q L c mnq --++π+η=ν (1-1) 式中，η为介质折射率；c 为真空中的光速；L 为腔长；1R 和2R 为谐振腔的两反射镜曲率半径；q 为纵模指数，一般为很大的整数；n m ,为横模指数，一般为⋅⋅⋅,2,1,0，当0==n m 时为基横模，其对应光场分布在光腔轴线上的振幅最大，从中心到边缘振幅逐渐减小，当00≠≠n m 或时，称为高阶横模。

当n m ,相同时，即对于同一阶横模，相邻纵模间隔是等间距的，其频率差为：Lc mnq q mn η=ν-ν+2)1( (1-2) 对于不同纵模（即q 值不同），虽对应不同的纵向（沿腔轴线方向）光强分布，但由于不同纵模光强分布差异极小，从光斑图样无法分辩，只能根据不同纵模对应不同频率来分析。

设对于某个纵模，其频率为：q L c q η=ν2，则不同纵模间的频率差q L c q q q ∆η=ν∆∆+2, (1-3)由于各种因素可能引起谱线加宽，使激光介质的增益系数有一频率分布，如图1.1所示，该曲线称为增益曲线。