元件数学模型
- 格式:ppt
- 大小:5.97 MB
- 文档页数:89



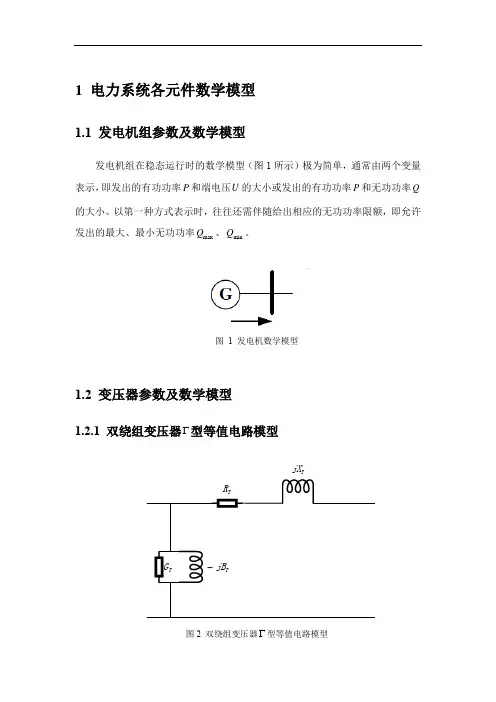
1 电力系统各元件数学模型1.1 发电机组参数及数学模型发电机组在稳态运行时的数学模型(图1所示)极为简单,通常由两个变量表示,即发出的有功功率P 和端电压U 的大小或发出的有功功率P 和无功功率Q 的大小。
以第一种方式表示时,往往还需伴随给出相应的无功功率限额,即允许发出的最大、最小无功功率max Q 、min Q 。
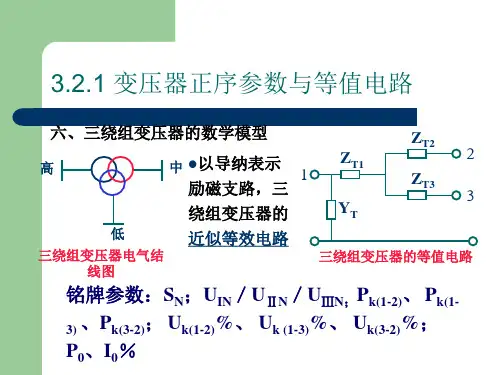
图 1 发电机数学模型1.2 变压器参数及数学模型1.2.1双绕组变压器Γ型等值电路模型TjX 图2 双绕组变压器Γ型等值电路模型双绕组变压器Γ型等值电路模型如图2所示,电路参数通过以下公式计算。
注意,公式中N U 取不同绕组的额定电压,表示将参数归算到相应绕组所在的电压等级(所得所得阻抗/导纳参数都是等值为Y/Y 接线的单相参数);公式中各参数由变压器厂家提供,采用实用单位。
22020210001001000%100k N T Nk NT N T NN T N P U R S U U X S P G U I S B U ⎧∙=⎪⎪⎪%∙=⎪⎪⎨⎪=⎪⎪⎪=∙⎪⎩(1-1) 其中,k P 为短路损耗,k U %为短路电压百分数,0P 为空载损耗,0%I 为空载电流百分数,N U 为归算侧的额定电压,N S 为额定容量 该电路模型一般用于手算潮流中。
1.2.2 双绕组变压器T 型等值电路模型1jX '图 3 双绕组变压器T 型等值电路模型其中,1R 和1X 为绕组1的电阻和漏抗,'2R ,'2X 为归算到1次侧的绕组2 的电阻和漏抗,m R 和m X 为励磁支路的电阻和电抗。
该电路模型一般用于电机学中加深对一二次侧和励磁支路电阻电抗的理解以及手算潮流计算中。
1.2.2 三绕组变压器Z 图4三绕组变压器的等值电路三绕组变压器的等值电路如图3所示,图中,变压器的励磁支路也以导纳表示。
该电路模型一般用于手算潮流计算中。
三绕组变压器的参数计算如下: 电阻:由短路损耗计算()()()1(12)(31)(23)2(23)(12)(31)3(31)(23)(12)121212k k k k k k k k k P P P P P P P P P P P P ---------⎧=+-⎪⎪⎪=+-⎨⎪⎪=+-⎪⎩(1-2) 211222233100010001000k N T Nk N T Nk NT N P U R S P U R S P U R S ⎧∙=⎪⎪⎪∙⎪=⎨⎪⎪∙⎪=⎪⎩(1-3) 其中,k P 为短路损耗,N U 为归算侧的额定电压,N S 为额定容量对于容量比为100/100/50和100/50/100的变压器,厂家提供的短路损耗是小容量绕组达到自身额定电流()/2N I 时的试验数据,计算时应首先将短路损耗折算为对应于变压器额定电流()N I 的值例如,对于100/100/50型变压器,厂家提供的是未经折算的短路损耗'(23)k P -,'(31)k P -,'(12)k P -首先应进行容量归算'(23)(23)'(31)(31)44k k k k P P P P ----⎧=⎪⎨=⎪⎩(1-4) 按新标准,厂家仅提供最大短路损耗max k P ,按以下公式计算电阻:2max (100%)2(50%)(100%)20002k N T N T T P U R S RR ⎧=⎪⎨⎪=⎩(1-5) 其中max k P 为最大短路损耗,N U 为归算侧的额定电压,N S 为额定容量 电抗:由短路电压百分数计算()()()1(12)(31)(23)2(12)(23)(31)3(23)(31)(12)1%%%%21%%%%21%%%%2k k k k k k k k k k k k U U U U U U U U U U U U ---------⎧=+-⎪⎪⎪=+-⎨⎪⎪=+-⎪⎩(1-6) 211222233100100100k N T Nk N T N k NT N U U X S U U X S U U X S ⎧%=⎪⎪⎪%⎪=⎨⎪⎪%⎪=⎪⎩(1-7) 其中,k U %为短路电压百分数,N U 为归算侧的额定电压,N S 为额定容量 注意,厂家提供的短路电压是经过额定电流折算后的数据。






简述元件模型的几种类型及存储方式
元件模型是一种通用的表示电路元件的模型,根据元件的性质和用途不同,可以有多种类型和存储方式。
以下是几种常见的元件模型类型及其存储方式:
1. 线性元件模型:线性元件是指电阻、电感和电容等元件,其模型一般采用电阻、电感和电容的参数值来表示,这些参数值可以直接存储在元件模型中。
2. 非线性元件模型:非线性元件是指二极管、晶体管等具有非线性特性的元件,它们的模型一般采用等效电路模型来表示,例如使用辅助源模型、指数模型或非线性表达式等,这些模型可以通过将元件参数值和数学函数等直接存储在模型中。
3. 数字元件模型:数字元件是指逻辑门、触发器等数字电路中使用的元件,其模型可以根据逻辑功能和时序特性来定义,例如使用真值表、状态转换图或布尔代数表达式等,这些模型的存储方式可以采用存储器或数据表的形式。
4. 动态元件模型:动态元件是指放大器、滤波器等具有频率和相位响应特性的元件,其模型一般采用频域或时域响应函数来表示,例如使用传递函数、频率响应曲线或差分方程等,这些模型可以通过将响应函数和参数值存储在模型中。
元件模型的存储方式可以分为内部存储和外部存储两种:
1. 内部存储:元件模型的参数值和表达式可以直接存储在电路
仿真软件的内部数据库中,以供仿真时调用和计算。
2. 外部存储:元件模型的参数值和表达式可以存储在外部文件中,例如文本文件或二进制文件,这样可以方便地导入和导出模型,或者共享模型资源。
不同的电路仿真软件和设计工具可能有不同的元件模型类型和存储方式,具体的选择可以根据需求和软件支持来确定。