排列与逆序行列式的定义

格式：pptx
大小：396.90 KB
文档页数：27

下载文档原格式

n阶行列式的定义及性质

推论如果行列式有两行(列)完全相同，则此行列式为零
证把这两行互换，有 D D , 故D 0
推论1 行列式中某一行(列)的所有元素的公因子可以提到行列式符号的外面
推论2 若行列式中有两行(列)成比例，则此行列式等于零.
推论3 若行列式中某一行(列)的元素全为零，则此行列式等于零.
证设行列式
a11 D1 kai1 an1
a12 kai 2 an 2
a1n kain ann
是由行列式 D det(aij ) 的第i行中所有的元素都乘以同一数 k得到的. 由行列式的定义知 ( p1 p2 pn ) ( 1) a1 p1 D1
p1 p2 pn
ai 1 pi1 (kaipi )ai 1 pi1
因此当
n 4k
或者 n
4k 1
时，该排列是偶排列；
当n
4k 2
或者
n 4k 3 时，该排列是奇排列。
6
定义在一个排列中，把某两个数的位置互换，而保持其余的数不动，这种对一个排列作出的变动叫做对换. 将相邻两个数对换，叫做相邻对换.
例五级偶排列21354经过2，3对换变成排列31254，容易计算
(21354)=2，所以21354是偶排列.
(2) 在六级排列135246中，共有逆序32，52，54，即
(135246)=3，所以135246是奇排列.
二、排列的逆序数
2. 逆序数计算法：
(q1q2 qn ) ( qi前边的比它
i 1
n
大的数字的个数 )
.例如
(64823517 ) 0 1 0 3 3 2 6 1 16

线性代数第一节排列及其逆序数

第一章行列式第一节排列及其逆序数�引言�排列与逆序数一、引言我们在中学曾经学习过求解二元一次线性方程组⎩⎨⎧=+=+2221212111c x b x a c x b x a （1）当两个方程的未知数系数不成比例，即 2121b b a a ≠时，我们有.b a b ac a c a x ,b a b ac b c b x 122112212122121121−−=−−=（2）为方便记忆，我们引入二阶行列式bc ad db ca −=（3）则（2）可以表示为.b a b ac a c a x ,b a b a b c b c x 221122112221122111==（4）即当（1）的系数行列式0b a b a 2211≠时，（1）的解可以用二阶行列式表示为（4）。

用高斯消元法，对三元一次线性方程组,333323213123232221211313212111⎪⎩⎪⎨⎧=++=++=++b x a x a x a b x a x a x a b x a x a x a （5）我们也可以得到类似的结果。

即如果引入三阶行列式,c c c c c c c c c c c c c c c c c c c c c c c c c c c 322311332112312213322113312312332211333231232221131211−−−++=（6）则当（5）的系数行列式0a a a a a a a a a D 333231232221131211≠=（7）时，方程组（5）的解可以用三阶行列式表示为.a a a a a a a a a b a a b a a b a a x ,a a a a a a a a a a b a a b a a b a x ,a a a a a a a a a a a b a a b a a b x 333231232221131211332312222111211333323123222113121133331232211311123332312322211312113332323222131211===（8）对于n 元一次方程组，是否也有类似于上述（4）、（8）的结果呢？这就是本章要回答的问题。

线性代数第二章方阵的行列式

习题2.2(B) 第1(1)(3)题
2 n阶行列式的性质
本节教学内容
行列式按一行(列)展开定理
Laplace定理
3 展开定理与行列式的计算
3 展开定理与行列式的计算
行列式按一行(列)展开定理三阶行列式的一个计算公式 Mij称为aij的余子式 Aij称为aij的代数余子式
3 展开定理与行列式的计算
线性代数第二章
本章教学内容
1 n阶行列式的定义
2 方阵行列式的性质
3 展开定理与行列式的计算
第二章方阵的行列式
1 n阶行列式的定义
1.排列与逆序数定义由1,2,…,n按任何一种次序排成的有序数组i1 i2… in称为一个n级排列，简称排列. 例 3级排列：123,132,213,231,312,321,共6个性质不同的n级排列共n!个. 排列123，从小到大排，全顺；排列132，3>2,但3排在2之前，即32是一个逆序定义在一个排列i1 i2… in中,若it> is中,但it排在 is之前，则称it与is组成一个逆序.i1 i2… in中所有逆序的总数称为此排列的逆序数, 记为(i1 i2… in).
2 n阶行列式的性质
例 =0 2r1+r2
2 n阶行列式的性质
性质2.5 即
2 n阶行列式的性质
或证由性质2.1及推论2.3得到.
2 n阶行列式的性质
例1
2 n阶行列式的性质
例2
2 n阶行列式的性质
例3 计算行列式解
2 n阶行列式的性质
2.方阵行列式的性质定理2.1 设A,B为n阶方阵，为常数，m为正整数，则 ⑴ A=nA ； ⑵ AB=AB ； ⑶ Am=Am . 注① 一般的A+B≠A+B ； ② 虽然AB≠BA，但AB=BA ； ⑶由⑵推得，下证⑴ ⑵

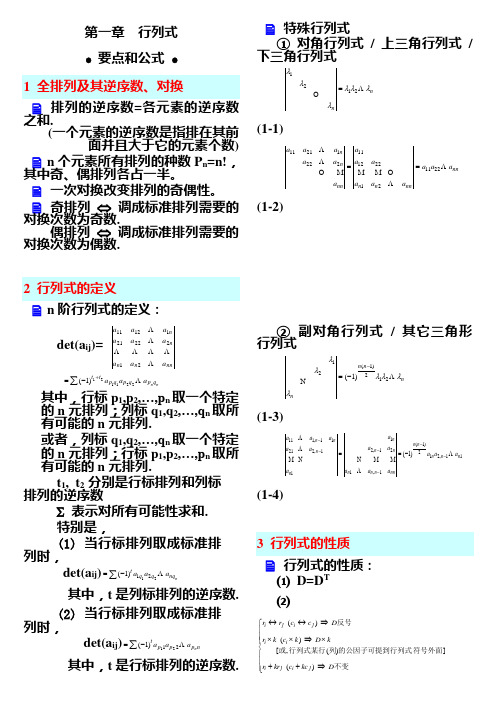
1-习题讲义

第一章行列式 ∙ 要点和公式 ∙1 全排列及其逆序数、对换排列的逆序数=各元素的逆序数之和.(一个元素的逆序数是指排在其前面并且大于它的元素个数) n 个元素所有排列的种数P n =n!，其中奇、偶排列各占一半。

一次对换改变排列的奇偶性。

奇排列 ⇔ 调成标准排列需要的对换次数为奇数.偶排列 ⇔ 调成标准排列需要的对换次数为偶数.2 行列式的定义n 阶行列式的定义：det(a ij )=nnn n n n a a a a a a a a a 212222111211∑+-=nn q p q p q p t t a a a 221121)1(其中，行标p 1,p 2,…,p n 取一个特定的n 元排列；列标q 1,q 2,…,q n 取所有可能的n 元排列.或者，列标q 1,q 2,…,q n 取一个特定的n 元排列；行标p 1,p 2,…,p n 取所有可能的n 元排列.t 1, t 2分别是行标排列和列标排列的逆序数∑ 表示对所有可能性求和. 特别是，(1) 当行标排列取成标准排列时，det(a ij )∑-=nnq q q t a a a 2121)1(其中，t 是列标排列的逆序数. (2) 当行标排列取成标准排列时，det(a ij )∑-=n p p p t na a a 2121)1(其中，t 是行标排列的逆序数.特殊行列式① 对角行列式 / 上三角行列式 / 下三角行列式nnλλλλλλ2121=(1-1)nnnnn n nn n n a a a a a a a a a a a a a a a22112122121122212111==(1-2)② 副对角行列式 / 其它三角形行列式 nn n nλλλλλλ212)1(21)1(--=(1-3)11,212)1(1,121,2111,22111,111)1(n n n n n nnn n n nn nn n n n a a a a a a a a a a a a a a a-------==(1-4)3 行列式的性质行列式的性质： ⑴ D=D T⑵⎪⎪⎪⎩⎪⎪⎪⎨⎧⇒++⨯⇒⨯⨯⇒↔↔不变符号外面的公因子可提到行列式列行列式某行或反号D kc c kr r k D k c k r D c c r r j i j i i i j i j i )( ])(,[ )( )(⑶ 以下都是行列式等于零的充分条件： ①两行(列)完全相同；②某一行(列)的元素全为零；③两(列)的元素对应成比例.⑷ 若行列式的某一行(列)元素都是两数之和，则行列式可分解为两个行列式之和. 重要的行列式计算方法：⑴ 化为三角形行列式 (基本方法)⑵ 分块法①分块对角行列式 / 分块上三角行列式 / 分块下三角行列式B A BOA B O A B O O A ⋅===** (1-5) ②分块副对角行列式 / 其它分块三角形B A BAOO B A O B A O km ⋅-===)1(** (1-6)注意，以上两式中，A,B 分别是k ⨯k 和m ⨯m 的正方形数表.⑶ 拆分法 4 行列式按行(列)展开法则余子式M ij 和代数余子式A ij 的概念改变行列式的某一行(列)元素，不会改变这些元素的余子式和代数余子式.行列式按行(列)展开法则按行ij nk jk ik D A a δ=∑=1，或按列ij nk kj ki D A a δ=∑=1(i=1,2,…,n)(其中D 是行列式的值，⎩⎨⎧≠==ji j i ij ,0 ,1δ)重要的行列式的计算方法：⑴ 降阶展开法 (基本方法) ⑵ 递推法和数学归纳法⑶ 范德蒙德行列式法 ∏≤<≤-----=nn i j j i n nn n n n nx x x x x x x x x x x x x x 111312112232221321)(1111(1-7)5 克拉默法则和有关定理克拉默法则: 对于n 个变量n 个方程的线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++.22112222212*********n n nn n n n n n n b x a x a x a b x a x a x a b x a x a x a 简记为i n j j ij b x a =∑=1 (i=1,2,…,n)若系数行列式D ≠0，则方程组有唯一解：DD x jj = (i=1,2,…,n) 其中D j 是用方程组的常数项b 1, b 2, …, b n 替换系数行列式D 的第j 列得到的行列式。

1-2行列式的定义

τ ( j1 j2 ⋯ jn−1 jn )= ∑ ( jk 后面比jk 小的数的个数 )
k =1
n −1
信息系刘康泽
例4 （1）排列31425 的逆序数为：）排列31425 的逆序数为： τ(31425)=2+0+1+0+0=3 ； (31425)=2+0+1+0+0=3 （2）自然排列 1 2 3 • • • n 的逆序数是0 ；的逆序数是（3）排列 n (n –1) • • • 21 的逆序数为：的逆序数为： n(n − 1) τ = (n − 1) + (n − 2) + ⋯ + 1 + 0 = 2 例5 求排列 ( 2k )1( 2k − 1) 2 ( 2k − 2 ) 3 ( 2k − 3)⋯ ( k + 1) k 的逆序数。的逆序数。解： (2k ) 1 (2k − 1) 2 (2k − 2 ) 3 (2k − 3 )⋯(k + 1) k
信息系刘康泽
第1-2节排列及行列式的定义
信息系刘康泽一、排列及其逆序数
1. n 级排列
由排成的一个有序数组，【定义】 n 个不同的数 1, 2,⋯ , n 排成的一个有序数组，定义】级全排列，级排列。称为一个 n 级全排列，简称 n 级排列。
例1 53214 45238176
1 2 3⋯ n n( n − 1) ⋯ 321
∑
j1 j2 ⋯ jn
表示对表示对所有
信息系刘康泽
【注】 1、以 aij 作为元素的 n 阶行列式有时简记为 det( aij ) 。、 2、行列式表示一个特定的数，它是n行n列的表中、行列式表示一个特定的数，它是行列的表中所有位于不同行、个元素乘积的代数和。所有位于不同行、不同列的n 个元素乘积的代数和。共有 n ! 项求和。项求和。 3、求和项 a1 j1 a2 j2 ⋯ an jn中的行排列总是按自然次、序排列的，且该项的符号取决于列排列的逆序数，即为：序排列的，且该项的符号取决于列排列的逆序数，即为：

线性代数1-2全排列及其逆序数1-3n阶行列式的定义1-4对换

例3 用行列式的定义计算
0 0 0 1 0 0 0 2 0 0 Dn n1 0 0 0 0 0 0 0 0 n
解 Dn 1 t a1,n1a2,n2 an1,1ann
1t 1 2 n 1 n 1t n!, tn 1n 2 21n
01 2L n 3 n 2 0
1234
例3 计算
0 D
4
2
1
0056
0008
解
1234Βιβλιοθήκη 0421D 00
5
6 a11a22a a 33 44 1 4 5 8 160.
0008
同理可得下三角行列式
a11
0 0 0
a21 a22 0 0
an1
an2
an3 ann
a11a22 ann .
例4 证明对角行列式
1 2
因此对换相邻两个元素，排列改变奇偶性 . 再证一般对换的情形 .
设排列为 a1 alab1 bmbc1 cn , 现来对换 a 与b.
a1 al a b1 bm b c1 cn
m 次相邻对换 a1 al ab b1 bmc1 cn
m 1 次相邻对换 a1 al b b1 bm a c1 cn
t 0 1 0 3 1 5.
例2 计算下列排列 nn 1n 2L 321
的逆序数，并讨论它的奇偶性.
解
t 1 2 L (n 2) n 1
nn 1
,
2
当 n 4k,4k 1 时为偶排列；
当 n 4k 2,4k 3 时为奇排列.
第一章行列式
第三节 n 阶行列式的定义
一、概念的引入
1
a a t p1q1 p2q2
a pnqn

1n阶行列式

0+1+0+2+4=7
故排列42531的逆序个数为7，即τ(42531)=7，
因而是奇排列.
返回
上一页下一页
(2) 同理可得：
τ[135…(2n-1)246…(2n)]=0+(n-1)+(n-2)+…+2+1=
n(n 1) 2
所给排列当n=4k或4k+1时为偶排列，当n=4k+2或4k+3
时为奇排列.
把行列式
§3 行列式的性质
的行换成同序数的列,
称为行列式D的转置行列式。
返回
上一页下一页
性质1 行列式与它的转置行列式相等。
证：记
即bij＝aji
(i，j＝1，2，…，n)
按行列式定义
返回
上一页下一页
性质2 互换行列式的两行（列），行列式反号。证
交换第p、q两列，得行列式
返回
上一页下一页
同理可证
返回
上一页下一页
代数余子式的重要性质（行列式按行（列）展开公式）:
返回
上一页下一页
例计算n阶行列式解法一
返回
上一页下一页
例计算n阶行列式
解法二(递推法) 由行列式Dn可知
将Dn按第1列展开
返回
上一页下一页
这个式子对任何n(n2) 都成立,故有
返回
上一页下一页
例利用递推公式法计算解：按第一行展开
Dn＝
返回
上一页下一页
例证明
上面的行列式中，未写出的元素都是0。证: 因为行列式的值为
而排列j1j2…jn只能是n(n－1)…21的排列，故逆序数

§12n阶行列式

n级排列的总数为n·(n-1) ·····2·1=n!。设其中奇排列有p个，偶排列证：有q个。将每一个奇排列都施以同一个对换，由定理1.1可知p个奇排列全部变为偶排列，于是有排列数相等，各为
n! 2
p≤q
；同理，将全部的偶排列都施以同一个对换
q≤ p
，则q个偶排列全部变为奇排列，于是又有。
（2）下面讨论一般情形：设给定的排列为 A i k1 k2 L k s j B
经对换（ i，j ），变为新排列
A j k1 k2 L k s i B
将新排列看作由原排列经一系列相邻对换而得：先将原排列中的数码i向右依次与k1 , k2 ,L , ks 作 s+1次相邻对换得 A k1 k2 Lks j i B，再将j向左依次作s次相邻对换而得新排列；即新排列可由原排列经 2s+1次相邻对换而得，由（1）的结论可知，它改变了奇数次奇偶性，所以它与原排列的奇偶性相反。
，所以得p=q。即奇偶
河南财经政法大学成功学院《线性代数》精品课
二、n阶行列式的定义阶行列式的定义
观察与思考
a11 a12 = a11a22 − a12 a21 a21 a22
a11 a12 a13 a21 a22 a23 =a11a22a33+a12a23a31+a13a21a32 a31 a32 a33 −a11a23a32−a12a21a33−a13a22a31
河南财经政法大学成功学院《线性代数》精品课
举例说明
四阶行列式 a11 a12 a13 a14 a21 a22 a23 a24 D= a31 a32 a33 a34 a41 a42 a43 a44 所表示的代数和中有 4!=24 项. a14a23a31a42行标排列为1234, 元素取自不同的行; 列标排列为4312, 元素取自不同的列, 且N(4312)=5, 即4312为奇排列, 所以元素乘积a14a23a31a42前面应冠以负号, 即− a14a23a31a42为 D的一项.

1.2-2逆序数n阶行列式的定义

特例： 0
an1
0 0 0 ... an1,2 0
... 0 ... 0 ... a3,n2 ... ... 00 00
0 a2,n1
0 ... ... 0
a1n 0
0
n ( n 1)
(1) ...
2
a1n a2,n1...an1,2 an1
0
0
0001
0020 D 例 8、计算四阶行列式 0 3 0 0
的一项，则 i, j, k 应何值？此时，该项的符号是什么？
其它数码不变，得到另一个排列，称为一个对换。如： i1, i2 ,..., is ,..., it ,..., in 经对换(is ,it ) 得：i1,i2 ,...,it ,...,is ,...,in
24153 对换（4，5）得 25143；24153 对换（2，1）得 14253
Th2：任意一个排列经过一个对换后奇偶性改变。如：24153 对换（4，5）得 25143，从一个偶排列变为一个奇排列。
4000
Th4:n 阶行列式 D | aij | 的一般项为
(1) a a ...a ，其中，均为级排 N (i1i2 ...in )N ( j1 j2... jn )
i1 j1 i2 j2
in jn
i1 , i2 ,...,in j1, j2 ,..., jn
n
列。
思考题：若 (1)N (i432 k )N (52 j14) ai5a42a3 j a21ak 4 是五阶行列式 D | aij |
同理上三角行列式：
a11 a12 a13 ... ... a1n
0 a22 a23 ... ... a2n
D 0 0 a33 ... ... a3n a11a22 ...ann

02行列式的定义与性质

02. 行列式的定义与性质一、完全展开式定义2.1 n 阶排列12n j j j共有!n 个n 阶排列.定义2.2 逆(顺)序、逆序数12()n j j j τ；奇排列、偶排列顺序数为12(1)/2()n n n j j j - -τ.例2.1 1)(564312)4432013=++++=τ，所以564312为奇排列. 2)三阶排列及其逆序数、奇偶性如下表：123123123()123231312132213321()022113(1)111111j j j j j j j j j -+++---ττ 三阶行列式123123123111213212223112233122331132132112332122133132231313233()1233(1).j j j j j j j j j a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a =++---=-∑为阶排列τ3)标准排列12n 为偶排列.4)2(21)C (1)/2n n n n ==- τ. 所以，当2,3,6,7,10,11,n = 时，21n 为奇排列；当4,5,8,9,12,13,n = 时，21n 为偶排列.定义2.3 n 阶(方阵的)行列式有完全展开式1212121112121222()1212(1)n n n nn j j j j j nj j j j n n n nna a a a a a a a a a a a =-∑为阶排列τ.矩阵与行列式的区别例2.2 1)下(上)三角(矩阵的)行列式11111122212222(12)1122121122(1).OOn n n nnn n nnnnnn a a a a a a a a a a a a a a a a a a ==-=τ2)对角(矩阵的)行列式 1212|diag(,,,)|n n a a a a a a = . 特别地，有|diag(1,1,,1)|1= .(行列式的规范性) 例2.3 次下(上)三角(矩阵的)行列式11,11112,122,121(21)12,11,111(1)OOn n nn n n n n n n n n nnn n a a a a a a a a a a a a a a a -----==-τ(1)/212,11(1)n n n n n a a a --=- .例2.4 设[]A ij n n a ⨯=的主对角元均为奇数，其他元素均为偶数，求证||0A ≠.二、基本性质变形性质、等于零的性质n 阶行列式就是n 阶方阵的规范的、对行(列)有交错性和多重线性的函数.(——行列式的公理化定义)例2.5a b a cc d b d=. 例2.6 设,A B 均为四阶方阵，12341234[,,,],[,,,]A B αγγγβγγγ==，且||A 1,||2B ==，求||A B +.例2.7 用化三角形法计算数字行列式. 例2.8 箭形行列式三角化.例2.9 先化为箭形行列式，再三角化：计算n 阶行列式11112222n nnn na b a a a a b a D a a a b ++=+.例2.10 快速“打洞”：计算n 阶行列式n a b bb a D b b b a=. 当4,1,2n a b ===时，12341122211111111()/722122212201007772212221200102222122210001i r r r r r r i +++--=--≥-.例2.11 逐行(列)相消：计算n 阶杨辉行列式111,,11,||i j ij n ij i j i j a a a a a a --⎛⎫==⎧ ⎪⎨ ⎪=+⎩⎝⎭.431111111111111111111234012301230123136100136001300134,3,24,31410200141000140001i i i i r r r r r r i i -----==1=.例2.12 求证奇数阶反对称(矩阵的)行列式必为零. 例2.13 计算n 阶行列式111222121212n n n n x x x n x x x n D x x x n++++++=+++，注意对阶数n 做讨论.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

主对角线上元素之积－副对角线上元素之积
因此，上述二元线性方程组的解可表示为
ba a b
1 22
12 2
x 1
a a a a 11 22
12 21
1
b 1
D b2
a 12
a22
x2
a11b2 b1a21
a a a a
11 22
12 21
1 a11 D a21
b1 b2
2020/5/9
线性代数教学课件
53214 53124 回忆：n个数的不同排列共有 n ! 个。
自然排列：按数的大小次序，由小到大排列：
12345. . . n
思考： n级排列中，自然排列只有一种
除此之外，任一n级排列都一定出现较大数码
2020/5/9 排在较小数码之线前性代的数教情学况课件。
10
定义2
1）在一个排列中，若某个较大的数排在某个较小的数前面，就称这两个数构成一个逆序。
a a x 12 21 2 a a x 11 22 2
b1a21 a11b2
得
(a11a22 a a 12 21 ) x2 a11b2 b1a21
同理，得 (a a a a )x b a a b
11 22
12 21 1
1 22
12 2
于是，当 a a a a 0 时，方程组有唯一解
12
法 2： n 级排列 i , i , , i 的逆序数
12
n
(i1 , i2 , , in ) 数 i1 后面比 i1 小的数的个数
数 i2 后面比 i2 小的数的个数
法3：
数 in1 后面比 in1 小的数的个数
(i1 , i2 , , in ) 数 in 前面比 in 大的数的个数
2020/5/9
11 22
12 线21性代数教学课件
2
x b1a22 a12b2
1 a a a a
11 22
12 21
x a11b2 b1a21
2 a a a a
11 22
12 21
为便于记忆，采用记号
aa
D 11
12
a a 21
22
aa
称 D 11 12 为二阶行列式
a a 21
22
ax 23 3
b 2
记
a31 x1 a32 x2 a33 x3 b3
a a a 11
12
13
D a21 a22 a23
a a a 11 22 33 a a a 12 23 31 a a a 13 21 32
aaa
31
32
33
a a a a a a a a a
13 22 31
12 21 33
a a a a
11 22
12 21
其中，数 aij (i 1,2; j 1,2) 称为二阶行列式元素 i 为行标，表明元素位于第 i 行
j 为列标，表明元素位于第 j 列
2020/5/9
线性代数教学课件
3
注： (1) 二阶行列式
a a 11
12
aa
21
22
(2) 运算方法：对角线法则
算出来是一个数。
数 in1 前面比 in1 大的数的个数
2020/5/9
数 i线2 性前代数面教学比课件i2 大的数的个数 13
例2：求排列 3，2，5，1，4 的逆序数。
2）一个排列中出现的逆序的总数称为这个排列的
逆序数，通常记为 (i1 , i2 , , in )
定义3
奇排列：逆序数为奇数的排列。偶排列：逆序数为偶数的排列。
2020/5/9
线性代数教学课件
11
计算排列的逆序数的方法：
法 1：
n个数的任一n级排列，先看数1，看有多少个比1大的数
排在1前面，记为 m1 ;
本章主要讨论以上三个问题。
首先来看行列式概念的形成问题的提出：分析二、三元线性方程组求解过程
引出
二阶、三阶行列式的概念
2020/5/9
线性代数教学课件
1
第一节二阶与三阶行列式
1. 二阶行列式
二元线性方程组：
a11 x1 a21 x1
a12 x2 a22 x2
b1 b2
由消元法，得
a11a21 x1 a11a21 x1
b2
a23
D a
3
21
a 22
b 2
b a a 3
32
33
2020/5/9
a b a 31
3
33
线性代数教学课件
a a b 31
32
3
9
第二节 n阶行列式的的定义
一、排列
定义1：由自然数1，2，······，n 组成的一个有序数组称为一个 n 级排列。
例如： 12345 54321 51234 42135 都是数1，2，3，4，5的排列。
2020/5/9
线性代数教学课件
8
对于三元线性方程组，若其系数行列式
aaa
11
12
13
D a21 a22 a23 0
a a a 31
32
33
可以验证，方程组有唯一解:
D
x1
1
D
其中:
D x 2
2D
D x 3
3D
ba a
1
12
13
a ba
11
1
13
a a b 11
12
1
D1 b2
a22
a23 D2 a21
21
12 2
D
12 (2) 14
11 1
3 12
D
3 24 21
2 21
所以
x1
D1 D
14 2 7
,
D 21 x 2 3
2D 7
2020/5/9
线性代数教学课件
6
2. 三阶行列式类似地，为讨论三元线性方程组
a11
x 1
ax 12 2
ax 13 3
b 1
a21
x 1
ax 22 2
再看有多少个比2大的数排在2前面，记为 m2 ;
继续下去，最后至数n，前面比n大的数显然没有，
记为 mn 0 ;
则此排列的逆序数为 m m m
1
2
n
例1 ( 42135 ) 2 11 4
是偶排列。
( 54312 ) 3 3 2 1 9 是奇排列。
2020/5/9
线性代数教学课件
4
aa
综上，令 D 11 12
a a 21
22
D1
b1 b
a12 a
2
22
D2
a11 a
b1 b
21
2
则，
x1
D1 D
D x 2
2D
称 D 为方程组的系数行列式。
2020/5/9
线性代数教学课件
5
例1：解方程组
3 x1 2 2x
1
x2 x
2
12 1
3 2
解：因为 D
3 (4) 7 0
11 23 3aij (i 1,2,3; j 1,2,3) 称为元素
i j 为行标，
2020/5/9
为列标。线性代数教学课件
7
注： (1) 三阶行列式算出来也是一个数。 (2) 运算方法：对角线法则
例： 2 0 1 1 4 1
1 8 3
2 (4) 3 0 (1) (1) 11 8 1 (4) (1) 0 1 3 2 (1) 8 24 8 4 16 4