第六章 土压力
- 格式:doc
- 大小:140.00 KB
- 文档页数:10

第六章 土压力和挡土墙一、名 词 释 义1.挡土墙:用来支撑天然或人工土坡,防止土体滑坍的构筑物。
2.土压力:墙后填土的自重或填土表面上的荷载对墙产生的侧向压力。
3.刚性挡土墙:指用砖石或混凝土所筑成的断面较大、在土压力作用下仅能发生整体平移或转动、墙身挠曲变形可忽略不计的挡土墙。
4.柔性挡土墙:挡土结构物自身在土压力作用下发生挠曲变形,结构变形影响土压力的大小和分布,这种类型挡土结构物称为柔性挡土墙。
5. 重力式挡土墙:依靠墙本身重量维持其抗倾覆和抗滑移稳定性的刚性挡土墙。
6. 静止土压力:挡土墙在墙后填土的推力或其他外力作用下,不发生任何移动或滑动,这时墙背上的土压力,称为静止土压力。
7. 主动土压力:挡土墙受到墙后填土的作用产生离开填土方向的移动,当移动量足够大,墙后填土土体处于极限平衡状态时,墙背上的土压力称为主动土压力。
8.被动土压力:挡土墙受外力作用向着填土方向移动,挤压墙后填土使其处于极限平衡状态时,作用在墙背上的土压力称为被动土压力。
9.朗肯土压力理论:根据半空间的应力状态和土的极限平衡条件得出土压力的计算方法。
10.临界深度:对墙后填土为粘性土的挡土墙,若离填土面某一深度处的主动土压力等于零,该深度称为临界深度。
11. 库仑土压力理论:是根据墙后土体处于极限平衡状态并形成一滑动楔体时,从楔体的静力平衡条件得出土压力的理论。
12.坦墙:墙后土体破坏时,滑动土楔不沿墙背滑动,而沿第二滑裂面滑动的墙背比较平缓的挡土墙。
二、填 空 题1. 根据墙的位移情况和墙后土体所处的应力状态,土压力可分为 、和被动土压力三种。
Δ,与产生被动土压力所需的墙身 2.在相同条件下,产生主动土压力所需的墙身位移量aΔ。
位移量,的大小关系是p3.在挡土墙断面设计验算中考虑的主要外荷载是 。
4.挡土墙按其刚度及位移方式可分为 、 和临时支撑三类。
5.根据朗肯土压力理论,当墙后土体处于主动土压力状态时,表示墙后土体单元应力状 态的应力圆与土体抗剪强度包线的几何关系是 。




第六章 挡土结构物上的土压力第一节 概述第五章已经讨论了土体中由于外荷引起的应力,本章将介绍土体作用在挡土结构物上的土压力,讨论土压力性质及土压力计算,包括土压力的大小、方向、分布和合力作用点,而土压力的大小及分布规律主要与土的性质及结构物位移的方向、大小等有关,亦和结构物的刚度、高度及形状等有关。
一、挡土结构类型对土压力分布的影响定义:挡土结构是一种常见的岩土工程建筑物,它是为了防止边坡的坍塌失稳,保护边坡的稳定,人工完成的构筑物。
常用的支挡结构结构有重力式、悬臂式、扶臂式、锚杆式和加筋土式等类型。
挡土墙按其刚度和位移方式分为刚性挡土墙、柔性挡土墙和临时支撑三类。
1.刚性挡土墙指用砖、石或混凝土所筑成的断面较大的挡土墙。
由于刚度大,墙体在侧向土压力作用下,仅能发身整体平移或转动的挠曲变形则可忽略。
墙背受到的土压力呈三角形分布,最大压力强度发生在底部,类似于静水压力分布。
2.柔性挡土墙当墙身受土压力作用时发生挠曲变形。
3.临时支撑边施工边支撑的临时性。
二、墙体位移与土压力类型墙体位移是影响土压力诸多因素中最主要的。
墙体位移的方向和位移量决定着所产生的土压力性质和土压力大小。
1.静止土压力(0E )墙受侧向土压力后,墙身变形或位移很小,可认为墙不发生转动或位移,墙后土体没有破坏,处于弹性平衡状态,墙上承受土压力称为静止土压力0E 。
2.主动土压力(a E )挡土墙在填土压力作用下,向着背离填土方向移动或沿墙跟的转动,直至土体达到主动平衡状态,形成滑动面,此时的土压力称为主动土压力。
3.被动土压力(p E )挡土墙在外力作用下向着土体的方向移动或转动,土压力逐渐增大,直至土体达到被动极限平衡状态,形成滑动面。
此时的土压力称为被动土压力p E 。
同样高度填土的挡土墙,作用有不同性质的土压力时,有如下的关系:p E >0E > a E在工程中需定量地确定这些土压力值。
Terzaghi (1934)曾用砂土作为填土进行了挡土墙的模型试验,后来一些学者用不同土作为墙后填土进行了类似地实验。

第六章土压力和挡土墙名词解释:1、挡土墙:用来支撑天然或人工土坡,防止土体滑坍的构筑物。
2、土压力:墙后填土的自重或填土表面上的荷载对墙产生的侧向压力3、静止土压力:挡土墙在墙后填土的推力或其他外力作用下,不发生任何移动或滑动,这时墙背上的土压力,称为静止土压力。
4、主动土压力:挡土墙受到墙后填土的作用产生离开填土方向的移动,当移动量足够大,墙后填土土体处于极限平衡状态时,墙背上的土压力称为主动土压力。
5、被动土压力:挡土墙受外力作用向着填土方向移动,挤压墙后填土使其处于极限平衡状态时,作用在墙背上的土压力称为被动土压力。
6、朗肯土压力理论:根据半空间的应力状态和土的极限平衡条件得出土压力的计算方法。
7、临界深度:对墙后填土为粘性土的挡土墙,若离填土面某一深度处的主动土压力等于零,该深度称为临界深度。
8、库仑土压力理论:是根据墙后土体处于极限平衡状态并形成一滑动楔体时,从楔体的静力平衡条件得出土压力的理论。
填空题1、根据墙的位移情况和墙后土体所处的应力状态,土压力可分为、和被动土压力三种。
2、在相同条件下,产生主动土压力所需的培身位移量Δa与产生被动土压力所需的墙身位移量Δp的大小关系是。
3、在挡土墙断面设计验算中考虑的主要外荷载是。
4、挡土墙按其刚度及位移方式可分为——、——和临时支撑三类。
5、根据朗肯土压力理论,当墙后土体处于主动土压力状态时,表示墙后土体单元应力状态的应力圆与土体抗剪强度包线的几何关系是——。
6、根据朗肯土压力理论,当墙后土体处于被动土压力状态时,表示墙后土体单元应力状态的应力圆与土体抗剪强度包线的几何关系是————。
7、挡土墙墙后土体处于朗肯主动土压力状态时,土体剪切破坏面与竖直面的夹角为——;当墙后土体处于朗肯被动土压力状态时,土体剪切破坏面与水平面的夹角为——。
8、若挡土墙墙后填土抗剪强度指标为c、Ф,则主动土压力系数等于——,被动土压力系数等于——。
9、墙后为粘性填土时的主动土压力强度包括两部分:一部分是由土自重引起的土压力,另一部分是由——引起的土压力。
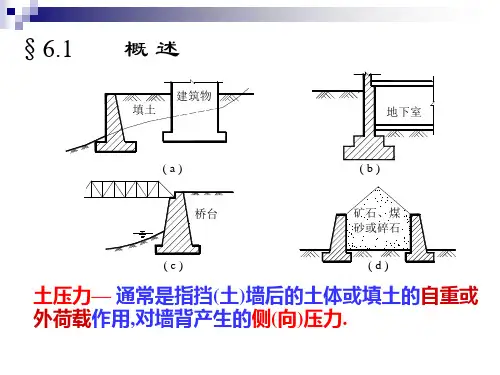




第六章 土压力第一节 土压力的概念一、名词解释1.土压力:是指挡土结构物背后的填土因自重或外荷载作用对墙背产生的侧向压力。
2.主动土压力:当挡土墙在墙后填土作用下,离开土体方向移动或转动,至土体达到极限平衡状态时,作用在墙上的土压力称为主动土压力。
3.静止土压力:当挡土结构物在土压力作用下无任何移动或转动,墙后土体由于墙背的侧限作用而处于弹性平衡状态时,墙背所受的土压力压力称为静止土压力。
4.被动土压力:挡土墙在外力作用下,墙体向填土方向平移或转动,至土体达到极限平衡状态时,作用在挡土墙上的土压力称为被动土压力。
二、填空题1.静止土压力 主动土压力 被动土压力 2.极限平衡 滑裂面 最小 3.增加 极限平衡 最大三、选择题1.A 2.C 3.C 4.B 5. B 6. C 7. B四、判断题1.√ 2.× 3.× 4.√ 5.√ 6.√五、简答题简述挡土墙位移对土压力的影响?答:挡土墙是否发生位移以及位移方向和位移量,决定了挡土墙所受的土压力类型,并据此将土压力分为静止土压力、主动土压力和被动土压力。
挡土墙不发生任何移动或滑动,这时墙背上的土压力为静止土压力。
当挡土墙产生离开填土方向的移动,移动量足够大,墙后填土体处于极限平衡状态时,墙背上的土压力为主动土压力。
当挡土墙受外力作用向着填土方向移动,挤压墙后填土使其处于极限平衡状态时,作用在墙背上的土压力为被动土压力。
挡土墙所受的土压力随其位移量的变化而变化,只有当挡土墙位移量足够大时才产生主动土压力和被动土压力,若挡土墙的实际位移量并未达到使土体处于极限平衡状态所需的位移量,则挡土墙上的土压力是介于主动土压力和被动土压力之间的某一数值。
六、计算题答案:166.5KN/m 解:()022030sin 165.182121-⨯⨯⨯==KH P γ=166.5KN/m第二节 朗肯土压力理论一、填空题1.竖直、光滑 2.墙背直立,光滑,墙后填土面水平,理想塑性体,极限平衡 3.245ϕ-,245ϕ-4.相切 5.相切 6.土的粘聚力 7. 90.4 ;1.55二、选择题1.C 2.D 3.A四、判断题1.× 2.× 3.× 4. 5.√五、简答题1. 答:朗肯研究自重应力作用下,半无限土体内各点的应力从弹性平衡状态发展为极限平很状态的条件,提出计算挡土墙土压力的理论。
第六章挡土结构物上的土压力第一节概述第五章已经讨论了土体中由于外荷引起的应力,本章将介绍土体作用在挡土结构物上的土压力,讨论土压力性质及土压力计算,包括土压力的大小、方向、分布和合力作用点,而土压力的大小及分布规律主要与土的性质及结构物位移的方向、大小等有关,亦和结构物的刚度、高度及形状等有关。
一、挡土结构类型对土压力分布的影响定义:挡土结构是一种常见的岩土工程建筑物,它是为了防止边坡的坍塌失稳,保护边坡的稳定,人工完成的构筑物。
常用的支挡结构结构有重力式、悬臂式、扶臂式、锚杆式和加筋土式等类型。
挡土墙按其刚度和位移方式分为刚性挡土墙、柔性挡土墙和临时支撑三类。
1.刚性挡土墙指用砖、石或混凝土所筑成的断面较大的挡土墙。
由于刚度大,墙体在侧向土压力作用下,仅能发身整体平移或转动的挠曲变形则可忽略。
墙背受到的土压力呈三角形分布,最大压力强度发生在底部,类似于静水压力分布。
2.柔性挡土墙当墙身受土压力作用时发生挠曲变形。
3.临时支撑边施工边支撑的临时性。
二、墙体位移与土压力类型墙体位移是影响土压力诸多因素中最主要的。
墙体位移的方向和位移量决定着所产生的土压力性质和土压力大小。
1.静止土压力(0E )墙受侧向土压力后,墙身变形或位移很小,可认为墙不发生转动或位移,墙后土体没有破坏,处于弹性平衡状态,墙上承受土压力称为静止土压力0E 。
2.主动土压力(a E )挡土墙在填土压力作用下,向着背离填土方向移动或沿墙跟的转动,直至土体达到主动平衡状态,形成滑动面,此时的土压力称为主动土压力。
3.被动土压力(p E )挡土墙在外力作用下向着土体的方向移动或转动,土压力逐渐增大,直至土体达到被动极限平衡状态,形成滑动面。
此时的土压力称为被动土压力p E 。
同样高度填土的挡土墙,作用有不同性质的土压力时,有如下的关系:p E >0E > a E在工程中需定量地确定这些土压力值。
Terzaghi (1934)曾用砂土作为填土进行了挡土墙的模型试验,后来一些学者用不同土作为墙后填土进行了类似地实验。
课程辅导 >>> 第七章、土压力
第七章土压力
一、内容简介
土压力是指土体作用在支挡结构上的侧向压力。
土压力的大小与支挡结构位移的方向和大小有密切的关系,其中静止土压力、主动土压力和被动土压力是实际工程中最常用到的三种土压力。
静止土压力的计算方法由弹性半无限体的计算公式演变而来,而主动土压力和被动土压力所对应的都是土体处于破坏(或极限平衡)状态时的土压力,因此其计算公式的建立与土的强度理论密切相关。
主动和被动土压力的常用计算方法主要是 Rankine 土压理论和 Coulomb 土压理论计算,前者由土中一点的极限平衡条件即 Mohr-Coulomb 准则建立计算公式,后者则利用滑动土楔的静力平衡条件推得,其中土体滑面上法向和切向力之间的关系所反映的实际就是 Coulomb 定律。
二、基本内容和要求
1 .基本内容
( 1 )土压力的概念;
( 2 )土压力的分类及与挡土墙位移的关系;
( 3 )静止土压力的计算;
( 4 ) Rankine 土压力理论及计算;
( 5 ) Coulomb 土压力理论及计算。
2 .基本要求
★ 概念及基本原理
【掌握】静止土压力;主动土压力;被动土压力;墙体位移与墙后土压分布的关系;静止土压理论基本假设; Rankine 土压理论基本假设; Coulomb 土压理论基本假设。
★ 计算理论及计算方法
【掌握】静止土压计算公式及计算;墙背垂直、土面水平且作用有均匀满布荷载、墙后土由不同土层组成时 Rankine 土压计算公式及公式推导、计算;墙背及土面为平面时的 Coulomb 土压计算。
【理解】墙背及土面为平面时 Coulomb 土压力计算公式及推导过程。
三、重点内容介绍
1 .土压力与位移的关系及土压力的类型
土压力是指土体作用在支挡结构上的侧向压力,其大小及分布规律受多种因素影响,对同一结构及土体,土压力的大小主要取决于支挡结构位移的方向和大小。
图 7-1 所示为土压力与刚性挡墙位移(移动或转动)之间的关系。
在工程应用中,常用的土压力类型有以下三种:
图 7-1 土压力与位移之间的关系
( 1 )静止土压力:挡土墙不发生位移时所对应的土压力。
( 2 )主动土压力:挡土墙在土压力作用下离开土体向前位移时,土压力随之减少。
当位移达到某一量值后,墙后土体达到主动极限平衡状态,土压力不再随位移的增大而减小,此时,作用在墙背的土压力称为主动土压力。
( 3 )被动土压力:挡土墙在外力作用下推挤土体向后位移时,作用在墙上的土压力随之增加。
当位移达到某一量值后,墙后土体达到被动极限平衡状态,土压力不再随位移的增大而增加,此时,作用在墙上的土压力称为被动土压力。
通常,达到主动土压所需的相对位移ρ/H 为 0.1 ~ 0.5% ;而达到被动土压所需的的相对位移ρ/H 为 1 ~ 5% ,这是一个较大的值,在实际工程中是不容许发生的,因此设计时常按被动土压力的30%~50% 来设计挡土结构。
显然,被动土压力 > 静止土压力 > 主动土压力。
3 .静止土压力计算
计算时,假设竖向压力与半无限弹性体中铅垂面上的竖向压力相同,即
( 7-1 )若土压力与铅垂面上的水平应力相同,则有
( 7-2 )
式中称为土的侧压力系数或静止土压力系数。
亦可按经验公式计算,这里略去其具体公式。
图 7-2 所示为静止土压力分布的分布图,其中墙高为H ,其合力为
( 7-3 )
图 7-2 静止土压力分布
对主、被动土压,可按计算,这是两个最有名的经典理论,目前在工程中仍得到广泛应用。
4 . Rankine 土压力理论
( 1 )基本假设
① 墙背光滑(无剪应力);
② 墙后土体中的土压(应力)分布与对应的半无限体中的应力分布相同;
③ 墙后土体处于极限平衡状态,其破坏准则为 Mohr - Coulomb 准则。
( 2 )主动土压力
墙后土体处于极限平衡状态,且由墙体的位移方向可知,竖向应力为大主应力,主动土压力
为小主应力,将 Mohr —Coulomb 准则中的和分别以和替换,则可得到主动土压力的计算公式为。
( 7-3 )
式中
( 7-4 )
进一步,可得到以下结论:
① 墙后土体 z 0 深度以上,土发生开裂,墙与土脱离。
其中
( 7-5 )② 对无粘性土,有:
( 7-6 )
③ 由于自重应力为大主应力,故破裂面与地面的夹角为。
④ 若墙后土体的表面作用有满布均匀荷载,则竖向应力为,作为大主应力代入
Mohr — Coulomb 准则,可得
( 7-7 )上述内容示于图 7-3 。
图 7-3 Rankine 主动土压力(时)
( 3 )分层土及土中有地下水时主动土压力计算
首先考虑无地下水的情况。
以无粘性土为例,其计算简图见图 7-4 。
显然,其主动土压力可按下式计算
( 7-8 )
其中为土的竖向应力。
因此,计算时可先确定的分布,然后各土层乘以相应的,即可
得到相应的。
注意到,在各土层的交界面处,虽然竖向应力是相等的,但由于不等,故主动
土压力也不相等,挡墙背后的呈阶梯状分布。
若墙后土层中存在地下水,通常可采用两种方法计算,即水土合算法和水土分算法:前者计算土压力时,将土的重度取为饱和重度,即土、水合起来对挡墙产生土压力,水土合算法多用于粘性土;后者采用浮重度计算土压力,而孔隙水的作用按静水压计算,这种水土分算法多用于砂等无粘性土,如图
7-4 中所示。
图 7-4 分层土及土中有地下水时的主动土压力
(4) 被动土压力
被动土压力计算公式建立的原理与主动土压力相似。
所不同的是,根据其土体的变形特点,自重应力
为小主应力,而被动土压力为大主应力。
被动土压力的计算公式为
( 7-9 )式中
( 7-10 )
图 7-5 Rankine 被动土压力(时)
注意到,破坏面与土面的夹角为。
分层土及有地下水时的计算原理同主动土压力。
5 . Coulomb 土压力理论
( 1 )基本假设
① 挡土墙是刚性的,墙后土为无粘性土。
② 当挡墙发生一定位移时,墙后形成一滑动楔体,滑动面为平面(与实际情况不完全相符,但可大大简化计算工作,且可满足工程要求)。
( 2 ) Coulomb 主动土压力计算
图 7-6 Coulomb 主动土压力
如图 7-6 所示,设挡土墙高为H ,墙背俯斜,与垂线的夹角为,墙后土体为无粘性土,土体表面与水平线夹角为b ,墙背与土体的摩擦角为d 。
挡土墙在土压力作用下向离开土体的方向位移(平
移或转动),最终使土体处于极限平衡状态,墙后土体形成一滑动土楔,其滑裂面与水平面成角。
取滑动土楔为隔离体,作用在滑动土楔上的力有:土楔的自重G ,滑裂面上的反力和墙背面对土
楔的反力(土体作用在墙背上的土压力与大小相等方向相反)。
注意到:主动土压时,土楔
向下滑动,故土楔在墙背及滑面上所受的摩擦阻力向上,相应地,合力、在法线以下。
由于土楔处于平衡状态,故G 、、三力必形成一个封闭的力矢三角形,应用正弦定理可得
( 7-11 )
式中。
由上式尚无法确定,因为式中的是待定的。
研究结果表明,在所有可能的滑面中,使为最大值的滑面是真正的滑面。
令
可确定出,再带回式( 7-11 ),即可得到主动土压力的表达式。
这里,我们人为地假设挡墙
上的土压力呈三角形分布,则可表示为
( 7-12 )
式中
( 7-13 )
( 3) Coulomb 被动土压力
注意到此时土楔是向上滑动的,故在墙面和滑面上所受的摩擦力向下,相应地,、在法线之上,如图 7-7 所示。
由土楔的平衡可得
( 7-14 )
式中。
在所有可能的滑面中,使为最小值的滑面是真正的滑面。
由
得
( 7-15 )
其中
( 7-16 )
图 7-7 Coulomb 被动土压力
6 . Rankine 土压理论与 Coulomb 土压理论的简单比较
( 1 )分析方法
二者均是求解墙后土体达到极限状态时的土压力,即主动土压和被动土压。
但所采用的方法不同。
Rankine :将墙后土体视作半无限体中的一部分,且处于极限平衡状态,由土中一点的极限平衡条件计算土压力,计算理论更为严密
Coulomb :研究对象为墙后滑动楔体,并将其视为刚性(故所得到的是力而不是应力),滑动面上的作用力处于极限状态,由此建立土压力的计算公式。
( 2 )基本假定及适用范围
Rankine :墙背光滑,土面为平面。
Coulomb :无粘性土,墙背可有摩擦,土面可为任意形状。
( 3 )在特定情况下(墙面光滑,铅垂,土面水平),两者的计算结果相同,说明两种理论之间具有一定的共性。