三相电路瞬时无功功率理论首先1983年由赤木泰文提出,此后该理论经不断研究逐渐完善。赤木最初提出的理
- 格式:doc
- 大小:369.00 KB
- 文档页数:5


基于PQ法的谐波电流与无功电流检测方法设计作者:翟文鹏李嗥来源:《科技视界》 2013年第26期翟文鹏李皞(河南登封市电业〈集团〉有限公司,河南登封 452470)【摘要】抑制谐波和提高功率因数是涉及电力电子技术、电气自动化技术和电力系统的一个重大课题。
本文首先对谐波的危害进行了简述,分析了谐波的定义,重点讨论了三相瞬时无功功率理论,并对以此为基础的谐波电流检测法PQ法进行了理论分析和仿真验证。
【关键词】功率因数;谐波抑制;瞬时无功功率0 引言电力电子技术在推动电力系统发展,灵活高效地利用电能的同时,其设备又成为电力系统中最主要的谐波源,同时消耗无功功率[1-2]。
谐波的危害是多方面的,主要体现在:1)对供配电线路的危害:主要是影响线路的稳定运行和电能质量;2)对电力设备的危害:包括对电力电容器的危害、对电力变压器的危害和对电力电缆的危害;3)对用电设备的危害:包括对电动机的危害、对低压开关设备的危害和对弱电系统设备的干扰。
4)对人体和电力测量准确性的影响:目前采用的电力测量仪表当谐波较大时将产生计量混乱,测量不准确。
谐波污染对电力系统安全、稳定、经济运行构成潜在的威胁,给周围的电器环境带来极大影响并对人体健康存在潜在危害,被公认为电网的危害和人体生命的杀手。
1 电力谐波的定义目前国际普遍定义谐波为:谐波是一个周期电气量正弦波分量,其频率为基波频率的整数倍[3]。
以正弦波电压为例,可以表示式(1):式中U是电压有效值,θ是初相角,ω是角频率,T为周期;对于周期为T的非正弦波信号,在满足狄里赫利的条件下,可分解为如式(2)的傅立叶级数。
PQ法的理论基础是三相瞬时无功功率理论。
三相电路瞬时无功功率理论最早在1983年由赤木泰文提出,它是以瞬时实功率P和瞬时虚功率Q的定义为基础。
该理论突破了传统的以平均值为基础的功率定义,系统的定义了瞬时有功功率、瞬时无功功率等瞬时功率量。
当需同时用于补偿谐波和无功时,只需断开图3中计算q的通道即可。
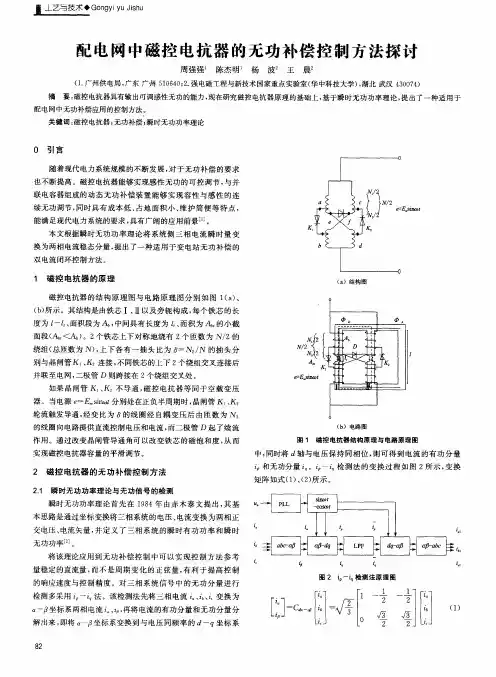



单相级联A PF 谐波与无功电流检测的研究雷霄,郭春林,徐永海(华北电力大学电力系统保护与动态安全监控教育部重点实验室,北京102206) 摘要:瞬时无功功率理论在三相电路谐波和无功电流检测中得到了广泛的应用,该理论也适用于单相电路。
对基于该理论的检测方法之一即构造两相电流分量的方法进行了详细的推导,针对现有方法中的不足进行改进,新增了单独的无功电流检测环节,并给出了准确获得各电流量的关键算法。
在采用该检测方法的同时,将10个H 桥级联的拓扑结构应用于单相A PF ,运用倍频载波移相调制技术和电流PI 控制实现A PF 的功能。
大量的仿真分析证明了提出的检测方法的正确性和有效性,A PF 接入系统后的仿真结果表明该装置能够很好地完成谐波及无功电流的补偿功能。
关键词:瞬时无功功率;谐波;无功电流;检测与补偿;级联中图分类号:TM744 文献标识码:AStudy on Detection Method of H armonic and R eactive Current for Single Οphase APFL EI Xiao ,GUO Chun Οlin ,XU Y ong Οhai(Key L aboratory of Power S ystem Protection and D y namic S ecurit yMonitoring and Cont rol of M inist ry of Education ,N orth China Elect ric Power Universit y ,B ei j ing 102206,Chi na )Abstract :The instantaneous reactive power theory has been widely used in harmonic and reactive current detection in three Οphase system.It is also applicable for single Οphase circuit.After a detailed analysis to the shortages in the existing method of constructing two Οphase system based on the foregoing theory ,some im 2provements were presented.A new channel for detecting reactive current was proposed and the key algorithm to obtain the important current components was presented too.With this detection method ,the cascaded to 2pological structure of 10H Οbridges was applied in single Οphase APF.The method of two times f requency car 2ried phase Οshifting SPWM and PI current controller were used to realize the f unction of A PF.The simulation results prove the correctness and effectiveness of the proposed detection method.The simulation results as A PF connecting to the system indicate that with these control methods the proposed A PF can achieve the com 2pensation of harmonic and reactive current commendably.K ey w ords :the instantaneous reactive power ;harmonic ;reactive current ;detection and compensation ;casca 2ded 基金项目:“十一五”国家科技支撑计划项目(2007BAA12B03);高等学校学科创新引智计划项目(B08013) 作者简介:雷霄(1985-),男,硕士研究生,Email :leixiao100@1 引言有源电力滤波器(A PF )具有能够实现动态连续实时补偿,不受电网元件影响等特点,在抑制谐波、提高电能质量方面显示了强大的生命力,其性能好坏与它采用的谐波电流检测方法有很大关系。


科技视界Science&Technology VisionScience&Technology Vision科技视界0引言电力电子技术在推动电力系统发展,灵活高效地利用电能的同时,其设备又成为电力系统中最主要的谐波源,同时消耗无功功率[1-2]。
谐波的危害是多方面的,主要体现在:1)对供配电线路的危害:主要是影响线路的稳定运行和电能质量;2)对电力设备的危害:包括对电力电容器的危害、对电力变压器的危害和对电力电缆的危害;3)对用电设备的危害:包括对电动机的危害、对低压开关设备的危害和对弱电系统设备的干扰。
4)对人体和电力测量准确性的影响:目前采用的电力测量仪表当谐波较大时将产生计量混乱,测量不准确。
谐波污染对电力系统安全、稳定、经济运行构成潜在的威胁,给周围的电器环境带来极大影响并对人体健康存在潜在危害,被公认为电网的危害和人体生命的杀手。
1电力谐波的定义目前国际普遍定义谐波为:谐波是一个周期电气量正弦波分量,其频率为基波频率的整数倍[3]。
以正弦波电压为例,可以表示式(1):式中U是电压有效值,θ是初相角,ω是角频率,T为周期;对于周期为T的非正弦波信号,在满足狄里赫利的条件下,可分解为如式(2)的傅立叶级数。
u(t)=2√U sin(ωt+θ)(1)u(ωt)=a0+∞n=1∑a n cos nωt+b n sin nωt()(2)式中:a0=12π2π0∫u(ωt)d(ωt),a n=1π2π0∫u(ωt)cos nωtd(ωt),bn=1π2π0∫u(ωt)sin nωtd(ωt)。
频率与工频相等的分量称为为基波,频率是基波频率大于1的整数倍的分量称为谐波,其频率为基波频率的整数倍。
2基于PQ法的谐波电流和无功电流检测设计2.1三相瞬时无功功率理论图1琢茁坐标系中的电压,电流矢量PQ法的理论基础是三相瞬时无功功率理论。
三相电路瞬时无功功率理论最早在1983年由赤木泰文提出,它是以瞬时实功率P和瞬时虚功率Q的定义为基础。


三相电路瞬时无功功率理论由日本学者赤木泰文最先提出,理论打破了传统的以平均值为基础的功率定义。
系统的定义了瞬时有功功率p、瞬时无功功率q等瞬时功率量,后人发展了这套理论,提出了瞬时有功电流ip、瞬时无功电流iq等瞬时量;以瞬时无功功率理论为基础,可以得出用于有源电力滤波器(APF)的谐波和无功电流实时检测方法,此方法在工程应用中受到了极大关注。
但是传统的功率理论是建立在平均值基础上的,所有与之有关的矢量分析与理论计算都基于以下两点:l)相互作用的两个矢量频率相等;2)电压和电流在一个完整的周期内符合正弦波波形且所有周期内波形完全一致。
于是,对于需要动态、快速地跟踪补偿谐波或无功功率的场合,传统的功率理论已经不再适用,而日本学者赤木泰文(Akagi)提出的瞬时无功功率理论适应了现代电力电子技术的发展,得到了很好的应用。
_。

电力系统谐波及滤波技术( 2005—09-21 )摘要:主要针对电力系统谐波的危害及其检测分析技术,归纳总结了目前电力系统中进行谐波抑制常用的方法。
我们知道,在电力系统中采用电力电子装置可灵活方便地变换电路形态,为用户提供高效使用电能的手段。
但是,电力电子装置的广泛应用也使电网的谐波污染问题日趋严重,影响了供电质量。
目前谐波与电磁干扰、功率因数降低已并列为电力系统的三大公害。
因而了解谐波产生的机理,研究消除供配电系统中的高次谐波问题对改善供电质量和确保电力系统安全经济运行有着非常积极的意义。
谐波及其起源所谓谐波是指一个周期电气量的正弦波分量,其频率为基波频率的整数倍.周期为T=2π/ω的非正弦电压u(ωt),在满足狄里赫利条件下,可分解为如下形式的傅里叶级数:式中频率为nω(n=2,3…)的项即为谐波项,通常也称之为高次谐波。
应该注意,电力系统所指的谐波是稳态的工频整数倍数的波形,电网暂态变化诸如涌流、各种干扰或故障引起的过压、欠压均不属谐波范畴;谐波与不是工频整倍数的次谐波(频率低于工频基波频率的分量)和分数谐波(频率非基波频率整倍数的分数)有定义上的区别。
谐波主要由谐波电流源产生:当正弦基波电压施加于非线性设备时,设备吸收的电流与施加的电压波形不同,电流因而发生了畸变,由于负荷与电网相连,故谐波电流注入到电网中,这些设备就成了电力系统的谐波源。
系统中的主要谐波源可分为两类:含半导体的非线性元件,如各种整流设备、变流器、交直流换流设备、PWM变频器等节能和控制用的电力电子设备;含电弧和铁磁非线性设备的谐波源,如日光灯、交流电弧炉、变压器及铁磁谐振设备等.国际上对电力谐波问题的研究大约起源于五六十年代,当时的研究主要是针对高压直流输电技术中变流器引起的电力系统谐波问题。
进入70年代后,随着电力电子技术的发展及其在工业、交通及家庭中的广泛应用,谐波问题日趋严重,从而引起世界各国的高度重视。
各种国际学术组织如电气与电子工程师协会(IEEE)、国际电工委员会(IEC)和国际大电网会议(CIGRE)相继各自制定了包括供电系统、各项电力和用电设备以及家用电器在内的谐波标准。
3.1.1 三相电路瞬时无功理论及其应用3.1.1.1 三相电路瞬时无功理论三相电路瞬时无功功率理论的提出始于20世纪80年代,由赤木泰文提出,该理论突破了传统的以平均值为基础的功率定义,系统地定义了瞬时无功功率、瞬时有功功率等瞬时功率量[18]。
设三相电路的电压电流瞬时值分别为c b a c b a i i i u u u ,,,,,。
然后把它们变换到βα-两相正交的坐标系上得到两相瞬时电压βαu u ,及两相瞬时电流βαi i ,,即:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡c b a u u u C u u 32βα(3.1)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡c b a i i i C i i 32βα(3.2)其中 ⎥⎦⎤⎢⎣⎡---=2/32/302/12/1132C (3.3)在图3-1所示的βα-平面上,失量βαu u ,和βαi i ,可以合成为电压失量U 和电流失量I 。
u βαu u u U ϕ∠=+=(3.4)i βαi i i I ϕ∠=+=(3.5)图中三相瞬时有功电流为ϕcos I i p =(3.6)用相瞬时无功电流为ϕsin i i q =(3.7) 其中i u ϕϕϕ-=(3.8)则瞬时有功p 为电压失量U 与瞬时有功电流p i 和乘积;瞬时无功功率q 为电压失量U 和瞬时电无功电流q i 的乘积。
即:p Ui p =(3.9)q Ui p =(3.10)则由(3.6) (3.7) (3.8) (3.9) (3.10)整理得矩阵形式:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡βαβααββαi i C i i u u u u q p pq(3.11)式中⎥⎦⎤⎢⎣⎡-=αββαu u u u C pq 。
再把式(3.1) (3.2)代入(3.11)得c c b b a a i u i u i u p ++=(3.12)[]c b a b a c a b a i u u i u u i u u q )()()(31-+-+-=(3.13)图3-1:βα-坐标图Fig.3-1: Diagram for βα- coordinate由图3-1中投影关系可得p u u ui U u i i p u p ap 22cos βαααϕ+===(3.14)p u u u i U u i i p u p p 22sin βαβββϕ+===(3.15)q u u ui U u i i q u q aq 22sin βαββϕ+=== (3.16)q u u ui U u i i q u q q 22cos βαααβϕ+-=-=-=(3.17)p u u u i u p p 222βααααα+==(3.18)p u u u i u p p 222βαββββ+==q u u u u i u q q 22βαβαααα+==(3.20)q u u u u i u q q 22βαβαβββ+-==(3.21)在(3.15)到(3.17)各式中,在时间坐标下的三相有功电流、无功电流与βα-坐标下的有功电流与无功电流存在以下关系⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡p p cp bp ap i i C i i i βα23(3.22)⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡q q cq bq aq i i C i i i βα23(3.23)在式(3.22)、(3.23)中T3223C C =。
电力有源滤波器谐波检测算法宋秉虎;王明晖【摘要】随着电力电子技术的快速发展,大量的开关器件被应用于电力控制中,给电网带来不可忽视的谐波.在众多谐波补偿装置中,电力有源滤波器是一种比较理想的滤波装置,它可以实时地检测出电网中的谐波电流,由补偿装置发出补偿电流,从而达到谐波抑制的目的.如何快速准确地检测出电网中复杂的谐波电流成为一个重要的研究内容.提出一种基于小波变换的无功电流与谐波检测方法,该方法既能检测稳态信号,又能检测出瞬态变化信号,通过仿真和实验结果,验证了该方法优秀的分析能力.【期刊名称】《电焊机》【年(卷),期】2015(045)007【总页数】7页(P28-34)【关键词】电力有源滤波器;谐波检测;小波变换【作者】宋秉虎;王明晖【作者单位】国网甘肃省电力公司,甘肃兰州730000;中国航天科工集团二院,北京100854【正文语种】中文【中图分类】TG434从20个世纪二三十年代开始,德国首次提出了静态整流器引起的电流波形畸变问题,也正是从那时开始,谐波这一问题引起人们的注意。
谐波是频率为基波整数倍的信号,谐波的存在给电网带来了很多不利的影响,如影响设备正常工作,产生附加损耗,使设备过热,产生误动作,降低设备的寿命等。
随着电力电子技术的发展,大量的开关器件被应用于电源装置和电机调速中,在为工业设备带来高效良好控制手段的同时,也给电网带来了不可忽视的高次谐波。
近几年,针对传统谐波抑制的各种弊端,有源滤波技术被广泛关注。
有源滤波技术的基本原理是从电网中实时检测出谐波电流的信息,由补偿装置发出与谐波电流大小相等、方向相反的补偿电流,从而达到谐波抑制的目的。
电力有源滤波器是一种可以动态补偿电网谐波的装置,弥补了传统谐波抑制的诸多不足,谐波检测算法的选择对于谐波抑制的效果起着至关重要的作用,只有实时准确地检测出当前时刻电网中的谐波并且给予补偿,才能达到良好的谐波抑制效果。
目前,在各种有源滤波设备中,应用最广泛的是基于瞬时无功理论的谐波检测方法,在分离各次谐波、进行谐波分析方面,应用最广泛的是基于快速傅里叶变换的谐波检测方法及其改进。
谐波检测方法谐波检测是谐波问题中的一个重要分支,对抑制谐波有着重要的指导作用,对谐波的分析和测量是电力系统分析和控制中的一项重要工作,也是对继电保护、判断故障点和故障类型等工作的重要前提。
准确、实时地检测出电网中瞬态变化的畸变电流、电压,是众多国内外学者致力研究的目标。
常规的谐波测量方法主要有三种:模拟带通或带阻滤波器的谐波测量;基于傅里叶变换的谐波测量;基于瞬时无功功率的谐波测量。
一、模拟滤波器:最早的谐波检测方法是采用模拟滤波器来实现的。
输入信号经放大后送入一组带通滤波器,滤波器的中心频率f1、f2、…fn是固定的,为工频的整数倍,且f1〈f2…〈fn,然后送多路显示器中显示测量信号中所含谐波成分及其幅值。
该方法的实现电路简单,造价低,输出阻抗低,品质因数易于控制。
但是电路较难设计,误差大,对电网频率波动和电路元件参数很敏感,使得检测出的谐波中含有较多的基波分量,运行损耗大。
二、快速傅立叶变换:随着计算机和微电子技术的发展,开始采用傅立叶分析的方法来检测谐波和无功电流,有离散傅立叶变换(DFT)和快速傅立叶变换(FFT)两种。
这种方法根据采集到的一个电源周期的电流值进行计算,最终得出所需的谐波和无功电流,它可以精确地分析和检测整数次谐波,目前应用比较广泛,技术也相当成熟。
但由于傅立叶变换要进行两次变换,计算量大,计算时间长,所以检测时间比较长。
三、瞬时无功功率理论:1983年日本学者赤木泰文提出的瞬时无功功率理论,即p-q理论解决了谐波和无功功率的瞬时检测和不用储能元件就能实现抑制谐波和无功补偿等问题,从而使得电力有源滤波理论由实验室的理论研究走向工作应用。
根据该理论,可以得到瞬时有功功率p和瞬时无功功率q,p和q中都含有直流分量和交流分量。
由此可得被检测电流的基波分量,将基波分量与总电流相减即得相应的谐波电流。
因为该方法忽略了零序分量,对于不对称系统,瞬时无功的平均分量不等于三相的平均无功。
瞬时无功理论下的无功电流检测方法探讨作者:卞漫娟来源:《智富时代》2018年第10期【摘要】本文通过分析目前常用的各种电力系统无功电流检测方法的优劣,按照不同补偿要求,采用了ip-iq法和Hilbert法两种具体的检测方法。
运用Maflab对两种方法的仿真模型进行了稳态和动态性能分析,最终在工控机硬件平台下进行了验证。
结果表明,这两种算法均能很好地检测出三相系统中的无功电流,从而达到无功补偿的目的。
【关键词】瞬时无功理论;无功电流;检测方法;探讨一、瞬时无功功率理论和无功检测方法在1983年间,赤木泰文提出了著名的三相电路瞬时无功功率理论,这在世界上具有非常重要的影响作用。
具有2种不同的运算方式,主要体现在p,g运算方式与ip,iq法运算。
综合运用两路电压与三路电流信号过程中应当充分利用p,g运算方式,在这种制作过程中应当利用两路电压和三路电流信号,这种运算方式具有很大的优势,同时也具有受电压畸变与三相电压不平衡的缺陷,不可避免地出现了比较大的检测误差。
制作过程中充分运用了正弦信号,以此来实现有效的电压信号。
二、两种检测方法的原理简介1.ip-iq无功电流检测法的原理为了有效降低电压畸变对系统检测中的作用,需要充分运用正余弦发生器与锁相环的作用得到同相位之下的正余弦信号,并基于此数据得到ip-iq数值,进而计算出ip,iq的直流分量,在运算过程中只需要得到基波正序有功分量即可,采用的计算方式是对ip的直流分量ip 进行反变换运算,之后再将得到的数据与补偿之前的电流进行相减处理,从而最终得到相应的补偿电流。
采用这种计算方式是因为只有有功电流才会影响到基波正序有功电流分量,其他因素的影响可以忽略不计。
结合对称分量法中的表达,在本文的研究中把三相三线电力负荷的电流分量ia,ib,ic等几个单元分别进行正序分量组、负序分量组以及零序分量等三个等级的表示。
零序电流分量不在三相三线制电力系统的研究范围之中,结合这一研究成果,可以把系统电流表示成负序分量组与正序分量组两个组成部分。
故弄玄虚的瞬时无功功率理论沈阳万思电力技术研究所标签:无功补偿三相电路瞬时无功功率理论是由日本学者赤木泰文于1983年首先提出来的。
赤木泰文的理论中定义了瞬时实功率p和瞬时虚功率q,因此又称为pq理论。
该理论受到很多人的追捧,并且不断有人为其添砖加瓦。
在pq理论中使用了一系列的矩阵变换,来定义没有物理意义的实电压和虚电压以及实电流和虚电流,并导出瞬时实功率p和瞬时虚功率q。
从而得出可以通过对瞬时值的检测来确定系统无功参数的结论。
其实,赤木泰文的pq理论最终导出的瞬时实功率p和瞬时虚功率q就是在三相完全平衡状态下可以导出的值,也就是说:只有在三相完全平衡的状态下,赤木泰文的pq理论才有正确的结果。
在三相不平衡的状态下,使用赤木泰文的pq理论不会得出正确的结果。
在pq理论中使用一系列的矩阵变换以及定义没有物理意义的实电压和虚电压不过是为了搅浑水,使人们无法一下子看清其中的破绽罢了。
有人比赤木泰文走的更远,不仅发明出新的方法使瞬时无功功率理论应用于不平衡系统,而且应用于三相四线系统,直至单相系统。
更有人发明出新的方法不仅使瞬时无功功率理论应用于纯正弦波系统,而且应用于含谐波系统,直至应用于暂态过渡系统。
所有的这些“新发展”,都得力于矩阵变换这种可以搅浑水的有效工具。
下面我们详细探讨瞬时无功功率理论的问题所在。
一,关于瞬时无功功率的定义由于SVG装置可以实现很高的响应速度,于是人们就开始研究对无功功率的快速检测问题。
在电力系统中基本的物理量定义大都是以平均值为基础的,例如电压有效值U、电流有效值I、有功功率P、无功功率Q、视在功率S等等。
以平均值为基础的定义显然不能满足快速检测的需要,而为了进行快速无功补偿,就需要对无功功率进行快速检测,因此就产生了怎样定义瞬时无功功率的问题,在这里有必要对瞬时与平均进行深入探讨。
在正弦稳态的情况下,设U和I是有效值,则正弦电压和电流可以表示如下:瞬时功率可以表达如下:电流可以分解为有功电流和无功电流,由于有功电流与无功电流有90度的相位差,因此有功电流与无功电流属于正交向量,于是瞬时电流就可以表达为有功电流瞬时值与无功电流瞬时值的代数和。
三相电路瞬时无功功率理论首先1983年由赤木泰文提出,此后该理论经不断研究逐渐完善。
赤木最初提出的理论亦称pq 理论,是以瞬时实功率p 和瞬时虚功率q 的定义为基础,其主要的一点不足是未对有关的电流量进行定义。
下面将要介绍的是以瞬时有功电流p i 和瞬时无功电流q i 为基础的理论体系,以及它与传统功率定义之间的关系。
设三相电路各相电压和电流的瞬时值分别为a e 、b e 、c e 和a i 、b i 、c i 。
为分析问题方便,把它们变换到βα-两相正交的坐标系上研究。
由下面的变换可以得到α、β两相瞬时电压αe 、βe 和α、β两相瞬时电流αi 、βi
⎥⎦⎤⎢⎣⎡e e βα⎥⎦⎤⎢⎣⎡i i βα式中=32C 在图6-1 e e e α+=i i i βα+=式中,e 【定义 cos i i p =ϕsin i i q = (6-6)
式中,i e ϕϕϕ-=。
βα-平面中的p i 、q i 如图6-1所示。
【定义6-2】三相电路瞬时无功功率q (瞬时有功功率p )为电压矢量的模和三相电路瞬时无功电流q i (三相电路瞬时有功电流p i )的乘积。
即
p ei p = (6-7)
q ei q = (6-8)
把式(6-5)、式(6-6)及i e ϕϕϕ-=代入式(6-7)、式(6-8)中,并写成矩阵形式得出
⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡βαβααβ
βαi i C i i e e e e q p pq (6-9) 式中⎥⎦
⎤⎢⎣⎡-=βββα
e e e e C pq 。
把式(6-1)、式(6-2)代入上式,可得出p 、q 对于三相电压、电流的表达式
a a i e p +=([q =3
1从式(【定义q i (瞬i i p p α=i i p p β=i i q q α=i i q q β-=图6-1从定义3(1) 2
22p p p i i i =+βα (6-13a )
222q q q i i i =+βα (6-13b )
αααi i i q p =+ (6-14a )
βββi i i q p =+ (6-14b )
上述性质(1)是由α轴和β轴正交而产生的。
某一相的瞬时有功电流和瞬时无功电流也可分别称为该相瞬时电流的有功分量和无功分量。
【定义6-4】α、β相的瞬时无功功率αq 、βq (瞬时有功功率αp 、βp )分别为该相瞬时电压和瞬时无功电流(瞬时有功电流)的乘积,即 p e e e i e p p 222β
ααααα+== (6-15a ) p e e e i e p p 222βαββββ+== (6-15b )
e e 从定义(1)(2)【定义电流q i α、即
=⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡cp bp ap C i i i =⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡cq bq aq C i i i 式中C 23=把式(6-12)代入式(6-18)、式(6-19)中得
A
p e i a
ap 3= (6-20a ) A p e i b bp 3= (6-20b ) A
p e i c cp 3= (6-20c ) ()A q e e i c b aq -= (6-21a )
()
A
q e e i a c bq -= (6-21b ) ()A q e e i b a cq -= (6-21c ) 式中()()()()
a c c
b b a
c b a a c c b b a e e e e e e e e e e e e e e e A ---++=-+-+-=2222222 从以上各式可得到如下性质:
(1)0=++cp bp ap i i i (6-22a )
0=++cq bq aq i i i (6-22b )
(2)ap i bp i + cp i +【定义i e p ap a a =i e p bp b b =i e p cp c c =i e q aq a a =i e q bq b b =i e q cq c c =定义6-6(1) p p p p c b a =++ (6-26)
(2) 0=++c b a q q q (6-27)
传统理论中的有功功率、无功功率都是在平均值基础或相量的意义上定义的,它们只适用于电压、电流均为正弦波时的情况。
而瞬时无功功率理论中的概念,都是在瞬时值的基础上定义的,它不仅适用于正弦波,也适用于非正弦波和任何过渡过程的情况。
从以上各定义可以看出,瞬时无功功率理论中的概念,在形式上和传统理论非常相似,可以看成传统理论的推广和延伸。
下面分析三相电压和电流均为正弦波时的情况。
设三相电压、电流分别为
t E e m a ωsin = (6-28a )
()2sin πω-=t E e m b (6-28b )
()32sin πω+=t E e m c (6-28c )
()ϕω-=t I i m a sin (6-29a )
()2sin πϕω--=t I i m a (6-29b )
()2sin πϕω+-=t I i m a (6-29c )
利用(
=⎥⎦
⎤⎢⎣⎡E e e βα=⎥⎦
⎤⎢⎣⎡βαI i i m 式中m E 2把式(2
3m E p =
23m E q =令E E =3EI p =3EI q =率p 把式(t I i m p ωϕαsin cos 2= (6-24a )
()2sin sin 2πωϕα-=t I i m q (6-24b )
比较上式和式(6-31)可以看出,α相的瞬时有功电流和瞬时无功电流的表达式与传统功率理论中a 相电流的有功分量和无功分量的瞬时值表达式完全相同。
对于β相及三相中的a 、b 、c 各相也能得出同样的结论。
由上面的分析不难看出,瞬时无功功率理论包容了传统的无功功率理论,比传统理论有更大的适用范围。