§6.3.1数据的表示导学案

《.1数据的表示》第1课时一、学习目标：二、自主学习内容及学法指导：多边形和圆的初步认识E D CB A 班别 组别 姓名学习目标：1、经历从现实世界中抽象出平面图形的过程，感受图形世界的丰富多彩。

2、了解多边形的有关概念，认识多边形的边、内角、顶点、对角线。

认识正多边形。

3、了解圆的有关概念，认识圆的半径、圆弧、圆心角，扇形，会计算圆心角的度数。

任务一：自主先学，认真阅读课本122页和124页的内容，完成以下练习。

〔一〕多边形的有关概念1、.我们熟悉的平面图形中的多边形有_____________等.它们是由一些_______同一条直线上的线段依次_______相连组成的_______图形.2.、如下图，在多边形ABCDE 中，顶点有 ，多边形的边有 ，多边形的内角有 ；多边形的对角线的定义： 的线段叫多边形的对角线。

〔请在图上画出两条对角线〕3、三角形有 个顶点， 条边， 个内角；四边形有 个顶点， 条边， 个内角；五边形有 个顶点， 条边， 个内角；n 边形有 个顶点， 条边， 个内角。

注：没有特别说明，本书说的多边形都是 多边形。

4、正多边形的定义： 。

5、小学学过的以下图形中不可能是正多边形的是( )6、正十二边形的顶点数是____，边数是 ,内角个数有 个。

〔二〕圆的有关概念7、平面上，一条线段绕着它固定的一个端点旋转一周，另一个端点形成的图形叫做 。

固定的端点O 称为 ，OA 称为 。

8、圆上A,B 两点之间的局部叫做_______，记作： ，读作： ； 由一条_______和经过它的端点的两条_______所组成的图形叫做扇形 9.、圆心角的定义： 。

10、请你画一个圆，你是怎么画的？你有多少方法可以画一个圆？你能用一根细绳和笔画出一个圆吗？任务二：生生合作、师生合作，探索疑难1.从以下多边形的同一顶点出发，连接这个顶点与其余各顶点之间的对角线，答复下面问题。

通过画图，发现：从一个四边形的同一个顶点出发，可以画条对角线，可以分割成个三角形。

6。

3．1 频数直方图【学习目标】1.能绘制(或补全）频数分布直方图。

２．由频数分布直方图提供的信息能解决简单的实际问题。

３。

通过学习，体验频数分布直方图的作用,从而激发学生学习数学的热情。

【学习重难点】1。

学会绘制频数分布直方图.2。

掌握频数分布表和直方图的制作方法以及步骤。

【学习过程】一、学习准备：1.有一个含有50个数据的数据组,最小数据是15，最大数据是45，且都是整数，那么这50个数据分为8组时,组距是 ,第１组的下限宜为 ,于是其上限是，而最末一组的上限是。

２．已知数据8、6、10、1３、10、8、7、１0、11、1２、１0、8、9、11、9、12、1０、12、１1、９，在编制频数分布表时，如果组距取为2,那么应分成组,１2~１３这组的频数为，频率为.二、自主探究请先阅读教材Ｐ78—P８１，并完成以下问题.(一)看P80的图6－3,请你分析频数分布直方图的结构是：（1)横轴: 表示分组情况。

每条线段的左端点标明这一组的限，每条线段的两个端点标号之差表示,称之为。

（2）纵轴:表示频数。

(3）条形图:条形图中每一条形是立于上的一个矩形,矩形的宽等于 ,高度对应于。

三、课堂小结：这节课你有什么收获？四、随堂训练1.如图1是１99８年参加国际教育评估的15个国家学生的数学平均成绩的统计图,则平均成绩大于或等于６0分的国家个数是（ ）A.4B.８ C ．10 D.１2２.某校为了了解九年级学生的体能情况,随机抽查了其中的３０名学生，测试了1分钟仰卧起座的次数,并绘制成如图2所示的频数分布直方图,请根据图示计算,仰卧起座次数在１5至20次之间的频率是（ )3．已知在频数分布直方图中各矩形的高之比为2：４:３：1,总数据有３0个，则第二小组的频率为;第四小组的频数为 。

４.在频数分布直方图中，共有7个长方形，已知共有60个数据，如果中间一个长方形的面积等于其它6个长方形面积和的，则中间这一小组的频数为 ,频率为 。

《6.3.1平面向量基本定理》教案1e 2e aOCAB1e 2e aNOB C 的直线，与直线作平行于直线如图，过点OA C 的直线，与直线作平行于直线过点ON OM OC +=则e ON 共线可得，存在实数与例3 如图所示，在△ABC 中，点M 是AB 的中点，且AN →＝12NC →，BN 与CM 相交于点E ，设AB →＝a ，AC →＝b ，试用基底{a ，b }表示向量AE →.[解] 易得AN →＝13AC →＝13b ，AM →＝12AB →＝12a ，由N ，E ，B 三点共线知存在实数m ， 满足AE →＝mAN →＋(1－m )AB →＝13m b ＋(1－m )a .由C ，E ，M 三点共线知存在实数n ， 满足AE →＝nAM →＋(1－n )AC →＝12n a ＋(1－n )b ，所以13m b ＋(1－m )a ＝12n a ＋(1－n )b ，是直角三角形。

用向量方法证明，的中线，是如图，ABC AB CD ABC CD ∆=∆21b DA a CD ==,证明：如图设b a CB b DB b a CA -=-=+=于是则,,()()22b a b a b a CB CA -=-•+=•ABCD 21=因为DA CD =所以2222,DA b CD a ==因为0=•CB CA 所以CB CA ⊥因此是直角三角形。

于是ABC ∆《6.3.1 平面向量基本定理》导学案【学习目标】平面向量基本定理【小试牛刀】思维辨析(对的打“√”，错的打“×”)(1)基底中的向量不能为零向量．( )(2)若a e 1＋b e 2＝c e 1＋d e 2(a ，b ，c ，d ∈R )，则必有a ＝c ，b ＝d .( ) (3)若两个向量的夹角为θ，则当|cos θ|＝1时，两个向量共线．( ) (4)若向量a 与b 的夹角为60°，则向量－a 与－b 的夹角是60°.( ) (5)平面内的任何两个向量都可以作为一个基底．( )(6)若a ，b 不共线，且λ1a ＋μ1b ＝λ2a ＋μ2b ，则λ1＝λ2，μ1＝μ2. ( ) 【经典例题】题型一 平面向量基本定理的理解点拨：(1)两个向量能否作为一个基底，关键是看这两个向量是否共线．若共线，则不能作基底，反之，则可作基底．(2)一个平面的基底一旦确定，那么平面上任意一个向量都可以用这个基底唯一线性表示出来．设向量a与b 是平面内两个不共线的向量，若x 1a ＋y 1b ＝x 2a ＋y 2b ，则⎩⎪⎨⎪⎧x 1＝x 2，y 1＝y 2.(3)一个平面的基底不是唯一的，同一个向量用不同的基底表示，表达式不一样． 例1 如果e 1、e 2是平面α内两个不共线的向量，那么下列说法中不正确．．．的是( ) ①a ＝λe 1＋μe 2(λ、μ∈R )可以表示平面α内的所有向量；②对于平面α内任一向量a ，使a ＝λe 1＋μe 2的实数对(λ，μ)有无穷多个； ③若向量λ1e 1＋μ1e 2与λ2e 1＋μ2e 2共线，则λ1λ2＝μ1μ2. ④若实数λ、μ使得λe 1＋μe 2＝0，则λ＝μ＝0. A ．①② B ．②③ C ．③④D ．②【跟踪训练】1 设e 1，e 2是不共线的两个向量，给出下列四组向量：①e 1与e 1＋e 2；②e 1－2e 2与e 2－2e 1；③e 1－2e 2与4e 2－2e 1；④e 1＋e 2与e 1－e 2. 其中，不能作为平面内所有向量的一组基底的是________(写出满足条件的序号)．题型二 用基底表示平面向量点拨：方法1：运用向量的线性运算法则对待求向量不断进行转化，直至用基底表示为止．方法2：通过列向量方程或方程组的形式，利用基底表示向量的唯一性求解． 例2 如图，已知在梯形ABCD 中，AD ∥BC ，E ，F 分别是AD ，BC 边上的中点，且BC ＝3AD ，BA →＝a ，BC →＝b .试以{a ，b }为基底表示EF →，DF →.【跟踪训练】2 如图所示，在△OAB 中，OA →＝a ，OB →＝b ，M 、N 分别是边OA 、OB 上的点，且OM →＝13a ，ON →＝12b ，设AN →与BM →交于点P ，用向量a 、b 表示OP →.分析: 通过列向量方程或方程组的形式，利用基底表示向量的唯一性求解λ1，λ2.【当堂达标】1.下列说法中，正确说法的个数是( ) ①在△ABC 中，AB →，AC →可以作为基底；②能够表示一个平面内所有向量的基底是唯一的； ③零向量不能作为基底．A ．0B ．1C ．2D ．32.如图在矩形ABCD 中，若BC →＝5e 1，DC →＝3e 2，则OC →＝( ) A.12(5e 1＋3e 2) B.12(5e 1－3e 2) C.12(3e 2－5e 1) D.12(5e 2－3e 1) 3.如图，在△OAB 中，P 为线段AB 上的一点，OP →＝xOA →＋yOB →，且BP→＝2PA →，则( )A ．x ＝23，y ＝13B ．x ＝13，y ＝23C ．x ＝14，y ＝34D ．x ＝34，y ＝144.已知非零向量OA →，OB →不共线，且2OP →＝xOA →＋yOB →，若PA →＝λAB →(λ∈R )，则x ，y 满足的关系是( )A ．x ＋y －2＝0B ．2x ＋y －1＝0C ．x ＋2y －2＝0D ．2x ＋y －2＝05.已知向量e 1，e 2不共线，实数x ，y 满足(3x －4y )e 1＋(2x －3y )e 2＝6e 1＋3e 2，则x －y＝ .6.如图，在平行四边形ABCD 中，设AC →＝a ，BD →＝b ，试用基底{a ，b }表示AB →，BC →.【参考答案】【自主学习】不共线向量 a ＝λ1e 1＋λ2e 2思考：基底中的两向量e 1，e 2不共线，这是基底的最大特点．平面内的基底并不是唯一的，任意不共线的两个向量都可以作为基底．【小试牛刀】(1) × (2)× (3)√ (4)√ (5) × (6)√ 【经典例题】例 1 B [解析] 由平面向量基本定理可知，①④是正确的．对于②，由平面向量基本定理可知，一旦一个平面的基底确定，那么任意一个向量在此基底下的实数对是唯一的．对于③，当λ1λ2＝0或μ1μ2＝0时不一定成立，应为λ1μ2－λ2μ1＝0.故选B ．【跟踪训练】1 ③ 解析：①设e 1＋e 2＝λe 1，则⎩⎪⎨⎪⎧λ＝1，1＝0，无解，所以e 1＋e 2与e 1不共线，即e 1与e 1＋e 2能作为一组基底．②设e 1－2e 2＝λ(e 2－2e 1)，则(1＋2λ)e 1－(2＋λ)e 2＝0，则⎩⎪⎨⎪⎧1＋2λ＝0，2＋λ＝0，无解，所以e 1－2e 2与e 2－2e 1不共线，即e 1－2e 2与e 2－2e 1能作为一组基底．③因为e 1－2e 2＝－12(4e 2－2e 1)，所以e 1－2e 2与4e 2－2e 1共线，即e 1－2e 2与4e 2－2e 1不能作为一组基底．④设e 1＋e 2＝λ(e 1－e 2)，则(1－λ)e 1＋(1＋λ)e 2＝0，则⎩⎪⎨⎪⎧1－λ＝0，1＋λ＝0，无解，所以e 1＋e 2与e 1－e 2不共线，即e 1＋e 2与e 1－e 2能作为一组基底．例2 解：连接FA ，DF .因为AD ∥BC ，且AD ＝13BC ，所以AD →＝13BC →＝13b ，所以AE →＝12AD →＝16b .因为BF →＝12BC →，所以BF →＝12b ，所以FA →＝BA →－BF →＝a －12b .所以EF →＝EA →＋AF →＝－AE →－FA →＝－16b －⎝⎛⎭⎪⎫a －12b ＝13b －a ，DF →＝DA →＋AF →＝－(AD →＋FA →)＝－⎣⎢⎡⎦⎥⎤13b ＋⎝ ⎛⎭⎪⎫a －12b ＝16b －a .【跟踪训练】2 [解] ∵OP →＝OM →＋MP →，OP →＝ON →＋NP →，设MP →＝mMB →，NP →＝nNA →，则OP →＝OM →＋mMB →＝13a ＋m (b －13a )＝13(1－m )a ＋m b ，OP →＝ON →＋nNA →＝12(1－n )b ＋n a .∵a 与b 不共线，∴⎩⎪⎨⎪⎧131－m ＝n ，121－n ＝m ，∴n ＝15.∴OP →＝15a ＋25b .【当堂达标】1.C 解析：①③正确，②错误．2.A 解析：选A.OC →＝12AC →＝12(BC →＋AB →)＝12(BC →＋DC →)＝12(5e 1＋3e 2)．3.A [解析] OP →＝OA →＋AP →＝OA →＋13AB →＝OA →＋13(OB →－OA →)＝23OA →＋13OB ．∴x ＝23，y ＝13.4.A 解析：选A.由PA →＝λAB →，得OA →－OP →＝λ(OB →－OA →)，即OP →＝(1＋λ)OA →－λOB →.又2OP→＝xOA →＋yOB →，所以⎩⎪⎨⎪⎧x ＝2＋2λ，y ＝－2λ，消去λ得x ＋y ＝2.5. 3 解析：∵e 1，e 2不共线，∴⎩⎪⎨⎪⎧3x －4y ＝62x －3y ＝3，解得⎩⎪⎨⎪⎧x ＝6y ＝3.∴x －y ＝3.6.解：法一：设AC ，BD 交于点O ，则有AO →＝OC →＝12AC →＝12a ，BO →＝OD →＝12BD →＝12b .所以AB →＝AO →＋OB →＝AO →－BO →＝12a －12b ，BC →＝BO →＋OC →＝12a ＋12b .法二：设AB →＝x ，BC →＝y ，则AD →＝BC →＝y ，又⎩⎪⎨⎪⎧AB →＋BC →＝AC →，AD →－AB →＝BD →，所以⎩⎪⎨⎪⎧x ＋y ＝a ，y －x ＝b ，解得x ＝12a －12b ，y ＝12a ＋12b ，即AB →＝12a －12b ，BC →＝12a ＋12b .《6.3.1平面向量的基本定理》同步练习A 组 基础题一、选择题1．等边△ABC 中，AB →与BC →的夹角是( ) A ．30° B．45° C．60° D．120°2．若e 1，e 2是平面内的一组基底，则下列四组向量能作为平面向量的基底的是( ) A ．e 1－e 2，e 2－e 1 B ．2e 1＋e 2，e 1＋12e 2C ．2e 2－3e 1,6e 1－4e 2D ．e 1＋e 2，e 1－e 23．下面三种说法中，正确的是( )①一个平面内只有一对不共线向量可作为表示该平面所有向量的基底；②一个平面内有无数多对不共线向量可作为该平面所有向量的基底；③零向量不可作为基底中的向量．A ．①② B．②③ C．①③ D．①②③4．若a 、b 不共线，且λa ＋μb ＝0(λ，μ∈R )，则( ) A ．a ＝0，b ＝0 B ．λ＝μ＝0 C ．λ＝0，b ＝0 D ．a ＝0，μ＝05.如图所示，平面内的两条直线OP 1和OP 2将平面分割成四个部分Ⅰ，Ⅱ，Ⅲ，Ⅳ(不包括边界)，若OP →＝aOP 1→＋bOP 2→，且点P 落在第Ⅰ部分，则实数a ，b 满足( )A ．a >0，b >0B ．a >0，b <0C ．a <0，b >0D ．a <0，b <06．下列说法中，正确说法的个数是( ) ①在△ABC 中，{AB →，AC →}可以作为基底；②能够表示一个平面内所有向量的基底是唯一的； ③零向量不能作为基底． A ．0 B ．1 C ．2 D ．37．如图，设O 是▱ABCD 两对角线的交点，有下列向量组：①AD →与AB →； ②DA →与BC →； ③CA →与DC →； ④OD →与OB →.其中可作为该平面内所有向量基底的是( ) A ．①② B ．①③ C ．①④ D ．③④8．M 为△ABC 的重心，点D ，E ，F 分别为三边BC ，AB ，AC 的中点，则MA →＋MB →＋MC →等于( ) A ．6ME → B ．－6MF → C ．0 D ．6MD →二、填空题9.设e 1、e 2是不共线的两个向量，给出下列四组向量：①e 1与e 1＋e 2；②e 1－2e 2与e 2－2e 1；③e 1－2e 2与4e 2－2e 1；④e 1＋e 2与e 1－e 2.其中能作为平面内所有向量的一组基底的序号是______．(写出所有满足条件的序号)10.如图，已知AB →＝a ，AC →＝b ，BD →＝3DC →，用a ，b 表示AD →，则AD →＝________.11．设向量m ＝2a －3b ，n ＝4a －2b ，p ＝3a ＋2b ，若用m ，n 表示p ，则p ＝________.12．在△ABC 中，AB →＝c ，AC →＝b .若点D 满足BD →＝2DC →，则AD →＝____________.(用b 、c 表示)13．已知向量e 1、e 2不共线，实数x 、y 满足(3x －4y )e 1＋(2x －3y )e 2＝6e 1＋3e 2，则x －y ＝3.14.如图，平面内有三个向量OA →、OB →、OC →.其中OA →与OB →的夹角为120°，OA →与OC →的夹角为30°，且|OA →|＝|OB →|＝1，|OC →|＝23，若OC →＝λOA →＋μOB →(λ，μ∈R )，则λ＋μ的值为________．15．设D ，E 分别是△ABC 的边AB ，BC 上的点，AD ＝12AB ，BE ＝23BC ，若DE →＝λ1AB →＋λ2AC→(λ1，λ2为实数)，则λ1＋λ2的值为________．三、解答题16.如图所示，在△ABC 中，点M 为AB 的中点，且AN ＝12NC ，BN 与CM 相交于点E ，设AB→＝a ，AC →＝b ，试以a ，b 为基底表示AE →.17.如图所示，在△ABC 中，点M 是BC 的中点，点N 在边AC 上，且AN ＝2NC ，AM 与BN 相交于点P ，求证：AP ∶PM ＝4∶1.18．在平行四边形ABCD 中，AB →＝a ，AD →＝b ，(1)如图1，如果E ，F 分别是BC ，DC 的中点，试用a ，b 分别表示BF →，DE →. (2)如图2，如果O 是AC 与BD 的交点，G 是DO 的中点，试用a ，b 表示AG →.B 组 能力提升一、选择题1.如图，在梯形ABCD 中，AB //CD ，AB ⊥AD ，AB ＝2AD ＝2DC ，E 是BC 的中点，F 是AE上一点，2，则（ ）A ．B ．C ．D ．2.在平行四边形ABCD 中，AC 与BD 交于点O ，E 是线段OD 的中点，AE 的延长线与CD 交于点F ，若，，则（ ）A ．B ．C ．D ．3.中，、分别是、上的点，且，，与交于点，则下列式子正确的是（ ）A ．B ．C ．D ． 4.如图，在直角梯形ABCD 中，AB =2AD =2DC ，E 为BC 边上一点，BC ⃗⃗⃗⃗⃗⃗⃗⃗ =3 EC ⃗⃗⃗⃗⃗⃗⃗ ，F 为AE 的中点，则BF ⃗⃗⃗⃗⃗⃗⃗⃗ =（ ）A ．13AB ⃗⃗⃗⃗⃗⃗⃗⃗ −23AD ⃗⃗⃗⃗⃗⃗⃗⃗ B ．−23AB ⃗⃗⃗⃗⃗⃗⃗⃗ +13AD ⃗⃗⃗⃗⃗⃗⃗⃗ C ．−13AB ⃗⃗⃗⃗⃗⃗⃗⃗ +23AD ⃗⃗⃗⃗⃗⃗⃗⃗D ．23AB ⃗⃗⃗⃗⃗⃗⃗⃗ −13AD ⃗⃗⃗⃗⃗⃗⃗⃗5.如图，正方形中，是的中点，若，则（ ）AF =FE BF=1123AB AD -1132AB AD -1123AB AD -+1132AB AD -+AC a =BD b =AF =1142a b +2133a b +1124a b +1233a b +ABC M N BC AC 2BM MC =2AN NC =AM BN P 3142AP AB AC =+1324AP AB AC =+1124AP AB AC =+1142AP AB AC =+ABCD M BC AC AM BD λμ=+λμ+=A ．B ．C ．D ．6.如图四边形ABCD 为平行四边形，，若，则的值为（ ）A ．B ．C ．D ．17.如图，在平行四边形中，为的中点，为的中点，若，则( )A ．B ．C ．D ．二、填空题8.如图，在中，，点在线段上移动（不含端点），若，则的取值范围是_____．4353158211,22AE AB DF FC ==AF AC DE λμ=+λμ-122313ABCD E BC FDE 34AF xAB AD =+x =34231214ABC 13B BCD →→=E AD AE AB AC λμ→→→=+12λμ+9.在中，D 为线段上一点，且，若，则.10.在中，为上一点，，为上任一点，若，则的最小值是 .三、解答题11.如图，△ABC 中，AD 为三角形BC 边上的中线且AE ＝2EC ，BE 交AD 于G ，求AG GD 及BGGE的值．《6.3.1平面向量的基本定理》同步练习答案解析A 组 基础题一、选择题1．等边△ABC 中，AB →与BC →的夹角是( ) A ．30° B．45° C．60° D．120° 答案 D2．若e 1，e 2是平面内的一组基底，则下列四组向量能作为平面向量的基底的是( ) A ．e 1－e 2，e 2－e 1 B ．2e 1＋e 2，e 1＋12e 2C ．2e 2－3e 1,6e 1－4e 2D ．e 1＋e 2，e 1－e 2ABC AB 3BD AD =CD CA CB λμ→→→=+λμ=ABC E AC 3AC AE =P BE (0,0)AP mAB nAC m n =+>>31m n+答案 D3．下面三种说法中，正确的是( )①一个平面内只有一对不共线向量可作为表示该平面所有向量的基底；②一个平面内有无数多对不共线向量可作为该平面所有向量的基底；③零向量不可作为基底中的向量．A ．①② B．②③ C．①③ D．①②③ 答案 B4．若a 、b 不共线，且λa ＋μb ＝0(λ，μ∈R )，则( ) A ．a ＝0，b ＝0 B ．λ＝μ＝0 C ．λ＝0，b ＝0 D ．a ＝0，μ＝0 答案 B5.如图所示，平面内的两条直线OP 1和OP 2将平面分割成四个部分Ⅰ，Ⅱ，Ⅲ，Ⅳ(不包括边界)，若OP →＝aOP 1→＋bOP 2→，且点P 落在第Ⅰ部分，则实数a ，b 满足( )A ．a >0，b >0B ．a >0，b <0C ．a <0，b >0D ．a <0，b <0 答案 C解析 当点P 落在第Ⅰ部分时，OP →按向量OP 1→与OP 2→分解时，一个与OP 1→反向，一个与OP 2→同向，故a <0，b >0.6．下列说法中，正确说法的个数是( ) ①在△ABC 中，{AB →，AC →}可以作为基底；②能够表示一个平面内所有向量的基底是唯一的； ③零向量不能作为基底． A ．0 B ．1 C ．2 D ．3 [答案] C解析：①③正确，②错误．7．如图，设O 是▱ABCD 两对角线的交点，有下列向量组：①AD →与AB →；②DA →与BC →；③CA →与DC →；④OD →与OB →.其中可作为该平面内所有向量基底的是( )A ．①②B ．①③C ．①④D ．③④ [答案] B解析：AD →与AB →不共线，DA →∥BC →，CA →与DC →不共线，OD →∥OB →，则①③可以作为该平面内所有向量的基底．8．M 为△ABC 的重心，点D ，E ，F 分别为三边BC ，AB ，AC 的中点，则MA →＋MB →＋MC →等于( ) A ．6ME → B ．－6MF → C ．0 D ．6MD → 答案 C解析 MA →＋MB →＋MC →＝MA →＋2MD →＝MA →＋AM →＝0. 二、填空题9.设e 1、e 2是不共线的两个向量，给出下列四组向量：①e 1与e 1＋e 2；②e 1－2e 2与e 2－2e 1；③e 1－2e 2与4e 2－2e 1；④e 1＋e 2与e 1－e 2.其中能作为平面内所有向量的一组基底的序号是______．(写出所有满足条件的序号)答案 ①②④解析 对于③4e 2－2e 1＝－2e 1＋4e 2＝－2(e 1－2e 2)，∴e 1－2e 2与4e 2－2e 1共线，不能作为基底．10.如图，已知AB →＝a ，AC →＝b ，BD →＝3DC →，用a ，b 表示AD →，则AD →＝________.答案 14a ＋34b解析 AD →＝AB →＋BD →＝AB →＋34BC →＝AB →＋34(AC →－AB →)＝14AB →＋34AC →＝14a ＋34b . 11．设向量m ＝2a －3b ，n ＝4a －2b ，p ＝3a ＋2b ，若用m ，n 表示p ，则p ＝________. 答案 －74m ＋138n解析 设p ＝x m ＋y n ，则3a ＋2b ＝x (2a －3b )＋y (4a －2b )＝(2x ＋4y )a ＋(－3x －2y )b ，得⎩⎪⎨⎪⎧2x ＋4y ＝3－3x －2y ＝2⇒⎩⎪⎨⎪⎧x ＝－74，y ＝138.12．在△ABC 中，AB →＝c ，AC →＝b .若点D 满足BD →＝2DC →，则AD →＝____________.(用b 、c 表示)答案 23b ＋13c解析 AD →＝AB →＋BD →＝AB →＋23BC →＝AB →＋23(AC →－AB →)＝13AB →＋23AC →＝23b ＋13c .13．已知向量e 1、e 2不共线，实数x 、y 满足(3x －4y )e 1＋(2x －3y )e 2＝6e 1＋3e 2，则x －y ＝3.[答案] 3解析：∵e 1、e 2不共线，∴⎩⎪⎨⎪⎧3x －4y ＝6，2x －3y ＝3，解得⎩⎪⎨⎪⎧x ＝6，y ＝3，∴x －y ＝3.14.如图，平面内有三个向量OA →、OB →、OC →.其中OA →与OB →的夹角为120°，OA →与OC →的夹角为30°，且|OA →|＝|OB →|＝1，|OC →|＝23，若OC →＝λOA →＋μOB →(λ，μ∈R )，则λ＋μ的值为________．答案 6解析 如图，以OA 、OB 所在射线为邻边，OC 为对角线作平行四边形ODCE ，则OC →＝OD →＋OE →.在Rt△OCD 中，∵|OC →|＝23， ∠COD ＝30°，∠OCD ＝90°， ∴|OD →|＝4，|CD →|＝2，故OD →＝4OA →， OE →＝2OB →，即λ＝4，μ＝2，∴λ＋μ＝6.15．设D ，E 分别是△ABC 的边AB ，BC 上的点，AD ＝12AB ，BE ＝23BC ，若DE →＝λ1AB →＋λ2AC→(λ1，λ2为实数)，则λ1＋λ2的值为________．答案 12解析 易知DE →＝12AB →＋23BC →＝12AB →＋23(AC →－AB →)＝－16AB →＋23AC →.所以λ1＋λ2＝12.三、解答题16.如图所示，在△ABC 中，点M 为AB 的中点，且AN ＝12NC ，BN 与CM 相交于点E ，设AB→＝a ，AC →＝b ，试以a ，b 为基底表示AE →.解 ∵AN →＝13AC →＝13b ，AM →＝12AB →＝12a ，由N ，E ，B 三点共线知存在实数λ满足AE →＝λAN →＋(1－λ)AB →＝13λb ＋(1－λ)a .由C ，E ，M 三点共线知存在实数μ满足 AE →＝μAM →＋(1－μ)AC →＝μ2a ＋(1－μ)b .∴⎩⎪⎨⎪⎧1－λ＝μ2，1－μ＝λ3，解得⎩⎪⎨⎪⎧λ＝35，μ＝45.∴AE →＝25a ＋15b .17.如图所示，在△ABC 中，点M 是BC 的中点，点N 在边AC 上，且AN ＝2NC ，AM 与BN 相交于点P ，求证：AP ∶PM ＝4∶1. 证明 设AB →＝b ，AC →＝c ， 则AM →＝12b ＋12c ，AN →＝23AC →，BN →＝BA →＋AN →＝23c －b .∵AP →∥AM →，BP →∥BN →，∴存在λ，μ∈R ，使得AP →＝λAM →，BP →＝μBN →， 又∵AP →＋PB →＝AB →，∴λAM →－μBN →＝AB →，∴由λ⎝ ⎛⎭⎪⎫12b ＋12c －μ⎝ ⎛⎭⎪⎫23c －b ＝b 得 ⎝ ⎛⎭⎪⎫12λ＋μb ＋⎝ ⎛⎭⎪⎫12λ－23μc ＝b .又∵b 与c 不共线． ∴⎩⎪⎨⎪⎧12λ＋μ＝1，12λ－23μ＝0.解得⎩⎪⎨⎪⎧λ＝45，μ＝35.故AP →＝45AM →，即AP ∶PM ＝4∶1.18．在平行四边形ABCD 中，AB →＝a ，AD →＝b ，(1)如图1，如果E ，F 分别是BC ，DC 的中点，试用a ，b 分别表示BF →，DE →. (2)如图2，如果O 是AC 与BD 的交点，G 是DO 的中点，试用a ，b 表示AG →. 解 (1)BF →＝BC →＋CF →＝AD →＋12CD →＝AD →－12AB →＝－12a ＋b .DE →＝DC →＋CE →＝AB →－12AD →＝a －12b .(2)BD →＝AD →－AB →＝b －a ，∵O 是BD 的中点，G 是DO 的中点，∴BG →＝34BD →＝34(b －a )，∴AG →＝AB →＋BG →＝a ＋34(b －a )＝14a ＋34b .B 组 能力提升一、选择题1.如图，在梯形ABCD 中，AB //CD ，AB ⊥AD ，AB ＝2AD ＝2DC ，E 是BC 的中点，F 是AE 上一点，2，则（ ）A ．B ．C ．D ． 【答案】C【解析】由梯形ABCD 中，AB CD ，AB ⊥AD ，AB ＝2AD ＝2DC ，E 是BC 的中点，F 是AE 上一点，2，则 ；故选：C2.在平行四边形ABCD 中，AC 与BD 交于点O ，E 是线段OD 的中点，AE 的延长线与CD 交于点F ，若，，则（ ）A ．B ．C ．D ． 【答案】B【解析】如图，可知AF =FE BF=1123AB AD -1132AB AD -1123AB AD -+1132AB AD -+//AF =FE 221(332)BF BA AF AB AE AB AB AC =+=-+=-+⨯+1(3)AB AB AD DC =-+++11(32)AB AB AD AB =-+++1123AB AD =-+AC a =BD b =AF =1142a b +2133a b +1124a b +1233a b +=，选B. 3.中，、分别是、上的点，且，，与交于点，则下列式子正确的是（ ）A ．B ．C ．D ． 【答案】D【解析】如下图所示：连接，则，，，， 因此，.故选：D. 4.如图，在直角梯形ABCD 中，AB =2AD =2DC ，E 为BC 边上一点，BC ⃗⃗⃗⃗⃗⃗⃗⃗ =3 EC ⃗⃗⃗⃗⃗⃗⃗ ，F 为AE 的中点，则BF ⃗⃗⃗⃗⃗⃗⃗⃗ =（ ）222()333AF AC CF AC CD AC AB AC AO OB =+=+=-=-+2112112132232233AC AC BD a a b a b ⎛⎫⎛⎫--=--=+ ⎪ ⎪⎝⎭⎝⎭ABC M N BC AC 2BM MC =2AN NC =AM BN P 3142AP AB AC =+1324AP AB AC =+1124AP AB AC =+1142AP AB AC =+MN 12NC MC AN BM ==//MN AB ∴PMN PAB △∽△13PM MN AP BC ∴==()333231444342AP AM AB BM AB BC AB BC ⎛⎫==+=+=+ ⎪⎝⎭()31114242AB AC AB AB AC =+-=+A ．13AB ⃗⃗⃗⃗⃗⃗⃗⃗ −23AD ⃗⃗⃗⃗⃗⃗⃗⃗ B ．−23AB ⃗⃗⃗⃗⃗⃗⃗⃗ +13AD ⃗⃗⃗⃗⃗⃗⃗⃗ C ．−13AB ⃗⃗⃗⃗⃗⃗⃗⃗ +23AD ⃗⃗⃗⃗⃗⃗⃗⃗ D ．23AB ⃗⃗⃗⃗⃗⃗⃗⃗ −13AD ⃗⃗⃗⃗⃗⃗⃗⃗【答案】B【解析】由图可知：BF →=12BA →+12BE →，BE →=23BC →，BC →=AC →﹣AB →，AC →=AD →+DC →，DC →=12AB →，∴BF →=﹣12AB →+13（AD →+12AB →﹣AB →）=﹣23AB →+13AD →，故选B ．5.如图，正方形中，是的中点，若，则（ ）A ．B ．C ．D ．【答案】B【解析】以为坐标原点建立平面直角坐标系，设正方形边长为， 由此，，故， 解得.故选B. 6.如图四边形ABCD 为平行四边形，，若，则的值为（ ）ABCD M BC AC AM BD λμ=+λμ+=43531582A 1()()11,1,1,,1,12AC AM BD ⎛⎫===- ⎪⎝⎭11,12λμλμ=-=+415,,333λμλμ==+=11,22AE AB DF FC ==AF AC DE λμ=+λμ-A ．B ．C ．D ．1【答案】D【解析】选取为基底， 则， 又，将以上两式比较系数可得．故选D ．7.如图，在平行四边形中，为的中点，为的中点，若，则( )A ．B ．C ．D ．【答案】C【解析】因为为的中点，所以， 而， 即有，又，所以．122313,AB AD 13AF AD DF AB AD =+=+()()122AF AC DE AB AD AB AD AB AD μλμλμλλμ⎛⎫⎛⎫=+=+++-=++- ⎪ ⎪⎝⎭⎝⎭1λμ-=ABCD E BC F DE 34AF xAB AD =+x =34231214F DE ()12AF AD AE =+1122AE AB BE AB BC AB AD =+=+=+11132224AF AD AB AD AB AD ⎛⎫=++=+ ⎪⎝⎭34AF xAB AD =+12x =故选：C ．二、填空题8.如图，在中，，点在线段上移动（不含端点），若，则的取值范围是_____．【答案】 【解析】由题可知，，设，则，所以， 而，可得：，所以，设， 由双钩函数性质可知，在上单调递减，则， 所以的取值范围是.故答案为：. 9.在中，D 为线段上一点，且，若，则. 【答案】3 【解析】，ABC 13B BCD →→=E AD AE AB AC λμ→→→=+12λμ+(10,3)+∞13B BCD →→=()01AE mAD m =<<13AE m AB BC ⎛⎫=+ ⎪⎝⎭()13m AB BA AC ⎡⎤=++⎢⎥⎣⎦2133AE m AB m AC →→→=+AE AB AC λμ→→→=+21,33m m λμ==1323m m λμ+=+()01m <<()33m f x m=+()01m <<()f x ()0,1()()1101333f x f >=+=12λμ+(10,3)+∞(10,3)+∞ABC AB 3BD AD =CD CA CB λμ→→→=+λμ=3BD AD =3331()4444CD CB BD CB BA CB CA CB CA CB →→→→→→→→→→∴=+=+=+-=+又，，，故选：310.在中，为上一点，，为上任一点，若，则的最小值是 . 【答案】12【解析】由题意可知：，三点共线，则：，据此有：， 当且仅当时等号成立. 综上可得：的最小值是12.三、解答题11.如图，△ABC 中，AD 为三角形BC 边上的中线且AE ＝2EC ，BE 交AD 于G ，求AG GD 及BGGE的值．解 设AG GD ＝λ，BG GE＝μ. ∵BD →＝DC →，即AD →－AB →＝AC →－AD →， ∴AD →＝12(AB →＋AC →)．又∵AG →＝λGD →＝λ(AD →－AG →)，∴AG →＝λ1＋λAD →＝λ2(1＋λ)AB →＋λ2(1＋λ)AC →.又∵BG →＝μGE →，即AG →－AB →＝μ(AE →－AG →)， ∴(1＋μ)AG →＝AB →＋μAE →，AG →＝11＋μAB →＋μ1＋μAE →.又AE →＝23AC →，∴AG →＝11＋μAB →＋2μ3(1＋μ)AC →.∵AB →，AC →不共线，CD CA CB λμ→→→=+31,44λμ∴==3λμ∴=ABC E AC 3AC AE =P BE (0,0)AP mAB nAC m n =+>>31m n+3AP mAB nAC mAB nAE =+=+,,A B E 31m n +=()313199366212n m n m m n m n m n m n m n⎛⎫+=++=++≥+⨯= ⎪⎝⎭11,26m n ==31m n+∴⎩⎪⎨⎪⎧λ2(1＋λ)＝11＋μ，λ2(1＋λ)＝2μ3(1＋μ).解之，得⎩⎪⎨⎪⎧λ＝4，μ＝32.∴AG GD ＝4，BG GE ＝32.《6.3.1平面向量基本定理》同步检测试卷一、基础巩固1．下列各组向量中，可以作为基底的是（ ）． A ．， B ．， C ．，D ．， 2．在中，，则等于（ ） A ．B ．C ．D ．3．如图所示，，分别是的边，上的点，且，，则向量（ ）．A ．B ．C ．D ．4．已知平面直角坐标系内的两个向量,且平面内的任一向()10,0e =()21,2e =-()11,2e =-()25,7e =()13,5e =()26,10e =()12,3e =-213,24e ⎛⎫=-⎪⎝⎭ABC AB a =CB b =CA a b +a b -b a -a b --M N ABCAB AC 2AM MB =2NC AN =MN =1233AB AC -1233AB AC +1233AC AB -1233AC AB +(3,2),(1,2)a m b m =-=-量都可以唯一表示成(为实数),则实数m 的取值范围是( )A ．B ．C ．D ．5．中所在的平面上的点满足，则（ ） A ． B ． C ． D ． 6．设，是不共线的两个向量，且，则（ ） A ．B ．C ．D ．7．如图，在平行四边形中，为的中点，为的中点，若，则( )A ．B ．C ．D ．8在中，已知是延长线上一点，若，点为线段的中点，，则（ ）A ．B ．C ．D ．9．（多选）下列各组向量中，不能作为基底的是（ ）c c a b λμ=+,λμ6,5⎛⎫+∞ ⎪⎝⎭66,,55⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭(,2)-∞(,2)(2,)-∞-⋃-+∞ABC ∆D 2BD DC =AD =3144AD AB AC =+1344AD AB AC =+2133AD AB AC =+1233AD AB AC =+a b 0,,a b R λμλμ+=∈0λμ==0ab 0,0b λ==0,0a μ==ABCD E BC F DE 34AF xAB AD =+x =34231214ABC D BC2BCCD =E AD AE AB AC λμ=+2λμ+=14-1412-12A ．，B ．，C ．，D ．，10.（多选）已知M 为△ABC 的重心，D 为BC 的中点，则下列等式成立的是（ ） A ． B ． C ． D ． 11．（多选）如果是平面α内两个不共线的向量，那么下列说法中不正确的是（ ） A ．(λ，μ∈R )可以表示平面α内的所有向量B ．对于平面α内任一向量，使的实数对(λ，μ)有无穷多个C ．若向量与共线，则有且只有一个实数λ，使得D ．若实数λ，μ使得，则λ=μ=012．（多选）已知正方形的边长为，向量，满足，，则（ ）A ．B ．C ．D ．二、拓展提升13．如图，设，，又，试用，表示．14．如图，在任意四边形ABCD 中，()10,0e =()21,1=e ()11,2e =()22,1e =-()13,4e =-234,55⎛⎫=-⎪⎝⎭e ()12,6=e ()21,3=--e MA MB MC ==0MA MB MC ++=1233CM CA CD =+2133BM BA BD =+12,e e 12e e λμ+a 12a e e λμ=+1112e e λμ+2122e e λμ+()11122122e e e e λμλλμ+=+120e e λμ+=ABCD 2a b 2AB a =2AD a b =+||22b =a b ⊥2a b(4)a b b +⊥OA a =OB b =43AP AB =a b OP（1）已知E ､F 分别是AD ､BC 的中点求证：. （2）已知，用，表示向量. 15．已知点G 是的重心,M 是边的中点.若过的重心G ,且,求证:. 答案解析 一、基础巩固1．下列各组向量中，可以作为基底的是（ ）． A ．， B ．， C ．， D ．， 【答案】B 【详解】因为与不共线，其余选项中、均共线，所以B 选项中的两向量可以作为基底．2．在中，，则等于（ ） A ． B ．C ．D ．【答案】C 【详解】2AB DC EF +=12AM MB =EA EB EM ABO ∆AB PQ ABO ∆,,,OA a OB b OP ma OQ nb ====113m n+=()10,0e =()21,2e =-()11,2e =-()25,7e =()13,5e =()26,10e =()12,3e =-213,24e ⎛⎫=-⎪⎝⎭()11,2e =-()25,7e =1e 2e ABC AB a =CB b =CA a b +a b -b a -a b --，3．如图所示，，分别是的边，上的点，且，，则向量（ ）．A ．B ．C ．D ．【答案】C 【详解】因为，， 所以. 4．已知平面直角坐标系内的两个向量,且平面内的任一向量都可以唯一表示成(为实数),则实数m 的取值范围是( )A ．B ．C ．D ．【答案】B 【详解】由题意可知,平面内的任一向量都可以唯一表示成, ∴是平面内表示所有向量的一个基底,. ∴不共线, ∴. CA CB BA b AB b a =+=-=-M N ABC AB AC 2AM MB =2NC AN =MN=1233AB AC -1233AB AC +1233AC AB -1233AC AB +2AM MB =2NC AN =1233MN AN AM AC AB =-=-(3,2),(1,2)a m b m =-=-c c a b λμ=+,λμ6,5⎛⎫+∞ ⎪⎝⎭66,,55⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭(,2)-∞(,2)(2,)-∞-⋃-+∞c c a b λμ=+,a b ,a b 3(2)20m m -+≠65m ≠故m 的取值范围是.5．中所在的平面上的点满足，则（ ） A ． B ． C ． D ． 【答案】D 【详解】解：因为， 所以，所以， 6．设，是不共线的两个向量，且，则（ ） A ． B ． C ． D ．【答案】A 【详解】因为，是不共线的两个向量,所以由平面向量基本定理知：若，则， 7．如图，在平行四边形中，为的中点，为的中点，若，则( )A ．B ．C ．D ．【答案】C 【详解】66,,55⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭ABC ∆D 2BD DC =AD =3144AD AB AC =+1344AD AB AC =+2133AD AB AC =+1233AD AB AC =+2BD DC =()2AD AB AC AD -=-1233AD AB AC =+a b 0,,a b R λμλμ+=∈0λμ==0ab 0,0b λ==0,0a μ==a b 0,,a b R λμλμ+=∈0λμ==ABCD E BC F DE 34AF xAB AD =+x =34231214因为为的中点，所以， 而， 即有，又，所以． 8．在中，已知是延长线上一点，若，点为线段的中点，，则（ ）A ．B ．C ．D ．【答案】B 【详解】 解：由题意可得，，故， ∴.9．（多选）下列各组向量中，不能作为基底的是（ ） A ．， B ．，C ．，D ．，【答案】ACD 【详解】F DE ()12AF AD AE =+1122AE AB BE AB BC AB AD =+=+=+11132224AF AD AB AD AB AD ⎛⎫=++=+ ⎪⎝⎭34AF xAB AD =+12x =ABC D BC 2BC CD =E AD AE AB AC λμ=+2λμ+=14-1412-12111111131()()222222444AE AD AC CD AC BC AC AC AB AC AB ==+=+⨯=+-=-13,44λμ=-=241λμ+=()10,0e =()21,1=e ()11,2e =()22,1e =-()13,4e =-234,55⎛⎫=- ⎪⎝⎭e ()12,6=e ()21,3=--eA ，C ，D 中向量与共线，不能作为基底；B 中，不共线，所以可作为一组基底．10．（多选）已知M 为△ABC 的重心，D 为BC 的中点，则下列等式成立的是（ ） A ． B ． C ． D ． 【答案】BC 【详解】M 为△ABC 的重心，M 是三边中线的交点，且在中线三等分点处，对于A ，由于△ABC 为任意三角形，故中线不一定相等，则不一定相等，故A 错误；对于B ，D 为BC 的中点，，，，故B 正确；对于C ，，故C 正确；对于D ，，故D 错误.11．（多选）如果是平面α内两个不共线的向量，那么下列说法中不正确的是（ ） A ．(λ，μ∈R )可以表示平面α内的所有向量B ．对于平面α内任一向量，使的实数对(λ，μ)有无穷多个1e 2e 1e 2e MA MB MC ==0MA MB MC ++=1233CM CA CD =+2133BM BA BD =+∴,,MA MB MC 2MB M MD C +∴=2MA MD =-0MA MB MC ++=∴()22123333CM CA AM CA AD CA CD CA CA CD =+=+=+-=+()22123333BM BA BA BA B AM AD BD BA A BD +=+=+-==+12,e e 12e e λμ+a 12a e e λμ=+C ．若向量与共线，则有且只有一个实数λ，使得D ．若实数λ，μ使得，则λ=μ=0 【答案】BC 【详解】由平面向量基本定理可知，A ，D 是正确的.对于B ，由平面向量基本定理可知， 若一个平面的基底确定，则该平面内的任意一个向量在此基底下的实数对是唯一的，B 错误.对于C ，当两个向量均为零向量时，即λ1=λ2=μ1=μ2=0时，这样的λ有无数个，或当为非零向量，而为零向量(λ2=μ2=0)，此时λ不存在. 12．（多选）已知正方形的边长为，向量，满足，，则（ ）A ．B ．C ．D ．【答案】AD 【详解】由条件可，所以，A 正确；，与不垂直，B 错误； ，C 错误；，根据正方形的性质有，所以，D正确.二、拓展提升13．如图，设，，又，试用，表示．【答案】. 1112e e λμ+2122e e λμ+()11122122e e e e λμλλμ+=+120e e λμ+=1112e e λμ+2122e e λμ+ABCD 2ab 2AB a =2AD a b =+||22b =a b ⊥2a b(4)a b b +⊥b AD AB BD =-=||||22b BD ==12a AB =BD 122a b AB BD ⋅=⋅=-4a b AB AD AC +=+=AC BD ⊥(4)a b b +⊥OA a =OB b =43AP AB =a b OP 1433OP a b =-+【详解】 解：，由已知可得：，所以， 故．14．如图，在任意四边形ABCD 中，（1）已知E ､F 分别是AD ､BC 的中点求证：.（2）已知，用，表示向量. 【答案】（1）证明见解析；（2）.【详解】（1）证明：因为E ､F 分别是AD ､BC 的中点，所以，， 由题意，，两式相加得， 即；（2）因为，所以， 所以.15．已知点G 是的重心,M 是边的中点.若过的重心G ,且,求证:. AP OP OA =-AB OB OA =-43AP AB =4()3OP OA OB OA -=-44143333OP OA OA OB a b =-+=-+1433OP a b =-+2AB DC EF +=12AM MB =EA EB EM 1233EM EB EA =+0ED EA +=0CF BF +=EF ED DC CF =++EF EA AB BF =++2EF ED DC CF EA AB BF =+++++AB DC =+2AB DC EF +=12AM MB =13AM AB =()11123333EM EA AM EA AB EA EB EA EB EA =+=+=+-=+ABO ∆AB PQ ABO ∆,,,OA a OB b OP ma OQ nb ====113m n+=【答案】见解析 【详解】因为M 是边的中点,所以. 因为G 是的重心,所以.由P ,G ,Q 三点共线,所以有且只有一个实数,使，，，又因为不共线， ，消去，整理得,故.AB 11()()22OM OA OB a b =+=+ABO ∆21()33OG OM a b ==+λPG PQ λ=,(1)OG OP OQ OP OG OQ OP λλλλ-=-=+-,OP ma OQ nb ==(1))1(3OG nb a a b m λλ=+-=+,a b 1=313n m m λλ⎧⎪⎪⎨⎪-=⎪⎩λ3mn m n =+113m n+=。

《数据的表示》教案一、教学目标：知识与技能：1. 理解数据的概念和意义；2. 掌握数据的收集、整理和表示方法；3. 学会使用图表来表示数据，并能进行简单的数据分析。

过程与方法：1. 培养学生的观察能力、思考能力和动手操作能力；2. 学会与他人合作交流，培养团队精神。

情感态度价值观：1. 培养学生的数据意识，感受数据与生活的密切联系；2. 培养学生对数据的兴趣和好奇心，激发学生学习数据的积极性。

二、教学内容：1. 数据的收集与整理数据的概念和意义数据的收集方法数据的整理方法2. 数据的表示方法表格表示法图片表示法图表表示法3. 柱状图和条形图柱状图的定义和特点条形图的定义和特点柱状图和条形图的绘制方法4. 折线图折线图的定义和特点折线图的绘制方法折线图的应用实例5. 饼图饼图的定义和特点饼图的绘制方法饼图的应用实例三、教学重点与难点：重点：1. 数据的收集、整理和表示方法；2. 柱状图、条形图、折线图和饼图的绘制方法和应用。

难点：1. 数据的整理方法；2. 柱状图、条形图、折线图和饼图的绘制方法和应用。

四、教学方法：采用讲授法、示范法、实践法、讨论法、案例分析法等多种教学方法，引导学生主动参与，提高学生的学习兴趣和积极性。

五、教学准备：教师准备：1. 教学PPT；2. 教学案例和数据；3. 柱状图、条形图、折线图和饼图的模板；4. 学生分组合作的材料和工具。

学生准备：1. 课本和相关学习材料；2. 笔记本和笔；3. 积极参与课堂讨论和实践活动。

六、教学过程：1. 导入：通过生活中的实例，引导学生了解数据的概念和意义，激发学生对数据的兴趣和好奇心。

2. 数据的收集与整理：讲解数据的收集方法，如问卷调查、观察等，以及数据的整理方法，如分类、排序等。

3. 数据的表示方法：介绍表格表示法、图片表示法和图表表示法，并通过实例展示各种表示法的应用。

4. 柱状图和条形图：讲解柱状图和条形图的定义和特点，示范绘制方法，并让学生进行实践操作。

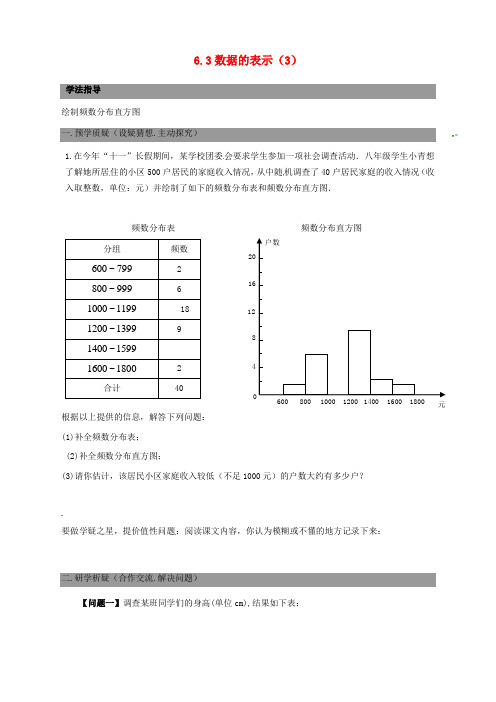
6.3数据的表示（3）学法指导绘制频数分布直方图一.预学质疑（设疑猜想.主动探究）。

1.在今年“十一”长假期间，某学校团委会要求学生参加一项社会调查活动．八年级学生小青想了解她所居住的小区500户居民的家庭收入情况，从中随机调查了40户居民家庭的收入情况（收入取整数，单位：元）并绘制了如下的频数分布表和频数分布直方图．根据以上提供的信息，解答下列问题： (1)补全频数分布表； (2)补全频数分布直方图；(3)请你估计，该居民小区家庭收入较低（不足1000元）的户数大约有多少户？要做学疑之星，提价值性问题：阅读课文内容，你认为模糊或不懂的地方记录下来：二.研学析疑（合作交流.解决问题）【问题一】调查某班同学们的身高(单位cm),结果如下表：元频数分布表频数分布直方图将数据用适当的统计图表表示出来步骤：1.计算极差:这组数据的最小数是:141cm,最大的数是:172cm,它们的差(极差)是:________________2.定组距,分组:根据极差分组(经验法则：100个数据以内分5－12组);3.统计每组数据出现的次数4.绘制频数分布表：三.导法展示(巩固升华.拓展思维)1.某中学部分同学参加全国初中数学竞赛，取得了优异的成绩，指导老师统计了所有参赛同学的成绩（成绩都是整数，试题满分120分），并且绘制了“频数分布直方图”（如图）．请回答：（1）该中学参加本次数学竞赛的有多少名同学？（2）如果成绩在90分以上（含90分）的同学获奖，那么该中学参赛同学的获奖率是多少？四.促评反思（反思评价.课外练习）1.2008年11月28日，为扩大内需，国务院决定在全国实施“家电下乡”政策．第一批列入家电下乡的产品为彩电.冰箱.洗衣机和手机四种产品．某县一家家电商场，今年一季度对以上四种产品的销售情况进行了统计，绘制了如下的统计图，请你根据图中信息解答下列问题： （1）该商场一季度彩电销售的数量是 台． （2）请补全条形统计图和扇形统计图．2.某单位对全体职工的年龄进行了调查统计，结果如下（单位：岁）：将数据适当分组，列出频数分布表，绘制相应的频数分布直方图．解：最大值是______,最小值是______,极差是________,岁；取组距为10岁，可以分成_________组小结：绘制频数分布直方图的一般步骤有：（1）计算最大值与最小值的差（极差），确定统计量的范围； （2）决定组数和组距；（3）确定分点；（4）列频数分布表；（5）画频数分布直方图。

第三节 数据的表示【学习目标】1、理解扇形统计图的特点，并能从中获取有用信息；2、会运用圆和扇形的总体与部分的关系制作扇形统计图；3、了解频数概念及意义；4、了解频数分布的意义，会绘制频数直方图。

【学习重难点】重点：扇形统计图和条形统计图的特点、制作、应用及频数的概念。

难点：频数的表示方法。

【学习过程】 模块一 预习反馈 一．自主学习（P165—173）1.扇形统计图：利用圆和扇形来表示 的关系，这样的统计图叫做扇形统计图。

2. 绘制扇形统计图的步骤（五步）:（1）计算各部分的 ；（2）计算各部分 的度数（关键步骤）；（3）画圆、画 ；（4）标出 ；（5）写名称.3.小强是校学生会体育部部长，他想了解现在同学们更喜欢什么球类运动，以便学生会组织受同学们欢迎的比赛.于是他设计了调查问卷，在全校每个班随机选取了10名同学进行调查，调查结果如下：模块二 合作探究1．你喜欢足球吗？下面是对某校七年级学生的调查结果：(1)计算两种看法的男同学人数占全体男生人数的百分比和所在扇形圆心角的度数并填表中;(2)画出各个扇形，并写出名称、标出百分比．2.王大爷开了一个报亭，为了使每天进的某种报纸适量 ，王大爷对这种报纸40天的销售情况作了调查，这40 天卖出这种报纸的份数如下：136，175，153，135，161，140，155，180，179， 166，188，142，144，154，155，157，160，162， 135，156，148，173，154，145，158，150，154，168，168，155，169，157，157，149，134，167，151，144，155，131.将上面数据适当分组，作出频数直方图，说明王大爷每天进多少这种报纸比较合适？解：（1）列频数分布表： （2）画频数直方图，如图所示.模块三 小结反思讲一下你本节课学习了哪些新知识？用到了什么方法或数学思想？知识：制作扇形统计图，了解频数分布的意义，会绘制频数直方图。

6.3数据的表示（2）学法指导留意课本中重要例题，能说出条形统计图的概念和特点；并能利用表格整理数据，作出条形统计图一.预学质疑（设疑猜想.主动探究）书籍是人类进步的阶梯，同学们在课外最爱读那一类书籍？文学类（A）.漫画类（B）.科普类（C）.历史类（D）下面是小亮调查的七（1）班50位同学喜欢的书籍，结果如下:A ABCD A B A A C B A A C B C A A B C A A B A CD A A C D B A C D A A A C D A C B A A C C D A A C根据上面结果，请用“正”字统计出喜欢各类书籍的人数，根据统计的结果你能得到哪些结论？要做学疑之星，提价值性问题：阅读课文内容，你认为模糊或不懂的地方记录下来：二.研学析疑（合作交流.解决问题）【问题一】课本P168的表格是某校初一（2）班的同学入学信息表：（1）你能用恰当的统计图表表示该班同学入学时的英语成绩吗？（2）从你的图表中能看出大部分同学处于哪个等级？成绩的整体分布情况怎样？【问题二】你能用恰当的统计图表表示该班同学入学时的语文成绩吗？从你的图表中能看出大部分同学处于哪个分数段？成绩的整体分布情况怎样？小组内试着用图表和条形统计图合作完成，完成后组内交流.你能借鉴英语成绩的表示，将语文成绩按10分的距离分段，统计每个分数段的学生数：再将上表在下面绘制成条形统计图：绘制完成后与课本对照，你有什么新的发现？三.导法展示(巩固升华.拓展思维)1.初中生的视力状况受到社会的广泛关注，某市有关部门对全市3万名初中生的视力状况进行了一次抽样调查，下图是利用所得数据绘制的频数分布直方图，根据图中所提供的信息回答下列问题：(1)本次调查共抽测了多少名学生？(2)如果视力在4.9-5.1（含4.9和5.1）均属正常，那么全市有多少名初中生视力正常？四、小结反思（自主整理，归纳总结）五、促评反思（反思评价、课外练习）1.从某市中学参加初中毕业考试的学生成绩中抽取40名学生的数学成绩，分数如下：90，86，61，86，73，86，91，68，75，65，72，81，86，99，79，80，86，74，83，77，86，93，96，88，87，86，92，77，98，94，100，86，64，100，69，90，95，97，84，94.(1) 将数据进行整理，填入下表 (2)根据表格中的数据绘制频数分布直方图4.5-69.59.5-94.5。

第三节 数据的表示【学习目标】1、理解扇形统计图的特点，并能从中获取有用信息；2、会运用圆和扇形的总体与部分的关系制作扇形统计图；3、了解频数概念及意义；4、了解频数分布的意义，会绘制频数直方图。

【学习重难点】重点：扇形统计图和条形统计图的特点、制作、应用及频数的概念。

难点：频数的表示方法。

【学习过程】 模块一 预习反馈一．自主学习（P165—173）1.扇形统计图：利用圆和扇形来表示 的关系，这样的统计图叫做扇形统计图。

2. 绘制扇形统计图的步骤（五步）:（1）计算各部分的 ；（2）计算各部分 的度数（关键步骤）；（3）画圆、画 ；（4）标出 ；（5）写名称.3.小强是校学生会体育部部长，他想了解现在同学们更喜欢什么球类运动，以便学生会组织受同学们欢迎的比赛.于是他设计了调查问卷，在全校每个班随机选取了10名同学进行调查，调查结果如下：你最喜欢的球类运动是（ ） （单选）A 篮球B 足球C 排球D 兵乓球E 羽毛球F 其他球类运模块二 合作探究1．你喜欢足球吗？下面是对某校七年级学生的调查结果：(1)计算两种看法的男同学人数占全体男生人数的百分比和所在扇形圆心角的度数并填表中;(2)画出各个扇形，并写出名称、标出百分比．2.王大爷开了一个报亭，为了使每天进的某种报纸适量 ，王大爷对这种报纸40天的销售情况作了调查，这40 天卖出这种报纸的份数如下：136，175，153，135，161，140，155，180，179， 166，188，142，144，154，155，157，160，162， 135，156，148，173，154，145，158，150，154，168，168，155，169，157，157，149，134，167，151，144，155，131.将上面数据适当分组，作出频数直方图，说明王大爷每天进多少这种报纸比较合适？解：（1）列频数分布表： （2）画频数直方图，如图所示. 最喜欢的球类运动 篮球足球排球乒乓球 羽毛球其他得票数 69632796369百分比 圆心角 喜欢的 不喜欢的 合计 人数(人) 75 25 百分比 圆心角份数(x)划记频数 130≤x ＜140 正5140≤x＜150150≤x＜160正正正15160≤x＜170170≤x＜180180≤x＜190合计模块三小结反思讲一下你本节课学习了哪些新知识？用到了什么方法或数学思想？知识：制作扇形统计图，了解频数分布的意义，会绘制频数直方图。

七年级上 6.3数据的表示（1） 导学案学习目标：理解扇形统计图的特点，会制作扇形统计图，并能从中获取信息； 一、课前导学1.扇形统计图是利用圆和_______表示______和部分的关系,圆代表的是总体, 即100%,扇形代表______,圆的大小与总数量无关.2.扇形统计图能清楚地表示出各部分在总体中所占的_______.3.如图1,如果用整个图表示总体,那么_______扇形表示总体的13,______ 扇形表示总体的12_______.(1)C A B300亩油菜500亩小麦450亩大麦(2)A 65%B 28%(3)C60以下20%91~10025%60~7525%76~9030%(4)4.红星村今年对农田秋季播种作物如图2规划,且只种植这三种农作物,则该村种植的大麦占种植所有农作物的____%.5.光明中学对图书馆的书分成3类,A 表示科技类,B 表示科学类,C 表示艺术类,所占的百分比如图3所示,如果该校共有图书8500册,则艺术书共有______册. 二、课堂练习6.某校对初一300名学生数学考试作一次调查,在某范围内的得分率如图4的扇形,则在60分以下这一分数线中的人数为( ) A.75 B.60 C.90 D.507.某公司有员工700人,元旦举行活动,图5,A 、B 、C 分别表示参加各种活动的人数的百分比,规定每人只参加一项且每人均参加,则不下围棋的人共有( )A.259人B.441人C.350人D.490人C打扑克B下围棋37%A下象棋(5)8.某校男、女生比例如图6中的扇形区,则男生占全校人数的百分数 为( ) A.48% B.52% C.92.3% D.4%三、能力拓展9.全班约25是男生,约35是女生,请画出扇形统计图.10.(1)由图中提供信息:乒乓球、排球、足球、篮球4项球类活动中, 哪一类球类运动能够获得全班近14的支持率?(2)若全班人数为50人,体育委员组织一次排球比赛, 估计会有多少人积极参加比赛?蓝球16%排球18%足球24%其它乒乓球32%11.一所中学准备搬迁到新校舍,在迁校舍之前就该校300名学生如何到校舍进行了一次调查,,能得到什么结论? 说说你的理由.自我评价 小组评价 老师评价。