河北大学2012年校内数学建模竞赛、选拔试题
- 格式:pdf
- 大小:811.53 KB
- 文档页数:3

一、问题重述确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。
请尝试建立数学模型讨论下列问题:1. 分析附件1中两组评酒员的评价结果有无显著性差异,哪一组结果更可信?2. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。
3. 分析酿酒葡萄与葡萄酒的理化指标之间的联系。
4.分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量?二、问题分析2.1 对问题一的分析该评酒员分为第一组和第二组两组,其中每组有10人分别对红葡萄酒和白葡萄酒进行品尝,并对各酒样品的外观、香气、口感和平衡/整体各方面进行评分。
由于每个品酒员自己本身上的差异,存在着主观误差,为避免评酒员主观上的误差,本文去掉最高分和一个最低分,然后再计算出各组品酒员对各样品酒的平均分。
这样得到的数据更具准确性。
2.2 对问题二的分析根据附件二酿酒葡萄的理化指标和葡萄酒的质量利用之成分分析,选用酿酒葡萄的一级指标,对多次测试的,我们取其平均值。
利用matlab软件实现其主成分分析,具体程序可见附录一。
最后,可到各个酿酒葡萄的排名和得分情况,再取一些分数值就可以对酿酒葡萄进行分类了。
2.3对问题三分析在问题二中对酿酒葡萄进行了分类,我们选用一级酿酒葡萄和葡萄酒来进行相关性分析。
由于酿酒葡萄和葡萄酒的理化指标过多,所以我们选用一级指标进行分析。
又根据文献3对酿酒葡萄选用VC含量、多酚氧化酶活力、总酚、总糖、还原糖、可溶性固形物、固酸比来进行分析。
利用spss软件进行相关性分析,得到酿酒葡萄和葡萄酒的相关性表,分析总结就可得到它们之间的联系。
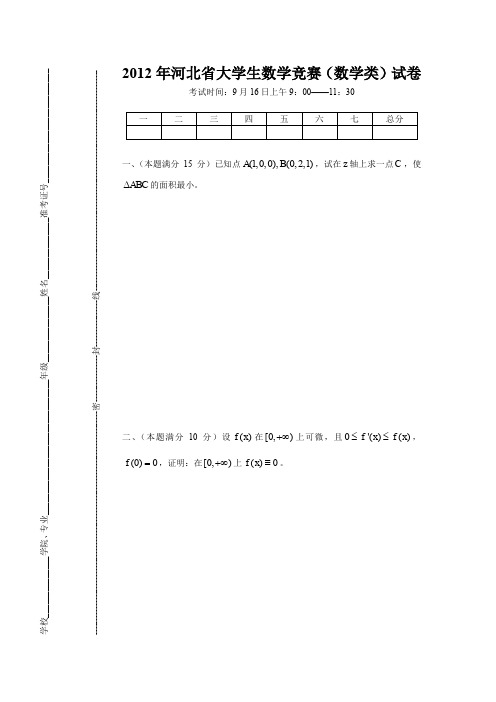
2012年河北省大学生数学竞赛(数学类)试卷考试时间:9月16日上午9:00——11:30一、(本题满分15分)已知点(1,0,0),(0,2,1)A B ,试在z 轴上求一点C ,使ABC ∆的面积最小。
二、(本题满分10分)设()f x 在[0,)+∞上可微,且0'()()f x f x ≤≤,(0)0f =,证明:在[0,)+∞上()0f x ≡。
学校______________学院、专业_______________________________年级_______________姓名______________准考证号__________________________ -----------------------------------------------------------------------------密----------------封----------------线----------------------------------------------------------------------------三、(本题满分10分)设()f x 在[],a b 上具二阶导数,()()0f a f b ==,且存在(,)c a b ∈使得()0f c >。
证明存在(,)a b ξ∈使得''()0f ξ<。
四、(本题满分15分)设1(2),0,1,2,...n n n x x x n +=-=,试确定初值0x ,使得数列{}n x 收敛。
学校______________学院、专业_______________________________年级_______________姓名______________准考证号__________________________ -----------------------------------------------------------------------------密----------------封----------------线----------------------------------------------------------------------------五、(本题满分15分)设()x ϕ,()f x 是(,)-∞+∞上的连续函数,且存在0R >,当||x R ≥时()0x ϕ=。

2012高教社杯全国大学生数学建模竞赛题目
佚名
【期刊名称】《数学建模及其应用》
【年(卷),期】2012(001)004
【摘要】A题:葡萄酒的评价确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。
请尝试建立数学模型讨论下列问题:
【总页数】2页(P55-56)
【正文语种】中文
【相关文献】
1.雨量预报方法的模糊评价模型--2005高教社杯全国大学生数学建模竞赛题目之
一 [J], 杨金山;耿玉菊;马小女
2.2016年“高教社杯”全国大学生数学建模竞赛题目 [J],
3.NBA赛程的分析和评价——2008高教社杯全国大学生数学建模竞赛题目 [J], 马明远
4.2012高教社杯全国大学生数学建模竞赛题目 [J], ;
5.2016年“高教社杯”全国大学生数学建模竞赛题目 [J],
因版权原因,仅展示原文概要,查看原文内容请购买。

描述统计量均值标准差分析 N 天门冬氨酸75.6341 20.68785 27 苏氨酸152.9496 80.05794 27 丝氨酸124.6556 56.67784 27 谷氨酸117.0330 63.52041 27 脯氨酸1441.5378 1557.60578 27 甘氨酸79.5337 52.14485 27 丙氨酸55.2167 29.02871 27 胱氨酸24.2585 12.99296 27 缬氨酸28.8896 11.63951 27 蛋氨酸8.2985 4.98859 27 异亮氨酸17.5300 11.85535 27 亮氨酸24.9378 13.34513 27 酪氨酸 3.4504 2.19987 27 苯丙氨酸 4.7326 2.71900 27 赖氨酸33.0193 19.53507 27 组氨酸23.2141 13.00215 27描述统计量均值标准差分析 N 天门冬氨酸75.6341 20.68785 27 苏氨酸152.9496 80.05794 27 丝氨酸124.6556 56.67784 27 谷氨酸117.0330 63.52041 27 脯氨酸1441.5378 1557.60578 27 甘氨酸79.5337 52.14485 27 丙氨酸55.2167 29.02871 27 胱氨酸24.2585 12.99296 27 缬氨酸28.8896 11.63951 27 蛋氨酸8.2985 4.98859 27 异亮氨酸17.5300 11.85535 27 亮氨酸24.9378 13.34513 27 酪氨酸 3.4504 2.19987 27 苯丙氨酸 4.7326 2.71900 27 赖氨酸33.0193 19.53507 27 组氨酸23.2141 13.00215 27 精氨酸141.5248 106.81323 27成份矩阵a成份1 2 3 4 5天门冬氨酸.512 .504 .386 .279 .180 苏氨酸.374 .639 -.355 -.205 .343 丝氨酸.746 .103 -.103 .415 -.117 谷氨酸.690 .562 -.139 -.220 -.025 脯氨酸-.104 .034 -.187 .739 .532 甘氨酸.482 .676 .068 -.101 -.238 丙氨酸.622 .449 -.185 -.039 -.068 胱氨酸.392 .168 .051 .603 -.475 缬氨酸.861 -.237 .040 .025 -.161 蛋氨酸.703 .043 -.233 -.270 .408 异亮氨酸.756 -.170 .252 -.131 -.180 亮氨酸.853 -.286 .152 -.038 -.081 酪氨酸.317 -.119 .763 -.144 .218 苯丙氨酸.187 .093 .669 .046 .318 赖氨酸.693 -.466 -.198 .224 .194 组氨酸.796 -.525 -.158 -.073 .078 精氨酸.635 -.508 -.226 -.114 .023 提取方法 :主成份。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期: 2012 年 9 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):太阳能小屋设计模型摘要太阳能利用的重点是建筑,其应用方式包括利用太阳能为建筑物供热(生活热水、采暖)和供电,因此太阳能与建筑一体化是未来太阳能技术的发展方向。
本文首先通过对其合理性进行了定量的分析、概率知识,结合房屋建筑学,地理学。
对附件4的数据进行初始筛选,在计算出电池板价格的基础上,将适合每种电池版的有效辐射强度进行年度求和,以此判别出各个墙面的铺设方案。
问题一,根据约束条件对目标函数收益最大进行建模并使用lingo 软件进行求解,考虑到逆变器的价格,额定电流以及输入电压范围,选择合适的电池组,得到35年的投入产出比为 2.00743394091.99188883.3=,回收年限为P K N /==8.67年。

2012年数学建模考试题题目1:学习数学建模课程的感悟!答:数学模型(Mathematical Model)是一种模拟,是用数学符号、数学式子、程序、图形等对实际课题本质属性的抽象而又简洁的刻划,它或能解释某些客观现象,或能预测未来的发展规律,或能为控制某一现象的发展提供某种意义下的最优策略或较好策略。
数学模型一般并非现实问题的直接翻版,它的建立常常既需要人们对现实问题深入细微的观察和分析,又需要人们灵活巧妙地利用各种数学知识。
这种应用知识从实际课题中抽象、提炼出数学模型的过程就称为数学建模(Mathematical Modeling)。
数学建模应当掌握的几类算法:1、数据拟合、参数估计、插值等数据处理算法(比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用Matlab作为工具)2、线性规划、整数规划、多元规划、二次规划等规划类问题(建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo 软件实现)3、动态规划、回溯搜索、分治算法、分支定界等计算机算法(这些算法是算法设计中比较常用的方法,很多场合可以用到竞赛中)4、网格算法和穷举法(网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具)5、一些连续离散化方法(很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的)9.数值分析算法(如果在比赛中采用高级语言进行编程的话,那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就----------------------------精品word文档值得下载值得拥有----------------------------------------------需要额外编写库函数进行调用)题目2:1题:某高校后勤集团运营绩效分析根据高等教育体制改革和全国高校后勤社会化改革精神,高校后勤集团在各高校相继成立。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): a我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):葡萄酒的评价摘要本文利用SPSS和MATLAB软件对葡萄酒评价问题进行了分析,综合采用了t检验、主成分分析、聚类分析和灰色关联度分析等方法,建立了数学模型,并设计了一套对葡萄酒质量的评价体系。
关于问题一:首先,对两组评酒员对同一种葡萄酒给出的评分结果进行处理;其次,采用t检验判断出两组评分结果存在显著性差异;最后,利用每一组评酒员对同一种葡萄酒的评分方差作为衡量依据,建立评分机制,评估两个小组所给结果的可信性,经分析第一组、第二组得分分别为13分、42分。
因此,第二组评酒员的评分结果更可信。
关于问题二:首先,对酿酒葡萄的理化指标进行主成分分析,挖掘出若干个影响酿酒葡萄理化指标的主要成分;其次,根据第一问的结果,将第二组评酒员的评分作为衡量葡萄酒质量的量化指标;最后,通过聚类分析将酿酒葡萄分为4个等级。
2012高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题葡萄酒的评价确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。
请尝试建立数学模型讨论下列问题:1. 分析附件1中两组评酒员的评价结果有无显著性差异,哪一组结果更可信?2. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。
3. 分析酿酒葡萄与葡萄酒的理化指标之间的联系。
4.分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量?附件1:葡萄酒品尝评分表(含4个表格)附件2:葡萄和葡萄酒的理化指标(含2个表格)附件3:葡萄和葡萄酒的芳香物质(含4个表格)答案仅供参考:1. 分析附件1中两组评酒员的评价结果有无显著性差异根据表1计算的各取样点葡萄质量综合评分结果, 结合当地气象资料,进行相关普查和回归分析, 挑选出相关性显著, 并通过0. 01显著性检验的11个因子, 果实着色期平均最低气温(Tn45 )、果实着色期平均日较差(D45 )、果实着色期平均相对湿度(U45 )、果实着色期降水量(R 45 )、果实着色期水热系数(K 45 )、全生育期平均相对湿度(Ug )、全生育期降水量(Rg )、全生育期水热系数(Kg )、7~ 8月份降水量(R 7- 8 )、日照时数( S7- 8 )、水热系数(K 7- 8 )。
利用DPS3. 01 数据处理系统对这些影响因素进行因子分析, 并进行倾斜旋转( promaxrotation)得到11种影响酿酒葡萄品质气象因子结构如表5。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):2.3.指导教师或指导教师组负责人(打印并签名):指导教师组日期:2012 年9 月10 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国评阅编号(由全国组委会评阅前进行编号):太阳能小屋的设计摘要本文针对太阳能小屋设计问题,根据题目中附件所给的数据,结合实际情况,建立了天空各向同性模型,利用目标优化思想,分析了光伏电池的不同安装方式时,小屋外表面光伏电池的优化铺设方案。
并计算出了小屋光伏电池35年寿命期内的发电总量、经济效益及投资的回收年限。
针对问题一,建立天空各向同性模型,算出了大同市太阳能小屋一年中各个面的太阳能辐照量,仅考虑贴附安装方式,从电池的性能、价格、转换率、寿命等方面设计出了小屋外表面光伏电池的铺设方案,从而给出小屋各外表面光伏电池的优化方案。
并且计算出小屋光伏电池35年寿命期内的发电总量为777846度,净收入为109697元,投资的回收年限为21年。
针对问题二,由太阳辐射能公式可以计算出山西大同地区的电池板最佳倾角为34度,在问题一的基础上,得到了架空方式安装光伏电池时,小屋各外表面光伏电池的优化方案。
并可以计算出小屋光伏电池35年寿命期内的发电总量为943177度,净收入为192362元,投资的回收年限为20年。