简单迭代法与加速方法实验报告
- 格式:doc
- 大小:131.00 KB
- 文档页数:8


第1篇一、实验目的1. 理解雅各比迭代法的原理和应用。
2. 掌握雅各比迭代法的计算步骤和实现方法。
3. 通过实验验证雅各比迭代法在求解线性方程组中的有效性和收敛性。
二、实验原理雅各比迭代法是一种求解线性方程组的迭代方法。
对于形如Ax=b的线性方程组,其中A是n×n的系数矩阵,x是n维未知向量,b是n维常数向量,雅各比迭代法的基本思想是将方程组Ax=b转化为一系列的简单方程进行迭代求解。
设A为对角占优矩阵,则雅各比迭代法的迭代公式为:x_{k+1} = (D - L)^{-1}(b - Ux_k)其中,D是A的对角矩阵,L是A的非对角元素中下三角矩阵,U是A的非对角元素中上三角矩阵。
三、实验内容1. 准备实验环境:安装MATLAB软件,创建实验文件夹。
2. 编写实验程序:(1)定义系数矩阵A和常数向量b。
(2)计算对角矩阵D、下三角矩阵L和上三角矩阵U。
(3)初始化迭代变量x_0。
(4)设置迭代次数N和容许误差ε。
(5)进行雅各比迭代计算,并输出每一步的迭代结果。
(6)判断迭代是否收敛,若收敛则输出最终结果,否则输出未收敛信息。
3. 运行实验程序,观察迭代过程和结果。
四、实验步骤1. 创建实验文件夹,打开MATLAB软件。
2. 编写实验程序,保存为“雅各比迭代法实验.m”。
3. 运行实验程序,观察迭代过程和结果。
4. 分析实验结果,验证雅各比迭代法的有效性和收敛性。
五、实验结果与分析1. 运行实验程序,得到以下迭代过程和结果:迭代次数 | 迭代结果---------|---------1 | x_1 = [0.3333, 0.3333]2 | x_2 = [0.3333, 0.3333]3 | x_3 = [0.3333, 0.3333]...N | x_N = [0.3333, 0.3333]2. 分析实验结果:(1)从实验结果可以看出,雅各比迭代法在求解线性方程组时,经过有限次迭代即可收敛。

实验一线性方程组迭代法实验实验一线性方程组迭代法实验一、实验目的1.掌握用迭代法求解线性方程组的基本思想和计算步骤;2.能熟练地写出Jacobi迭代法的迭代格式的分量形式,并能比较它们各自的特点及误差估计;3.理解迭代法的基本原理及特点,并掌握Jacobi迭代Gauss-Seidel迭代和SOR迭代格式的分量形式、矩阵形式及其各自的特点;4.掌握Jacobi迭代Gauss-Seidel迭代和SOR 迭代算法的MATLAB程序实现方法,及了解松弛因子对SOR迭代的影响;5.用SOR迭代法求解线性方程组时,超松弛因子ω的取值大小会对方程组的解造成影响,目的就是能够探索超松弛因子ω怎样对解造成影响,通过这个实验我们可以了解ω的大致取值范围。
二、实验题目1、迭代法的收敛速度用迭代法分别对n=20,n=200解方程组Ax=b,其中n n A ⨯ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫------------------=444...444315131315151313151513131515131315131 (1)选取不同的初值x0和不同的右端向量b ,给定迭代误差,用两种迭代法计算,观测得到的迭代向量并分析计算结果给出结论;(2)取定初值x0和右端向量b ,给定迭代误差,将A 的主对角元成倍放大,其余元素不变,用Jacobi 迭代法计算多次,比较收敛速度,分析计算结果并给出结论。
2、SOR 迭代法松弛因子的选取不同的松弛因子对解得影响。
然后利用雅可比迭代求的的解与它们比较;三、 实验原理1、迭代法的收敛速度运用了Jacobi 迭代,Gauss-Seidel 迭代1)Jacobi 迭代算法:1. 取初始点x(0),精度要求ε,最大迭代次数N ,置k :=0;2. 由n 1i ),x a -(b x n i j 1,j (k)j j i i 11)(k i ,,⋯==∑≠=+ii a ,计算出x (k+1);3. 若ε≤-∞+)()1(k k x x ,则停算,输出x(k+1)作为方程组的近似解; 4. 若k=N ,则停算,输出迭代失败信息;否则置k :=k+1,转步2。
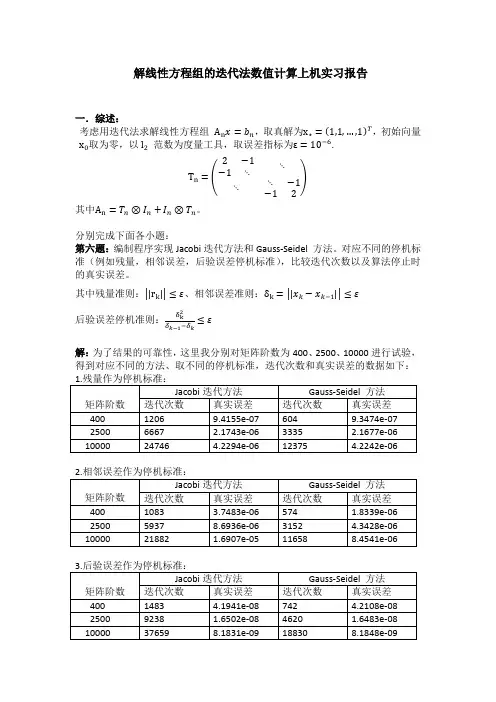
解线性方程组的迭代法数值计算上机实习报告一.综述:考虑用迭代法求解线性方程组,取真解为,初始向量取为零,以范数为度量工具,取误差指标为.其中。
分别完成下面各小题:第六题:编制程序实现Jacobi迭代方法和Gauss-Seidel 方法。
对应不同的停机标准(例如残量,相邻误差,后验误差停机标准),比较迭代次数以及算法停止时的真实误差。
其中残量准则:、相邻误差准则:后验误差停机准则:解:为了结果的可靠性,这里我分别对矩阵阶数为400、2500、10000进行试验,得到对应不同的方法、取不同的停机标准,迭代次数和真实误差的数据如下:分析上面数据可知,对应不同的停机标准,GS方法的迭代次数都近似为J方法的一半,这与理论分析一致。
而且从迭代次数可以看出,在这个例子中,作为停机标准,最强的依次为后验误差,再到残量,再到相邻误差。
第七题:编写程序实现SOR 迭代方法。
以真实误差作为停机标准,数值观测SOR 迭代方法中松弛因子对迭代次数的影响,找到最佳迭代因子的取值。
解:本题中考虑n=50,即对2500阶的矩阵A。
由于我们已经知道要使SOR方法收敛,松弛因子需要位于。
下面来求SOR方法中对应的最佳松弛因子。
应用筛选法的思想,第一次我们取松弛因子,间距为0.05,得到的对应的图像如下,从图中可以看出迭代次数随着的增大,先减小后变大,这与理论相符。
同时可以看出最佳松弛因子.第二次将区间细分为10份,即取,可得下面第二幅图像,从图像中可以看出最佳松弛因子第八题:对于J 方法,GS方法和(带有最佳松弛因子的)SOR 方法,分别绘制误差下降曲线以及残量的下降曲线(采用对数坐标系),绘制(按真实误差)迭代次数与矩阵阶数倒数的关系;解:对于J方法,考虑n=50时,采用相邻误差为迭代的终止条件,误差下降曲线及残量的下降曲线如下:对于GS方法,考虑n=50的时候,采用相邻误差作为迭代的终止条件,所得到的残量和误差的下降曲线如下图:从中可以看出,当相邻误差满足误差指标时,真实误差却并不小于误差指标,而为2.6281e-04。

实验五线性方程组的迭代法实验一. 实验目的(1)深入理解线性方程组的迭代法的设计思想,学会利用系数矩阵的性质以保证迭代过程的收敛性,以及解决某些实际的线性方程组求解问题。
(2)熟悉Matlab编程环境,利用Matlab解决具体的方程求根问题。
二. 实验要求建立Jacobi迭代公式、Gauss-Seidel迭代公式和超松弛迭代公式,用Matlab软件实现线性方程组求解的Jacobi迭代法、Gauss-Seidel迭代法和超松弛迭代法,并用实例在计算机上计算。
三. 实验内容1. 实验题目(1)分别利用Jacobi迭代和Gauss-Seidel迭代求解下列线性方程组,取x0={0 ,0,0,0,0-,o}t (2)分别取w=1、1.05、1.1、1.25和 1.8,用超松弛法求解上面的方程组,要求精度为510。
2. 设计思想1.Jacobi迭代: Jacobi迭代的设计思想是将所给线性方程组逐步对角化,将一般形式的线性方程组的求解归结为对角方程组求解过程的重复。
2.Gauss-Seidel迭代: Gauss-Seidel迭代的设计思想是将一般形式的线性方程组的求解过程归结为下三角方程组求解过程的重复。
3.超松弛迭代:基于Gauss-Seidel迭代,对i=1,2,…反复执行计算迭代公式,即为超松弛迭代。
3. 对应程序1.Jacobi迭代:function [x,k]=Jacobimethod(A,b,x0,N,emg)%A是线性方程组的左端矩阵,b是右端向量,x0是迭代初始值% N表示迭代次数上限,emg表示控制精度,k表示迭代次数,x是解n=length(A);x1=zeros(n,1);x2=zeros(n,1);x1=x0;k=0;r=max(abs(b-A*x1));while r>emgfor i=1:nsum=0;for j=1:nif i~=jsum=sum+A(i,j)*x1(j);endendx2(i)=(b(i)-sum)/A(i,i);endr=max(abs(x2-x1));x1=x2;k=k+1;if k>Ndisp('迭代失败,返回');return;endendx=x1;2.Gauss-Seidel迭代:function [x,k]=Gaussmethod(A,b,x0,N,emg)%A是线性方程组的左端矩阵,b是右端向量,x0是迭代初始值% N表示迭代次数上限,emg表示控制精度,k表示迭代次数,x是解n=length(A);x1=zeros(n,1);x2=zeros(n,1);x1=x0;r=max(abs(b-A*x1));k=0;while r>emgfor i=1:nsum=0;for j=1:nif j>isum=sum+A(i,j)*x1(j);elseif j<isum=sum+A(i,j)*x2(j);endendx2(i)=(b(i)-sum)/A(i,i);endr=max(abs(x2-x1));x1=x2;k=k+1;if k>Ndisp('迭代失败,返回');return;endendx=x1;3.超松弛(SOR)迭代:function [x,k]=SORmethod(A,b,x0,N,emg,w)%A是线性方程组的左端矩阵,b是右端向量,x0是迭代初始值% N表示迭代次数上限,emg表示控制精度,k表示迭代次数,x是解%w表示松弛因子n=length(A);x1=zeros(n,1);x2=zeros(n,1);x1=x0;r=max(abs(b-A*x1));k=0;while r>emgfor i=1:nsum=0;for j=1:nif j>=isum=sum+A(i,j)*x1(j);elseif j<isum=sum+A(i,j)*x2(j);endendx2(i)=x1(i)+w*(b(i)-sum)/A(i,i); endr=max(abs(x2-x1)); x1=x2; k=k+1; if k>Ndisp('迭代失败,返回'); return; end end x=x1;四. 实验体会 在同等精度下,Gauss-Seidel 迭代法比Jacobi 迭代法收敛速度快。


MAAB计算方法迭代法牛顿法二分法实验报告实验目的:比较MAAB计算方法中迭代法、牛顿法和二分法的优缺点,探究它们在求解方程中的应用效果。
实验原理:1、迭代法:将方程转化为x=f(x)的形式,通过不断迭代逼近方程的根。
2、牛顿法:利用函数在特定点的切线逼近根的位置,通过不断迭代找到方程的根。
3、二分法:利用函数值在区间两端的异号性质,通过不断二分缩小区间,最终逼近方程的根。
实验步骤:1、选择一元方程进行求解,并根据方程选择不同的计算方法。
2、在迭代法中,根据给定的初始值和迭代公式,进行迭代计算,直到满足预设的迭代精度要求。
3、在牛顿法中,选择初始点,并根据切线方程进行迭代计算,直到满足预设的迭代精度要求。
4、在二分法中,选择区间,并根据函数值的异号性质进行二分,直到满足预设的迭代精度要求。
5、根据计算结果,比较三种方法的求解效果,包括迭代次数、计算时间、求解精度等指标。
实验结果与分析:通过对多个方程进行测试,得到了以下实验结果:1、迭代法的优点是简单易懂,适用范围广,但当迭代公式不收敛时会导致计算结果不准确。
2、牛顿法的优点是收敛速度较快,但需要计算函数的一阶导数和二阶导数,对于复杂函数较难求解。
3、二分法的优点是收敛性较好,不需要导数信息,但收敛速度较慢。
4、对于线性方程和非线性方程的求解,牛顿法和迭代法通常比二分法更快速收敛。
5、对于多重根的方程,二分法没有明显优势,而牛顿法和迭代法能更好地逼近根的位置。
6、在不同的方程和初值选择下,三种方法的迭代次数和求解精度略有差异。
7、在时间效率方面,二分法在收敛速度较慢的同时,迭代次数较少,牛顿法在收敛速度较快的同时,迭代次数较多,而迭代法对于不同方程有较好的平衡。
结论:1、对于不同类型的方程求解,可以根据具体情况选择合适的计算方法。
2、迭代法、牛顿法和二分法各有优缺点,没有绝对的最优方法,需要权衡各种因素选择最适合的方法。
3、在实际应用中,可以根据方程的特点和精度要求综合考虑不同方法的优劣势,以获得较好的求解效果。

(完整word版)迭代法解线性方程组-数值分析实验报告编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整word版)迭代法解线性方程组-数值分析实验报告)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整word版)迭代法解线性方程组-数值分析实验报告的全部内容。
数学与计算科学学院《数值分析》课程设计题目:迭代法解线性方程组专业:信息与计算科学学号: 1309302—24姓名:谭孜指导教师:郭兵成绩:二零一六年六月二十日一、前言:(目的和意义)1.实验目的①掌握用迭代法求解线性方程组的基本思想和步骤.②了解雅可比迭代法,高斯—赛德尔法和松弛法在求解方程组过程中的优缺点。
2。
实验意义迭代法是用某种极限过程去逐步逼近线性方程组精确解的方法,它是解高阶稀疏方程组的重要方法。
迭代法的基本思想是用逐次逼近的方法求解线性方程组。
比较雅可比迭代法,高斯—赛德尔迭代方法和松弛法,举例子说明每种方法的试用范围和优缺点并进行比较.二、数学原理:设有方程组b Ax = …① 将其转化为等价的,便于迭代的形式f Bx x += …② (这种转化总能实现,如令b f A I B =-=,), 并由此构造迭代公式f Bx x k k +=+)()1( …③ 式中B 称为迭代矩阵,f 称为迭代向量。
对任意的初始向量)0(x ,由式③可求得向量序列∞0)(}{k x ,若*)(lim x x k k =∞→,则*x 就是方程①或方程②的解。
此时迭代公式②是收敛的,否则称为发散的。
构造的迭代公式③是否收敛,取决于迭代矩阵B 的性 1。
雅可比迭代法基本原理设有方程组),,3,2,1(1n i b x a j j nj ij ==∑= …①矩阵形式为b Ax =,设系数矩阵A 为非奇异矩阵,且),,3,2,1(,0n i a ii =≠从式①中第i 个方程中解出x,得其等价形式)(111j nj j ij ii i x a b a x ∑≠=-= …②取初始向量),,,()0()0(2)0(1)0(n x x x x =,对式②应用迭代法,可建立相应的迭代公式: )(111)()1(∑≠=++-=nj j i k j ij ii k ib x a a x…③ 也可记为矩阵形式:J x J k F B x k +==)()1( …④ 若将系数矩阵A 分解为A=D —L-U ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=--=--00000000000000111211212211212222111211n n n nn n nn nn n n n n a a a a a a a a a a a a a a a a a a U L D A式中⎪⎪⎪⎪⎪⎭⎫⎝⎛=nn a a a D2211,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-0000121323121nn n n a a a a a a L ,⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=-0000122311312n n n n a a a a a a U 。

6.5迭代法的加速一、教学目标及基本要求通过对本节的学习,使学生掌握方程求根迭代法的加速。
二、教学内容及学时分配本章主要介绍线性方程求根的迭代法的加速方法。
要求1.了解数值分析的研究对象、掌握误差及有关概念。
2.正确理解使用数值方法求方程的解的基本思想、数学原理、算法设计。
3.了解插值是数值逼近的重要方法之一,正确理解每一种算法的基本思想、计算公式、算法设计、程序框图设计和源程序。
4.掌握数值积分的数学原理和程序设计方法。
5.能够使用数值方法解决一阶常微分方程的初值问题。
6.理解和掌握使用数值方法对线性方程组求解的算法设计。
三、教学重点难点1.教学重点:非线性方程迭代收敛性与迭代加速、牛顿法。
2.教学难点:迭代的收敛性。
四、教学中应注意的问题多媒体课堂教学为主。
适当提问,加深学生对概念的理解,迭代加速的算法实现。
五、教案正文6.1 迭代公式的加工迭代过程收敛缓慢,计算量将很大,需要进行加速。
设 x k是根x*的某个近似值,用迭代公式校正一次得x k 1x k,假设' ( x)在所考察得范围内变化不大,其估计值为L ,则有:x *xk 1L( x * x k )x * 1 L xk 1L x k1 1 L有迭代公式 x k 11 x k 1Lx k ,是比 x k 1 更好的近似根。
这样加工后1 L1 L的计算过程为:迭代 x k 1 x k改进 x k 11L x kx k 11L1 L合并的 x k 11 [ ( x k )Lx k ]1 L例 3 P1336.2 埃特金算法上述加速方法含有导数'x ,不便于计算。
设将迭代值 x k 1x k 再迭代~x k 1 ,由于 x *~L ( x *x k1)一次,又得 x k 1xk 1又 x * x k 1L( x *x k ) ,消去 L 得x * xk 1x *x k~ ~x k 1 ) 2x *( x k 1*~x *xk 1xk 1~2x k 1x kx x k 1xk 1计算过程如下:迭代 x k1x k~1xk 1迭代 x k~~1x k 1 ) 2改进 x k( x k1x k1~2x k 1 x kx k 1小结:这节课我们主要介绍了线性方程组迭代法加速的基本思想及其常用的几种迭代方法。
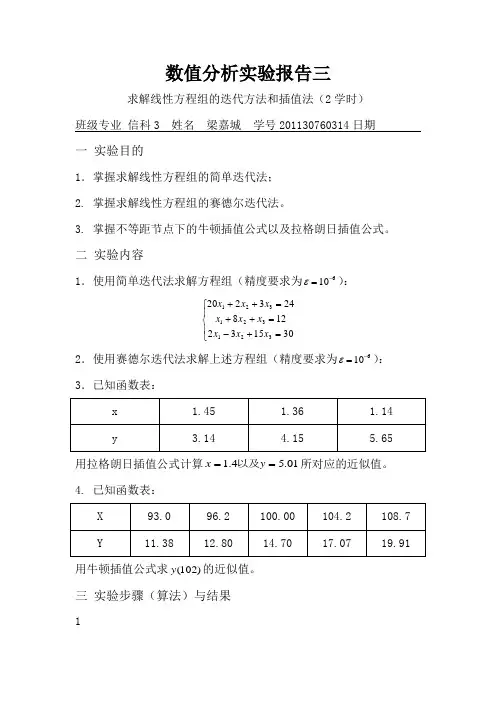
数值分析实验报告三求解线性方程组的迭代方法和插值法(2学时)班级专业 信科3 姓名 梁嘉城 学号201130760314日期一 实验目的1.掌握求解线性方程组的简单迭代法; 2. 掌握求解线性方程组的赛德尔迭代法。
3. 掌握不等距节点下的牛顿插值公式以及拉格朗日插值公式。
二 实验内容1.使用简单迭代法求解方程组(精度要求为610-=ε):⎪⎩⎪⎨⎧=+-=++=++301532128243220321321321x x x x x x x x x 2.使用赛德尔迭代法求解上述方程组(精度要求为610-=ε): 3.已知函数表:用拉格朗日插值公式计算01.54.1==y x 以及所对应的近似值。
4. 已知函数表:用牛顿插值公式求)102(y 的近似值。
三 实验步骤(算法)与结果1#include<stdio.h>main(){float a[3][4]={20,2,3,24,1,8,1,12,2,-3,15,30};for(int i=0;i<=2;i++){for(int j=0;j<=2;j++){a[i][j]=(-1)*a[i][j];}}a[0][0]=20;a[1][1]=8;a[2][2]=15;float x=0,y=0,z=0;float X,Y,Z;for(int q=0;q<=1000;q++){X=(y*a[0][1]+z*a[0][2]+a[0][3])/a[0][0];Y=(x*a[1][0]+z*a[1][2]+a[1][3])/a[1][1];Z=(x*a[2][0]+y*a[2][1]+a[2][3])/a[2][2];x=X;y=Y;z=Z;}printf("方程组的解是X=%9.6f,Y=%9.6f,Z=%9.6f\n",X,Y,Z); }2#include<stdio.h>main(){float a[3][4]={20,2,3,24,1,8,1,12,2,-3,15,30};for(int i=0;i<=2;i++){for(int j=0;j<=2;j++){a[i][j]=(-1)*a[i][j];}}a[0][0]=20;a[1][1]=8;a[2][2]=15;float x=0,y=0,z=0;for(int q=0;q<=1000;q++){x=(y*a[0][1]+z*a[0][2]+a[0][3])/a[0][0];y=(x*a[1][0]+z*a[1][2]+a[1][3])/a[1][1];z=(x*a[2][0]+y*a[2][1]+a[2][3])/a[2][2];}printf("方程组的解是X=%9.6f,Y=%9.6f,Z=%9.6f\n",x,y,z); }3.#include<stdio.h>main(){float x[3]={1.14,1.36,1.45};float y[3]={5.65,4.15,3.14};float Y;Y=(1.4-x[2])*y[1]/(x[1]-x[2])+(1.4-x[1])*y[2]/(x[2]-x[1] );float X;X=(5.01-y[1])*x[0]/(y[0]-y[1])+(5.01-y[0])*x[1]/(y[1]-y[ 0]);printf("由拉格朗日插值公式得当X=1.4时,Y=%f,当Y=5.01时,X=%f\n",Y,X);}4.#include<stdio.h>main(){float x[5]={93.0,96.2,100.00,104.2,108.7};float y[5]={11.38,12.80,14.70,17.07,19.91};float dy1,dy2,dy3,dy4;float ddy1,ddy2,ddy3;float dddy1,dddy2;float ddddy;dy1=(y[0]-y[1])/(x[0]-x[1]);dy2=(y[1]-y[2])/(x[1]-x[2]);dy3=(y[2]-y[3])/(x[2]-x[3]);dy4=(y[3]-y[4])/(x[3]-x[4]);ddy1=(dy1-dy2)/(x[0]-x[2]);ddy2=(dy2-dy3)/(x[1]-x[3]);ddy3=(dy3-dy4)/(x[2]-x[4]);dddy1=(ddy1-ddy2)/(x[0]-x[3]);dddy2=(ddy2-ddy3)/(x[1]-x[4]);ddddy=(dddy1-dddy2)/(x[0]-x[4]);float Y;Y=y[3]+(102-x[3])*dy3+(102-x[3])*(102-x[2])*ddy2+(1002-x [3])*(102-x[2])*(102-x[1])*dddy1;printf("由牛顿插值公式得当X=102时,Y=%f\n",Y);}四实验收获与教师评语利用计算机实现了线性方程组的简单迭代法,赛德尔迭代法以及不等距节点下的牛顿插值公式以及拉格朗日插值公式。

实验报告一、实验目的1.迭代函数对收敛性的影响。
2.初值的选择对收敛性的影响。
二、实验题目1.用简单迭代法求方程01)(3=--=x x x f 的根。
分别化方程为如下等价方程: 31+=x x ;13-=x x ;x x 11+=;213-+=x x x 取初值5.10=x ,精度为410-,最大迭代次数为500,观察其计算结果并加以分析。
2.①用牛顿法求方程01)(3=-+=x x x f 在0.5附近的根,分别取初值1000,100,2,1,5.0,5.0,1,2,100,10000-----=x观察并比较计算结果,并加以分析。
②用牛顿法求方程0)(3=-=x x x f 所有根。
三、实验原理简单迭代法程序,牛顿迭代法程序。
四、实验内容及结果fun=inline('x^3-x-1');dfun=inline('3*x^2-1');-1000,x1=manewton(fun,dfun,-1000,1e-4) -100,x2=manewton(fun,dfun,-100,1e-4)-2,x3=manewton(fun,dfun,-2,1e-4)-1,x4=manewton(fun,dfun,-1,1e-4)-0.5,x5=manewton(fun,dfun,-0.5,1e-4) 0.5,x6=manewton(fun,dfun,0.5,1e-4)1,x7=manewton(fun,dfun,1,1e-4)2,x8=manewton(fun,dfun,2,1e-4)100,x9=manewton(fun,dfun,100,1e-4) 1000,x10=manewton(fun,dfun,1000,1e-4)3)在MA TLAB的主程序窗口输出以下结果:ans =-1000k=21x1 =0.682327804075895ans =-100k=16x2 =0.682327803903413ans =-2k=6x3 =0.682327803828020ans =-1k=5x4 =0.682327803828020ans =-0.500000000000000k=4x5 =0.682327803903932ans =0.500000000000000k=3x6 =0.682327803828347五、实验结果分析(1)实验1中用简单迭代法求方程01)(3=--=x x x f 的根:取初始值5.10=x 的时候,等价方程2和4是不收敛的。
实验目的:1.了解牛顿迭代法的基本概念。
2.了解牛顿迭代法的收敛性和收敛速度。
3.学习、掌握MATLAB软件的有关命令。
实验内容:用牛顿迭代法求方程321010-。
x x x++-=的近似根,误差不超过3实验准备:1.牛顿迭代法原理2.牛顿迭代法的几何解析3.牛顿迭代法的收敛性4.牛顿迭代法的收敛速度5.迭代过程的加速6.迭代的MATLAB命令MATLAB中主要用for,while等控制流命令实现迭代。
实验重点:1.牛顿迭代法的算法实现2.牛顿迭代法收敛性和收敛速度实验难点:1.牛顿迭代法收敛性和收敛速度实验方法与步骤:题目:用牛顿迭代法求方程3210++-=在x=0.5附近的近似x x x根,误差不超过310-。
牛顿迭代法的迭代函数为322()1()()321f x x x x g x x x f x x x ++-=-=-'++相应的MATLAB 代码为clear;x=0.5;for i=1:10x=x-(x^3+x^2+x-1)/(3*x^2+2*x+1)end可算的迭代数列的前3项0.5455,0.5437,0.5437。
经三次迭代,就大大超过了精度要求。
按要求运行结果如下:分析:1.改变初值:X=5,循环次数不变。
运行:精度不够,改变循环次数为10次。
再次运行:精度达到要求。
2.改变初值X=40,循环次数=10 运行精度不达要求,改变循环次数=30 再次运行精度达到要求。
总结分析:1. 经过实验,自己编程,先掌握熟悉迭代法的程序,然后编出牛顿迭代法实验的程序,学以致用。
2.在编程调试的过程中发现程序的错误,在修改程序中学会了耐心以及发现自己对该单元哪一部部分知识掌握得不好。
3.通过自己编程,既掌握记住了牛顿迭代法又掌握了Matlab知识,一举两得。
数值分析实验报告实验一、解线性方程组的直接方法——梯形电阻电路问题利用追赶法求解三对角方程组的方法,解决梯形电阻电路问题:电路中的各个电流{1i ,2i ,…,8i }须满足下列线性方程组:R V i i =- 22 210 252321=-+-i i i 0 252 432=-+-i i i 0 252 543=-+-i i i 0 252 654=-+-i i i 0 252 765=-+-i i i 0 252 876=-+-i i i 052 87=+-i i设V 220=V ,Ω=27R ,运用追赶法,求各段电路的电流量。
问题分析:上述方程组可用矩阵表示为:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------------00000001481.8522520000002520000002520000002520000002520000002520000002287654321i i i i i i i i问题转化为求解A x b =,8阶方阵A 满足顺序主子式(1,2...7)0i A i =≠,因此矩阵A存在唯一的Doolittle 分解,可以采用解三对角矩阵的追赶法!追赶法a=[0 -2 -2 -2 -2 -2 -2 -2]; b=[2 5 5 5 5 5 5 5];c=[-2 -2 -2 -2 -2 -2 -2 0]; d=[220/27 0 0 0 0 0 0 0];Matlab 程序function x= zhuiganfa( a,b,c,d )%追赶法实现要求:|b1|>|C1|>0,|bi|>=|ai|+|ci| n=length(b); u=ones(1,n); L=ones(1,n); y=ones(1,n); u(1)=b(1); y(1)=d(1); for i=2:nL(i)=a(i)/u(i-1);u(i)=b(i)-c(i-1)*L(i); y(i)=d(i)-y(i-1)*L(i); endx(n)=y(n)/u(n); for k=n-1:-1:1x(k)=(y(k)-c(k)*x(k+1))/u(k); end endMATLAB 命令窗口输入:a=[0 -2 -2 -2 -2 -2 -2 -2]; b=[2 5 5 5 5 5 5 5];c=[-2 -2 -2 -2 -2 -2 -2 0] d=[220/27 0 0 0 0 0 0 0];x= zhuiganfa(a,b,c,d )运行结果为:x =8.1478 4.0737 2.0365 1.0175 0.5073 0.2506 0.1194 0.0477存在问题根据电路分析中的所讲到的回路电流法,可以列出8个以回路电流为独立变量的方程,课本上给出的第八个回路电流方程存在问题,正确的应该是78240i i -+=;或者可以根据电路并联分流的知识,同样可以确定78240i i -+=。
迭代法的加速1 问题的提出在实际问题中,常常遇到非线性方程的求解问题,我们可以采用不动点迭代法求解非线性方程的根。
迭代法(iterative method )就是用某些收敛于所给问题的精确解的极限过程来采用逐步逼近的一种计算方法,其思想是构造不动点方程,然后得到迭代公式,反复用此公式算出近似值,使之逐步精确化。
使用迭代法的困难所在是计算量难以估计。
有时迭代过程虽然收敛,但由于收敛速度缓慢,使计算量变的很大而失去使用价值。
因此,迭代过程的加速具有重要意义。
迭代法加速,就是要寻找一种改进迭代法直接产生的序列的收敛速度的方法,使原来不收敛的序列变成收敛,使原来收敛较慢的序列变得收敛快。
2 迭代法的加速(Steffensen 加速迭代)2.1 将AitKen 加速技巧与不动点迭代相结合设是)*(*x x ϕ=是)(x ϕ的不动点,记,k k x x e -=*,利用中值定理有),('*)(*)(**11k kk k k k k x x x x x x x x e e ξϕϕϕ=--=--=++ k ξ在k x 与*x 之间。
通常)('k ξϕ依赖于k ,若)('x ϕ变化不大,设)('k ξϕC ≈,于是有 )*(*1k k x x C x x -≈-+)*(*12++-≈-k k x x C x x从上两式消去C ,则得kk k k x x x x x x x x --≈--+++****112 解得k k k k k k k k k k k k x x x x x x x x x x x x x +---≈+--=+++++++122112212)(2* 若记...,1,0,)(12211=+---=++++-k x x x x x x x k k k k k k k (2.3.1) 用序列}{k x -作为不动点*x 的新近似,一般说,它比不动点迭代法收敛更快。
其收敛性:0**lim =---x x x x k 推出其序列超收敛性;实际上迭代法(2.3.1)可改为....,1,0,2)(),(),(21=+---===+k x y z x y x x y z x y kk k k k k k k k k k ϕϕ(2.3.2) 称为Steffensen 迭代法,它是将原不动点迭代计算两次合并成一步得到,可改为另一种不动点迭代法),(1k k x x ψ=+(2.3.3)其中xx x x x x x +---=)(2))((])([)(2ϕϕϕϕψ(2.3.4) Steffensen 迭代具有比不动点迭代更高的收敛速度,若原迭代p 阶收敛的,则Steffensen 加速后p+1阶收敛。
迭代法的加速第一篇:迭代法的加速6.5迭代法的加速一、教学目标及基本要求通过对本节的学习,使学生掌握方程求根迭代法的加速。
二、教学内容及学时分配本章主要介绍线性方程求根的迭代法的加速方法。
要求1.了解数值分析的研究对象、掌握误差及有关概念。
2.正确理解使用数值方法求方程的解的基本思想、数学原理、算法设计。
3.了解插值是数值逼近的重要方法之一,正确理解每一种算法的基本思想、计算公式、算法设计、程序框图设计和源程序。
4.掌握数值积分的数学原理和程序设计方法。
5.能够使用数值方法解决一阶常微分方程的初值问题。
6.理解和掌握使用数值方法对线性方程组求解的算法设计。
三、教学重点难点1.教学重点:非线性方程迭代收敛性与迭代加速、牛顿法。
2.教学难点:迭代的收敛性。
四、教学中应注意的问题多媒体课堂教学为主。
适当提问,加深学生对概念的理解,迭代加速的算法实现。
五、教案正文6.1 迭代公式的加工迭代过程收敛缓慢,计算量将很大,需要进行加速。
设xk是根x*的某个近似值,用迭代公式校正一次得xk+1=ϕ(xk),假设ϕ'(x)在所考察得范围内变化不大,其估计值为L,则有:x*-xk+1≈L(x*-xk)⇒x*≈1Lxk+1-xk 1-L1-L1L=xk+1-xk,是比xk+1更好的近似根。
这样加工后1-L1-L有迭代公式xk+1的计算过程为:迭代xk+1=ϕ(xk)1Lxk+1-xk 1-L1-L1[ϕ(xk)-Lxk] 合并的xk+1=1-L改进xk+1=例3 P1336.2 埃特金算法上述加速方法含有导数ϕ'(x),不便于计算。
设将迭代值xk+1=ϕ(xk)再迭代一次,又得~xk+1=ϕxk+1,由于x*-~xk+1≈L(x*-xk+1)又x*-xk+1≈L(x*-xk),消去L得()x*-xk+1x*-xk(~xk+1-xk+1)2*~≈*⇒x≈xk+1-~*~x-xk+1x-xk+1xk+1-2xk+1+xk计算过程如下:迭代xk+1=ϕ(xk)迭代~xk+1=ϕxk+1 改进xk+1()(~xk+1-xk+1)2~ =xk+1-~xk+1-2xk+1+xk小结:这节课我们主要介绍了线性方程组迭代法加速的基本思想及其常用的几种迭代方法。