平面任意力系平衡方程及其应用

《机械基础》教案（2009～ 2010学年第二学期）学院山西省工贸学校系（部）机电系教研室教师梁少宁山西省工贸学校③学生学案课题名称：平面力系的平衡方程及其应用班级：姓名：(一)、工作任务：物体在平面力系作用下，不但有在平面内发生移动的可能性，而且有在平面内发生转动变化的可能性。

要使物体在平面任意力系作用下仍保持平衡状态，应满足什么条件？(二)、学习目标：1、理解平面任意力系的概念；掌握平面任意力系的平衡条件和平衡方程。

2、能应用平面任意力系平衡方程解决工程上的平衡问题；(三)、回答问题1、要使物体在平面任意力系作用下仍保持平衡状态，应满足什么条件？2、物体在平面力系作用下，在平面内都会发生那些移动方式？(四)、分析该资料，完成项目任务：一：平面力系的概念平面力系——各力作用线都在同一平面内的力系。

空间力系——各力作用线不在同一平面内的力系。

汇交力系——作用线交于一点的力系。

平行力系——作用线相互平行的力系。

一般力系——作用线既不完全交于一点又不完全平行的力系。

平面汇交力系的工程实例：二、力的分解按照平行四边形法则，两个共作用点的力，可以合成为一个合力，解是唯一的；但反过来，要将一个已知力分解为两个力，如无足够的条件限制，其解将是不定的。

1 、力在坐标轴上的投影注意:力的投影是代数量，它的正负规定如下：如由a到b(或由a1到b1)的趋向与x轴（或y轴）的正向一致时，则力F的投影F x（或F y）取正值；反之，取负值。

若已知力F在直角坐标轴上的投影F x、F y，则该力的大小和方向为力F可分解为F x、F y，可见利用力在直角坐标轴上的投影，可以同时表明力沿直角坐标轴分解时分力的大小和方向。

2、合力投影定理若刚体在平面上的一点作用着n个力F1，F2，…，F n，按两个力合成的平行四边形法则（三角形）依次类推，从而得出力系的合力等于各分力的矢量和。

即一般地，则其合力的投影合力投影定理——合力在某一轴上的投影等于各分力在同一轴上投影的代数和。

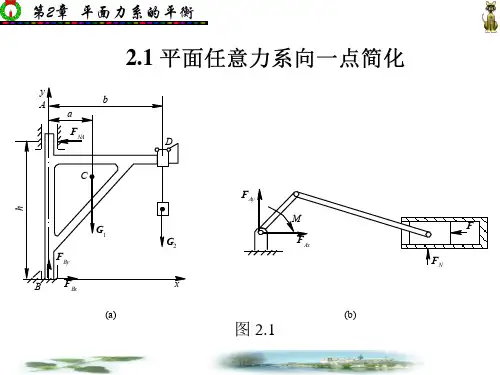
平面任意力系的平衡方程的三种形式一、概述1. 平面任意力系概念的简介在物体力学中，平面任意力系是一个很重要的概念。

平面任意力系是指一个物体在平面上受到多个力的作用，这些力可以是任意的方向和大小。

平面任意力系的研究对于分析物体的平衡和运动具有重要的意义。

2. 平衡方程的定义和作用平面任意力系的平衡方程是描述物体受力平衡的数学表达式。

通过平衡方程，可以求解物体受力的情况，从而进一步分析物体的平衡状态。

二、平面任意力系的平衡方程的三种形式1. 牛顿第一定律形式牛顿第一定律可以描述为：若物体受到多个力的作用，且这些力相互平衡，那物体将保持静止或匀速直线运动。

根据这一定律，可以得出平衡方程的第一种形式。

即对于平面任意力系，受力平衡时，力在x、y方向上的合力均为0，可以用数学公式表示为：ΣFx = 0；ΣFy = 0。

式中ΣFx表示x方向上的合力，ΣFy表示y方向上的合力。

当ΣFx和ΣFy都等于0时，物体在受力平衡状态。

2. 平衡方程的角度形式平衡方程的角度形式是指从物体受力的角度出发，建立平衡方程。

在平面任意力系中，受力平衡时，物体对于一个特定点的力矩的和为0。

力矩的和可以表示为：ΣM = 0。

式中ΣM表示力矩的和。

根据力矩的定义，可以将力矩表示为力乘以力臂的乘积。

可以将平衡方程的角度形式表示为：ΣM = ΣF × d = 0。

式中d表示力臂的长度。

当ΣM等于0时，说明物体对于特定点的力矩平衡，即物体处于受力平衡状态。

3. 用平面力系的分解形式建立平衡方程在平面任意力系中，可以将作用在物体上的力进行分解，将力分解成在x、y方向上的分力和分力的合力。

根据此方法，可以建立平衡方程的分解形式：ΣFx = 0；ΣFy = 0。

这种形式的平衡方程适用于多种情况，可以将力分解成任意方向上的分力，从而更加灵活地分析物体的受力情况和平衡状态。

三、平衡方程的应用1. 建立平面任意力系的平衡方程在实际问题中，可以通过观察和分析物体受力的情况，建立平衡方程，从而求解物体受力平衡的情况。

课题 1.4平面力系的平衡方程及应用
课时 1 班级21机电3/4班课型新课时间2021年10月22日
教学目标知识目标：熟记任意力系和汇交力系平衡的条件能力目标：能通过列平衡方程计算力的大小
德育目标：提高合作探究能力，增强合作意识
教学重点任意力系和汇交力系平衡的条件
教学难点根据平衡方程进行计算
教法直观教学法
学法小组合作探究
教学评价师生互评，小组互评
教具多媒体课件，教具，动画
教学过程及主要教学内容师生活动一、汇交力系平衡方程及图示：
所有的力都汇聚于一点的称为汇交力系。

二、平面任意力系及图示：教师：精讲
互问互答
学生：小组合作学生：组间竞赛
三、例题：
作业减速器中的齿轮轴受力如图所示，已知F、a，求：（1）绘制齿轮轴的受力图；（2）求支座A/B的约束力。

课后反思（教学收获、特色创新、存在不足、改进措施）。