理论力学4-4-平面力系的平衡方程
- 格式:pdf
- 大小:260.97 KB
- 文档页数:3


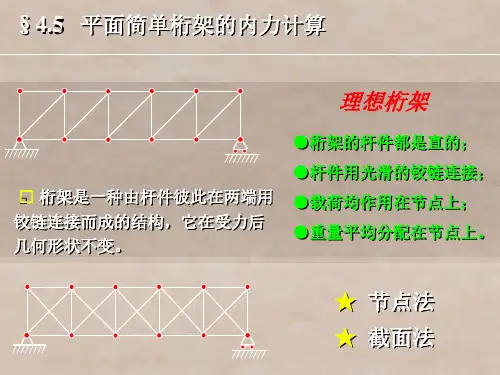







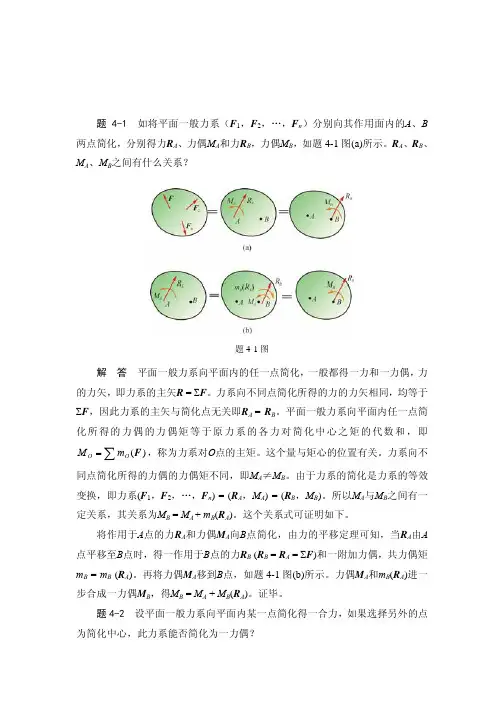
第四章 平面一般力系题4-1 如将平面一般力系(F 1,F 2,…,F n )分别向其作用面内的A 、B 两点简化,分别得力R A 、力偶M A 和力R B ,力偶M B ,如题4-1图(a)所示。
R A 、R B 、M A 、M B 之间有什么关系?题4-1图解 答 平面一般力系向平面内的任一点简化,一般都得一力和一力偶,力的力矢,即力系的主矢R = ΣF 。
力系向不同点简化所得的力的力矢相同,均等于ΣF ,因此力系的主矢与简化点无关即R A = R B 。
平面一般力系向平面内任一点简化所得的力偶的力偶矩等于原力系的各力对简化中心之矩的代数和,即,称为力系对O 点的主矩。
这个量与矩心的位置有关。
力系向不同点简化所得的力偶的力偶矩不同,即M )(F O O m M ∑=A ≠M B 。
由于力系的简化是力系的等效变换,即力系(F 1,F 2,…,F n ) = (R A ,M A ) = (R B ,M B )。
所以M A 与M B 之间有一定关系,其关系为M B = M A + m B (R A )。
这个关系式可证明如下。
将作用于A 点的力R A 和力偶M A 向B 点简化,由力的平移定理可知,当R A 由A 点平移至B 点时,得一作用于B 点的力R B (R B = R A = ΣF )和一附加力偶,共力偶矩m B = m B (R A )。
再将力偶M A 移到B 点,如题4-1图(b)所示。
力偶M A 和m B (R A )进一步合成一力偶M B ,得M B = M A + M B (R A )。
证毕。
题4-2 设平面一般力系向平面内某一点简化得一合力,如果选择另外的点为简化中心,此力系能否简化为一力偶?解 答 如果平面一般力系向某点简化得一合力,即表明原力系与此合力等效。
如果力系选择另外的点为简化中心,若能简化为一力偶的话,则又表明力系与此力偶等效,因此力系的合力也应与力偶等效。
事实上,一个力是不能与一个力偶等效的。
1第3章 力系的平衡 3.1 主要内容空间任意力系平衡的必要和充分条件是:力系的主矢和对任一点的主矩等于零,即 0=R F 0=O M 空间力系平衡方程的基本形式 0,0,0=∑=∑=∑z y x F F F 0)(,0)(,0)(=∑=∑=∑F F F z y x M M M空间汇交力系平衡的必要和充分条件是:力系的合力 0=R F空间汇交力系平衡方程的基本形式0,0,0=∑=∑=∑z y x F F F空间力偶系平衡的必要和充分条件是:各分力偶矩矢的矢量和 0=∑i M空间力偶系平衡方程的基本形式 0)(,0)(,0)(=∑=∑=∑F F F z y x M M M平面力系平衡的必要和充分条件:力系的主矢和对于任一点的主矩都等于零,即:0=∑='F F R;0)(=∑=F O O M M 平面力系的平衡方程有三种形式:基本形式: 0)(,0,0=∑=∑=∑F M F F O y x二矩式: 0)(,0)(,0=∑=∑=∑F M F M F B A x (A 、B 连线不能与x 轴垂直)三矩式: 0)(,0)(,0=∑=∑=∑F M F M M C B A (A 、B 、C 三点不共线)平面力系有三个独立的平衡方程,可解三个未知量。
平面汇交力系平衡的必要和充分条件是合力为零,即0=∑=F F R 平衡的解析条件:各分力在两个坐标轴上投影的代数和分别等于零,即0,0=∑=∑y x F F两个独立的平衡方程,可解两个未知量。
平面力偶系平衡的必要和充分条件为:力偶系中各力偶矩的代数和等于零,即∑=0Mi一个独立的平衡方程,可解一个未知量。
3.2 基本要求1.熟练掌握力的投影,分布力系的简化、力对轴之矩等静力学基本运算。
2.能应用各种类型力系的平衡条件和平衡方程求解单个刚体和简单刚体系统的平衡问题。
对平面一般力系的平衡问题,能熟练地选取分离体和应用各种形式的平衡方程求解。
3.正确理解静定和超静定的概念,并会判断具体问题的静定性。
理论力学重点总结理论力学重点总结绪论1.学习理论力学的目的:在于掌握机械运动的客观规律,能动地改造客观世界,为生产建设服务。
2.学习本课程的任务:一方面是运用力学基本知识直接解决工程技术中的实际问题;另一方面是为学习一系列的后继课程提供重要的理论基础,如材料力学、结构力学、弹性力学、流体力学、机械原理、机械零件等以及有关的专业课程。
此外,理论力学的学习还有助于培养辩证唯物主义世界观,树立正确的逻辑思维方法,提高分析问题与解决问题的能力。
第一章静力学的基本公理与物体的受力分析1-1静力学的基本概念1.刚体:即在任何情况下永远不变形的物体。
这一特征表现为刚体内任意两点的距离永远保持不变。
2.质点:指具有一定质量而其形状与大小可以忽略不计的物体。
1-3约束与约束力1.自由体:凡可以在空间任意运动的物体称为自由体。
2.非自由体:因受到周围物体的阻碍、限制不能作任意运动的物体称为非自由体。
3.约束:力学中把事先对于物体的运动(位置和速度)所加的限制条件称为约束。
约束是以物体相互接触的方式构成的,构成约束的周围物体称为约束体,有时也称为约束。
4.约束力:约束体阻碍限制物体的自由运动,改变了物体的运动状态,因此约束体必须承受物体的作用力,同时给予物体以相等、相反的反作用力,这种力称为约束力或称反力,属于被动力。
5.单面约束、双面约束:凡只能阻止物体沿一方向运动而不能阻止物体沿相反方向运动的约束称为单面约束;否则称为双面约束。
单面约束的约束力指向是确定的,即与约束所能阻止的运动方向相反;而双面约束的约束力指向还决定于物体的运动趋势。
6.柔性体约束:为单面约束。
只能承受拉力,作用在连接点或假想截割处,方向沿着柔软体的轴线而背离物体,常用符号F T表示。
(绳索、胶带、链条)7.光滑接触面(线)约束:为单面约束,其约束力常又称为法向约束力。
光滑接触面(线)的约束力只能是压力,作用在接触处,方向沿着接触表面在接触处的公法线而指向物体,常用符号F N表示。