正弦交流电的相量图表示法.

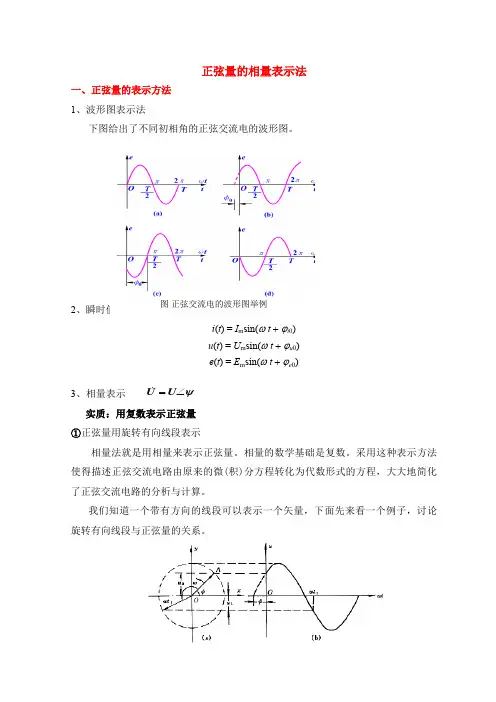
正弦量的相量表示法一、正弦量的表示方法1、波形图表示法下图给出了不同初相角的正弦交流电的波形图。

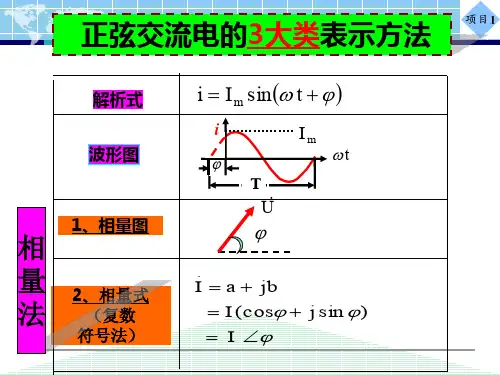
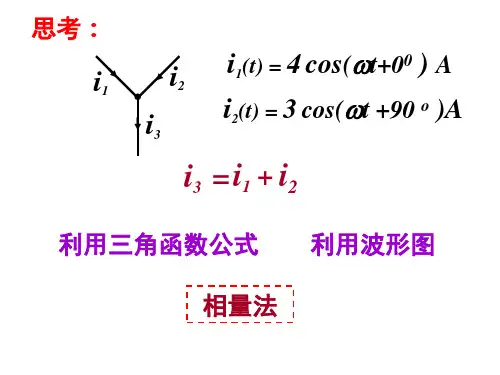
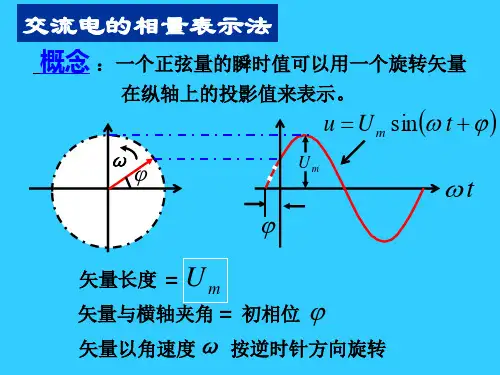
2、瞬时值表达式 i (t ) = I m sin(ω t + ϕi 0)u (t ) = U m sin(ω t + ϕu 0)e (t ) = E m sin(ω t + ϕe 0)3、相量表示实质：用复数表示正弦量①正弦量用旋转有向线段表示相量法就是用相量来表示正弦量。

相量的数学基础是复数。

采用这种表示方法使得描述正弦交流电路由原来的微(积)分方程转化为代数形式的方程，大大地简化了正弦交流电路的分析与计算。

我们知道一个带有方向的线段可以表示一个矢量，下面先来看一个例子，讨论旋转有向线段与正弦量的关系。

图 正弦交流电的波形图举例 ψU U ∠=设正弦量U= U m sin(ωt +ψ)若: 有向线段长度 = Um有向线段与横轴夹角 = 初相位ψ有向线段以速度ω按逆时针方向旋转则:该旋转有向线段每一瞬时在纵轴上的投影即表示相应时刻正弦量的瞬时值。

例如：在t =t 0时，U 0=U m sin(ωt 0+ψ)在t=t l 时，U 1=U m sin ；(ωt 1+ψ)正弦量可用有向线段表示，而有向线段又可用复数表示，所以正弦量可用复数来表示。

② 复数的几种表示形式在一个直角坐标系中，设：横轴为实轴，单位用+1表示；纵轴为虚轴，单位用+j 表示，则构成复数平面(又称复平面)。

图所示的有向线段A ，其复数表示式为：a ．代数式 A=α+ jba=rcosψ ，b=rsinψb ． 三角式根据欧拉公式：c ．指数式 A= re j ψd ． 极坐标式一个复数可用代数式、三角式、指数式和极坐标式四种表示形式，四者可以互相 ψr A =ψψψsin j cos e j +=可得:ab ψarctan =22b a r +=复数的模 复数的辐角 )sin j (cos sin j cos ψψr ψr ψr A +=+=,e e 2cos j j ψψψ-+=2j sin j j ψψψ--=e e转换。

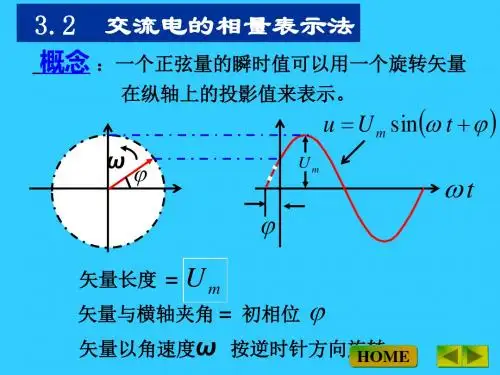
第三章正弦交流电路§3-2 正弦量的相量表示法前面讲述过正弦量的两种基本表示方法，分别用解析式和波形图表示。

前者方便于求出正弦量的瞬时值，而后者形象直观。

但在进行几个正弦量的加减等运算时，用这两种表示法分析就显得比较复杂。

在正弦交流电路中,所有的电压、电流、电动势都是和电源同频率的正弦量，也就是说频率往往是已知的，只要确定了这些正弦量的最大值（有效值）和初相，那么正弦量就完全确定了。

由此，在本节引入正弦量的相量表示法，就是利用复数来表示正弦交流量的一种方法。

它是交流电路分析计算中最为方便的一种。

一、复数（一）复数的四种表示形式1、复数的代数形式。

jba A +=2、复数的三角形式)sin (cos sin cos ψψψψj A A j A A +=+=ψj eA A =ψ∠=A A 3、复数的指数形4、复数的极坐标形式（二）复数的运算1、加减运算复数相加（或相减）时，将实部与实部相加（或相减），虚部与虚部相加（或相减）。

设两个复数：11111ψ∠=+=A jb a A 22222ψ∠=++=A jb a A )()()()(2121221121b b j a a jb a jb a A A ±+±=+±+=±2、乘除运算通常情况下，将复数转化为极坐标形式（或指数形式）来进行乘除运算，更加方便些。

相乘运算时，乘积的模等于各复数的模相乘，乘积的辐角等于各复数幅角相加；相除运算时，商的模等于各复数的模相除，商的辐角等于各复数幅角相减。

即)(2121221121ψψψψ+∠=∠⨯∠=A A A A A A )(212121ψψ-∠=A A A A32.17101j A -=566.82j A +=212121,,A A A A A A -【例3-4】已知两复数求602032.17101-∠=-=j A3010566.82∠=+=j A 7.834.1232.1234.1)532.17()66.810(21∠=+=----=-j j A A 29023010602021j A A =-∠=∠-∠=1002.173302003010602021j A A -=-∠=∠⨯-∠= 解二、正弦量的相量表示法在正弦量的三要素中，只有有效值（或最大值）和初相两个要素是待求的未知量，而数学中的每个复数对应着唯一的模和幅角两个要素，因此，频率已知的正弦量和复数之间存在着对应的关系。

正弦交流电的表示法2.1.2 正弦量的相量表示法如前所述，一个正弦量由幅值、角频率和初相位三个要素确定，而正弦量的这些特征，可以用正弦波和三角函数表示出来。

除此之外，还可以用相量表示，复数是相量的基础。

（1）复数如图2-6所示，一复数A，a1为其实部，a2为其虚部，a为其长度，则复数A可用四种形式来表示：图2-6 复平面上表示复数A①代数式A=a1+j a2（2-8）为虚单位。

②三角函数式令复数A的模|A|=a，φ角是复数A的辐角，有A=｜A｜（cosφ+jsinφ）=a（cosφ+jsinφ）（2-9）式中，，，③指数式根据欧拉公式e jφ=cosφ+jsinφA=a e jφ（2-10）④极坐标式极坐标式是复数指数式的简写，这四种复数的表示形式，可以相互转换。

复数的指数形式（或极坐标形式）与复数的三角函数式之间可以通过欧拉公式进行转换，指数形式（或极坐标形式）要变换成代数式可以通过欧拉公式进行转换；代数式变换成指数形式（或极坐标形式）可以通过式（2-9）进行转换。

（2）正弦量的相量表示用复数来表示正弦量的方法称为正弦量的相量表示法，即用复数的模来表示正弦量的幅值（最大值或有效值），用复数的辐角来表示正弦量的初相位。

只有同频率的正弦量用相量进行分析计算才有意义，它使得正弦交流电路的分析和计算变得更为简单。

在线性正弦交流电路中，各部分的电流和电压都是同频率的正弦量。

因为频率不变，所以可以用相量来表示正弦量。

正弦量的相量形式是用大写字母上面加小圆点表示。

例如，“”“”“”等。

同理，可自行写出和相量。

相量、、称为有效值相量，、、称为最大值相量或幅值相量。

相量在复平面上的几何图形叫做相量图，如图2-7所示。

图2-7 正弦量的相量图同频率的正弦量，由于它们之间相位的相对位置不变，即相位差不变，因此可以将它们的相量画在同一个坐标上。

不同频率的正弦量，用相量表示时，不能画在同一相量图上。

（3）相量运算相量的运算规则符合复数运算中的交换律、结合律和分配律等。