交流电的相量表示法(2)

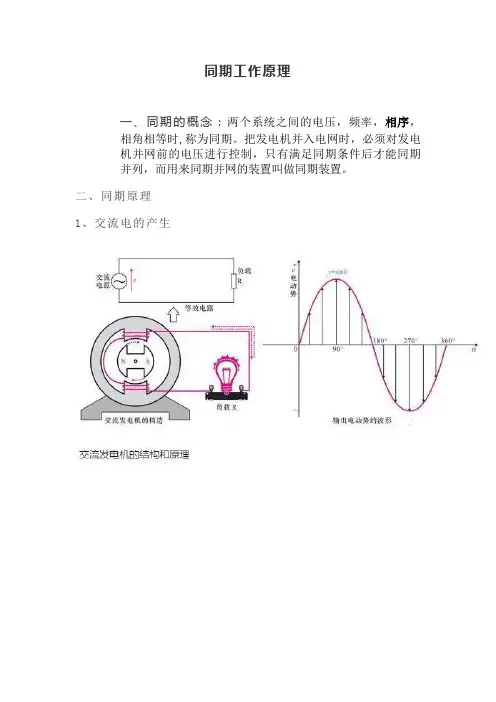
同期工作原理
一、同期的概念：两个系统之间的电压，频率，相序，
相角相等时,称为同期。

把发电机并入电网时，必须对发电
机并网前的电压进行控制，只有满足同期条件后才能同期
并列，而用来同期并网的装置叫做同期装置。

二、同期原理
1、交流电的产生
二、交流电的三种表示方法
1、数学式表达方法
U=U m sin（ωt+ψi）
2、波形表示法
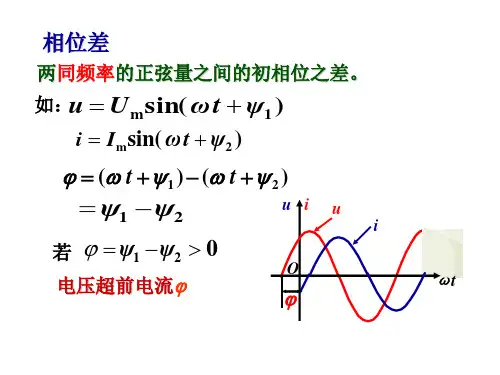
3、相位表示法
三、交流电的三要素：电压幅值、频率、初相位角
U
U1 △U
0 U2
U
U
U1
△U
U2
0 T
T
T
电压频率不一样
我公司二期同期整定值：允许频差0.15HZ；允许压差5%U n；初相角20度以内。

四、同期操作票：先调电压，再调频率，初相位不用调，提前合闸时间发出合闸脉冲。

五、同期过程（视频）
1、相量旋转原理：假设系统3000转/分，发电机3006转/分，1÷50×X=1÷50.1×（X+1）得X=500转500×0.02=10秒
2、同期装置和同期表的区别
六、同期二次图（图纸）
八、开关的合闸/跳闸回路（图纸）
1、同期合闸
2、NCS合闸
九、同期事故（内蒙古通辽电厂和湖北襄樊电厂和贵州鸭溪电厂）发电机中性点断线分析：（图纸）
课堂习题：
1、同期三要素？
2、5012开关合闸先后经过了哪些设备？。

三相电压的相量表示是将时间上连续变化的三相正弦交流电压以复数形式表达，这种方法可以直观地描述各相电压在幅值、频率以及相位上的关系。

在电力系统分析中，通常采用极坐标或直角坐标（也称作笛卡尔坐标）来表示。

极坐标表示：
对于星形连接（Y接法）的三相电源或负载，其相电压相对于同一基准（例如A相）的相量表示为：
- A相：UA = V∠0°
- B相：UB = V∠-120°
- C相：UC = V∠120°
这里的V代表每相的有效电压幅值，角度表示的是相对于A 相的相位差，按照逆时针方向，B相滞后A相120度，C相超前A相120度。

直角坐标表示：
在静止对称坐标系（如αβγ坐标系或dq0坐标系）中，也可以转换成直角坐标形式表示，但此处不涉及具体的坐标变换过程。

对于三角形连接（Δ接法）的三相电压，线电压与相电压之间的关系如下：
- 线电压UAB = UA - UB = 380∠30° (假设有效线电压为380V)
- 线电压UBC = UB - UC = 380∠-90°
- 线电压UCA = UC - UA = 380∠150°
相量图中，三个电压相量按照120度均匀分布，且同时绕着同一个轴以相同的角速度逆时针旋转，这个角速度对应的就是系统的角频率ω（对于50Hz的交流电，ω=2π×50 rad/s）。

通过相量图和相量计算，能够简化复杂电路的分析和计算。

简述正弦交流电的三种表示方法1.引言1.1 概述概述部分的内容可以按照以下方式编写:引言部分是文章的开篇，目的是为读者提供对后续内容的整体了解。

在这篇文章中，我们将讨论正弦交流电的三种表示方法。

正弦交流电是工程技术领域中常见的电信号类型之一，广泛应用于电力系统、电子电路和通信系统等领域。

正弦交流电具有周期性的特点，可以表示为周期性变化的信号。

对于正弦交流电的表示方法，研究者们提出了多种不同的方式。

本文将详细介绍其中的三种主要表示方法，分别是：1. 直角坐标系表示法：通过在直角坐标系中绘制电压或电流随时间的变化曲线，来表示正弦交流电的变化规律。

这种方法直观且易于理解，可以清晰展示电压或电流的振幅、频率和相位等重要参数。

2. 极坐标系表示法：将正弦交流电视为一个旋转的向量，通过描述其振幅和相位差来表示。

极坐标系表示法适用于描述相位关系的问题，对于分析电路中的相位差和频率变化等现象非常有用。

3. 复数表示法：利用复数的实部和虚部，将正弦交流电转化为复数形式进行表示。

这种表示方法在电路分析和计算中非常高效，可以通过简单的复数运算得到电流和电压的各种参数，极大地简化了电路分析的过程。

本文将分别对上述三种表示方法进行详细阐述，分析其优缺点以及适用场景，旨在让读者全面了解正弦交流电的不同表示方法，并为进一步深入研究和应用提供参考。

接下来，我们将介绍文章的结构以及各个章节的具体内容。

1.2文章结构文章结构部分的内容可以包括以下内容：文章结构是指整篇文章内容的组织和安排方式，它包括了引言、正文和结论三个主要部分。

通过清晰的文章结构，读者可以更好地理解文章的内容，把握文章的逻辑关系和主旨。

引言部分为文章提供了一个引人注目的开篇，引发读者的兴趣，并对正文的内容进行简单概述。

在这个部分，我们将对正弦交流电的三种表示方法进行简要的介绍。

正文部分是文章的重点，用来详细阐述正弦交流电的三种表示方法。

在正文中，我们将分别介绍第一种、第二种和第三种表示方法，详细讲解它们的原理、特点和应用场景。

对称三相交流电压的时域表达式和相量表达式在电力系统中，三相交流电压是一种常见的电力信号。

了解对称三相交流电压的时域表达式和相量表达式对于电力系统的分析和运行非常重要。

本文将深入探讨这一主题，从简到繁，由浅入深地介绍对称三相交流电压的时域表达式和相量表达式，以便读者能更深入地理解。

1. 对称三相交流电压的时域表达式对称三相交流电压由三个正弦波电压相位相差120度组成。

对称三相交流电压的时域表达式可表示为：\[V_a = V_m \cdot \sin(\omega t)\]\[V_b = V_m \cdot \sin(\omega t - \frac{2}{3} \pi)\]\[V_c = V_m \cdot \sin(\omega t + \frac{2}{3} \pi)\]其中，\(V_a\)、\(V_b\)、\(V_c\) 分别代表A相、B相、C相的电压；\(V_m\) 代表电压的峰值；\(\omega\) 代表角频率；\(t\) 代表时间。

时域表达式告诉我们，对称三相交流电压是随着时间周期性变化的正弦波电压。

A相、B相、C相的电压之间相位差120度，呈现对称关系。

2. 对称三相交流电压的相量表达式对称三相交流电压的相量表达式是一种通过向量表示三个电压之间相互关系的方法。

相量表达式可以更直观地展示电压之间的幅值和相位关系。

假设三相电压的相量分别为\(V_a\)、\(V_b\)、\(V_c\)，则其相量表达式为：\[V_a = V_{an} \angle 0^\circ\]\[V_b = V_{bn} \angle (-120^\circ)\[V_c = V_{cn} \angle 120^\circ\]其中，\(V_{an}\)、\(V_{bn}\)、\(V_{cn}\) 分别代表A相、B相、C相的电压幅值；角度表示电压之间的相位差。

相量表达式可以将三相电压用向量形式表示，从而清晰地展示电压之间的相位关系。

第二节 交流电的表示法一、 基础知识梳理1．解析式表示法：u=U m sin(ωt+φu ) ，i=I m sin(ωt+φi ) 。

根据三要素，可以方便的写出解析式。

解析式表示法是表示正弦交流电最简洁，但也是最精确的表示法。

2．图像表示法：用正弦曲线直观的表示正弦交流电的表示方法。

根据波形图，可以写出三要素，反之也可以。

（如图所示）图像表示法是表示正弦交流电最形象的表示法。

3．相量表示法：为了分析正弦交流电路时计算的方便，我们人为引入了正弦交流电的相量表示法。

复数正弦量复数复数表示正弦量，这种复数叫做正弦量的“相量”用 表示。

用复数画的向量图称“相量图”。

只有正弦交流电路才应用相量法。

)(b a A 22长度+=)(a b tg 1幅角-=有效值:初相角角度:有效值模数:初相位幅角:I,E ,U A )30t ωsin(1002i e 100I 0130J 10+=⇒= V )45t ωsin(2202u e 220U 0145J 10-=⇒=-A)120t ωsin(502i 20501I 0202+=⇒= tV ωsin 3802u 380U 22=⇒=相量形式是当频率一定时，正弦量瞬时值表达式的代表符。

所以，采用相量法后，交流电路和直流电路中的定律和公式在形式上是相似的。

所不同的是，交流电在计算时应按复数运算法则进行。

二、 应用举例应用一：相量表示法应用分析：相量形式：用复数的极坐标形式来表示交流量正弦量可以用振幅相量或有效值相量表示，但通常用有效值相量表示。

有效值相量表示法是用正弦量的有效值做为相量的模(长度大小)、用初相角做为相量的幅角，通式为：e E E ϕ∠= u U U ϕ∠= iI I ϕ∠=相量图形式：把交流电的相量画到复平面中。

（同频率的可画在同一复平面中）例1：写出下列正弦电压的相量(1) .U =10∠0 V(2) .U =10∠/2V (3) .U =10∠-/2V(4) .U =10∠-3/4 V 举一反三：如图所示为两个同频率的正弦交流电压u 1、u 2的波形，求u 1、u 2的解析式和相量形式，并画出相量图。