装配线的平衡具体计算题分解

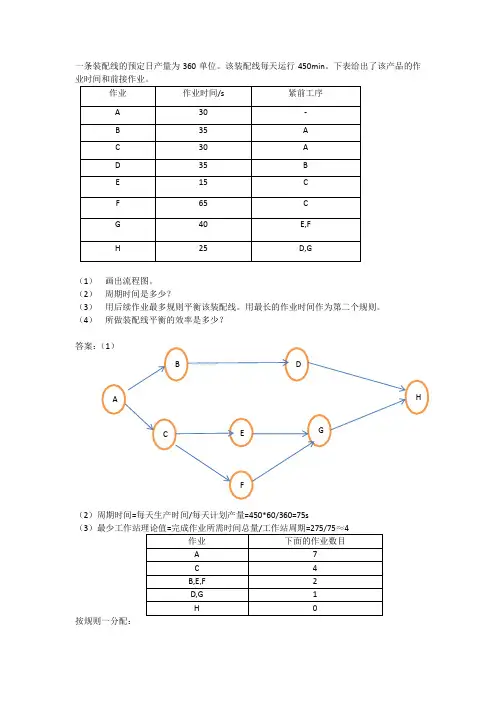
画装配工序先后顺序图及装配线平衡画装配工序先后顺序图装配线的平衡N:装配线的工位数C: 节拍: 第i 项任务的作业时间4）装配线平衡的步骤：a.确定装配线的节拍节拍c= 计划起有效工作时间/计划期产量注意：有效工作时间除去必要的停歇；产量包含不合格品。

b. 计算装配线需要的最少工位数N = [产品装配总作业时间/节拍] = [ ]c. 组织工位向每一个工位分配任务时必须满足下列条件：保证人物之间的顺序关系；每个工位分配的任务作业之和不能大于节拍；各工位的单件作业时间应尽量相等或接近节拍；使工位数尽量少后续任务数多的工作优先安排；加工时间长的工作优先安排。

d.计算装配线的负荷系数BD 为装配线平衡损失系数 ηη-=⨯=∑1BD C N ti一装配线计划每小时装配200件，每小时工作时间为50分钟，下表是各个工序及关系。

求（1）画出装配工序顺序图（2）计算装配线的节拍（3）计算每小时装配200件的最小工序数（4）进行装配线平衡，使时间损失率最小装配线工序及作业时间工序作业时间紧前工序a 0.2 -b 0.05 -c 0.15 -d 0.06 -e 0.03 a,bf 0.08 c,dg 0.12 e,fh 0.05 -i 0.05 -j 0.12 h,ik 0.15 jL 0.08 k解答：（1）画图略（2）节拍C = 50/200=0.25(分钟/件)（3）最小工作地数N = [工序作业时间之和/节拍]=[（0.2+0.05+0.15+0.06+0.03+0.08+0.12+0.05+0.05+0.12+0.15+0.08)/0.25] = 5 (4) 平衡结果：(a,b),(c,d,e),(f,g),(h,i),(j),(k,L).效率=83%。

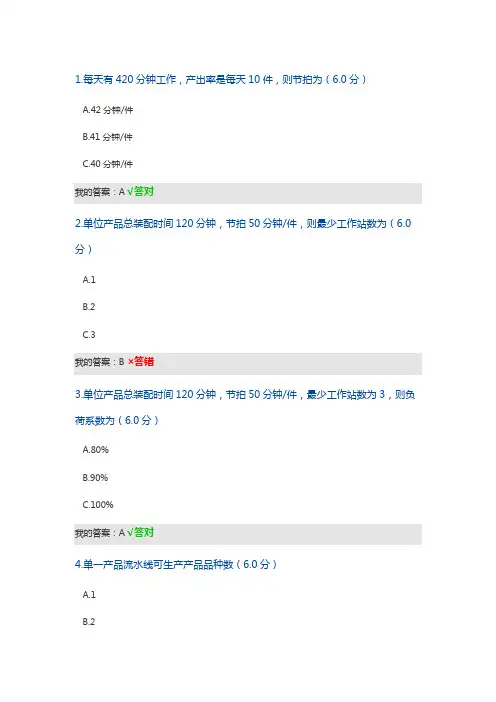
1.每天有420分钟工作，产出率是每天10件，则节拍为（6.0分）A.42分钟/件B.41分钟/件C.40分钟/件我的答案：A√答对2.单位产品总装配时间120分钟，节拍50分钟/件，则最少工作站数为（6.0分）A.1B.2C.3我的答案：B×答错3.单位产品总装配时间120分钟，节拍50分钟/件，最少工作站数为3，则负荷系数为（6.0分）A.80%B.90%C.100%我的答案：A√答对4.单一产品流水线可生产产品品种数（6.0分）A.1B.2我的答案：A√答对5.某道工序加工时间为9分钟，节拍为5分钟/件，则这道工序需要设备数（6.0分）A.1.8台B.2台我的答案：B√答对1.狭义的生产过程指（8.0分））A.生产技术准备B.原料投入C.在制品生产我的答案：BC√答对2.生产过程的适应性指适应（8.0分））A.品种变化能力B.产量变化能力C.设备更新我的答案：AB√答对3.组织生产的基本要求（8.0分））A.连续性B.平行性D.均衡性E.适应性我的答案：ABCDE√答对4.广义的生产过程指（8.0分））A.生产技术准备B.原料投入C.在制品生产我的答案：ABC√答对5.生产过程的构成（8.0分））A.技术准备过程B.基本生产过程C.辅助生产过程D.生产服务过程E.副业生产我的答案：ABCD×答错1.生产过程的适应性指适应品种和产量变化的能力。

（6.0分）我的答案：正确√答对2.生产过程的均衡性指在相等的时间间隔生产的产量大致相等或递增数量的产品。

（6.0分）我的答案：正确√答对3.广义的生产过程指从生产技术准备开始直到把产品制造出来为止的全部过程。

（6.0分）我的答案：正确√答对4.节拍是指流水线上连续生产两件制品的时间间隔。

（6.0分）我的答案：错误×答错5.狭义的生产过程指从原材料投入生产开始直到产品最后制造出来为止的全部过程。

（6.0分）我的答案：正确√答对。

线性规划法实例：运输问题设有三个产煤地（简称产地)A1，A2，A3，其产量分别为9吨，10吨，6吨，另有四个城市(简称销地）B1,B2，B3,B4需要销煤，其销量分别为6吨，6吨,3吨，10吨，已知从每个产地到各销地的单位运价如表4所示。

有假定运费与运量成正比，问应如何安排调拨计划，才能使总的运费最省？表4单位运价(吨/元）线性规划法列出目标函数和约束方程如下：343332312423222114131211425425339410m in x x x x x x x x x x x Z ++++++++++=步骤1.建立运输矩阵2。

用最低成本法—-确定初始方案 3。

优化初始方案（闭回路法） 4。

计算总费用约束条件：s.t)4,3,2,1;3,2,1(0103666109342414332313322212312111343332312423222114131211==≥=++=++=++=++=+++=+++=+++j i x x x x x x x x x x x x x x x x x x x x x x x x x ij ∑=ijij Q P Z min装配线平衡方法J型玩具马车要在一个传送带上组装，每天需生产500辆。

每天的生产时间为420分钟,表2中列出了玩具马车的组装步骤及其时间。

请根据节拍和作业次序的限制,求使工作站数量最少的平衡方式(2）计算节拍.必须把时间单位换算为秒，因为作业时间是以秒表示的。

r=每天的工作时间/每天的产量=60（秒)×420/500（辆）=50。

4秒/辆（3）工作站数量的理论最小值（实际可能大些）Smin=[T/r]=195秒/50.4秒=[3.87]=4（取整):由最后一道工序，按编组过程反方向检查每一工作地，用于寻找本分支节点上是否存在Sij<S’(分支定界数4)的节点。

本问题不存在Sij〈S'的节点，则：S’为最优，即节点数为4。

装配线的平衡一、流水生产的基本概念一）、流水生产的特点二）、流水生产线的种类三）、流水生产的组织二、装配线的平衡一、流水生产的基本概念流水生产——是劳动对象按照一定的工艺过程、规定的顺序和速度，连续不断地通过各个工作地进行加工，完成工序作业的一种生产过程组织形式。

流水生产是将高度的对象专业化的生产组织和劳动对象的平行移动方式有机地结合起来。

流水生产的主要特点是：1，各工作地按照劳动对象的加工顺序排列。

2．每个工作地固定地完成一道和少数几道工序，工作地的专业化程度高。

3．流水线上各工序的加工时间之间成相等或整数倍数关系。

4，按照一定的节拍进行生产。

流水生产线的种类1．按流水线的连续程度——连续流水线和间断流水线2．按在流水线上加工对象的数目——单一对象流水线和多对象流水线3．按流水线上的劳动对象是否移动——制件固定流水线和制件移动流水线4．按流水线的节拍——强制节拍流水线和自由节拍流水线5，按流水线的机械化程度——手工流水线和机械化流水线组织流水生产的条件组织流水生产需要具各一定条件，这些条件主要有：1），产品结构和工艺要相对稳定。

2）．产品、零件和部件的产量要大，足以保证工作地的正常负荷。

在产品品种多，产量不大的企业中，组织流水生产时，可通过成组工艺来增大同种零件的产量三、装配线平衡（一）、为什么要进行生产线平衡?浪费时间资源忙闲不均，引起矛盾浪费人（二）生产线平衡的目的物流快速﹐缩短生周期减少或消除物料或半成品周转场所消除生产瓶颈﹐提高作业效率提升工作士气﹐改善作业秩序稳定产品质量（三）装配线平衡的技巧1、如何消除瓶颈1）作业分割——将此作业的一部分分割出来移至工时较短的作业工序。

2）利用或改良工具﹑机器——将手工改为工具；或半自动或全自动机器；或在原有工具；夹具做改善；自可提升产量﹐缩短作业工时。

3）提高作业者的技能——运用工作教导，提升作业者的技能4 ）调换作业者——调换效率较高或熟练作业人5 ）增加作业者——上面几项都做了﹐还未达到理想﹐可能就得考虑增加工序人手了。

生产运作管理共有五道计算类型题：标黄色的表示做题时，必须要阐述写清的。

一、装配线平衡的方法1.（在答题纸上划出题中要求的网络图）2.节拍计算：节拍r=计划期有效工作时间/计划期计算产量3.计算满足节拍需要的工作地的最小数量理论值。

S min=[工序时间之和/节拍]（最终结果进位取整）4.组织工作地。

按节拍要求分配组织各工作地的工序（在网络图上标）。

分配时要遵循：保证各工序之间的先后顺序；各工作地的作业时间应尽量接近或等于节拍；工作地数目尽量少。

5.评价装配平衡的效率：装配线的效率=完成作业所需时间/实际工作地数*节拍二、用代表产品法或假定产品法计算设备生产能力1.代表产品法的步骤：①选定代表产品。

因*产品计划产量（或计划产量与台时定额之积）最大，故选*产品为代表产品。

②计算换算系数。

见表中第③项。

（以代表产品的台时定额为分母，其它产品的台时定额为分子，计算每种产品的换算系数。

）（将每个产品的换算系数填入表格中）③计算表中第④项。

（用每种产品的计划产量乘换算系数，得出用代表产品表示的产量。

并填入表中。

）④计算产量比重。

见表中第⑤项。

每个产品的产量/总产量⑤计算生产能力：表中第⑥项设备生产能力=设备年有效工作小时数/代表产品台时定额 = **=年有效工作日*每天工作小时数*设备台数*（1-设备检修率）/代表产品台时定额（生产能力取整，小数部分只舍不入），结果填入表中。

⑥按产量比重计算各产品生产能力⑦=生产能力⑥*比重⑤/换算系数③，将各产品生产能力填入表中。

⑦如生产能力大于计划产量，则表示能力满足计划需求；•（或如生产能力小于计划产量，则表示生产能力不足，企业应想办法增加生产能力来满足需求。

）2.假定产品法的步骤：①计算假定产品台时定额。

③=（每种产品的计划产量与台时定额乘积的和/总产量）=①A*②A+①B*②B+①C*②C+①D*②D/总产量②计算产量比重。

见表中第④项。

每个产品的产量/总产量③计算设备生产能力=设备年有效工作小时数/代表产品台时定额 = **=年有效工作日*每天工作小时数*设备台数*（1-设备检修率）/代表产品台时定额（生产能力取整，小数部分只舍不入），结果填入表中。

运营管理有关装配线平衡案例及答案
1、什么是运营战略，以及它与企业战略的关系?
答:运营战略是指在企业战略的总体框架下，决定如何通过运作活动来达到企业整体目标的总体计划，为实现企业战略提供生产运营部门的行为路径。

关系:生产运营战略和企业战略呈一种相互依存和相互制约的关系。

一方面，公司级战略统领企业经营的全局，为企业的经营与发展确定目标，指明方向，而生产运营战略作为企业生产运营方面特定活动的行为纲领，必须和企业战略协调一致。

另一方面，通过生产运营战略等职能级战略，可以对企业战略进行分解，导出企业战略的途径和政策，将企业总体战略思想和目标加以精确化、具体化，规范人们的决策和行为标准，指导各方面的活动。

2、生产运作总体策略包括哪些内容?
答:生产运作的总体策略包括选择自制还是外包、产品结构和产业结构的选择、组织生产是预测驱动还是订单驱动、采用高效供应链还是敏捷供应链以及配送网络的选择。

3、生产运作系统设计有哪些重要决策?
答:生产运作系统的设计有四个方面的策略，即选址、设施布置、岗
位设计以及工作考核和报酬。

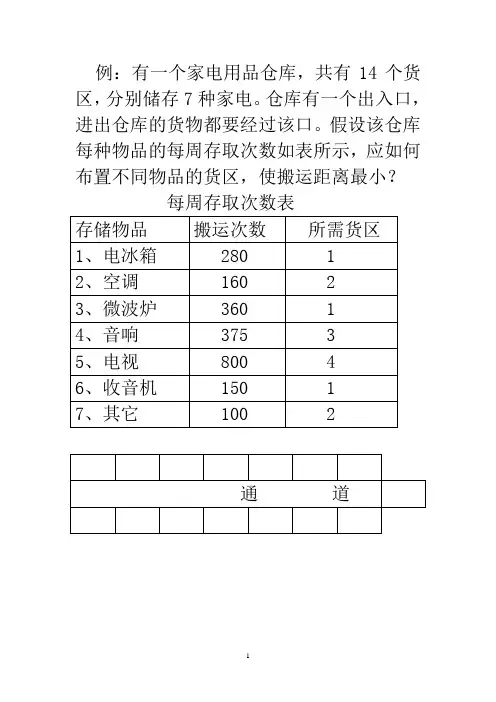
例：有一个家电用品仓库，共有14个货区，分别储存7种家电。

仓库有一个出入口，进出仓库的货物都要经过该口。

假设该仓库每种物品的每周存取次数如表所示，应如何布置不同物品的货区，使搬运距离最小？每周存取次数表4、生产线平衡步骤（1）用一个流程图表示作业先后关系（2）求出生产节拍 r = 计划期有效工作时间／计划期间计划产量 = Fe／N（3）计算满足节拍要求的最少工作地数S = 完成单件产品所需的总时间／节拍= ∑ti／r（4）将作业分配到各工作地（启发式分配规则）①从工作地1开始，从左向右给工作地分配作业。

②该工作地单件时间不超过工作地的剩余时间剩余时间 = 节拍—该工作地已分配作业单件时间之和③若干作业满足条件2a.分配后续作业数最多的作业b.分配加工时间最长的作业例1、一玩具要在一个传送带上组装，每天需生产500辆。

每天的生产时间为420分钟，下表中列出了玩具的组装步骤及其时间。

请（1）画出组装作业先后顺序图；（2）该组装线的节拍是多大；（3）求工作地最小数目。

玩具的组装步骤及其时间作业时间(秒) 紧前作业A 45 -B 11 AC 9 BD 50 -E 15 DF 12 CG 12 CH 12 EI 12 EJ 8 G,F,H,I K 6 J解：（1）画出流程图，表示作业先后关系FA BGD E H J KI（2）计算节拍节拍=每天的工作时间/每天的产量=420*60/500=50.4（秒/辆）（3）最小工作数目= 完成单件作业所需的总时间/节拍 =192/50.4=3.81最小工作地数目4个工作作作业剩余可安排的后续作业最时间最长地业时间时间紧后作业多的作业的作业1 A 45 5.4 无2 D 50 0.4 无3 B 11 39.4 C.E C .E EE 15 24.4 C.H. I CC 9 15.4 F.G.H.I F.G.H .I F.G.H.IF 12 3.4 无4 G 12 38.4 H .I H .I H.IH 12 26.4 II 12 14.4 JJ 8 6.4 KK 6 0.4 无例2. 一装配线计划每小时装配200件产品，每小时用于生产的时间是50分钟。

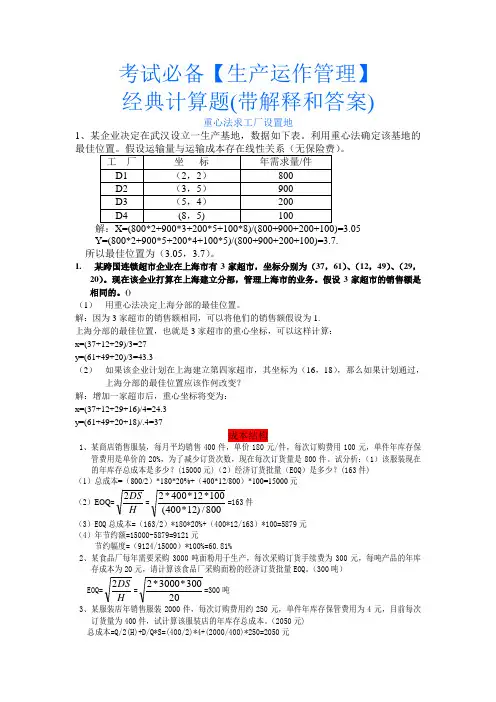
考试必备【生产运作管理】 经典计算题(带解释和答案)重心法求工厂设置地1、某企业决定在武汉设立一生产基地，数据如下表。

利用重心法确定该基地的最佳位置。

假设运输量与运输成本存在线性关系（无保险费）。

工 厂 坐 标 年需求量/件 D1 （2，2） 800 D2 （3，5） 900 D3 （5，4） 200 D4 (8，5) 100解：X=(800*2+900*3+200*5+100*8)/(800+900+200+100)=3.05 Y=(800*2+900*5+200*4+100*5)/(800+900+200+100)=3.7. 所以最佳位置为（3.05，3.7）。

1. 某跨国连锁超市企业在上海市有3家超市，坐标分别为（37，61）、（12，49）、（29，20）。

现在该企业打算在上海建立分部，管理上海市的业务。

假设3家超市的销售额是相同的。

()（1） 用重心法决定上海分部的最佳位置。

解：因为3家超市的销售额相同，可以将他们的销售额假设为1. 上海分部的最佳位置，也就是3家超市的重心坐标，可以这样计算： x=(37+12+29)/3=27 y=(61+49+20)/3=43.3（2） 如果该企业计划在上海建立第四家超市，其坐标为（16，18），那么如果计划通过，上海分部的最佳位置应该作何改变？解：增加一家超市后，重心坐标将变为： x=(37+12+29+16)/4=24.3 y=(61+49+20+18)/.4=37成本结构1、某商店销售服装，每月平均销售400件，单价180元/件，每次订购费用100元，单件年库存保管费用是单价的20%，为了减少订货次数，现在每次订货量是800件。

试分析：（1）该服装现在的年库存总成本是多少？(15000元)（2）经济订货批量（EOQ ）是多少？(163件) （1）总成本=（800/2）*180*20%+（400*12/800）*100=15000元 （2）EOQ =HDS 2=800/)12*400(100*12*400*2=163件（3）EOQ 总成本=（163/2）*180*20%+（400*12/163）*100=5879元（4）年节约额=15000-5879=9121元节约幅度=（9124/15000）*100%=60.81%2、某食品厂每年需要采购3000吨面粉用于生产，每次采购订货手续费为300元，每吨产品的年库存成本为20元，请计算该食品厂采购面粉的经济订货批量EOQ 。

产线平衡测试题
产线平衡测试题
请讲述你在工作中是如何做产线平衡的，具体的案例有哪些？（100分）
一、做产线平衡根据以下流程来制作：
1.例出产线工序并测试工时
2.计算节拍时间，
3.画工序流程图
4.决定瓶颈时间
5.确定理论工位数
6.制定工序流程
7.计算效率
二、相关案例有瓶子类、盖子类、口红类等等产品。

A.举例.如瓶子类以KK-082为例：
1.产线工序及工时如下：
2.计算节拍时间：a.假设客户需求量每天要生产15000PCS/天。

节拍时间CT=生产工作时间/生产量=10.5H*3600秒/15000PCS=2.52秒。

4.决定瓶颈时间：理论上工序中工时最长的为瓶颈，因客户需求CT为2.52秒，经过平衡后工序中瓶颈工时为2.5秒。

5.确定理论工位数=工序时间总和/节拍时间=24.5秒/2.52秒=9.72人—取整数10人。

6.制定工序流程
在确定工位数后，需要用到ECRS（删除、合并、重排、简化）来对工序进行调整，利用动作经济原则、IE七大手法来进行平衡改善。

运用这些工具来进行改善时需要考虑产品功能、产品质量、人员、机器、场地、物料等等来做改善。

8.计算效率
效率=工序时间总和/总人数*瓶颈工时=24.5秒/（10人*2.5秒）
=98%。

装配线平衡模型 一条装配线含有一系列的工作站，在最终产品的加工过程中每个工作站执行一种或几种特定的任务。

装配线周期是指所有工作站完成分配给它们各自的任务所化费时间中的最大值。

平衡装配线的目标是为每个工作站分配加工任务，尽可能使每个工作站执行相同数量的任务，其最终标准是装配线周期最短。

不适当的平衡装配线将会产生瓶颈——有较少任务的工作站将被迫等待其前面分配了较多任务的工作站。

问题会因为众多任务间存在优先关系而变得更复杂，任务的分配必须服从这种优先关系。

这个模型的目标是最小化装配线周期。

有2类约束： ① 要保证每件任务只能也必须分配至一个工作站来加工； ② 要保证满足任务间的所有优先关系。

例 有11件任务（A —K ）分配到4个工作站（1—4），任务的优先次序如下图。

每件任务所花费的时间如下表。

MODEL :!装配线平衡模型; SETS :!任务集合，有一个完成时间属性T; TASK/ A B C D E F G H I J K/: T; !任务之间的优先关系集合（A 必须完成才能开始B ，等等）; PRED( TASK, TASK)/ A,B B,C C,F C,G F,J G,J J,K D,E E,H E,I H,J I,J /; ! 工作站集合; STATION/1..4/; TXS( TASK, STATION): X; ! X 是派生集合TXS 的一个属性。

如果X （I ，K ）＝1，则表示第I 个任务 指派给第K 个工作站完成; ENDSETS DATA : !任务A B C D E F G H I J K 的完成时间估计如下; T = 45 11 9 50 15 12 12 12 12 8 9; ENDDATA! 当任务超过15个时，模型的求解将变得很慢; !每一个作业必须指派到一个工作站，即满足约束①; @FOR ( TASK( I): @SUM ( STATION( K): X( I, K)) = 1); !对于每一个存在优先关系的作业对来说，前者对应的工作站I 必须小于后者对应的工作站J ，即满足约束②; @FOR ( PRED( I, J): @SUM ( STATION( K): K * X( J, K) - K * X( I, K)) >= 0);!对于每一个工作站来说，其花费时间必须不大于装配线周期; @FOR ( STATION( K):@SUM ( TXS( I, K): T( I) * X( I, K)) <= CYCTIME);(A) (B) (C) (F) (G) (K) (J) (I) (H)(E)(D)!目标函数是最小化转配线周期;MIN = CYCTIME;!指定X(I,J) 为0/1变量;@FOR( TXS: @BIN( X));END计算的部分结果为Global optimal solution found at iteration: 1255Objective value: 50.00000Variable Value Reduced Cost CYCTIME 50.00000 0.000000 X( A, 1) 1.000000 0.000000 X( A, 2) 0.000000 0.000000 X( A, 3) 0.000000 45.00000 X( A, 4) 0.000000 0.000000 X( B, 1) 0.000000 0.000000 X( B, 2) 0.000000 0.000000 X( B, 3) 1.000000 11.00000 X( B, 4) 0.000000 0.000000 X( C, 1) 0.000000 0.000000 X( C, 2) 0.000000 0.000000 X( C, 3) 0.000000 9.000000 X( C, 4) 1.000000 0.000000 X( D, 1) 0.000000 0.000000 X( D, 2) 1.000000 0.000000 X( D, 3) 0.000000 50.00000 X( D, 4) 0.000000 0.000000 X( E, 1) 0.000000 0.000000 X( E, 2) 0.000000 0.000000 X( E, 3) 1.000000 15.00000 X( E, 4) 0.000000 0.000000 X( F, 1) 0.000000 0.000000 X( F, 2) 0.000000 0.000000 X( F, 3) 0.000000 12.00000 X( F, 4) 1.000000 0.000000 X( G, 1) 0.000000 0.000000 X( G, 2) 0.000000 0.000000 X( G, 3) 0.000000 12.00000 X( G, 4) 1.000000 0.000000 X( H, 1) 0.000000 0.000000 X( H, 2) 0.000000 0.000000 X( H, 3) 1.000000 12.00000 X( H, 4) 0.000000 0.000000 X( I, 1) 0.000000 0.000000 X( I, 2) 0.000000 0.000000 X( I, 3) 1.000000 12.00000 X( I, 4) 0.000000 0.000000 X( J, 1) 0.000000 0.000000 X( J, 2) 0.000000 0.000000 X( J, 3) 0.000000 8.000000X( J, 4) 1.000000 0.000000X( K, 1) 0.000000 0.000000X( K, 2) 0.000000 0.000000X( K, 3) 0.000000 9.000000X( K, 4) 1.000000 0.000000二次分配问题（Quadratic Assignment Problem ）这个问题是指派问题的一种推广。