29 。2三视图导学单(1)

三视图（一）教学设计一、学习目标1、会从投影的角度理解视图的概念2、会画简单几何体的三视图3、培养实践动手能力，发展空间想象能力二、教学重、难点重点：从投影的角度加深对三视图的理解和会画简单的三视图难点：对三视图概念理解及画简单的三视图三、学习过程（一）温故知新什么是投影？什么是正投影？（二）创设情境，引入新课1.我们看在一次军事演习中展示了各种飞机图案，（聪明的同学,你发现了吗?我们总是从哪几个角度来展示的.）学生自己总结教师总结：在生活中我们应从不同角度，多方面地去看待一件事物，分析一件事情。

但是在数学中我们只从三个不同方向看同一物体，所以，每一个物体都有三视图。

2、物体的正投影从一个方向反映了物体的形状和大小，为了全面地反映一个物体的形状和大小，我们常常再选择正面和侧面两个投影面，画出物体的正投影。

如图(1)，我们用三个互相垂直的平面作为投影面，正对着我们的叫做正面，正面下方的叫做水平面，右边的叫做侧面.一个物体(例如一个长方体)在三个投影面内同时进行正投影，在正面内得到的由前向后观察物体的视图，叫做主视图，在水平面内得到的由上向下观察物体的视图，叫做俯视图;在侧面内得到由左向右观察物体的视图，叫做左视图.如图(2)，将三个投影面展开在一个平面内，得到这一物体的一张三视图(由主视图，俯视图和左视图组成).三视图中的各视图，分别从不同方面表示物体，三者合起来就能够较全面地反映物体的形状.三视图中，主视图与俯视图表示同一物体的长，主视图与左视图表示同一物体的高.左视图与俯视图表示同一物的宽，因此三个视图的大小是互相联系的.画三视图时.三个视图要放在正确的位置.并且使主视图与俯视图的长对正，主视图与左视图的高平齐.左视图俯视图的宽相等通过以上的学习，你有什么发现？ (三)探究三视图的特征： 1、物体的三视图实际上是物体在三个不同方向的正投影.正投影面上的正投影就是主视图，水平投影面上的正投影就是俯视图，侧投影面上的正投影就是左视图2、长对正、高平齐3、宽相等主视图左视图俯视图从左面看(四)拓展延伸提升能力1.、画出如图所示四棱锥的三视图。

三视图复习导学案姓名班级K教学目标X1、知识与技能：能识别简单物体的三视图，了解各个视图之间的尺寸关系；长对正、高平齐、宽相等.会画棱柱与圆柱等简单组合体的三视图.2、过程与方法：感受从不同方向观察同一物体可能看到不一样的结果，培养学生全面观察的能力.3、情感态度与价值观：培养学生自主学习与合作的学习方式K教学重点与难点X♦教学重点：补画三视图中缺线♦教学难点：补画三视图中缺线.K基础知识回顾X1.一般技术图样所采用的投影方法是正投影法，假设投影线与投影平面垂直。

为了确定物体的结构形状，需要采用多面正投影，一般采用三投影面体系(V—,H-,W-)2.简单形体的三视图(一)三视图形成(1)主视图：物体的正面投影，物体由向投影所得的图形，反映物体的,反映物体的和:(2)俯视图，物体的水平投影，物体由向投影所得的图形，反映物体的和:⑶左视图，物体的投影，物体由向投影所得的图形，反映物体的和。

(二)三视图投影规律：主视图与俯视图*3主视图与左视图：I俯视图与左视图：。

主视图左视图俯视图(三)三视图的空间方位关系主视图的上、下、左、俯视图的上、下、左、左视图的上、下、左、（四）三视图的线型绘制可见轮廓线用— 右：对应物体的上、下、左、右 右：对应物体的 ____ 、 _____ 、左、右 右：对应物体的上、下、 _____ 、 ____ 一线；绘制不可见轮廓线用 ________ 线; 绘制对称中心线或轴线用 ______ 线；绘制辅助1K 典型例题X1、根据立体图分步骤画出三视图心 2、根据三视图说明该结构是由 _______________Fl Ue 3、看懂三视图、补画出所缺的线 K 课堂随练》 看懂三视图、补画出所缺的线 QKXl M v 线用 ______ 线。

演变形成 G1.三 4G >I -O 3 IM11/u hς I: 11JK补充知识:X按照直线对三个投影面的相对位置，可以把直线分为三类：一般位置直线、投影面平行线、投影面垂直线。

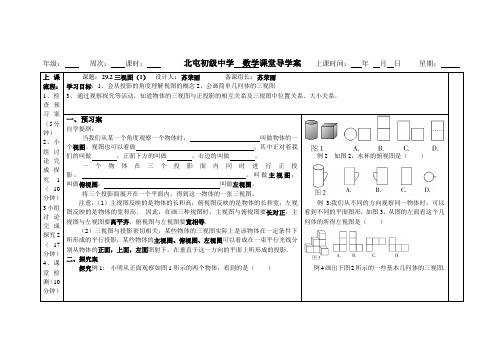
三视图课题： 29.2三视图（1）序号：学习目标：1、知识和技能：会从投影角度理解视图的概念。

会画简单几何体的三视图。

2、过程和方法：通过具体活动，积累观察，想象物体投影的经验。

培养学生自主学习与合作学习相结合的学习方式，使学生体会从生活中发现数学。

3、情感、态度、价值观：在应用数学解决生活中问题的过程中，品尝成功的喜悦，激发学生应用数学的热情。

学习重点：从投影的角度加深对三视图概念的理解。

会画简单几何体的三视图。

学习难点：对三视图概念理解的升华。

正确画出三棱柱的三视图和小零件的三视图。

导学方法：课时：导学过程一、课前预习：预习课本第P108——110的有关内容，尝试完成《导学案》的教材导读和自主测评。

二、课堂导学：1、导入还记得苏轼的《题西林壁》这首诗吗？它告诉我们从不同的方向看同一物体时，看到的图象可能不一样？这节课我们就来学习从不同的方向看物体。

2、出示任务自主学习阅读课本第P108——110的有关内容，尝试回答下列问题：什么叫视图？什么是三视图?三视图包括哪些视图？学习三视图的意义是什么？三视图的位置有什么规定？5）画三视图时我们应注意什么？6）阅读例1，反思三视图的具体画法，你还知道哪些几何体的三视图？(三视图取决于物体的摆放位置) 3、合作探究见《导学》P115难点探究三、反馈与反馈：检查自学情况，解释学生疑惑。

四、学习小结：1、视图：从某一角度观察一个物体时，所得到的图象叫做物体的一个视图。

2、三视图的定义3、三视图的位置规定4、三视图的具体画法画这些基本几何体的三视图时，要注意从三个方面观察它们.具体画法为:.确定三视图的位置，画出主视图;.在主视图正下方画出俯视图，注意与主视图“长对正”。

.在主视图正右方画出左视图.注意与主视图“高平齐”，与俯视图“宽相等”.五、达标检测1、课后练习2、《导学案》自主测评3、画出图中的几何体的三视图。

题后小结：画三视图时，看得见的轮廓线通常画成实线，看不见的部分通常画成虚线。

三视图导学稿九年级数学下册第29章导学稿课题29.2三视图审核人级部审核学习时间第15周第4导学稿教师寄语今日事，今日毕。

不要把今天的事拖到明天。

学习目标1、学会根据物体的三视图描述出几何体的基本形状或实物原型；经历探索简单的几何体的三视图的还原，进一步发展空间想象能力。

由三视图进行简单几何体的有关计算学习重点根据物体的三视图描述出几何体的基本形状或实物原型学习难点学生空间想象能力的培养．学生自主活动材料一、前置自学球体的三种视图是A.三个圆B.两个圆和一个长方形c.两个圆和一个半圆 D.一个圆和两个半圆如右图是某几何体的三种视图，则该几何体是A.正方体B.圆锥体c.圆柱体D.球体如果一个立体图形的主视图为矩形，则这个立体图形可能是。

二、合作探究一个几何体的三视图如图所示，它的俯视图为菱形．请写出该几何体的形状，并根据图中所给的数据求出它的侧面积。

三、拓展提升圆柱的左视图是，俯视图是. 、如果一个几何体的主视图、左视图与俯视图都是一样的图形，那么这个几何体可能是＿＿.一个圆柱的轴截面平行于投影面,圆柱的正投影是一个边长为10的正方形,求圆柱的体积和表面积.四、当堂反馈一个物体的三视图如右图所示，该物体是A.圆柱B.圆锥c.棱锥D.棱柱如图，上下底面为全等的正六边形礼盒，其正视图与左视图均由矩形构成，正视图中大矩形边长如图所示，侧视图中包含两全等的矩形，如果用彩色胶带如图包扎礼盒，所需胶带长度至少为A．320cB．395.24cc．431.76cD．480c如图是由一些完全相同的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用的小立方块的个数是A.5个B.6个c.7个D.8个一个几何体的三视图如图所，则这个几何体的体积是．长方体的主视图与左视图如图所示，则其俯视图的面积是多少？。

《三视图》导学案一、学习目标1、了解三视图的概念，掌握三视图的形成原理。

2、能够画出简单几何体的三视图，并且能根据三视图还原几何体。

3、通过三视图的学习，培养空间想象能力和几何直观能力。

二、学习重难点1、重点（1）三视图的概念和形成原理。

（2）简单几何体三视图的画法。

2、难点（1）根据三视图还原几何体。

（2）理解三视图中各视图之间的关系。

三、知识链接1、回顾立体几何中常见的几何体，如正方体、长方体、圆柱、圆锥、球等。

2、思考从不同角度观察物体所看到的形状可能不同。

四、学习过程（一）三视图的概念1、观察思考观察身边的物体，如文具盒、水杯等，从不同的角度观察，你看到的形状一样吗？2、引入概念我们从正前方、正上方、正左方观察一个物体时，所得到的平面图形叫做这个物体的三视图。

3、三视图的名称（1）主视图：从物体的正前方得到的视图。

（2）俯视图：从物体的正上方得到的视图。

（3）左视图：从物体的正左方得到的视图。

（二）三视图的形成原理1、以长方体为例将长方体放在水平面上，分别从正前方、正上方、正左方观察。

2、正投影光线垂直于投影面时的投影叫做正投影。

3、三视图的形成（1）主视图：将长方体正对着我们，光线从正前方垂直照射，在投影面上得到的正投影就是主视图。

（2）俯视图：光线从正上方垂直照射，在水平面上得到的正投影就是俯视图。

（3）左视图：光线从正左方垂直照射，在竖直面上得到的正投影就是左视图。

（三）三视图的位置关系和大小关系1、位置关系（1）主视图在上方，俯视图在主视图的正下方，左视图在主视图的正右方。

（2）俯视图和左视图的宽度相等，主视图和俯视图的长度相等，主视图和左视图的高度相等。

2、大小关系（1）主视图反映物体的长和高。

（2）俯视图反映物体的长和宽。

（3）左视图反映物体的宽和高。

（四）简单几何体三视图的画法1、圆柱（1）主视图：是一个长方形，长方形的长等于圆柱的底面直径，长方形的宽等于圆柱的高。

（2）俯视图：是一个圆，圆的直径等于圆柱的底面直径。

第二十九章投影与视图§29.2三视图——第一课时（P94-P97）一、自主探究（看书理解、记忆，把重点知识句划在书上，并把课后简单练习完成在书上）1.回顾： ________________________________ 叫正投影.2•当我们从某一个角度观察一个物体时，______________________ 叫做物体的一个视图.视图也可以看做___________________ .其中正对着我们的叫做__________ ，正面下方的叫做 ________ ，右边的叫做___________ .3._______________________________________________________ —个物体在三个投影面内同时进行正投影，_____________________________________ ，叫做主视图；叫做俯视图； _______________ 叫做左视图.4.将三个投影面展开在一个平面内，得到这一物体的一张三视图.注意：（1）主视图反映的是物体的长和高；俯视图反映的是物体的长和宽；左视图反映的是物体的宽和高. 因此，在画三种视图时，主视图与俯视图要长对正，主视图与左视图要高平齐，俯视图与左视图要宽相等.（2）三视图与投影密切相关，某些物体的三视图实际上是该物体在一定条件下所形成的平行投影，某些物体的主视图、俯视图、左视图可以看成在一束平行光线分别从物体的正面，上面，左面照射下，在垂直于这一方向的平面上所形成的投影•、合作探究（自主学习时完成，课上交流展示）1•小明从正面观察如图1所示的两个物体，看到的是（）23OD—U图L D.2.如图2,水杯的俯视图是（）W23.我们从不同的方向观察同一物体时,的左面看这个几何体的所得左视图是（可以看到不同的平面图形, 如图3,从图、探究应用（课上完成并交流展示） 例1.画出右图所示的一些基本几何体的三视图 解:例2.画出如图所示的支架（一种小零件）的三视图•支架的两个台阶的高度和宽度 都是同一长度出它的三视图解：（补充）例•右图是一根钢管的直观图，画出它的三视图解：总结：基本几何体包括圆柱、圆锥、球、直棱柱、圆台，它们的三视图是画复杂 几何体三视图的基础•基本几何体的三视图：（1） 正方体的三视图都是正方形.（2） 圆柱的三视图中有两个是长方形，另一个是圆 .B.C. D.(3)圆锥的三视图中有两个是三角形，另一个是圆和一个点.(4)四棱锥的三视图中有两个是三角形，另一个是矩形和它的对角线(5)球体的三视图都是圆形.四、巩固再现：P97练习五、能力提升：1.右图是由几个小立方块搭成的几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，那么这个几何体的主视图是(2.如图所示，画出该物体的三视图六、探究小结：1•你学会了什么？ ____________________________________________________________2.你存在的问题？____________________________________________________________。

29.2三视图（第一课时）【学习目标】（一）知识技能：1.会从投影角度理解视图的概念。

2.会画简单几何体的三视图。

（二）数学思考：通过具体活动，积累观察，想象物体投影的经验。

（三）解决问题：会画实际生活中简单物体的三视图。

（四）情感态度：1.培养学生自主学习与合作学习相结合的学习方式，使学生体会从生活中发现数学。

2.在应用数学解决生活中问题的过程中，品尝成功的喜悦，激发学生应用数学的热情。

【学习重点】1.从投影的角度加深对三视图概念的理解。

2.会画简单几何体的三视图。

【学习难点】1.对三视图概念理解的升华。

2.正确画出三棱柱的三视图和小零件的三视图。

【学习过程】【情境引入】活动一如图，直三棱柱的侧棱与水平投影面垂直。

请与同伴一起探讨下面的问题：（1）以水平投影面为投影面，在正投影下，这个直棱柱的三条侧棱的投影是什么图形？（2）画出直三棱柱在水平投影面的正投影，得到的投影是什么图形？它与直三棱柱的底面有什么关系？（3）这个水平投影能完全反映这个物体的形状和大小吗？如不能，那么还需哪些投影面？【自主探究】活动二学生观察思考：（1）三个视图位置上的关系。

（2）三个视图除了位置上的关系，在大小尺寸上，彼此之间又存在什么关系？小结：1.三视图位置有规定，主视图要在，俯视图应在，左视图要在。

2.三视图中各视图的大小也有关系。

主视图与俯视图表示同一物体的，主视图与左视图表示同一物体的，左视图与俯视图表示同一物体的。

因此三视图的大小是互相联系的。

画三视图时，三个视图要放在正确的位置，并且使主视图与俯视图的，主视图与左视图的，左视图与俯视图的。

活动三例1 画出下图2所示的一些基本几何体的三视图.题后小结:画这些基本几何体的三视图时，要注意从个方面观察它们.具体画法为:1.确定视图的位置，画出视图;2.在视图正下方画出视图，注意与主视图“”。

3.在视图正右方画出视图.注意与主视图“”，与俯视图“”.【巩固练习】1.画出图中的几何体的三视图。

教学设计内容及流程教师与学生活动备注实施目标二、自主预习梳理新知1.三视图位置有规定，主视图要在，俯视图应在，左视图要在。

2.三视图中各视图的大小也有关系。

主视图与俯视图表示同一物体的，主视图与左视图表示同一物体的，左视图与俯视图表示同一物体的。

因此三视图的大小是互相联系的。

画三视图时，三个视图要放在正确的位置，并且使主视图与俯视图的，主视图与左视图的，左视图与俯视图的。

三、合作探究生成能力目标导学一：简单几何体的三视图活动：如图，直三棱柱的侧棱与水平投影面垂直。

请与同伴一起探讨下面的问题：（1）以水平投影面为投影面，在正投影下，这个直棱柱的三条侧棱的投影是什么图形？（2）画出直三棱柱在水平投影面的正投影，得到的投影是什么图形？它与直三棱柱的底面有什么关系？（3）这个水平投影能完全反映这个物体的形状和大小吗？如不能，那么还需哪些投影面？师生共同总结：我们用三个互相垂直的平面（例如墙角处的三面墙壁）作为投影面．其中正对着我们的叫做正面．正面下方的叫做水平面，右边的叫做侧面．一个物体在三个投影面内同时进行正投影，在正面内得到的由前向后观察物体的视图，叫做主视图；在水平面内得到的由上向下观察物体的视图，叫做俯视图；在侧面内得到由左向右观察物体的视图，叫做左视图。

例1：下面的几何体中，俯视图为三角形的是()解析：选项A.长方体的俯视图是长方形，错误；选项B.圆锥的俯视图是带圆心的圆，错误；选项C.圆柱的俯视图是圆，错误；选项D.三棱柱的俯视图是三角形，正确；故选D.目标导学二：画图形的三视图例2：分别画出图中几何体的主视图、左视图和俯视图．解析：从正面看，从左往右4列正方形的个数依次为1，3，1，1；从左面看，从左往右3列正方形的个数依次为3，1，1；从上面看，从左往右4列正方形的个数依次为1，3，1，1.解：如图所示：方法总结：画三视图的步骤：①确定主视图位置，画出主视图；②在主视图的正下方画出俯视图，注意与主视图“长对正”；③在主视图的正右方画出左视图，注意与主视图“高平齐”、与俯视图“宽相等”．要注意几何体看得见部分的轮廓线画成实线，被其他部分遮挡而看不见的部分的轮廓线画成虚线．目标导学三：由三视图确定几何体例3：一个几何体的三视图如图所示，则这个几何体是()A．四棱锥B．四棱柱C．三棱锥D．三棱柱解析：主视图是由两个矩形组成，而左视图是一个矩形，俯视图是一个三角形，得出该几何体是一个三棱柱．故选D.方法总结：由三视图想象几何体的形状，首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．四、课堂总结大家课下要选用适当的实物，把几何体与三视图有机结合。

29.2 视图（第二课时）导学案1.进一步认识由物体画视图、由视图想象物体；2.会初步利用三视图画出简单立体图形；3.会利用三视图计算立体图形的侧面积和表面积；4.通过观察、探究等活动，先让学生由物体的三视图想象出物体的形状，再由物体的形状进一步画出展开图.★知识点1：已知三视图想象立体图形的方法：由三视图想象立体图形时，先分别根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状，然后再综合起来考虑整体图形．再根据三视图“长对正、高平齐、宽相等”的关系，确定轮廓线的位置以及各个方向的尺寸.★知识点2：由三视图求立体图形的面积（体积）的方法：1）先根据给出的三视图确定立体图形，并确定立体图形的长、宽、高.2）将立体图形展开成一个平面图形 (展开图)，观察它的组成部分.3）最后根据已知数据，求出展开图的面积（体积）.一、已知三视图想象立体图形的方法：由三视图想象立体图形时，先分别根据主视图、俯视图和左视图想象立体图形的________、________和___________的局部形状，然后再综合起来考虑__________．再根据三视图“_____对正、_________平齐、______相等”的关系，确定轮廓线的_______以及各个方向的___________.二、由三视图求立体图形的面积（体积）的方法：1）先根据给出的三视图确定立体图形，并确定立体图形的_______________.2）将立体图形展开成一个_________________，观察它的组成部分.3）最后根据已知数据，求出展开图的面积（体积）.【提问一】简述被观察物体三视图之间的关系？【提问二】简述画三视图的具体方法？【新课引入】前面我们讨论了由立体图形（实物）画出三视图，下面我们讨论由三视图想象出立体图形（实物）．【问题一】如图，分别根据三视图(1) (2)说出立体图形的名称.例1 根据物体的三视图描述物体的形状.【针对训练】1.根据物体的三视图描述物体的形状.某工厂要加工一批密封罐，设计者给出了密封罐的三视图，请你按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位：mm)。