通用技术三视图导学案

三视图（一）教学设计一、学习目标1、会从投影的角度理解视图的概念2、会画简单几何体的三视图3、培养实践动手能力，发展空间想象能力二、教学重、难点重点：从投影的角度加深对三视图的理解和会画简单的三视图难点：对三视图概念理解及画简单的三视图三、学习过程（一）温故知新什么是投影？什么是正投影？（二）创设情境，引入新课1.我们看在一次军事演习中展示了各种飞机图案，（聪明的同学,你发现了吗?我们总是从哪几个角度来展示的.）学生自己总结教师总结：在生活中我们应从不同角度，多方面地去看待一件事物，分析一件事情。

但是在数学中我们只从三个不同方向看同一物体，所以，每一个物体都有三视图。

2、物体的正投影从一个方向反映了物体的形状和大小，为了全面地反映一个物体的形状和大小，我们常常再选择正面和侧面两个投影面，画出物体的正投影。

如图(1)，我们用三个互相垂直的平面作为投影面，正对着我们的叫做正面，正面下方的叫做水平面，右边的叫做侧面.一个物体(例如一个长方体)在三个投影面内同时进行正投影，在正面内得到的由前向后观察物体的视图，叫做主视图，在水平面内得到的由上向下观察物体的视图，叫做俯视图;在侧面内得到由左向右观察物体的视图，叫做左视图.如图(2)，将三个投影面展开在一个平面内，得到这一物体的一张三视图(由主视图，俯视图和左视图组成).三视图中的各视图，分别从不同方面表示物体，三者合起来就能够较全面地反映物体的形状.三视图中，主视图与俯视图表示同一物体的长，主视图与左视图表示同一物体的高.左视图与俯视图表示同一物的宽，因此三个视图的大小是互相联系的.画三视图时.三个视图要放在正确的位置.并且使主视图与俯视图的长对正，主视图与左视图的高平齐.左视图俯视图的宽相等通过以上的学习，你有什么发现？ (三)探究三视图的特征： 1、物体的三视图实际上是物体在三个不同方向的正投影.正投影面上的正投影就是主视图，水平投影面上的正投影就是俯视图，侧投影面上的正投影就是左视图2、长对正、高平齐3、宽相等主视图左视图俯视图从左面看(四)拓展延伸提升能力1.、画出如图所示四棱锥的三视图。

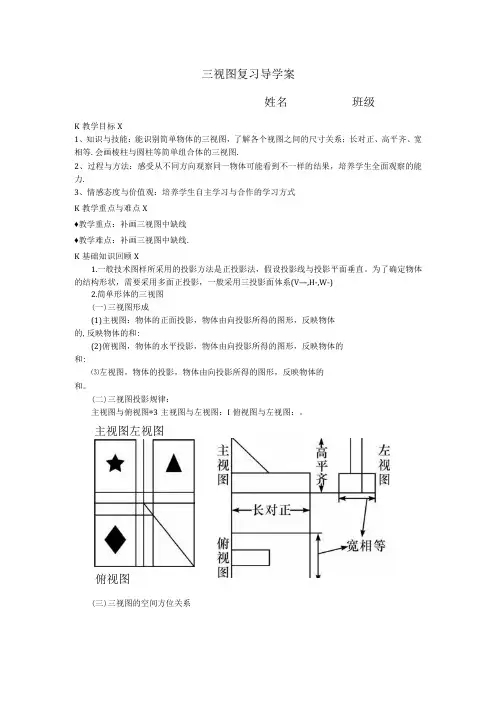
三视图复习导学案姓名班级K教学目标X1、知识与技能：能识别简单物体的三视图，了解各个视图之间的尺寸关系；长对正、高平齐、宽相等.会画棱柱与圆柱等简单组合体的三视图.2、过程与方法：感受从不同方向观察同一物体可能看到不一样的结果，培养学生全面观察的能力.3、情感态度与价值观：培养学生自主学习与合作的学习方式K教学重点与难点X♦教学重点：补画三视图中缺线♦教学难点：补画三视图中缺线.K基础知识回顾X1.一般技术图样所采用的投影方法是正投影法，假设投影线与投影平面垂直。

为了确定物体的结构形状，需要采用多面正投影，一般采用三投影面体系(V—,H-,W-)2.简单形体的三视图(一)三视图形成(1)主视图：物体的正面投影，物体由向投影所得的图形，反映物体的,反映物体的和:(2)俯视图，物体的水平投影，物体由向投影所得的图形，反映物体的和:⑶左视图，物体的投影，物体由向投影所得的图形，反映物体的和。

(二)三视图投影规律：主视图与俯视图*3主视图与左视图：I俯视图与左视图：。

主视图左视图俯视图(三)三视图的空间方位关系主视图的上、下、左、俯视图的上、下、左、左视图的上、下、左、（四）三视图的线型绘制可见轮廓线用— 右：对应物体的上、下、左、右 右：对应物体的 ____ 、 _____ 、左、右 右：对应物体的上、下、 _____ 、 ____ 一线；绘制不可见轮廓线用 ________ 线; 绘制对称中心线或轴线用 ______ 线；绘制辅助1K 典型例题X1、根据立体图分步骤画出三视图心 2、根据三视图说明该结构是由 _______________Fl Ue 3、看懂三视图、补画出所缺的线 K 课堂随练》 看懂三视图、补画出所缺的线 QKXl M v 线用 ______ 线。

演变形成 G1.三 4G >I -O 3 IM11/u hς I: 11JK补充知识:X按照直线对三个投影面的相对位置，可以把直线分为三类：一般位置直线、投影面平行线、投影面垂直线。

29.2三视图3【教学内容】课本99—100页内容。

【教学目标】知识与技能1、学会根据物体的三视图描述出几何体的基本形状或实物原型。

2、经历探索简单的几何体的三视图的还原，进一步发展空间想象能力。

3、了解将三视图转换成立体图形在生产中的作用，使学生体会到所学知识有重要的实用价值。

过程与方法经历简单的几何三视图的还原及体积和面积的计算，进一步发展学生的空间想象能力。

情感、态度与价值观使学生学会全面认识事物，而不能片面的理解、分析问题。

【教学重难点】重点：根据三视图描述基本几何体和实物原型及三视图在生产中的作用。

难点：根据三视图想象基本几何体实物原型。

【导学过程】【知识回顾】根据三视图描述物体的形状【情景导入】前面我们讨论了由立体图形（实物）画出三视图，下面我们讨论由三视图想象出立体图形（实物）．并计算出它的表面积。

【新知探究】探究一、例6某工厂要加工一批密封罐，设计者给出了密封罐的三视图，请你按照三视图确定制作每个密封罐所需钢板的面积。

问题：要想救出每个密封罐所需钢板的面积，应先解决哪些问题？小组讨论结论：1、应先由三视图想象出物体的；2、画出物体的;解：该物体是：画出它的展开图是：它的表面积是：…….【知识梳理】本节课你学习了什么知识？【随堂练习】1、如图，上下底面为全等的正六边形的礼盒，其主视图与左视图均由矩形构成，主视图中大矩形的边长如图所示，左视图中包含两个全等的矩形。

如果用彩色胶带如图包扎礼盒，所需胶带长度至少为（）A、120cmB、395.24cmC、431.76cmD、480cm2、在一仓库里堆放着若干相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来。

如图所示，则这堆正方体货箱共有箱。

3、如图是一个由若干个棱长相等的正方体构成的几何体的三视图。

（1）请写出构成这个几何体的正方体的个数；（2）请根据图中所示的尺寸，计算这个几何体的表面积。

设计的表达与交流
学习目标：
1、理解三视图的形成原理
2、学会看三视图的各个部分对应关系
3、学会画简单的三视图
学习重点：三视图的识读
简单三视图的绘画
学习难点：三视图形成原理的理解一、概念介绍
1、三投影面体系：用三个互相垂直相交的平
面，构成三投影面体系
2、主视图：由前向后投影，在正面V上的视图
俯视图：由上向下投影，在水平面H上的视图
左视图：由左向右投影，在侧面W上的视图
任务一：超前体验
正立投影面V，水平投影面H,侧立投影面W..
三视图学案
试着画一画这几个常见的几何体的三个视图
■ ▲
任务二：达标训练
画一画这些图形的三视图是怎样的？
任务三、扩展练习
空间想象：
下面是一些立体图形的三视图，请根据视图说出立体图形的名
1、 on 3
、
交流探讨：三个视图是如何到一个平面上来的，有什么样的对应关系
4、教材76页技术实习练习题（注意对应关系）
A、连线
E、找出书上的错误点并改正
画三视图的简单方法，在零件上取个三投影面体系，从而确定主视图
任务四、提高标准：画出下列几何体的主视图、左视图和俯视图
1、
思考题：
1、图所示的两幅图分别是由几个小立方块搭成的几何体的俯视图，小正方形中 的数字表示该位置小立方块的个数请画出相应的主视图和左视图。

(2) 反思领悟：
本节课我学会了什么?
(1)。

《三视图》导学案一、学习目标1、了解三视图的概念，掌握三视图的形成原理。

2、能够画出简单几何体的三视图，并且能根据三视图还原几何体。

3、通过三视图的学习，培养空间想象能力和几何直观能力。

二、学习重难点1、重点（1）三视图的概念和形成原理。

（2）简单几何体三视图的画法。

2、难点（1）根据三视图还原几何体。

（2）理解三视图中各视图之间的关系。

三、知识链接1、回顾立体几何中常见的几何体，如正方体、长方体、圆柱、圆锥、球等。

2、思考从不同角度观察物体所看到的形状可能不同。

四、学习过程（一）三视图的概念1、观察思考观察身边的物体，如文具盒、水杯等，从不同的角度观察，你看到的形状一样吗？2、引入概念我们从正前方、正上方、正左方观察一个物体时，所得到的平面图形叫做这个物体的三视图。

3、三视图的名称（1）主视图：从物体的正前方得到的视图。

（2）俯视图：从物体的正上方得到的视图。

（3）左视图：从物体的正左方得到的视图。

（二）三视图的形成原理1、以长方体为例将长方体放在水平面上，分别从正前方、正上方、正左方观察。

2、正投影光线垂直于投影面时的投影叫做正投影。

3、三视图的形成（1）主视图：将长方体正对着我们，光线从正前方垂直照射，在投影面上得到的正投影就是主视图。

（2）俯视图：光线从正上方垂直照射，在水平面上得到的正投影就是俯视图。

（3）左视图：光线从正左方垂直照射，在竖直面上得到的正投影就是左视图。

（三）三视图的位置关系和大小关系1、位置关系（1）主视图在上方，俯视图在主视图的正下方，左视图在主视图的正右方。

（2）俯视图和左视图的宽度相等，主视图和俯视图的长度相等，主视图和左视图的高度相等。

2、大小关系（1）主视图反映物体的长和高。

（2）俯视图反映物体的长和宽。

（3）左视图反映物体的宽和高。

（四）简单几何体三视图的画法1、圆柱（1）主视图：是一个长方形，长方形的长等于圆柱的底面直径，长方形的宽等于圆柱的高。

（2）俯视图：是一个圆，圆的直径等于圆柱的底面直径。

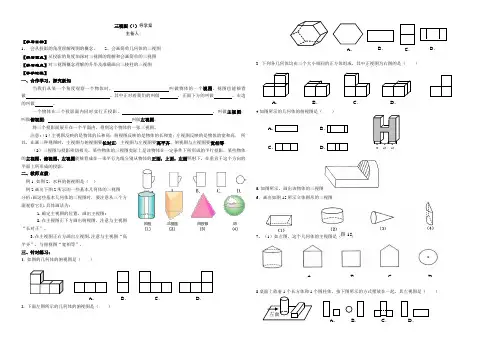
左面A ．B ．C ．D ．三视图（1）导学案主备人:【学习目标】1、 会从投影的角度理解视图的概念。

2、会画简单几何体的三视图 【学习重点】从投影的角度加深对三视图的理解和会画简单的三视图 【学习难点】对三视图概念理解的升华及准确画出三棱柱的三视图 【导学过程】一、合作学习，探究新知当我们从某一个角度观察一个物体时， 叫做物体的一个视图。

视图也能够看做 。

其中正对着我们的叫做 ，正面下方的叫做 ，右边的叫做 。

一个物体在三个投影面内同时实行正投影， ，叫做主视图； 叫做俯视图； 叫做左视图。

将三个投影面展开在一个平面内，得到这个物体的一张三视图。

注意:（1）主视图反映的是物体的长和高；俯视图反映的是物体的长和宽；左视图反映的是物体的宽和高． 所以，在画三种视图时，主视图与俯视图要长对正，主视图与左视图要高平齐，俯视图与左视图要宽相等．（2）三视图与投影密切相关，某些物体的三视图实际上是该物体在一定条件下所形成的平行投影，某些物体的主视图、俯视图、左视图能够看成在一束平行光线分别从物体的正面，上面，左面照射下，在垂直于这个方向的平面上所形成的投影。

二、教师点拨:例1 如图2，水杯的俯视图是（ ）例2画出下图2所示的一些基本几何体的三视图. 分析:画这些基本几何体的三视图时，要注意从三个方面观察它们.具体画法为:1.确定主视图的位置，画出主视图;2.在主视图正下方画出俯视图，注意与主视图“长对正”。

3.在主视图正右方画出左视图.注意与主视图“高平齐”，与俯视图“宽相等”. 三、针对练习：1. 如图的几何体的俯视图是（ ）2. 下面左图所示的几何体的俯视图是（ ）3. 下列各几何体均由三个大小相同的正方体组成，其中正视图．．．为右图的是（ ）4.如图所示的几何体的俯视图是（ ）5.如图所示，画出该物体的三视图6．画出如图15所示立体图形的三视图.7、（1）如左图，这个几何体的主视图是（ ）8.桌面上放着1个长方体和1个圆柱体，按下图所示的方式摆放在一起，其左视图是（ ）A ．B ．C ．D ．A ．B ．C ．D ．A ．B ．C ．D ．A ．B ．C ．D ．a a a图15A ．B ．C ．D ．。

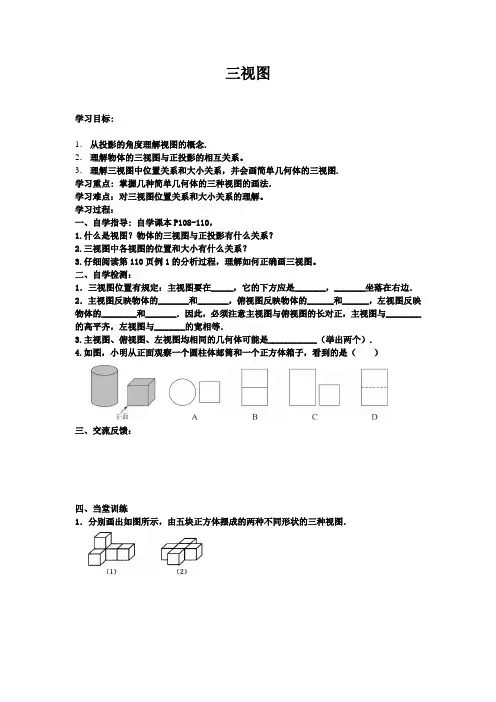
三视图学习目标:1．从投影的角度理解视图的概念.2．理解物体的三视图与正投影的相互关系。

3．理解三视图中位置关系和大小关系，并会画简单几何体的三视图.学习重点: 掌握几种简单几何体的三种视图的画法．学习难点：对三视图位置关系和大小关系的理解。

学习过程：一、自学指导: 自学课本P108-110，1.什么是视图？物体的三视图与正投影有什么关系？2.三视图中各视图的位置和大小有什么关系？3.仔细阅读第110页例1的分析过程，理解如何正确画三视图。

二、自学检测：1．三视图位置有规定：主视图要在_____，它的下方应是_______，_______坐落在右边．2．主视图反映物体的_______和_______，俯视图反映物体的______和______，左视图反映物体的________和_______．因此，必须注意主视图与俯视图的长对正，主视图与________的高平齐，左视图与_______的宽相等．3.主视图、俯视图、左视图均相同的几何体可能是___________（举出两个）.4.如图，小明从正面观察一个圆柱体邮筒和一个正方体箱子，看到的是（）三、交流反馈：四、当堂训练1．分别画出如图所示，由五块正方体摆成的两种不同形状的三种视图．1． 探索较为复杂的几何体的三视图画法。

2． 学会画较为复杂的几何体的三视图.学习重点: 会分析几何体的组成画出三视图。

学习难点：明确三视图中虚线和实线的区别。

学习过程：一、自学指导: 自学课本P111-112，1.思考课本图29．2-6中的支架可以看成哪些几何体组合而成的？三视图中为什么出现实线？2.思考课本图29．2-8中的几何体可以看成什么样的几何体被挖去一部分什么样的几何体而成的？三视图中为什么出现虚线？ 二、自学检测：1.在右图中（1）是几何体(2) 的______视图.2.下图中几何体的两种视图正确的一组是（ ）3.“圆柱与球的组合体”如图所示，则它的三视图是（ ）三、交流反馈：四、当堂训练1．小琳过14周岁生日，父母为她预定的生日蛋糕如图所示，它的主视图应该是（ ）2.如图所示的正四棱锥的俯视图是( )3．下面左图所示的几何体的俯视图是（ ）蛋糕 A B C DA. B. C. D. 4．如图所示几何体的左视图是（ ）A. B. C. D5．如图，添线补全下列三个几何体对应的三视图．6．分别画出下列各物体的三视图．五、拓展应用1.如图是一个圆柱截去四分之一后得到的几何体，以如图所示的一个截面为正面，请画出它的三种视图．正面。

三视图导学学案学习目标：知识与技能：1、理解三投影面体系2、理解三视图的形成（正投影法）以及展开2、理解三视图反映物体的方位关系4、理解并掌握三视图的投影规律5、学会绘制简单的三视图过程与方法：经历三视图的形成以及绘制过程，体验从设计构思转化为设计语言的过程情感、态度和价值观领略三视图绘制的重要性，体验技术语言的魅力重点：三视图的形成原理和规律；学习并掌握三视图的画法。

难点：三视图的识读与绘制并能根据不完整的三视图猜测还原出物体学习过程：（一）理解投影原理Ⅰ、知道什么是正投影，思考：什么样的投影最能准确表达物体的形状和大小？Ⅱ、视图：物体向投影面投影所得到的图形，称为视图。

如以下图所示的三个几何体，沿箭头方向的竖直面上正投影得到的视图分别是什么形状？Ⅲ、思考：如何用视图准备表达右图所示几何体的形体特征呢？三视图的原理和识图1、三投影体系：2、三视图的形成：在绘制技术图样时，将物体在三个相互垂直的平面内作垂直投影所得的三个图形，称为三视图。

主视图：由向投影，在正面V上得到的视图。

俯视图：由向投影，在水平面H上得到的视图。

左视图：由向投影，在侧面W上得到的视图。

请同学们在投影面上画出三棱椎在三个投影面上的视图，然后将三个投影面展开，分析：3、三视图的展开：每一个视图分别反映实物长、宽、高中的哪两个尺寸？主视图反映了物体的和；府视图反映了物体的和；左视图反映了物体的和；注意：左视图的宽是水平尺寸，而府视图的宽是竖直尺寸4、三个视图之间的关系：（1）位置关系：主视图不动，左视图在主视图的边，俯视图在主视图的边。

（2）投影关系：主视图和俯视图：长；主视图和左视图：高；俯视图和左视图：宽；(3)方位关系：三个视图的上、下、左、右与实物的上、下、左、右、前、后的对应关系是：主视图的上、下、左、右的、、、；俯视图的上、下、左、右的、、、；左视图的上、下、左、右的、、、；预习教材P75—P76，完成下列练习：7、根据三视图还原物体的实物图8、下列三视图中俯视图不完整，请补画出来（提示：先猜想出物体的实物图）俯视图左视图 主视图 主视图 俯视图 左视图。

三视图导学案一、学习要求本期我们主要学习几何体的三视图，要求会画圆柱、圆锥、球、直三棱柱、直四棱柱等简单几何体的三视图，理解三视图的相对性．通过三视图进一步掌握常见几何体的性质．二、知识梳理1．视图：从上面、正面和侧面（左边或右边）三个不同的方向看一个物体，然后描绘出所看到的三张图，就是视图．注意：通过视图我们可以将一个立体图形转换成平面的图形．2．三视图：如果一个物体的主视图、俯视图和左视图保持“长对正、高平齐、宽相等”，通常把它们合称为这个物体的三视图．三视图包括主视图、俯视图和左视图．主视图：从正面看到的视图；俯视图：从上面看到的图形；左视图：从左边看到的视图．注意：主视图、俯视图和左视图都是相对于观察者而言的，位于物体不同方向的观察者，他们所画出的三视图可能是不一样的．三、解题指导1．常见几何体的视图我们习题中所要画的物体的视图，大多由这些物体简单组合而成．2．视图与投影三视图实际上也是一种投影，叫做正投影，当投射光线与投影面垂直时，所形成的投影就是视图．如图，图中的正投影就是圆柱的主视图3．画三视图的注意事项首先确定三视图的位置，画出主视图，然后在主视图的下面画出俯视图，在主视图的右边画出左视图．主视图只要反映的是物体的长和高，俯视图只要反映物体的长和宽，左视图主要反映物体的高和宽，因此画三视图时，主、俯视图要长对正，主、左视图要高平齐，左、俯视图要宽相等．另外，画对称物体的视图时，要先画物体的对称轴或中心线，用点画线表示（画好后可擦去）．在画视图时，看得见部分的轮廓线通常画成实线，看不见的部分的轮廓线通常画成虚线．4．在画三视图时，如果实在想不出三视图的形状，可以简单地实验辅助思考．四、数学思想方法1．空间想象能力对于简单物体的三视图，我们要能识别观察方向，能够想像出物体的原型，这就需要我们具备一定的空间想象能力．2．抽象思维能力在解视图与投影有关的问题的时候，我们经常需要把实际问题抽象成平面几何中的有关三角形的问题，从而解决实际问题的能力得到发展．。

29.2 三视图第1课时三视图【学习目标】〔一〕知识技能：1.会从投影角度理解视图的概念。

2.会画几何体的三视图。

〔二〕数学思考：通过具体活动，积累观察，想象物体投影的经验。

〔三〕解决问题：会画实际生活中简单物体的三视图。

〔四〕情感态度：1.培养学生自主学习与合作学习相结合的学习方式，使学生体会从生活中发现数学。

2.在应用数学解决生活中问题的过程中，品尝成功的喜悦，激发学生应用数学的热情。

【学习重点】1.从投影的角度加深对三视图概念的理解。

2.会画简单几何体的三视图。

【学习难点】1.对三视图概念理解的升华。

2.正确画出三棱柱的三视图和小零件的三视图。

【学习过程】【情境引入】活动一如图，直三棱柱的侧棱与水平投影面垂直。

请与同伴一起探讨下面的问题：（1）以水平投影面为投影面，在正投影下，这个直棱柱的三条侧棱的投影是什么图形？（2）画出直三棱柱在水平投影面的正投影，得到的投影是什么图形？它与直三棱柱的底面有什么关系？〔3〕这个水平投影能完全反映这个物体的形状和大小吗？如不能，那么还需哪些投影面？【自主探究】活动二学生观察思考：〔1〕三个视图位置上的关系。

〔2〕三个视图除了位置上的关系，在大小尺寸上，彼此之间又存在什么关系？小结：1.三视图位置有规定，主视图要在，俯视图应在，左视图要在。

2.三视图中各视图的大小也有关系。

主视图与俯视图表示同一物体的，主视图与左视图表示同一物体的，左视图与俯视图表示同一物体的。

因此三视图的大小是互相联系的。

画三视图时，三个视图要放在正确的位置，并且使主视图与俯视图的，主视图与左视图的，左视图与俯视图的。

活动三例1 画出以以下图2所示的一些根本几何体的三视图.题后小结:画这些根本几何体的三视图时，要注意从个方面观察它们.具体画法为: 视图的位置，画出视图;视图正下方画出视图，注意与主视图“〞。

视图正右方画出视图.注意与主视图“〞，与俯视图“〞. 【稳固练习】1.画出图中的几何体的三视图。

精选教课教课设计设计 | Excellent teaching plan
教师学科教课设计
[ 20–20学年度第__学期]
任教课科： _____________
任教年级： _____________
任教老师： _____________
xx市实验学校
育人好像春风化雨，授业不惜蜡炬成灰
精选教课教课设计设计| Excellent teaching plan
三视图（ 2）导教案
学习目标：
1、掌握由三视图想几何体的形状的方法。

2、掌握由三视图画几何体。

独立自学：
1、阅读教材p112至113面内容，说出由三视图想像几何体的方
法，掌握由三视图画几何体，模拟例题画几何体。

2、完成第114面练习。

3、完成教案第171面习题。

合作互学：
1、小组互查学习内容掌握状况。

2、交流习题的解法。

展现竟学：
各小组代表展现学习成就，发布自己的见解。

精讲导学：
归纳重难点、针对学生学习中出现的问题讲解和重申。

检测故学：
教案第 172 面习题。

育人好像春风化雨，授业不惜蜡炬成灰。

例2 观察三视图，想象并说出它的几何结构特征，然后画出该几何体的示意图：
练习
3．根据下列三视图，想象对应的几何体：
（1）（2）
三．学习心得
1.你认为画空间几何体的三视图应该注意那些问题？
2.由三视图怎样想象空间几何体？
四．课堂检测
1．关于三视图有以下几种说法：
①任何物体的三视图都与物体的摆放位置有关；
②任何物体的三视图都与物体的摆放位置无关；
③有些物体的三视图与物体的摆放位置无关．
其中正确的说法是______．(只填序号)
2.如图，在正方体ABCD-A1B1C1D1中，M、N分别是BB1、BC的中点，则图中阴影部分在平面ADD1A1上的投影为()
3.四个正方体按如图所示的方式放置，其中阴影部分为我们观察的正面．则该物体的三视图正确的为( )
4．若某空间几何体的三视图如右图所示，则该几何体为()
A．三棱柱B．三棱锥
C．四棱柱D．四棱锥
5．(2010年高考北京卷)一个长方体去掉一个小长方体，
所得几何体的正视图与侧视图分别如图所示，则该几何体的俯视图为()
学习数学的大道上荆棘丛生，这也是好事，常人望而却步，只有意志坚强的人例外-----雨果。

正投影与三视图导学案
（1）三视图间的位置关系
俯视图在主视图的方，左视图在主视图的方。

（2）形体与视图的方位关系
任何形体在空间都具有上、下、左、右、前、后六个方位，形体在空间的六个方位和三视图所反映形体的方位
主视图——反映了形体的方位关系；
俯视图——反映了形体的方位关系；
左视图——反映了形体的方位关系。

（3）每个视图所反映的形体尺寸情况
主视图——反映了形体尺寸。

俯视图——反映了形体尺寸。

左视图——反映了形体尺寸。

根据每个视图所反映的形体的尺寸情况及投影关系，有：（九字口诀）1．绘制三视图：参照轴测图，根据给定的两投影面，画出第三投影（左视图）。

主视方向2．画出下图的三视图
主视方向
牛刀小试：
1.如图，空心圆柱的左视图是（）。

第三节设计的表达与交流
——三视图导学案
学习目标：1、掌握三投影体系的组成；2、理解三视图形成的原理；
3、掌握三视图之间的投影规律；
4、通过练习提高识图能力。

探究任务：投影对应关系（要求：在黑板上标注相应的关系）1、物体有长、宽、高三个方向的尺寸。

通常规定：物体左右之间的距离为长（x）；前后之间的距离为宽（Y）；上下之间的距离为高（Z）；由下图可知：一个视图只能反映物体两个方向的尺寸。

主视图反映物体的左右即（X）和物体上下即（Z）。

俯视图反映物体的左右即（X）和物体前后即（Y）。

左视图反映物体的上下即（Z）和物体前后即（Y）。

通过以上分析，三视图
之间的投影关系可以概括
为：
主、俯视图
主、左视图
左、俯视图
2、三视图之间的方位关系
物体有上、下、左、右、前、后六个方位，由下图可知：
主视图反映物体的、
和、的相对位置关系；
俯视图反映物体的、
和、的相对位置关系；
左视图反映物体的、
和、的相对位置关系。

能力提升：(补线，共五个模型)
要求：1、选择手中模型对应的三视图，先说明各个视图的名称，然后进行补线。

可见的轮廓线用实线，不可见的轮廓线用虚线；
2、补对一条线得1分，正确说明你补该线的理由得1分，补错一条线不得分。

模型1
模型4
模型2
模型3
模型5。

29.2三视图（2）学习目标：1、学会根据物体的三视图描述出几何体的基本形状或实物原型．2、经历探索简单的几何体的三视图的还原过程，进一步发展空间想象能力．3、了解将三视图转换成立体图在生活中的作用，使学生体会到所学的知识有重要的实用价值．学习重点：根据三视图描述基本几何体和实物原型及三视图在生活中的作用．学习难点：根据物体的三视图描述出几何体的基本形状或实物原型．学习过程：一、新知引入根据如图右边的椅子的视图,工人就能制造出符合设计要求的椅子.（展示图片）二、新知讲解探究点一：会根据物体的三视图还原出物体活动1根据下面的三视图说出立体图形的名称．分析：由三视图想象立体图形时，要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面，然后再综合起来考虑整体图形．活动2 根据物体的三视图(如图)描述物体的形状．讨论：怎样由物体的三视图想象出原物体的形状？●归纳：由三视图想象立体图形时，先分别根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状，然后再综合起来考虑整体图形．例题讲解:例、根据物体的三视图(如图)，描述物体的形状.注意：根据左视图、俯视图、主视图想象出它在空间里的形状，从而确定物体的物状．巩固练习：1．如下图为一个几何体的三视图，那么这个几何体是___________．2.下面所给的三视图表示什么几何体?3．根据下列物体的三视图，填出几何体的名称：（1）如图1所示的几何体是____________；（2）如图2所示的几何体是____________.4.若某几何体的三视图如图所示，则这个几何体是（）5.如图所示，是一些完全相同的小正方体搭成的几何体的三视图.这个几何体只能是（）探究点二：由三视图确定组合体的数据例、一个几何体由大小相同的小立方块搭成，从上面看到的几何体的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到几何体的形状是图中的( )巩固练习：1.如图是由棱长为的正方体搭成的某几何体三视图，则图中棱长为的正方体的个数是( )A．5 B．8 C．7 D．62.学校小卖部货架上摆放着某品牌方便面，它们的三视图如图，则货架上的方便面至少有（）A．7 B．8 C．9 D．103.由若干个小正方体搭成的几何体的主视图和俯视图，如图所示，则搭成该几何体所用的小正方体的个数最少是（）A.8 B．9 C．10 D．11活动3某工厂要加工一批密封罐，设计者给出了密封罐的三视图(如下图)，请你按照三视图确定制作每个密封罐所需钢板的面积．分析：对于某些立体图形，若沿其中一些线(例如棱柱的棱)剪开，可以把立体图形的表面展开成一个平面图形，即展开图．在实际的生产中，三视图和展开图往往结合在一起使用．解决本题的思路是，由视图想象出密封罐的立体形状，再进一步画出展开图，从而计算面积．巩固练习：1.长方体的主视图和左视图如下图所示（单位：cm），则其俯视图的面积是_________cm2.2.由若干个边长为1 cm的正方体堆积成一个几何体，它的三视图如图所示，则这个几何体的表面积是（）A. 15 cm2B. 18 cm2C. 21 cm2D. 24 cm23. 如图是某几何体的三视图，根据图中数据，可得该几何体的体积为（）A. 60πB. 70πC. 90πD. 160π4.如图是一个几何体的三视图(单位：厘米)．(1)写出这个几何体的名称；(2)根据所示数据计算这个几何体的表面积；(3)如果一只蚂蚁要从这个几何体中的点B出发，沿表面爬到AC的中点D，请你求出这个线路的最短路程解：三、课堂小结1．一个视图不能确定物体的空间形状，根据三视图要描述几何体或实物原型时，必须将各视图对照起来看．2．一个摆好的几何体的视图是唯一的，但从视图反过来考虑几何体时，它有多种可能性．例如：正方体的主视图是正方形，但主视图是正方形的几何体有直三棱柱、长方体、圆柱等．3．对于较复杂的物体，由三视图想象出物体的原型，应理解并掌握三个视图之间的前后、左右、上下的对应关系．四、布置作业101页练习1、2题当堂测评1、如图是由几个相同的小正方体搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（）A. 个B. 个C. 个D. 个2、如图是三个大小不等的正方体拼成的几何体，其中两个较小正方体的棱长之和等于大正方体的棱长．该几何体的主视图、俯视图和左视图的面积分别是，，，则，，的大小关系是（）A. B. C. D.3、如图是某几何体的三视图及相关数据，则判断正确的是（）A. B.C. D.4、如图①是一个几何体的主视图和左视图．某班同学在探究它的俯视图时，画出了如图②的几个图形，其中，可能是该几何体俯视图的共有（）A. 个B. 个C. 个D. 个5、由个相同的小正方体堆成的几何体，其视图如图所示，则的最大值是 .6、如图是某几何体从正面、左面和上面看到的平面图形，根据图中数据，求得该几何体的体积为__________．7、如图，是由一些小立方块所搭几何体的三种视图，若在所搭几何体的基础上（不改变原几何体中小立方块的位置），继续添加相同的小立方块，以搭成一个大正方体，至少还需要个小立方块．8、用小立方块搭成一个几何体，从正面看和从上面看所得的平面图形如图所示，搭建这样的几何体最多要几个小立方块？最少要几个小立方块？9、如图，水平放置的长方体的底面是边长为和的矩形，它的左视图的面积为，则长方体的体积是多少？。

29.2三视图导学案班级：姓名：自评等级：一、自主学习1.画三视图时，首先确定主视图的位置.画出主视图，然后在主视图的下面画出俯视图，在主视图的右面画出左视图.主视图反映物体的_______和_______，俯视图反映物体的_______和_______，左视图反映物体的_______和_______.因此，画三视图时，主、俯视图要长对正，主、左视图要高平齐，左、俯视图要宽相等.看得见部分的轮廓线通常画成实线，看不见部分的轮廓线通常画成虚线.2.在下列几何体中，主视图是圆的是( )3.如图所示的水杯的俯视图是( )二、基础巩固4.如图所示，空心圆柱体在指定方向上的视图正确的是( )5.小明从正面观察图所示的两个物体，看到的是图中的( )6.某同学把图所示的几何体的三种视图画出如图①②③所示(不考虑尺寸)；其中错误的是哪个图?答：7.一个几何体的三种视图如图所示，则这个几何体是( )A.圆柱B.圆锥C.长方体D.正方体8.一个物体的正视图、俯视图如图所示，请你画出该物体的左视图并说出该物体形状的名称.：三、能力提高9.桌上摆着一个由若干个相同正方体组成的几何体，其主视图和左视图如图所示，这个几何体最多可以由___________个这样的正方体组成.10.将图所示的阴影部分剪下来，围成一个几何体的侧面，使AB、DC重合，则所围成的几何体图形是( )11.如图所示，说出下列四个图形各是由哪些立体图形展开得到的?四、模拟链接12.由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图所示.(1)请你画出这个几何体的一种左视图.(2)若组成这个几何体的小正方体的块数为n，请你写出n的所有可能值.。

九年级数学《三视图（2）》导学案【学习目标】1、进一步明确正投影与三视图的关系。

2、经历探索三棱柱和四棱柱的三视图的画法，能识别棱柱的三视图。

3、掌握在画三视图时何时画成实线，何时画成虚线。

【学习重难】重点：三棱柱和四棱柱的三视图的画法，能识别棱柱的三视图。

难点：掌握在画三视图时何时画成实线，何时画成虚线。

【学习准备】正方体、小长方体、圆柱、圆锥、球体、棱柱等实物模型组合。

【导学流程】（一）感知情境，温故知新。

1、画一个立体图形的三视图时要注意什么？（小组交流展示、总结）2、说一说：直三棱柱、圆柱、圆锥、球的三视图。

（组内相互说、画）（二）自主探究，学习新知。

活动1：阅读教材P96页的例1，完成下列各题：1、圆柱对应的主视图是（）。

A B C D2、主视图、左视图、俯视图都是圆的几何体是（）。

A、圆锥B、圆柱C、球D、空心圆柱3、画出下列几何体的三视图活动2：阅读教材P97页的例2，观察、理解、归纳：1、画组合图形的三视图时，__________的部分的轮廓线画成实线，_________的部分的轮廓线画成虚线。

2、组合体的各部分的视图也要注意三视图的位置摆放和大小关系。

即“长，高，宽。

”（三）合作学习，小组评比。

活动3：画出下图所示的一些组合体的三视图。

（加分奖励）先小组成员独立画图，然后小组内互评，选一名同学展示，其他组纠错。

活动4：小组合作，交流再展示：画出下列几何体的三视图。

（四）达标互评，展示交流。

1．沿圆柱体上底面直径截去一部分后的物体如图所示，它的俯视图是（）2．如图所示，画出该物体的三视图。

3．一个透明的玻璃正方体内镶嵌了一条铁丝(如图所示的粗线)，请画出该正方体的三视图。

4．分别画出下面组合体的三视图.5．分别画出图中由7个小正方体组合而成的几何体的三视图。

（五）小组评价，反思收获。

1、你学会了什么？2、你存在的问题？（六）拓展迁移，作业设计。

1．完成教材P102-103页习题29.2第6-7题。

数学：29.2《三视图》导学案2（人教版九年级下）课 题 29.2 课 型 新授课执笔人审核人级部审核学习时间 第15周第 4导学稿教师寄语今日事，今日毕。

不要把今天的事拖到明天。

学习目标 1、学会根据物体的三视图描述出几何体的基本形状或实物原型；2、经历探索简单的几何体的三视图的还原，进一步发展空间想象能力。

3、由三视图进行简单几何体的有关计算学习重点 根据物体的三视图描述出几何体的基本形状或实物原型 学习难点学生空间想象能力的培养．学生自主活动材料一、前置自学1、球体的三种视图是（ ）A.三个圆B.两个圆和一个长方形C.两个圆和一个半圆D.一个圆和两个半圆 2、如右图是某几何体的三种视图，则该几何体是（ ）A.正方体B.圆锥体C.圆柱体D.球体 3、如果一个立体图形的主视图为矩形，则这个立体图形可能是 。

二、合作探究一个几何体的三视图如图所示，它的俯视图为菱形．请写出该几何体的形状，并根据图中所给的数据求出它的侧面积。

三、拓展提升1、圆柱的左视图是 ，俯视图是 . 、2、如果一个几何体的主视图、左视图与俯视图都是一样的图形，那么这个几何体可能是＿＿.3、一个圆柱的轴截面平行于投影面,圆柱的正投影是一个边长为10的正方形,求圆柱的体积主视图俯视图左视图4cm 3cm8cm俯视图主（正）视图左视图和表面积.四、当堂反馈1、一个物体的三视图如右图所示，该物体是（ ）A. 圆柱B. 圆锥C. 棱锥D. 棱柱 2、如图，上下底面为全等的正六边形礼盒，其正视图与左视图均由矩形构成，正视图中大矩形边长如图所示，侧视图中包含两全等的矩形，如果用彩色胶带如图包扎礼盒，所需胶带长度至少为（ ）A ．320c mB ．395.24 cmC ．431.76 cmD ．480 cm3、如图是由一些完全相同的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用的小立方块的个数是（ ）A .5个 B. 6个 C. 7个 D. 8个4、一个几何体的三视图如图所（其中标注的a b c ，，为相应的边长），则这个几何体的体积是 ．acbcba5、长方体的主视图与左视图如图所示，则其俯视图的面积是多少？实物图正视图左视图20cm20cm60cm左视图主视图俯视图左视图主视图2342。