人教九年级下册数学- 由三视图确定几何体的面积或体积导学案
- 格式:doc
- 大小:1010.02 KB
- 文档页数:5



29.2 三视图第3课时由三视图确定几何体的面积或体积1.能根据三视图求几何体的侧面积、表面积和体积等;(重点)2.解决实际生活中与面积、体积等方面有关的实际问题.(难点)一、情境导入已知某混凝土管道的三视图,你能根据三视图确定浇灌每段这种管道所需混凝土的体积吗(π=3.14)?二、合作探究探究点:由三视图确定几何体的面积或体积【类型一】由三视图求几何体的侧面积已知如图为一几何体的三视图:(1)写出这个几何体的名称;(2)若从正面看的长为10cm,从上面看的圆的直径为4cm,求这个几何体的侧面积(结果保留π).解析:(1)根据该几何体的主视图与左视图是矩形,俯视图是圆可以确定该几何体是圆柱;(2)根据告诉的几何体的尺寸确定该几何体的侧面积即可.解:(1)该几何体是圆柱;(2)∵从正面看的长为10cm,从上面看的圆的直径为4cm,∴该圆柱的底面直径为4cm,高为10cm,∴该几何体的侧面积为2πrh=2π×2×10=40π(cm2).方法总结:解题时要明确侧面积的计算方法,即圆柱侧面积=底面周长×圆柱高.变式训练:见《学练优》本课时练习“课堂达标训练”第3题【类型二】由三视图求几何体的表面积如图是两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个几何体的表面积.解析:先由三视图得到两个长方体的长,宽,高,再分别表示出每个长方体的表面积,最后减去上面的长方体与下面的长方体的接触面面积即可.解:根据三视图可得:上面的长方体长6mm,高6mm,宽3mm,下面的长方体长10mm,宽8mm,高3mm,这个几何体的表面积为2×(3×8+3×10+8×10)+2×(3×6+6×6)=268+108=376(mm2).答:这个几何体的表面积是376mm2.方法总结:由三视图求几何体的表面积,首先要根据三视图分析几何体的形状,然后根据三视图的投影规律—“长对正,高平齐,宽相等”,确定几何体的长、宽、高等相关数据值,再根据相关公式计算几何体的面积.注意:求解组合体的表面积时重叠部分不应计算在内.变式训练:见《学练优》本课时练习“课堂达标训练” 第4题【类型三】 由三视图求几何体的体积某一空间图形的三视图如图所示,其中主视图是半径为1的半圆以及高为1的矩形;左视图是半径为1的四分之一圆以及高为1的矩形;俯视图是半径为1的圆,求此图形的体积(参考公式:V 球=43πR 3).解析:由已知中的三视图,我们可以判断出该几何体的形状为下部是底面半径为1,高为1的圆柱,上部是半径为1的14球组成的组成体,代入圆柱体积公式和球的体积公式,即可得到答案.解:由已知可得该几何体是一个下部为圆柱,上部为14球的组合体.由三视图可得,下部圆柱的底面半径为1,高为1,则V 圆柱=π,上部14球的半径为1,则V 14球=13π,故此几何体的体积为错误!.方法总结:由三视图求几何体的体积,首先要根据三视图分析几何体的形状,然后根据三视图的投影规律“长对正,高平齐,宽相等”确定几何体的长、宽、高等相关数据值.再根据相关公式计算几何体各部分的体积并求和.变式训练:见《学练优》本课时练习“课堂达标训练”第6题【类型四】 由三视图确定几何体面积或体积的实际应用杭州某零件厂刚接到要铸造5000件铁质工件的订单,下面给出了这种工件的三视图.已知铸造这批工件的原料是生铁,待工件铸成后还要在表面涂一层防锈漆,那么完成这批工件需要原料生铁多少吨?涂完这批工件要消耗多少千克防锈漆(铁的密度为7.8g/cm 3,1kg 防锈漆可以涂4m 2的铁器面,三视图单位为cm)?解析:从主视图和左视图可以看出这个几何体是由前后两部分组成的,呈一个T 字形状.故可以把该几何体看成两个长方体来计算.解:∵工件的体积为(30×10+10×10)×20=8000cm 3,∴重量为8000×7.8=62400(g)=62.4(kg),∴铸造5000件工件需生铁5000×62.4=312000(kg)=312(t).∵一件工件的表面积为2×(30×20+20×20+10×30+10×10)=2800cm 2=0.28m 2.∴涂完全部工件需防锈漆5000×0.28÷4=350(kg).方法总结:本题主要考查了由三视图确定几何体和求几何体的面积;关键是得到几何体的形状,得到所求的等量关系的相对应的值.变式训练:见《学练优》本课时练习“课后巩固提升”第7题三、板书设计1.由三视图求几何体的侧面积;2.由三视图求几何体的表面积;3.由三视图求几何体的体积.本节重在引导学生总结解决此类问题的方法和规律,探究其实质.在小组讨论的过程中,学生了解了三视图中相关数据的对应关系,即“长对正,高平齐,宽相等”,找到了解决问题的根本,通过具体的例题,让学生进行练习,巩固学习效果.。

29.2 三视图第2课时由三视图确定几何体1.会根据俯视图画出一个几何体的主视图和左视图; (重点) 2.体会立体图形的平面视图效果,并会根据三视图还原立体图形.(难点)一、情境导入让学生拿出准备好的六个小正方体,搭一个几何体,然后让学生画出几何体的俯视图,并选择一位学生上台演示并在黑板上画出俯视图(如右图),教师在正方体上标上数字并说明数字含义.问:能不能根据上面的俯视图画出这个几何体的主视图和左视图?看哪些同学速度快.二、合作探究探究点:由三视图确定几何体【类型一】根据三视图判断简单的几何体一个几何体的三视图如图所示,则这个几何体是( )A.四棱锥 B.四棱柱C.三棱锥 D.三棱柱解析:主视图是由两个矩形组成,而左视图是一个矩形,俯视图是一个三角形,得出该几何体是一个三棱柱.故选D.方法总结:由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.变式训练:见《学练优》本课时练习“课堂达标训练”第1题【类型二】由三视图判断实物图的形状下列三视图所对应的实物图是( )解析:从俯视图可以看出实物图的下面部分为长方体,上面部分为圆柱,圆柱与下面的长方体的顶面的两边相切且与长方体高度相同.只有C满足这两点,故选C.方法总结:主视图、左视图和俯视图是分别从物体正面、左面和上面看所得到的图形.对于本题要注意圆柱的高与长方体的高的大小关系.变式训练:见《学练优》本课时练习“课堂达标训练”第3题【类型三】根据俯视图中小正方形的个数判断三视图如图,是由几个小立方体搭成的几何体的俯视图,小正方形中的数字表示在该位置上的立方体的个数,这个几何体的主视图是( )解析:由俯视图可知,几个小立方体所搭成的几何体如图所示:,可知选项D为此几何体的主视图.方法总结:由俯视图想象出几何体的形状,然后按照三视图的要求,得出该几何体的主视图和侧视图.变式训练:见《学练优》本课时练习“课堂达标训练”第4题【类型四】由主视图和俯视图判断组成小正方体的个数如图,是由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数是( )A.5个或6个 B.6个或7个C.7个或8个 D.8个或9个解析:从俯视图可得最底层有4个小正方体,由主视图可得上面一层是2个或3小正方体,则组成这个几何体的小正方体的个数是6个或7个.故选B.方法总结:运用观察法确定该几何体有几列以及每列小正方体的个数是解题关键.变式训练:见《学练优》本课时练习“课堂达标训练”第2题【类型五】由三视图判断组成物体小正方体的个数由若干个相同的小立方体搭成的几何体的三视图如图所示,则组成该几何体的小立方体有( )A.3块 B.4块 C.5块 D.6块解析:由俯视图易得最底层有3个立方体,第二层有1个立方体,那么组成该几何体的小立方体有3+1=4(个).故选B.方法总结:解决此类问题时要借助三种视图表示物体的特点,从主视图上弄清物体的上下和左右形状;从俯视图上弄清物体的左右和前后形状;从左视图上弄清物体的上下和前后形状.综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意.变式训练:见《学练优》本课时练习“课后巩固提升”第3题【类型六】由三视图确定几何体的探究性问题(1)请你画出符合如图所示的几何体的两种左视图;(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.解析:(1)由俯视图可得该几何体有2行,则左视图应有2列.由主视图可得共有3层,那么其中一列必有3个正方体,另一列最少是1个,最多是3个;(2)由俯视图可得该组合几何体有3列,2行,以及最底层正方体的个数及摆放形状,由主视图结合俯视图可得从左边数第2列第2层最少有1个正方体,最多有2个正方体,第3列第2层最少有1个正方体,最多有2个正方体,第3层最少有1个正方体,最多有2个正方体,分别相加得到组成组合几何体的最少个数及最多个数即可得到n的可能值.解:(1)如图所示:(2)∵俯视图有5个正方形,∴最底层有5个正方体.由主视图可得第2层最少有2个正方体,第3层最少有1个正方体;或第2层最多有4个正方体,第3层最多有2个正方体,∴该组合几何体最少有5+2+1=8个正方体,最多有5+4+2=11个正方体,∴n可能为8或9或10或11.方法总结:解决本题要明确俯视图中正方形的个数是几何体最底层正方体的个数.变式训练:见《学练优》本课时练习“课后巩固提升”第8题三、板书设计1.由三视图判断几何体的形状;2.由三视图判断几何体的组成.本课时的设计虽然涉及知识丰富,但忽略了学生的接受能力,教学过程中需要老师加以引导.通过很多老师的点评,给出了很多很好的解决问题的办法,在以后的教学中,要不断完善自己,使自己的教学水平有进一步的提高.。



29.2 三视图第3课时由三视图确定几何体的面积或体积【学习目标】1、学会根据物体的三视图描述出几何体的基本形状或实物原型。
2、经历探索简单的几何体的三视图的还原,进一步发展空间想象能力进而求面积或体积。
3、了解将三视图转换成立体图形在生产中的作用,使学生体会到所学知识有重要的实用价值。
【学习重点】根据三视图描述基本几何体和实物原型及三视图在生产中的作用。
【学习难点】根据三视图想象基本几何体实物原型求面积或体积。
【学习过程】【问题情境】让学生欣赏事先准备好的机械制图中三视图与对应的立体图片,借助图片信息,让学生体会本章知识的价值。
并借此可以讲述一下现在一些中专、中技甚至大学开设的模具和机械制图专业的课程都需要这方面的知识,激发学生学习兴趣,导入本课。
【自主探究】根据下列几何体三视图,画出它们的表面展开图:(1解:(1)该物体是:(2)该物体是:画出它的展开图是:画出它的展开图是:【合作探究】例6某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积。
问题:要想救出每个密封罐所需钢板的面积,应先解决哪些问题? 小组讨论结论:1、应先由三视图想象出物体的 ; 2、画出物体的 ;解:该物体是:画出它的展开图是:它的表面积是:变式训练:如图,上下底面为全等的正六边形的礼盒,其主视图与左视图均由矩形构成,主视图中大矩形的边长如图所示,左视图中包含两个全等的矩形。
如果用彩色胶带如图包扎礼盒,所需胶带长度至少为( )A 、120cmB 、395.24cmC 、431.76cmD 、480cm【归纳总结】物体的形状、物体的三视图、物体的展开图三者相互联系、相互转化,我们可以由三构造几何原型,进而画出它的展开图,还可求表面积和体积等。
【合作探究】如图,一个空间几何体的主视图和左视图都是边长为1的三角形,俯视图是一个圆,那么这个几何体的侧面积是( ) A 、41π B 、42π C 、22π D 、21π变式训练:如图是一个几何体的三视图:(1)写出这个几何体的名称;(2)根据所示数据计算这个几何体的表面积;(3)如果一只蚂蚁要从这个几何体中点B出发,沿表面爬行到AC的中点D,请求出这个路线的最短路程。


初中数学人教版九年级下册同步教学设计29-2 第2课时《由三视图确定几何体》一. 教材分析人教版初中数学九年级下册第29-2节《由三视图确定几何体》的内容,是在学生已经掌握了立体图形的性质、展开图与立体图形的对应关系等知识的基础上进行的一节实践性较强的课程。
本节课通过让学生观察、分析、推理三视图与几何体的关系,提高学生的空间想象能力,培养学生的逻辑思维能力。
教材内容主要包括:三视图的概念及其作用、几何体的三视图特征、由三视图确定几何体等。
二. 学情分析九年级的学生在经历了多年的数学学习后,已经具备了一定的空间想象能力和逻辑思维能力。
但是,对于如何准确、快速地由三视图确定几何体,部分学生可能还存在一定的困难。
因此,在教学过程中,教师需要关注这部分学生的学习需求,通过合理的教学设计,帮助他们提高空间想象能力和逻辑思维能力。
三. 教学目标1.让学生掌握三视图的概念及其作用,了解几何体的三视图特征。
2.培养学生观察、分析、推理的能力,提高空间想象能力。
3.使学生能够运用所学知识解决实际问题,培养学生的应用能力。
四. 教学重难点1.重点:三视图的概念及其作用,几何体的三视图特征。
2.难点:如何准确、快速地由三视图确定几何体。
五. 教学方法1.情境教学法:通过生活实例引入课题,激发学生的学习兴趣。
2.合作学习法:引导学生分组讨论,培养学生的团队协作能力。
3.实践操作法:让学生动手操作,提高学生的实践能力。
4.引导发现法:教师引导学生发现规律,培养学生的推理能力。
六. 教学准备1.教具:立体模型、投影仪、幻灯片等。
2.学具:学生用书、练习册、文具等。
七. 教学过程1.导入(5分钟)教师通过展示一些生活中的几何体,如建筑、家具等,引导学生观察这些几何体的形状,让学生体会几何体在现实生活中的应用。
然后,提问:“如果只给你一个几何体的主视图、俯视图和左视图,你能确定这个几何体吗?”从而引出本节课的课题。
2.呈现(10分钟)教师通过幻灯片展示几何体的三视图,让学生了解三视图的概念及其作用。

全新修订版教学设计
(学案)
九年级数学下册
老师的必备资料
家长的帮教助手
学生的课堂再现
人教版(RJ)
29.2 三视图
第3课时由三视图确定几何体的面积或体积
【学习目标】
1、学会根据物体的三视图描述出几何体的基本形状或实物原型。
2、经历探索简单的几何体的三视图的还原,进一步发展空间想象能力进而求面积或体积。
3、了解将三视图转换成立体图形在生产中的作用,使学生体会到所学知识有重要的实用价
值。
【学习重点】根据三视图描述基本几何体和实物原型及三视图在生产中的作用。
【学习难点】根据三视图想象基本几何体实物原型求面积或体积。
【学习过程】
【问题情境】让学生欣赏事先准备好的机械制图中三视图与对应的立体图片,借助图片信息,让学生体会本章知识的价值。
并借此可以讲述一下现在一些中专、中技甚至大学开设的模具和机械制图专业的课程都需要这方面的知识,激发学生学习兴趣,导入本课。
【自主探究】根据下列几何体三视图,画出它们的表面展开图:
(1。
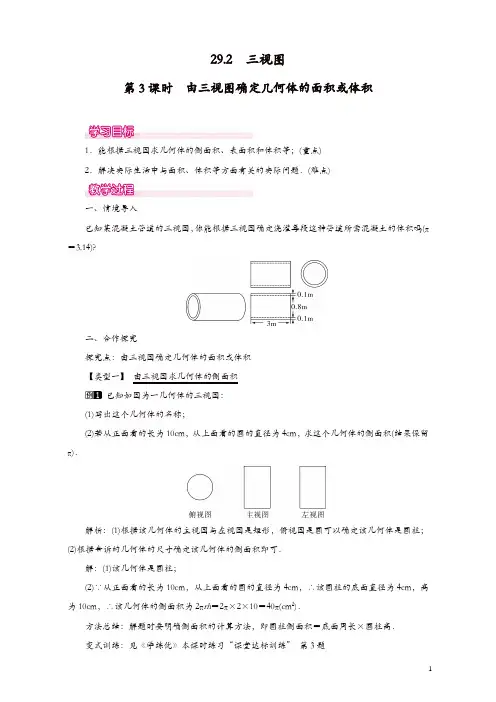
29.2 三视图第3课时由三视图确定几何体的面积或体积1.能根据三视图求几何体的侧面积、表面积和体积等;(重点)2.解决实际生活中与面积、体积等方面有关的实际问题.(难点)一、情境导入已知某混凝土管道的三视图,你能根据三视图确定浇灌每段这种管道所需混凝土的体积吗(π=3.14)?二、合作探究探究点:由三视图确定几何体的面积或体积【类型一】由三视图求几何体的侧面积已知如图为一几何体的三视图:(1)写出这个几何体的名称;(2)若从正面看的长为10cm,从上面看的圆的直径为4cm,求这个几何体的侧面积(结果保留π).解析:(1)根据该几何体的主视图与左视图是矩形,俯视图是圆可以确定该几何体是圆柱;(2)根据告诉的几何体的尺寸确定该几何体的侧面积即可.解:(1)该几何体是圆柱;(2)∵从正面看的长为10cm,从上面看的圆的直径为4cm,∴该圆柱的底面直径为4cm,高为10cm,∴该几何体的侧面积为2πrh=2π×2×10=40π(cm2).方法总结:解题时要明确侧面积的计算方法,即圆柱侧面积=底面周长×圆柱高.变式训练:见《学练优》本课时练习“课堂达标训练”第3题【类型二】 由三视图求几何体的表面积如图是两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个几何体的表面积.解析:先由三视图得到两个长方体的长,宽,高,再分别表示出每个长方体的表面积,最后减去上面的长方体与下面的长方体的接触面面积即可.解:根据三视图可得:上面的长方体长6mm ,高6mm ,宽3mm ,下面的长方体长10mm ,宽8mm ,高3mm ,这个几何体的表面积为2×(3×8+3×10+8×10)+2×(3×6+6×6)=268+108=376(mm 2).答:这个几何体的表面积是376mm 2.方法总结:由三视图求几何体的表面积,首先要根据三视图分析几何体的形状,然后根据三视图的投影规律—“长对正,高平齐,宽相等”,确定几何体的长、宽、高等相关数据值,再根据相关公式计算几何体的面积.注意:求解组合体的表面积时重叠部分不应计算在内.变式训练:见《学练优》本课时练习“课堂达标训练” 第4题【类型三】 由三视图求几何体的体积某一空间图形的三视图如图所示,其中主视图是半径为1的半圆以及高为1的矩形;左视图是半径为1的四分之一圆以及高为1的矩形;俯视图是半径为1的圆,求此图形的体积(参考公式:V 球=43πR 3).解析:由已知中的三视图,我们可以判断出该几何体的形状为下部是底面半径为1,高为1的圆柱,上部是半径为1的14球组成的组成体,代入圆柱体积公式和球的体积公式,即可得到答案.解:由已知可得该几何体是一个下部为圆柱,上部为14球的组合体.由三视图可得,下部圆柱的底面半径为1,高为1,则V圆柱=π,上部14球的半径为1,则V 14球=13π,故此几何体的体积为错误!.方法总结:由三视图求几何体的体积,首先要根据三视图分析几何体的形状,然后根据三视图的投影规律“长对正,高平齐,宽相等”确定几何体的长、宽、高等相关数据值.再根据相关公式计算几何体各部分的体积并求和.变式训练:见《学练优》本课时练习“课堂达标训练”第6题【类型四】由三视图确定几何体面积或体积的实际应用杭州某零件厂刚接到要铸造5000件铁质工件的订单,下面给出了这种工件的三视图.已知铸造这批工件的原料是生铁,待工件铸成后还要在表面涂一层防锈漆,那么完成这批工件需要原料生铁多少吨?涂完这批工件要消耗多少千克防锈漆(铁的密度为7.8g/cm3,1g防锈漆可以涂4m2的铁器面,三视图单位为cm)?解析:从主视图和左视图可以看出这个几何体是由前后两部分组成的,呈一个T字形状.故可以把该几何体看成两个长方体计算.解:∵工件的体积为(30×10+10×10)×20=8000cm3,∴重量为8000×7.8=62400(g)=62.4(g),∴铸造5000件工件需生铁5000×62.4=312000(g)=312(t).∵一件工件的表面积为2×(30×20+20×20+10×30+10×10)=2800cm2=0.28m2.∴涂完全部工件需防锈漆5000×0.28÷4=350(g).方法总结:本题主要考查了由三视图确定几何体和求几何体的面积;关键是得到几何体的形状,得到所求的等量关系的相对应的值.变式训练:见《学练优》本课时练习“课后巩固提升”第7题三、板书设计1.由三视图求几何体的侧面积;2.由三视图求几何体的表面积;3.由三视图求几何体的体积.本节重在引导学生总结解决此类问题的方法和规律,探究其实质.在小组讨论的过程中,学生了解了三视图中相关数据的对应关系,即“长对正,高平齐,宽相等”,找到了解决问题的根本,通过具体的例题,让学生进行练习,巩固学习效果.。
29.2 三视图第3课时由三视图确定几何体的面积或体积【学习目标】1、学会根据物体的三视图描述出几何体的基本形状或实物原型。
2、经历探索简单的几何体的三视图的还原,进一步发展空间想象能力进而求面积或体积。
3、了解将三视图转换成立体图形在生产中的作用,使学生体会到所学知识有重要的实用价值。
【学习重点】根据三视图描述基本几何体和实物原型及三视图在生产中的作用。
【学习难点】根据三视图想象基本几何体实物原型求面积或体积。
【学习过程】【问题情境】让学生欣赏事先准备好的机械制图中三视图与对应的立体图片,借助图片信息,让学生体会本章知识的价值。
并借此可以讲述一下现在一些中专、中技甚至大学开设的模具和机械制图专业的课程都需要这方面的知识,激发学生学习兴趣,导入本课。
【自主探究】根据下列几何体三视图,画出它们的表面展开图:(1解:(1)该物体是:(2)该物体是:画出它的展开图是:画出它的展开图是:【合作探究】例6某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积。
问题:要想救出每个密封罐所需钢板的面积,应先解决哪些问题?小组讨论结论:1、应先由三视图想象出物体的;2、画出物体的;解:该物体是:画出它的展开图是:它的表面积是:变式训练:如图,上下底面为全等的正六边形的礼盒,其主视图与左视图均由矩形构成,主视图中大矩形的边长如图所示,左视图中包含两个全等的矩形。
如果用彩色胶带如图包扎礼盒,所需胶带长度至少为( )A 、120cmB 、395.24cmC 、431.76cmD 、480cm【归纳总结】物体的形状、物体的三视图、物体的展开图三者相互联系、相互转化,我们可以由三构造几何原型,进而画出它的展开图,还可求表面积和体积等。
【合作探究】如图,一个空间几何体的主视图和左视图都是边长为1的三角形,俯视图是一个圆,那么这个几何体的侧面积是( )A 、41πB 、42πC 、22πD 、21π变式训练:如图是一个几何体的三视图:(1) 写出这个几何体的名称;(2) 根据所示数据计算这个几何体的表面积;(3) 如果一只蚂蚁要从这个几何体中点B 出发,沿表面爬行到AC 的中点D ,请求出这个路线的最短路程。
29.2 三视图第3课时由三视图确定几何体的面积或体积【学习目标】1、学会根据物体的三视图描述出几何体的基本形状或实物原型。
2、经历探索简单的几何体的三视图的还原,进一步发展空间想象能力进而求面积或体积。
3、了解将三视图转换成立体图形在生产中的作用,使学生体会到所学知识有重要的实用价值。
【学习重点】根据三视图描述基本几何体和实物原型及三视图在生产中的作用。
【学习难点】根据三视图想象基本几何体实物原型求面积或体积。
【学习过程】【问题情境】让学生欣赏事先准备好的机械制图中三视图与对应的立体图片,借助图片信息,让学生体会本章知识的价值。
并借此可以讲述一下现在一些中专、中技甚至大学开设的模具和机械制图专业的课程都需要这方面的知识,激发学生学习兴趣,导入本课。
【自主探究】根据下列几何体三视图,画出它们的表面展开图:(1解:(1)该物体是:(2)该物体是:画出它的展开图是:画出它的展开图是:【合作探究】例6某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积。
问题:要想救出每个密封罐所需钢板的面积,应先解决哪些问题?小组讨论结论:1、应先由三视图想象出物体的;2、画出物体的;解:该物体是:画出它的展开图是:它的表面积是:变式训练:如图,上下底面为全等的正六边形的礼盒,其主视图与左视图均由矩形构成,主视图中大矩形的边长如图所示,左视图中包含两个全等的矩形。
如果用彩色胶带如图包扎礼盒,所需胶带长度至少为( )A 、120cmB 、395.24cmC 、431.76cmD 、480cm【归纳总结】物体的形状、物体的三视图、物体的展开图三者相互联系、相互转化,我们可以由三构造几何原型,进而画出它的展开图,还可求表面积和体积等。
【合作探究】如图,一个空间几何体的主视图和左视图都是边长为1的三角形,俯视图是一个圆,那么这个几何体的侧面积是( )A 、41πB 、42πC 、22πD 、21π变式训练:如图是一个几何体的三视图:(1) 写出这个几何体的名称;(2) 根据所示数据计算这个几何体的表面积;(3) 如果一只蚂蚁要从这个几何体中点B 出发,沿表面爬行到AC 的中点D ,请求出这个路线的最短路程。
29.2 三视图第3课时由三视图确定几何体的面积或体积1.能根据三视图求几何体的侧面积、表面积和体积等;(重点)2.解决实际生活中与面积、体积等方面有关的实际问题.(难点)一、情境导入已知某混凝土管道的三视图,你能根据三视图确定浇灌每段这种管道所需混凝土的体积吗(π=3.14)?二、合作探究探究点:由三视图确定几何体的面积或体积【类型一】由三视图求几何体的侧面积已知如图为一几何体的三视图:(1)写出这个几何体的名称;(2)若从正面看的长为10cm,从上面看的圆的直径为4cm,求这个几何体的侧面积(结果保留π).解析:(1)根据该几何体的主视图与左视图是矩形,俯视图是圆可以确定该几何体是圆柱;(2)根据告诉的几何体的尺寸确定该几何体的侧面积即可.解:(1)该几何体是圆柱;(2)∵从正面看的长为10cm,从上面看的圆的直径为4cm,∴该圆柱的底面直径为4cm,高为10cm,∴该几何体的侧面积为2πrh=2π×2×10=40π(cm2).方法总结:解题时要明确侧面积的计算方法,即圆柱侧面积=底面周长×圆柱高.变式训练:见《学练优》本课时练习“课堂达标训练”第3题【类型二】由三视图求几何体的表面积如图是两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个几何体的表面积.解析:先由三视图得到两个长方体的长,宽,高,再分别表示出每个长方体的表面积,最后减去上面的长方体与下面的长方体的接触面面积即可.解:根据三视图可得:上面的长方体长6mm ,高6mm ,宽3mm ,下面的长方体长10mm ,宽8mm ,高3mm ,这个几何体的表面积为2×(3×8+3×10+8×10)+2×(3×6+6×6)=268+108=376(mm 2).答:这个几何体的表面积是376mm 2.方法总结:由三视图求几何体的表面积,首先要根据三视图分析几何体的形状,然后根据三视图的投影规律—“长对正,高平齐,宽相等”,确定几何体的长、宽、高等相关数据值,再根据相关公式计算几何体的面积.注意:求解组合体的表面积时重叠部分不应计算在内.变式训练:见《学练优》本课时练习“课堂达标训练” 第4题【类型三】 由三视图求几何体的体积某一空间图形的三视图如图所示,其中主视图是半径为1的半圆以及高为1的矩形;左视图是半径为1的四分之一圆以及高为1的矩形;俯视图是半径为1的圆,求此图形的体积(参考公式:V 球=43πR 3).解析:由已知中的三视图,我们可以判断出该几何体的形状为下部是底面半径为1,高为1的圆柱,上部是半径为1的14球组成的组成体,代入圆柱体积公式和球的体积公式,即可得到答案.解:由已知可得该几何体是一个下部为圆柱,上部为14球的组合体.由三视图可得,下部圆柱的底面半径为1,高为1,则V 圆柱=π,上部14球的半径为1,则V 14球=13π,故此几何体的体积为错误!.方法总结:由三视图求几何体的体积,首先要根据三视图分析几何体的形状,然后根据三视图的投影规律“长对正,高平齐,宽相等”确定几何体的长、宽、高等相关数据值.再根据相关公式计算几何体各部分的体积并求和.变式训练:见《学练优》本课时练习“课堂达标训练”第6题【类型四】由三视图确定几何体面积或体积的实际应用杭州某零件厂刚接到要铸造5000件铁质工件的订单,下面给出了这种工件的三视图.已知铸造这批工件的原料是生铁,待工件铸成后还要在表面涂一层防锈漆,那么完成这批工件需要原料生铁多少吨?涂完这批工件要消耗多少千克防锈漆(铁的密度为7.8g/cm3,1kg防锈漆可以涂4m2的铁器面,三视图单位为cm)?解析:从主视图和左视图可以看出这个几何体是由前后两部分组成的,呈一个T字形状.故可以把该几何体看成两个长方体来计算.解:∵工件的体积为(30×10+10×10)×20=8000cm3,∴重量为8000×7.8=62400(g)=62.4(kg),∴铸造5000件工件需生铁5000×62.4=312000(kg)=312(t).∵一件工件的表面积为2×(30×20+20×20+10×30+10×10)=2800cm2=0.28m2.∴涂完全部工件需防锈漆5000×0.28÷4=350(kg).方法总结:本题主要考查了由三视图确定几何体和求几何体的面积;关键是得到几何体的形状,得到所求的等量关系的相对应的值.变式训练:见《学练优》本课时练习“课后巩固提升”第7题三、板书设计1.由三视图求几何体的侧面积;2.由三视图求几何体的表面积;3.由三视图求几何体的体积.本节重在引导学生总结解决此类问题的方法和规律,探究其实质.在小组讨论的过程中,学生了解了三视图中相关数据的对应关系,即“长对正,高平齐,宽相等”,找到了解决问题的根本,通过具体的例题,让学生进行练习,巩固学习效果.。
29.2 三视图
原创不容易,为有更多动力,请【关注、关注、关注】,谢谢!
古之学者必严其师,师严然后道尊。
欧阳修
第3课时由三视图确定几何体的面积或体积
【学习目标】
1、学会根据物体的三视图描述出几何体的基本形状或实物原型。
2、经历探索简单的几何体的三视图的还原,进一步发展空间想象能力进而求面积或体积。
3、了解将三视图转换成立体图形在生产中的作用,使学生体会到所学知识有重
要的实用价值。
【学习重点】根据三视图描述基本几何体和实物原型及三视图在生产中的作用。
【学习难点】根据三视图想象基本几何体实物原型求面积或体积。
【学习过程】
【问题情境】让学生欣赏事先准备好的机械制图中三视图与对应的立体图片,借助图片信息,让学生体会本章知识的价值。
并借此可以讲述一下现在一些中专、中技甚至大学开设的模具和机械制图专业的课程都需要这方面的知识,激发学生学习兴趣,导入本课。
【自主探究】根据下列几何体三视图,画出它们的表面展开图:
(1
解:(1)该物体是:(2)该物体是:
画出它的展开图是:画出它的展开图是:
【合作探究】例6某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的
面积。
问题:要想救出每个密封罐所需钢板的面积,
应先解决哪些问题?
小组讨论
结论:1、应先由三视图想象出物体的;
2、画出物体的 ;
解:该物体是:
画出它的展开图是:
它的表面积是:
变式训练:如图,上下底面为全等的正六边形的礼盒,其主视图与左视图均由矩形构成,主视图中大矩形的边长如图所示,左视图中包含两个全等的矩形。
如果用彩色胶带如图包扎礼盒,所需胶带长度至少为()
A、120cm
B、395.24cm
C、431.76cm
D、480cm
【归纳总结】物体的形状、物体的三视图、物体的展开图三者相互联系、相互转化,我们可以由三构造几何原型,进而画出它的展开图,还可求表面积和体积等。
【合作探究】如图,一个空间几何体的主视图和左视图都是边为1的三角形,俯视图是一个圆,那么这个几何体的侧面积是( )
A 、41π
B 、42π
C 、22π
D 、2
1π
变式训练:如图是一个几何体的三视图:
(1) 写出这个几何体的名称;
(2) 根据所示数据计算这个几何体的表面积;
(3) 如果一只蚂蚁要从这个几何体中点B 出发,沿表面爬行到AC 的中点D ,
请求出这个路线的最短路程。
【归纳总结】根据物体的三视图想象物体的
形状一般是由俯视图确定物体在平面上的形
状.然后再根据左视图、主视图嫁接出它在空
间里的形状,从而确定物体的形状.
【学以致用】
(1)一个几何体的三视图如图所示,那么这
个几何体的侧面积是( )
A 、4π
B 、6π
C 、8π
D 、12π
(2)一个几何体的三视图如所示(其中标注的a、b、c为相应的边长),则这个
几何体的体积是()
2、如图是一个由干个棱长相等的正方体构成的几何体的三视图。
(1)请写出构成这个几何体的正方体的个数;
(2)请根据图中所示的尺寸,计算这个几何体的表面积。
【布置作业】教材P100 练习题
【素材积累】
1、只要心中有希望存摘,旧有幸福存摘。
预测来的醉好方法,旧是创未来。
坚志而勇为,谓之刚。
刚,生人之德也。
美好的生命应该充满期待、惊喜和感激。
人生的胜者决不会摘挫折面前失去勇气。
2、我一直知道,漫长人生中总有一段泥泞不得不走,总有一个寒冬不得不过。
感谢摘这样的时候,我遇见的世界上最美的心灵,我接受的最温暖的帮助。
经历过这些,我将带着一颗感恩和勇敢的心继续走上梦想的道路,无论是风雨还是荆棘。