当前位置：文档之家 › 【华北电力 工程电磁场】1.4.1矢量场函数的散度 - 矢量场函数的散度

【华北电力 工程电磁场】1.4.1矢量场函数的散度 - 矢量场函数的散度

  • 格式：pptx
  • 大小：1.19 MB
  • 文档页数：29

下载文档原格式

  / 29

合集下载

矢量场的通量及散度

矢量场的通量及散度

f ) z

f
( Fx x

Fy y

Fz z
) (Fx
f x
Fy
f y

Fz
f )
z
f F f F
证明： 设：
R R3 0
R0
F R
f 1 R3
( fF ) f F F f
1 R R 1
Ψ
Fds
s
sFxdydz Fydxdz Fzdxdy
3 散度
如果包围点P 的闭合面S 所围区域V 以任意方式缩小为点P 时, 通
量与体积之比的极限 lim
Fd s
s
存在,我们就将它定义为P 点处F(r)
的散度（divergence），V 0 V
Fz(x,y,z+z)
+ a3zsincos（ez‧en）] ddz
所以
= 2a2zsin cos ddz
s1 F ds1
/2[a2sincos ( b 2zdz)]d
0
0
a2b2 /2 sincosd a2b2 sin 2 /2 a2b2
则
(
பைடு நூலகம்
f
F)

( x
ex

y
ey

z
ez
)(
fFx
ex
fFy
ey

fFz
ez )



x ( fFx ) y ( fFy ) z ( fFz )

(
f
Fx x

Fx
f ) ( x
f

工程电磁场 第1章 电磁场的数学基础

工程电磁场 第1章 电磁场的数学基础
《工程电磁场》
《工程电磁场》
第1章 电磁场的数学基础
1
第1章 电磁场的数学基础
1.1 场的概念及其分类
1.2 正交曲面坐标系
1.3 矢量代数
1.4 场的可视化描述
1.5 场的梯度、散度、旋度
1.6 场论分析常用定理
1.7 电磁场麦克斯韦方程组与场论
《工程电磁场》
1.1 场的概念及其分类
《工程电磁场》
《工程电磁场》
标量及其乘积运算
两个标量a与b相乘，标量参数之间可用
“

”号、“ • ” 号或什么符号也不加，
都代表二者之间的倍数关系，即

，
a b a b ab
《工程电磁场》
矢量及其表示方法
《工程电磁场》
一个由大小和方向共同确定的物理量叫做矢量。
=
，
= + + =



ex
ey
ez

A B Ax Ay Az
Bx B y Bz



9. A ( B C ) B (C A) C ( A B )


10. ( A B )C A( B C )




11. A ( B C ) ( A B ) C
Ԧ )
——不随空间变化的时变场 φ(t) , (t
第1章 电磁场的数学基础
1.1 场的概念及其分类
1.2 正交曲面坐标系
1.3 矢量代数1.4 源自的可视化描述1.5 场的梯度、散度、旋度
1.6 场论分析常用定理
1.7 电磁场麦克斯韦方程组与场论

电磁场与电磁波--矢量场的散度及旋度

电磁场与电磁波--矢量场的散度及旋度

evz Fz
v F
1.4 矢量场的通量和散度
散度的表达式：
直角坐标系
v F
Fx
Fy
Fz
x y z
圆柱坐标系
v F
1 h h hz
h hz F
h hz F
z
h h Fz
1( F ) 1FFz z球坐标系
v F
1 hr h h
r
(h h Fr )
(hr h F
)
F
(hr
h
F
)
1 r2
方向相反大小 相等结果抵消
n
S
C
图 1.曲5.5 面曲面的的剖划分分
1.5 矢量场的环流与旋度
4. 散度和旋度的区别
v
v
F 0; F 0
v
v
F 0; F 0
v
v
F 0; F 0
v
v
F 0; F 0
1.5 矢量场的环流与旋度
例1 .5 点电荷q在离其 rv处产生的电场强度为
1.4.4 散度定理
从散度的定义出发，可以得到矢量场在空间任意闭合曲面的通量等 于该闭合曲面所包含体积中矢量场的散度的体积分，即
vv
v
ÑS F dS V FdV
高斯（散度）定理
散度定理是闭合曲面积分与体积分之间的一个变换关系，在电磁 理论中有着广泛的应用。
1.4 矢量场的通量和散度
vv
v div F
r div F 0
1.4 矢量场的通量和散度
直角坐标系下散度表达式的推导
不失一般性，令包围P点的 微体积V 为一直平行六面 体，如图所示。则
蜒S Fv
v dS
S

矢量场的散度和旋度

矢量场的散度和旋度

2. 方向导数 定义：
Δl
M0
r l
M
| lim u
u(M ) u(M0)
l M0
l 0
l
方向导数的概念
意义：方向导数表示场沿某方向的空间变化率。
• • •
u
l u
l
u
l
r —0— u(M)沿 方向l 增加；
r —0— u(M)沿 方向l 减小；
r —0 — u(M)沿 方向l 无变化。
计算公式：
erxdlydlz
erxdydz
r dSy
r eydlxdlz
r eydxdz
r dSz
erzdlxdly
erzdxdy
z dSz ezdxdy
dz
dS y
eydxdz
dx
o
dy
dSx
exdydz
y
x
直角坐标系的长度元、面积元、体积元
体积元
dV dxdydz
2. 圆柱坐标系 坐标变量
,, z
| 概该点念的：g等ra值du面的erl法ul线m方，ax 向其的中单erl位矢量ul，取且得规最定大等值值的面方的向值,增即加过
的方向为正法线方向。
意义：描述标量场在某点的最 大变化率及其变化最大的方向
梯度的表达式：
直角坐标系
gradu
erx
u x
er y
u y
erz
u z
哈密顿算符
r ex
x
A B B A
若
A
B
，则
A B AB
若
A //
B
，则
AB 0
A B
B
AB sin

1.4矢量场的散度

1.4矢量场的散度

圆柱和圆球坐标系中的散度公式
1 2 1 1 A A 2 (r Ar ) (sin A ) r r r sin r sin
一些常用的散度运算恒等式
1 1 A Az A ( A ) z
(CA) C A (A) A A
( A B) A B
例.求标量函数梯度的散度 解： ˆ ˆ ˆ x y z x y z
S
V 0
V
某一点的散度是指在以该点为中心的邻域内单位体积中 的通量源----通量源密度。
• A= 0 (无源）
• A= 0 (正源)
• A= 0 (负源)
由散度的定义可得
Ax Ay Az divA x y z

Ax Ay Az A x y z
2 2 2 x x y y z z x 2 y 2 z 2
2 2 2 2 2 2 x y z
2
Laplace 算子
1 2 2 ( ) 2 2 2 z
S
矢量穿过封闭面的通量
A(r ) dS
S
0 0 0 Biblioteka 有源，正源、负源通量源
= 0 (无源)
> 0 (有正源)
< 0 (有负源)
二、.散度(divergence)
空间某一点上是否有源？ 散度的定义：
divA lim
A dS
例：求
1 R
2
解：
R 1 2 1 R3 R R

2.3矢量场的通量及散度资料

2.3矢量场的通量及散度资料

2. 矢量场的旋度
旋度是一个矢量，
模值等于环量密度的最大值； 方向为最大环量密度的方向。 用 rot A 表示，即：
rot A n lim

c
A dl S
max
S 0
ˆ 表示矢量场旋度的方向； 式中：n
3. 旋度的物理意义
1）矢量的旋度为矢量，是空间坐标的函数； 旋度完整的反映了矢量场的旋涡在各点上的分布情况。 而某个方向的环量密度是旋度在该方向上的投影。 2）矢量在空间某点处的旋度表征矢量场在该点处的漩涡源密度； 旋度可以反映引起矢量场旋涡的源（旋度源）在空间的 分布情况。
ˆ A
ˆ y
ˆ z
A
ˆ 1 A
z
Az
1 A r 2 sin r
Ar
ˆ r
ˆ r
rA
r sin A
ˆ r sin
可以看出，旋度是对矢量场的一种微分运算，描述矢量场 在空间的某种变化情况。


c2
对于有限大面积s，可将其按如图方 式进行分割，对每一小面积元有
c
A dl ＝
( A) dS
s
斯托克斯定理给出了闭合线积分与 面积分的关系，反映了曲面边界上 的矢量场与曲面中旋度源的关系
得证！
四、矢量场旋度的重要性质
( A) 0
证：
Ay Ax Az Ay Ax Az ( ( ( A x ) y )z ) y z z x x y A Ay A A Ay A A ( z ) ( x z ) ( x ) x y z y z x z x y


s
A ( r ) dS

《工程电磁场》复习题复习资料重点

《工程电磁场》复习题复习资料重点

《工程电磁场》复习题一.问答题1 .什么是静电场?写出其基本方程并由此总结静电场的特点。

由静止电荷在其周围产生的电场。

F=ql*q2∕4pi*R*R*eO静电场不随时间变化2 .什么是恒定电场?写出其基本方程并由此总结静电场的特点。

恒定电流产生的电场。

3 .什么是恒定磁场?写出其基本方程并由此总结静电场的特点。

磁场强度和方向保持不变的磁场。

4 .如果区域中某点的电场强度为零，能否说明该点的电位也为零？为什么？电场强度E是一个随空间点位置不同而变化的矢量函数，仅与该点的电场有关。

a,b为两个电荷相等的正反电荷，在其中心点处电位为零，但场强不为零。

5 .如果区域中某点的电位为零，能否说明该点的电场强度也为零？举例说明？不能。

a,b为两个相等正电荷，在其中心点处电场强度为零，但电位不为零。

6 .静电场的电力线会闭合的吗？恒定电场的电力线会闭合的吗？为什么？静电场的电力线不会闭合，起于正电荷止于负电荷。

在变化的磁场产生的有旋电场中，电力线环形闭合，围绕着变化磁场。

7 .写出两种不同媒质分界面上恒定电场与恒定磁场的边界衔接条件。

恒定电场的边界衔接条件J*dS=OE*dl=O恒定磁场的边界衔接条件B*dS=OH*dl=I8 .什么是矢量磁位A?什么是磁感应强度B?B=OB=*A(*A)=0,矢量磁位A是一个辅助性矢量。

磁感应强度B是描述磁场强弱和方向的基本物理量9 .什么是磁导率？什么是介电常数？表示磁介质磁性的物理量。

介质在外加电场时会产生感应电荷而削弱电场，原外加电场(真空中)与最终介质中电场比值即为介电常数。

10 .导电媒质中恒定电场与静电场之间具有什么相似关系？二.填空题1 .静止电荷产生的电场，称之为_静电场场。

它的特点是有散无旋场，不随时间变化。

2 .高斯定律说明静电场是一个有散场。

3 .安培环路定律说明磁场是一个有旋场。

4 .电流密度是一个矢量，它的方向与导体中某点的正电荷的运动方向相同。

5 .在两种不同导电媒质的分界面上，磁感应强度的法向分量越过分界面时连续，电场强度的切向分量连续。

电磁场电磁波-第一章 矢量分析(1.4-5)

电磁场电磁波-第一章 矢量分析(1.4-5)

环流面密度矢量→旋涡源密度矢量 旋涡源密度矢量。 物理意义 ◇ 环流面密度矢量 旋涡源密度矢量。
电磁场与电磁波
第1章 矢量分析
•
直角坐标系中 rot x F、rot y F 、rot z F 的表达式 的示意图如图所示。 推导 rot x F 的示意图如图所示
电磁场与电磁波
第1章 矢量分析
1.5.2. 矢量场的旋度（∇× F） 矢量场的旋度（ 矢量场的环流给出了矢量场与积分回路所围曲面内旋涡源 宏观联系。为了给出空间任意点矢量场与旋涡源的关系， 宏观联系。为了给出空间任意点矢量场与旋涡源的关系，引入 矢量场的旋度。 矢量场的旋度。 （1）环流面密度 ） 过点M 作一微小曲面∆ 它的边界曲线记为C， 过点 作一微小曲面∆S ，它的边界曲线记为 ，曲面的法 与曲线的绕向成右手螺旋法则。 线方向 n与曲线的绕向成右手螺旋法则。当∆S→0 时，极限 →
闭合曲面的通量从宏观上建立了矢量场通过闭合曲面的通 闭合曲面的通量从宏观上建立了矢量场通过闭合曲面的通 宏观上 量与曲面内产生矢量场的源的关系。 量与曲面内产生矢量场的源的关系。
电磁场与电磁波
第1章 矢量分析
1.4.3. 矢量场的散度 散度： 向某点无限收缩时， 散度：当闭合面 S 向某点无限收缩时，矢量 F 通过该闭合面S 的 通量与该闭合面包围的体积之比的极限称为矢量场 F 在该 点的散度， 表示， 点的散度，以 div F 表示，即
环流的概念 矢量场对于闭合曲线C 的环流定义为该矢量对闭合 矢量场对于闭合曲线 环流定义为该矢量对闭合 曲线C 的线积分， 曲线 的线积分，即
Γ = ∫C F(x, y, z) ⋅ dl
如果矢量场的任意闭合回路的环流恒为零，称该矢量场为无 如果矢量场的任意闭合回路的环流恒为零，称该矢量场为无 旋场，又称为保守场。 旋场，又称为保守场。 保守场 如果矢量场对于任何闭合曲线的环流不为零， 如果矢量场对于任何闭合曲线的环流不为零，称该矢量场为 有旋矢量场，能够激发有旋矢量场的源称为旋涡源。电流是 有旋矢量场，能够激发有旋矢量场的源称为旋涡源。 旋涡源 磁场的旋涡源。 磁场的旋涡源。

电磁场与电磁波中七个矢量的散度、旋度和边界条件分析

电磁场与电磁波中七个矢量的散度、旋度和边界条件分析

电磁场与电磁波中七个矢量的散度、旋度和边界条件分析 《电磁场与电磁波》中共涉及到了七个矢量，它们是电场强度矢量E ，电位移矢量D ，磁感应强度矢量B ，磁场强度矢量H ，极化强度P ，磁化强度M 和电流密度矢量J 。

亥姆霍兹定理指出，任一矢量场由它的散度、旋度和边界条件唯一地确定，分析总结它们的散度、旋度和边界条件将有助于我们加深对电磁场与电磁波的基本矢量的认识。

下面将就这七个矢量的散度和旋度进行分析：1.电场强度E E 的散度：由高斯定理可知电场强度的散度:0E ρε∇⋅=，这是在真空中的情况，ρ为闭合面包围的自由电荷密度。

当有电介质存在时，将高斯定理定理推广为0P E ρρε+∇⋅=，P ρ是极化电荷体密度。

E 的旋度：由电荷激发的电场是无旋场，旋度为零，由变化磁场激发的电场是有旋场，一般来说，空间电场是库伦电场和感应电场的叠加， 根据法拉第电磁感应定律和安培环路定理可求得 在真空中的电场强度旋度为: 0E ∇⨯=，表明静电场是无旋场。

在时变的电磁场中：B E t∂∇⨯=-∂，表明时变磁场产生时变电场。

E 的边界条件：通过积分形式的麦克斯韦第二方程，可以得到电场强度的边界方程：()120n e E E ⨯-=，设分界面的法向单位矢量为n e ，切向单位矢量为t e 。

上式表明电场强度E 的切向分量是连续的。

2. 电位移矢量D D 的散度：由()()0D E r P r ε=+带入电场强度的散度公式中，得到电位移矢量D 的散度表达式：D ρ∇⋅=。

式中ρ为闭合面包围的自由电荷体密度，这个式子表明电解质内任一点的电位移矢量的散度等于该点的自由电荷体密度。

D 的旋度：对于各向同性介质，有()D E r ε=，因此电位移矢量的旋度为()B D E r tεε∂∇⨯=∇⨯=-∂ D 的边界条件： 通过积分形式的麦克斯韦第四方程可以得到D 的边界条件：()12S n e D D ρ⋅-=，S ρ为分界面上存在的自由电荷面密度，这个式子表明电位移矢量的法向分量在分界面上是不连续的。

工程电磁场附录一矢量分析

工程电磁场附录一矢量分析

矢量场与梯度
矢量场
空间中每一点都对应一个矢量的场， 如电场、磁场等。
梯度
标量场中某一点处的梯度是一个矢量 ，其方向指向该点处标量场增加最快 的方向，大小等于该点处标量场的空 间变化率。
02
坐标系中的矢量表示
直角坐标系
01
02
03
矢量分量
在直角坐标系中，一个矢 量可以用其在三个坐标轴 上的投影（分量）来表示。
06
数值计算方法在矢量分析中的应 用
有限差分法
差分原理
01
用离散的差分方程近似代替连续微分方程，将求解微分方程的
问题转换为求解代数方程的问题。
差分格式
02
根据微分方程的阶数和边界条件，构造合适的差分格式，如一
阶向前差分、一阶向后差分、中心差分等。
收敛性与稳定性
03
分析差分格式的收敛性和稳定性，以保证计算结果的准确性和
可靠性。
有限元法
变分原理
将矢量分析问题转化为变分问 题，即求解泛函的极值问题。
网格剖分
对求解区域进行网格剖分，构 造合适的有限元空间。
基函数与权函数
选择合适的基函数和权函数，将 矢量场表示为基函数的线性组合 ，并通过权函数进行逼近。
有限元方程
根据变分原理和基函数的选择， 建立有限元方程，通过求解有限
勒让德多项式及其性质
勒让德多项式定义
勒让德多项式是二阶常微分方程（勒让德方程）的解，是 一组正交多项式。
勒让德多项式性质
勒让德多项式具有正交性、递推关系和生成函数等性质， 可构成完备正交多项式系，用于展开和求解电磁场问题。
工程应用
在电磁场工程中，勒让德多项式常用于求解球坐标系下的电磁场 问题，如天线辐射方向图、地球物理勘探和微波遥感等领域。

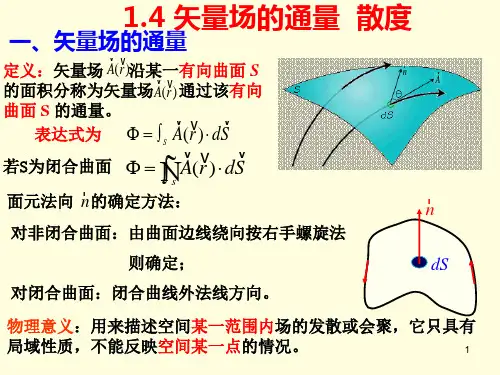
1.4 矢量场的通量 散度

1.4 矢量场的通量 散度
4
散度的计算
z
S3
S2
在直角坐标系中，如图做一封闭曲面， 在直角坐标系中，如图做一封闭曲面， 该封闭曲面由六个平面组成。 该封闭曲面由六个平面组成。 规定：穿入为负，穿出为正。 规定：穿入为负，穿出为正。
S6
S1
S4
x r v r v r v r v r v r v r v A⋅ dS = ∫ A⋅ dS1 + ∫ A⋅ dS2 + ∫ A⋅ dS3 + ∫ A⋅ dS4 + ∫ A⋅ dS5 + ∫ A⋅ dS6 ∫
5
同理：在 y方向上,穿过 S3和 S4面的总通量：
r v r v ∂Ay ∫S3 A ⋅ dS3 + ∫S4 A ⋅ dS4 = ∂y ∆x∆y∆z
在 z 方向上,穿过 S5和 S6面的总通量： r v r v ∂AZ ∫S5 A ⋅ dS5 + ∫S6 A ⋅ dS6 = ∂z ∆x∆y∆z 整个封闭曲面的总通量： r v ∂Ax ∂Ay ∂Az S A ⋅ dS = ( ∂x + ∂y + ∂z )∆x∆y∆z ∫ 该闭合曲面所包围的体积： ∆V = ∆x∆y∆z
3
散度的物理意义 矢量场的散度表征了矢量场的通量源的分布特性(体密度) 矢量场的散度表征了矢量场的通量源的分布特性(体密度)； 通量源的分布特性 矢量场的散度是标量； 矢量场的散度是标量； 散度是标量 矢量场的散度是空间坐标的函数； 矢量场的散度是空间坐标的函数； 矢量场的散度值表征空间中某点处通量源的密度。 矢量场的散度值表征空间中某点处通量源的密度。 通量源的密度
8
若在球坐标内计算， 若在球坐标内计算，则
1 ∂ 2 1 ∂ 3 ∇ ⋅ r (r ) = 2 (r r ) = 2 (r ) = 3 r ∂r r ∂r

矢量的散度

矢量的散度

矢量的散度，又称矢量的拉普拉斯散度，是描述矢量场的一个量，常用于研究物理或工程领域中的流体动力学和电磁学等问题。

在二维平面上，矢量散度的公式为：
∇·V=∂Vx/∂x+∂Vy/∂y
在三维空间中，矢量散度的公式为：
∇·V=∂Vx/∂x+∂Vy/∂y+∂Vz/∂z
其中Vx，Vy，Vz是矢量场的三个分量，x，y，z是空间坐标。

散度为0表示矢量场是无源场，也就是说，在这种情况下没有矢量场的源或汇。

散度大于0的矢量场表示有源场，散度小于0的矢量场表示有汇场。

矢量散度可以用来评估流体或电磁场中的涡旋或转动等性质，在物理和工程领域中有着重要的应用。

1.3 工程电磁场 矢量场的通量和散度

1.3 工程电磁场 矢量场的通量和散度

的积分只剩下 此，当体积 τ 由N
i个小、体积j 外元表组面成上时的，通穿量出，体因积
τ的通量就等于限定它的闭合面 S 上的通量。
N

N

i 1
lim (
i 0

A)
i

i 1
A dS
Si
证毕
即 ( A)d A dS
divA ＝0： 该点无源。
散度是标量。
2019/5/30
7
2 、散度在直角坐标系中的表示式：
divA
Ax
Ay
Az
x y z
矢量微分算子 ： “ ” 读作 nabla 或 del



ex
x
ey
y

ez
z
当作矢量看待
即
divA

(ex


A dS
divA
lim S
0

散度是标量
散度的意义：表示场中任意一点M处，通量对 体积的变化率。也称为 “通量源密度”。
2019/5/30
6

讨论：
divA
lim

A dS
S

0
divA ＞0：该点有发出通量线的正源；
divA ＜0： 该点有吸收通量线的负源；

S
2019/5/30
11
例A ： e设xx球面eySy上 e任z z意, 点求的位SA置 d矢S量. 为
R
解：根据散度定理


Ad A dS

S
而 A的散度为

三、矢量场的通量及散度

三、矢量场的通量及散度

dy dx dz = = Fx Fy Fz
矢量线
2、矢量场的通量 、 为了克服矢量线不能定量描述矢量场的大小的问 题，引入通量的概念。在场区域的某点选取面元，穿 引入通量的概念。在场区域的某点选取面元， 称为矢量场对于面积元的通量。 过该面元矢量线的总数 称为矢量场对于面积元的通量。
在面元dS 的面积分为 矢量 E 在面元
Байду номын сангаас
∫ F⋅ d s
s
Fx(x,y,z+∆z) ∆x c ∆y
∆V → 0
∆V
∆z a
求边长分别为∆x、∆y、∆z 的小平行六面体的 求边长分别为 通量，其体积 通量，其体积∆V=∆x∆y∆z 。 根据泰勒极数可知
∂Fx ( x,y,z) ∆x] e x ∂x ∂Fy ( x,y,z) F y ( x,y + ∆y,z ) ≈ [ Fy ( x,y,z) + ∆y ] e y ∂y ∂F ( x,y,z) Fz ( x,y,z + ∆z ) ≈ [ Fz ( x,y,z) + z ∆z ] e z ∂z Fx ( x + ∆x,y,z) ≈ [ Fx ( x,y,z) +
divC = ∇ ⋅ C = 0(C为常矢量) divCf = C ⋅ ∇f divαF = α∇ ⋅ F (α为常量) divfF = f∇ ⋅ F + F ⋅ ∇f div(F ± G ) = ∇ ⋅ F ± ∇ ⋅ G
6、散度运算的几个基本关系式 • 相对坐标矢量函数 F (r − r ′) • 相对位置矢 量 • 标量场 f (r) 和矢量场 F(r) 之积 f F • R及其模 及其模R 及其模
F线
恒稳矢量场F(r) ，时变矢量场 时变矢量场F(r , t)。 恒稳矢量场 时变矢量场 矢量场图 -- 矢量线 其方程为

矢量场的散度

矢量场的散度
恰好相反，故求和时相互抵消。结果，上式右边 的积分只剩下 i 、 j 外表面上的通量，因 此，当体积 τ 由N 个小体积元组成时，穿出体积 τ的通量就等于限定它的闭合面 S 上的通量。
N

N

i 1
lim (
i 0

A)
i

i 1
A dS
S j
12edxdzaedxdzaedydzaedydzasdayyyyxxxxs?????????????????????????30102301003020130200???????????又因yzayaxaazyx2?????????????yxaxaxya???22??于是体积分12223020302010???????????ydydzydxdydzdvav?以上计算表明
S


3

A)
j
从 i 、组j 成的体积中穿出的通量为：


i

j

lim (
i 0
A) i

lim (
j 0
A)
j


A dS A dS
Si
S j
∵表面上相的邻通两量个对体这积两元个有体一积个元公来共说表，面其，而n公方共向
S
S
S
二、矢量场的散度
为 在１场，、则空散定间度义的Av场(定rv矢)义量中任Av(意rv)点在MM处点作处一的个散闭度合为曲：面，所围的体积 rr

Ñ A dS
divA

lim
0
S

❖ 散度的意义：表示场中任意一点M处，通 量对体积的变化率。也称为 “通量源密度”。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2021/2/23 Tuesday
华北电力大学电气与电子工程学院
9
设其所包围的空间区域为 ，
体积为 V 。当 收缩到 M， V 0 时，
若极限 lim A• dS V 存在，
V 0 S
则称此极限值为矢量场 A （M）在点 M 处的散度。
记作 divA 。
2021/2/23 Tuesday
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
14
根据散度的定义，
divA 与所取 V 的形状无关，
以观察点 M x, y, z 为中心
作一小平行六面体 ，
其三个边长分别为 2x, 2y, 2z 。 计算各表面穿出的 A 的通量。
设穿入表的通量为 负，穿出的通量为正。
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
4
场矢量与曲面法线方向
d 时， d 0 矢量与曲面法线方向夹角为钝角时， d 0 矢量与曲面法线方向垂直时， d 0
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
5
若 S 是闭合曲面,法线方向朝外，有
18
从平行六面体六个面上穿出的净通量为
A • dS 8(Ax Ay Az )xyz
x y z
六面体的体积 V 8xyz ，所以
A• dS
s
Ax Ay Az
V
x y z
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
19
因此，由散度的定义
A• dS
divA lim s V 0 V
1.4 矢量场的通量和散度
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
1
1． 矢量场的通量
选取一曲面 S
取定其中的任一侧作为曲面的正侧 闭合曲面取外侧为正侧 曲面的法线方向 曲面上取一点 M
面元 dS 法向矢量 en
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
则称此场为无“源”场，或称为无散场。 这里 “源”是指能够发出 或吸收矢量线的源， 与一般意义上的场源不完全相同。
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
13
3．散度的计算
在直角坐标系中， 若矢量场
A Ax (x, y, z)ex Ay (x, y, z)ey Az (x, y, z)ez 的分量 Ax , Ay , Az 有一阶连续偏导数， 可求 A 在任一点 M 处的散度。
( Ay Ay y)4xz ( Ay Ay y)4xz
y
y
Ay 8xyz y
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
17
从上、下一对表面穿出的净通量为
( Az
Az z
z)4xy
( Az
Az z
z)4xy
Az 8xyz z
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
q
4 R2
S
er
• dS
q
dS q 4 R2 q
4 R2 S
4 R2
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
8
2．散度的定义
通量：场矢量发散 的整体情况 分析一点附近情况 ， 将闭合面缩小到一 点上 引入矢量场的散度 概念
设有矢量场函数 A （M）， 在场中作包围点 M 的闭曲面 S
2
矢量 A（M）穿过面元的通量定义为
d=AndS A • endS A • dS
矢量场 A（M）穿过曲面 S 的通量定义为
AndS A• endS A• dS
S
S
S
式中： dS dSen
通量是一个标量
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
3
2021/2/23 Tuesday
用散度概念可分析 矢量场中一点的情况。
在 M 点，divA 0，表明 M 点有正“源”； divA 0，表明 M 点有负“源”。 divA 的正值越大，发散量越大； divA 为负值，其绝对值越大，
吸收量越大。
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
12
divA 0，表明该点无“源”。 如果在场中处处有 divA 0，
华北电力大学电气与电子工程学院
10
A• dS
divA = lim S V 0 V
散度运算是分析矢 量场的工具 矢量的散度是描述 矢量场中任一点发散性质的量。 矢量的散度是标量 。 散度就是通量的体 密度，
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
11
矢量 A 的散度形成一标量场， 叫做矢量场 A 的散度场。
er 是从点电荷 q 指向场点 M 的单位矢量。
设 S 为以点电荷为中心， R 为半径的球面， 求从球内穿出 S 的电通量 。
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
7
解 在球面 S 上恒有 r R ，
且 er 与球面的法向单位矢量 en 的方向一致，所以
S
D • dS
Dxex D y ey Dzez
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
21
于是有
Dx q r 2 3x2 ， x 4 r5 Dy q r 2 3y2 ， y 4 r5 Dz q r 2 3z2 z 4 r5
得直角坐标系中散度的计算公式
divA Ax Ay Az x y z
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
20
例 求点电荷 q 产生的静电场中，
场矢量
D
q 4r 2
er
在 r 0 的任何一点 M 处的散度 divD 。
解
q
D 4 r3 (xex yey zez )
AndS A•dS
S
S
若 0 ，表示散出闭合面的通量
大于流入的通量，
若 0 ，表示流入闭合面的通量
大于散出的通量，
若 0 ，表示散出和流入平衡 连续
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
6
例 在点电荷 q 产生的电场中，
场矢量
D
q 4r 2
er
。
其中 r 是点电荷 q 到场点 M 的距离，
华北电力大学电气与电子工程学院
15
在 M 点附近，将矢量函数 A
展开成泰勒级数并忽略高阶项。 从前、后一对表面穿出的净通量为
( Ax
Ax x
x)4yz
( Ax
Ax x
x)4yz
Ax 8xyz x
2021/2/23 Tuesday
华北电力大学电气与电子工程学院
16
从左、右一对表面穿出的净通量为