1-2矢量场的散度

ei ej i Aj i Aj
i Ai i Ai
A A
19
五、斯托克斯公式与矢量场的旋度 矢量场的环量（环流）
图 2-4 矢量场的环量 20
21
矢量场的环量（环流）
环量 = 平均切向分量 X 绕行距离
矢量 A 沿任一闭合曲线 L 的积分称为环量 A dl L
0 表明在区域内无涡旋状态，场线不闭合
势函数。
2. 正定理: 矢量场的旋度必为无源场，即 A 0
逆定理: 无源场必可表示为某个矢量场的旋度。
即若 B 0 ，则 B A ， A 称为无源场 B
的矢量势函数。
26
亥姆霍兹定理
任意矢量场 F（ F 0, F 0 ）均可分
解为无旋场 F1 和无源场 F2 之和。
即 F 可分解为 F F1 F2 ( F1 0, F2 0 ) 。
Ay z
y
Az
z
Ay
A A
x
x
A A ex A ey A ez A x ex
A A
25
六、有关场的四个定理
关于散度旋度的两个定理 1. 正定理：标量场的梯度必为无旋场， 即 =0
逆定理：无旋场必可以表示为某一标量场的梯度。
即若 A 0 ，则 A ， 称为无旋场 A的标量
学校受教育。
干基本定理作出严格证明。
29
ex
x
ey
y
ez
z
( ) 9
例2： ( ) =？
解2 ：
( ) eii ( ) ei (i) ei (i )
( )
10
四、高斯定理与矢量场的散度
矢量族
在矢量场中对于给定的一点，有一个方向，它 沿某一曲线的切线方向，这条曲线形成一条矢 量线，又叫场线（对静电场称为电力线），无

定义向量场的散度，首先要引入通量的概念。

给定一个三维空间中的向量场以及一个简单有向曲面，则向量场通过曲面的通量就是曲面每一点上的场向量在曲面法向方向上的分量的积分:其中是积分的面积元，n是Σ在点(x,y,z)处的单位法向量。

如果曲面是封闭的，例如球面，那么通常约定法向量是从里朝外的，所以这时候的通量是描述曲面上的场向量朝外的程度。

通量描述了一定区域中向量场的方向趋势，散度则是这个性质的一种局部描述[1]:7-8。

某一点的散度是指包含这一点的某一个封闭曲面的通量除以封闭曲面围起来的微小体元的体积得到的比值在趋向于0时的极限：[2]:4如果用Nabla算子表示的话，向量场的散度记作：[2]:5从定义中可以看出，散度是向量场的一种强度性质，就如同密度、浓度、温度一样，它对应的广延性质是一个封闭区域表面的通量，所以说散度是通量的体密度[1]:7-8。

物理上，散度的意义是场的有源性。

某一点或某个区域的散度大于零，表示向量场在这一点或这一区域有新的通量产生，小于零则表示向量场在这一点或区域有通量湮灭。

这样的点或区域分别称为向量场的正源（发散源）和负源（洞）[1]:8。

举例来说，假设将太空中各个点的热辐射强度向量看做一个向量场，那么某个热辐射源（比如太阳）周边的热辐射强度向量都指向外，说明太阳是不断产生新的热辐射的源头，其散度大于零。

散度等于零的区域称为无源场或管形场。

流体力学中，散度为零的流体称为不可压缩流体，也就是说此流体中不会有一部分凭空消失或突然产生，每个微小时间间隔中流入一个微小体元的流体总量都等于在此时间间隔内流出此体元的流体总量。

在不同的坐标系下，向量场的散度有不同的表达方式。

直角坐标系在三维直角坐标系Oxyz中，设向量场的表示为[2]:8：，其中的分别是x轴、y轴、z轴方向上的单位向量，场的分量P、Q、R 具有一阶连续偏导数，那么向量场A的散度就是：圆柱坐标系圆柱坐标系中，假设物体的位置为，定义其径向单位矢量、横向单位矢量和纵向单位矢量为，那么向量场可以表示成：向量场A的散度就是[4][5]:73：球坐标系球坐标系中，假设物体的位置用球坐标表示为，定义它的基矢：，则向量场A可以表示成：向量场A的散度就是[6][5]:73：以下的性质都可以从常见的求导法则推出。

散度恒等于0 的矢量场，无通量源， 矢量线是无头无尾的闭合曲线。
电磁场与电磁波
第1章 矢量分析
场的概念—散度
求 A
例
ˆ （ A xy 2 x -10 x,y 10）
A
Ax Ay Az y2 x y z
电磁场与电磁波
第1章 矢量分析
场的概念—散度
对于静电场 E 而言： E r 正比于 r 点处 E 的通量源密度， 即 r 点处的电荷密度。
电磁场与电磁波
第1章 矢量分析
场的概念—散度
7.有源(散)场和无源(散)场：
• 有源场（有散场）：
散度值不为零的矢量场，存在通量源，
矢量线有端点。 •无源场(无散场)：
正交曲线坐标系中：
( Fu2 h1h3 ) ( Fu3 h1h2 ) 1 Fu1 h 2 h 3 F h1h2 h3 u1 u2 u3


电磁场与电磁波
第1章 矢量分析
场的概念—散度
6.散度的物理意义： Ar 正比于 r 点处 A 的通量源密度
Fx Fy Fz 直角坐标系中： F x y z
柱坐标系中： 球坐标系中：
1 ( Fr r ) 1 F Fz F r r r z
1 ( r 2 Fr ) 1 ( F sin ) 1 F F 2 r r r sin r sin
n2
F
n1
V2
F dS F dS F dS F dS F dS
S S1 S2 V1 V2
x
o y
对区域V=V1+V2的外闭合表面的 高斯积分等于对 V1 、 V2 的外闭 合表面高斯积分的代数和.

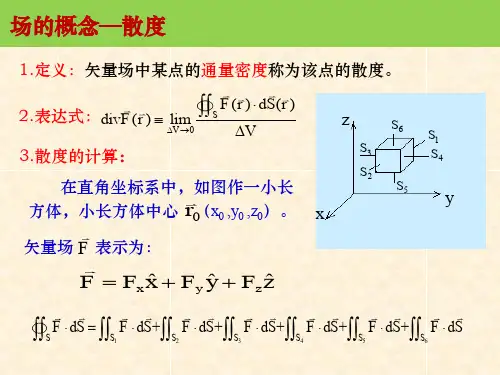
散度定理表达式
散度定理是高斯定理在物理中的实际应用，它经常应用于矢量分析中。

矢量场的散度在体积τ上的体积分等于矢量场在限定该体积的闭合曲面s上的面积分。

(附:散度定理是矢量场中体积分与面积分之间的一个变换关系在电磁场理论中非常有用)
表达式(为下图所示)
散度定理公式是∫∫（(əQ/əx)-(əP/əy)）dxdy。

散度定理又称为高斯散度定理、高斯公式，是指在向量分析中，一个把向量场通过曲面的流动（即通量）与曲面内部的向量场的表现联系起来的定理。

散度定理经常应用于矢量分析中。

矢量场的散度在体积τ上的体积分等于矢量场在限定该体积的闭合曲面s上的面积分。

在物理和工程中，散度定理通常运用在三维空间中。

然而，它可以推广到任意维数。

在一维，它等价于微积分基本定理；在二维，它等价于格林公式。

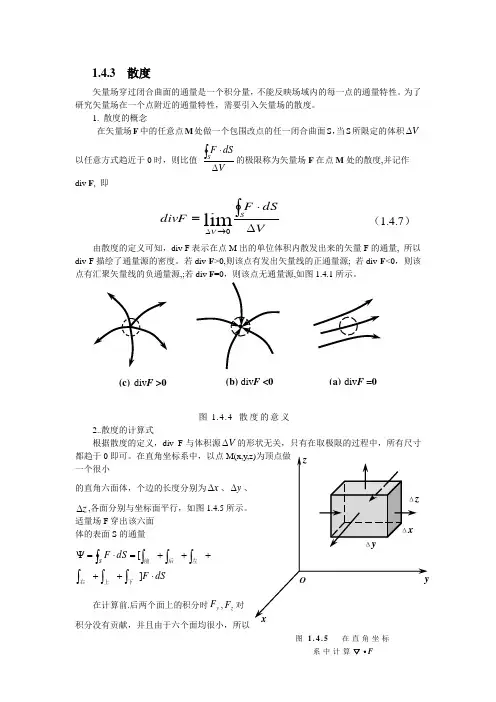
1.4.3 散度 矢量场穿过闭合曲面的通量是一个积分量，不能反映场域内的每一点的通量特性。为了研究矢量场在一个点附近的通量特性，需要引入矢量场的散度。 1. 散度的概念 在矢量场F中的任意点M处做一个包围改点的任一闭合曲面S，当S所限定的体积V

以任意方式趋近于0时，则比值 VdSFS的极限称为矢量场F在点M处的散度,并记作 div F, 即

VdSFdivFSV

lim0 （1.4.7）

由散度的定义可知，div F表示在点M出的单位体积内散发出来的矢量F的通量, 所以div F描绘了通量源的密度。若div F>0,则该点有发出矢量线的正通量源; 若div F<0，则该点有汇聚矢量线的负通量源,;若div F=0，则该点无通量源,如图1.4.1所示。

2..散度的计算式 根据散度的定义，div F与体积源V的形状无关，只有在取极限的过程中，所有尺寸都趋于0即可。在直角坐标系中，以点M(x,y,z)为顶点做 一个很小

的直角六面体，个边的长度分别为x、y、 z,各面分别与坐标面平行，如图1.4.5所示。

适量场F穿出该六面 体的表面S的通量

dSFdSFS][

下上右左后前

在计算前.后两个面上的积分时yF,zF对 积分没有贡献，并且由于六个面均很小，所以 图1.4.5 在直角坐标系中计算▽•F

O y x

z Δx Δy

Δz

(c) divF >0 (b) divF <0 (a) divF =0 图1.4.4 散度的意义 zyzyxxFdSFx),,(前

zyzyxFdSFx),,(后

根据泰勒定理

xxzyxFzyxFxxzyxFxxzyxFzyxFzyxxFxxxxxx),,(),,()(),,(21),,(),,(),,(222 所以 zyxxzyxFzyzyxFdSFxx),,(),,(前

矢量场散度的推导过程矢量场的散度是一个表示矢量场在给定点的发散程度的物理量。

它在流体力学、电磁学等领域具有重要的应用。

本文将详细介绍矢量场散度的推导过程，以帮助读者更好地理解。

首先，让我们从二维矢量场开始推导。

假设有一个二维平面，上面存在一个矢量场。

我们可以将该矢量场表示为一个二维向量函数V(x, y) = Vx(x, y) i + Vy(x, y) j，其中Vx和Vy是矢量场在x和y方向上的分量。

现在，我们想知道矢量场在给定点的发散程度。

我们可以通过比较给定点附近的两个小矩形区域的质量流量来推导散度。

假设我们选取一个小矩形区域，其边界长度为∆x和∆y，面积为∆A = ∆x∆y。

矢量场穿过该矩形区域的质量流量可以表示为Φ = Vx∆y - Vy∆x。

接下来，我们将对矢量场的散度进行定义。

假设我们选择该点附近的另一个小矩形区域，其边界长度为(∆x + ∆x')和(∆y + ∆y')，面积为∆A' = (∆x + ∆x')(∆y + ∆y')。

同样地，该矩形区域内的质量流量为Φ' = Vx(∆y + ∆y') - Vy(∆x + ∆x')。

现在，我们可以计算质量流量的变化量ΔΦ = Φ' - Φ。

展开上述表达式，我们可以得到ΔΦ = Vx∆y' - Vy∆x'。

通过将ΔΦ除以∆A'，我们可以得到单位面积上的质量流量变化量：ΔΦ/∆A' = (Vx∆y' - Vy∆x')/∆A'接下来，我们利用泰勒展开的思想，将∆y'和∆x'展开到一阶项，即∆y' ≈ ∂yVx∆x'，∆x' ≈ ∂xVy∆y'。

代入上述表达式，我们得到：ΔΦ/∆A' ≈ (Vx∂yVx - Vy∂xVy)∆x'∆y'/∆A'由于∆A' = (∆x + ∆x')(∆y + ∆y') ≈ ∆x∆y + ∂yVx∆x∆y +∂xVy∆x∆y，我们可以将上述表达式进一步简化为：ΔΦ/∆A' ≈ (Vx∂yVx - Vy∂xVy)∆A/∆A' ≈ (Vx∂yVx -Vy∂xVy)∆A/(∆x∆y + ∂yVx∆x∆y + ∂xVy∆x∆y)在极限∆x和∆y趋近于零的情况下，我们可以将上述表达式进一步简化为：ΔΦ/∆A' ≈ (Vx∂yVx - Vy∂xVy)/∂x(∂yVx - ∂xVy)继续化简上述表达式，我们可以得到：ΔΦ/∆A' ≈ (Vx∂yVx - Vy∂xVy)/(∂xVy - ∂yVx)最后，让我们将∆Φ/∆A'取极限。

1.3.3 散度定理（高斯定理）
表达式：
SA d S V A d V
式中S为V的外表面。 物理含义：
矢量A穿过任一封闭曲面S的总通量等于矢量散度在S 所包围体积V内的体积分。
散度定理的证明：
d iv A l V im 0 1 VS A d S d i v A V l i mA d S
【解】若使A成为一个无源场，即要求 A0
Aaz2xb2xy12zcx2xy (a2)z(2c)xb1 0 解得 a2,b1,c2
A ( 2 x z x 2 ) e x ( x y 2 y ) e y ( z z 2 2 x z 2 x y z ) e z
面，则：
内容小结 掌握通量、散度的物理意义
z h 围成的封闭曲面，求矢径r穿出S的柱面部分的通量。
【解】设s1和s2为闭合曲面S的顶部和底部的圆
z
面，则：
r ds r ds r ds
s
s1
s2
s1
rdv
v
s1 (xex yey zez ) (dydzex dxdzey dxdyez )
s2 (xex yey zez ) (dydzex dxdzey dxdyez )
通量指通过该曲面的矢线量，它代表曲面S内存在的通量源。
（3）在矢量场中，若
，称之为有源场， 称为(通量)源密度；
说明流出闭合面的通量小于流入曲面的通量，即闭合面内存在负源（沟）。
矢量场的通量-------通量源
矢量场的通量
1.矢量场的通量-------通量源 （2）散度代表矢量场的通量源的分布特性。
h
3 dv zdxdy zdxdy
v
s1
s2
3πa2h hdxdy 0dxdy

又：
dS nods ds cos(n, x)i ds cos(n, y) j ds cos(n, z)k dydzi dxdzj dydzk,
则通量可写成：
A dS Pdydz Qdxdz Rdxdy
s
s
例1：设由矢径 r xi yj zk 构成的矢量场中，
有一由圆锥面 x2 y2 z2 及平面 z H(H 0) 所围 成的封闭曲面S,如图，试求矢量场 从S内穿出S的
（2）简单曲面：
设连续曲面参数方程为：
x (u,v), y (u,v), z (u,v)
曲面上的每一点都只对应唯一的一个参数值（u, v）.(闭合
曲面闭合点除外)。简单曲面的一般特征是一条没有重点的连续 曲面。
1.通量
引例：
设有流速场v(M),流体是不可压缩的，设其密度为1.求单 位时间内流体向正侧穿过有向曲面S的流量Q（如图）。
取微元ds(微元内速度矢量和法矢 量近似看做不变)，则穿过ds的流量 dQ近似等于：
dQ vnds
以 n0 表示点M处的单位法矢量则
流量表示为：
dQ vnds (v n0 )ds v (n0ds)
令 dS n0ds, dS 为在点M处的这样一个矢量，其
方向与法向量n一致，其模等于面积ds。 据此，在单位时间内向正侧穿过S的流量，就
可用曲面积分表示为：
Q vnds v dS
s
s
又如：在电位移矢量D分布的电场中，穿过曲面S的
电通量：
e Dnds D dS
s
s
在磁感应强度矢量B分布的电场中，穿过曲面S的
磁通量： m Bnds D dS
s
s
通量定义：
设有矢量场A(M),沿其中有向曲面S某一侧的曲

实验证实麦氏方程组—电磁波的存在 近代俄国的波波夫和意大利的马可尼—电磁波传消息 无线电 当今电信时代——“电”、“光”通信
电磁应用
γ射线
医疗上用γ射线作为“手术刀”来切除肿瘤
x 射线
医疗、飞机安检，X射线用于透视检查
紫外线
医学杀菌、防伪技术、日光灯
可见光
七色光(红、橙、黄、绿、青、蓝、紫 ）
s r•d S v •Α d V v d V 3 • R 3
1.3.2矢量场的环量及旋度 1、环量的定义
设有矢量场A，l为场中的一条封闭的有向曲线， 定义矢量场A环绕闭合路径l的线 积分为该矢量的 环量，记作
l A dll A cosdl
矢量的环量和矢量穿过闭合面的通量一样，都是 描绘矢量场A性质的重要物理量，同样都是积分 量。为了知道场中每个点上旋涡源的性质，引入 矢量场旋度的概念。
红外线
在特定的红外敏感胶片上能形成热成像（热感应）
微波
军事雷达、导航、电子对抗 微波炉
无线电波
通信、遥感技术
本章主要内容
1、矢量及其代数运算 2、圆柱坐标系和球坐标系 3、矢量场 4、标量场 5、亥姆霍兹定理
1.1矢量及其代数运算
1.1.1标量和矢量
电磁场中遇到的绝大多数物理量， 能够容易地区分为 标量（Scalar）和矢量(Vector)。 一个仅用大小就能够 完整描述的物理量称为标量， 例如， 电压、温度、 时间、质量、电荷等。 实际上， 所有实数都是标量。 一个有大小和方向的物理量称为矢量， 电场、磁场、 力、速度、力矩等都是矢量。例如， 矢量A可以表示 成
《矢量分析与场论》PPT 课件
课程体系
电磁理论
电磁基本理论
电磁工程
产生、辐射、

⎝
2⎠
⎝
2⎠
Ay
⎜⎛ x,y+Δy,z ⎟⎞ ⎝ 2⎠
=
Ay
(x,y,z)
+
∂Ay ∂y
(x,y,z)
Δy 2
+
1 2!
∂2 Ay ∂y2
( Δy )2 2
+ ...
得
ΔΨr
=
( Ay
+
∂Ay ∂y
Δy 2
+ .........) ΔxΔz
divA 直角坐标表示式的推导
11
§1.2通量、散度、散度定理
8
§1.2通量、散度、散度定理
作业：1.1-1,1.1-3,1.1-5
S为封闭面时： 若Ψ > 0， 有净通量流出，说明S内有源； 若Ψ < 0， 有净通量流入，说明S内有洞(负源); 若Ψ = 0， 则净通量为零，说明S内无源。
举例：
由《大学物理》知，电通量 Ψe = ∫sD ⋅ ds = Q（高斯定理） 水流的单位时间流量（米3/秒）＝ v ⋅ d s
A 矢量的模：
γ
β o
Ay
α Ax
y
A = A = Ax2 + Ay 2 + Az 2
x
A 的单位矢量：
Aˆ = A = xˆ Ax + yˆ A y + zˆ Az AA AA
= xˆ cosα + yˆ cos β + zˆ cosγ
2
§1.1矢量代数
二、标量积和矢量积
a) 标量积（点乘）
加减乘除
∂y 4π r 5
∂Dz = q r 2 − 3z 2
∂z 4π r 5

天津大学电子信息工程学院二零一四年目录一、标量场和矢量场 (1)二、矢量的通量散度 (6)三、矢量的环流旋度 (9)四、标量场的梯度 (12)五、亥姆霍兹定理 (15)小结 (16)习题 (18)附录1 电磁场与电磁波主要物理量符号和单位 (20)附录2 重要的矢量公式 (24)一、标量场和矢量场物理量场的概念是指，在空间区域的每一点，都有该物理量确定的值与之对应。

即物理量数值的无穷集合表示一种场。

如果此物理量为标量（一个仅用数值就可以表示的物理量，如温度），这种场就称为标量场，如温度场、密度场、电位场等。

如果此物理量为矢量（需要用数值及方向表示的物理量，如速度），这种场就称为矢量场，如速度场、力场、电磁场等。

仅与空间有关的场，称为静态场；与空间、时间都相关的场，称为动态场。

矢量：可以用一段有向线段来表示，如图1-1所示，记为A ，A 为A 的模。

线段长度表示模的大小，箭头是A 的方向。

单位矢量：用来表示矢量的方向 ，记为A ，其模为1，即：//A A A A A ==A AA = （1-1）三种常用的坐标系：()()(),,,,,,x y zz ϕϕθϕθϕ⎧ ⎪⎪⎨⎪⎪ ⎩直角坐标系 x,y,z; 正交坐标系圆柱坐标系r,,z;r 球坐标系r,,;rA图1-1 矢量表示圆柱坐标系、球坐标系对应的自变量与三个矢量方向关系，分别如图1-2、图1-3所示。

图1-2 圆柱坐标系参量示意图图1-3 球坐标系参量示意图位置矢量：从坐标原点指向空间位置点的矢量，记为r 。

对直角坐标系有r xx yy zz =++。

r 与空间位置点(),,x y z 有着一一对应的关系，即空间位置点(),,x y z 可以用位置矢量r 表示。

三维空间的矢量场可以分解为三个分量场， ()()()()x y z F r x F r y F r z F r = + + 。

其中()()()x y z F r F r F r 、、为标量场。

直角坐标系中散度的计算公式在数学和物理学中，散度（Divergence）是一个向量场的一个重要概念。

它描述了向量场在某一点的流出和流入程度，通常表示为div(F)或∇·F。

在直角坐标系中，散度的计算公式可以用来计算任意向量场的散度。

散度的定义散度是矢量场的一种性质，它描述了矢量场的变化率。

在直角坐标系中，一个三维向量场可以表示为F = (P, Q, R)，其中P、Q、R分别表示在x、y、z方向上的分量。

散度可以通过对向量场的每个分量取偏导数并相加来计算。

在直角坐标系中，一个三维向量场F的散度定义为：div(F) = ∂P/∂x + ∂Q/∂y + ∂R/∂z其中，∂P/∂x、∂Q/∂y和∂R/∂z分别表示F在x、y、z方向上的偏导数。

散度的物理意义散度描述了向量场的流入和流出程度，可以用于描述物质的扩散和集聚的情况。

如果散度为正值，表示向量场在某一点的流出较多；如果散度为负值，表示向量场在某一点的流入较多；如果散度为零，表示向量场在某一点无流入流出。

在物理学中，散度也常被用于描述电场和磁场等物理量的分布情况。

当散度不为零时，代表该物理量在某一点有源或涡旋；当散度为零时，代表该物理量在某一点无源无涡旋。

示例计算接下来，我们将以一个简单的例子来计算直角坐标系中一个二维向量场的散度。

考虑一个二维向量场F = (2x, -3y)，我们希望计算该向量场在每个点的散度。

根据散度的计算公式，我们需要计算分别对x和y的偏导数。

对于这个二维向量场，我们有：F = (2x, -3y)分别对x和y求偏导数，可以得到：∂F/∂x = 2, ∂F/∂y = -3将上述结果代入散度的计算公式，可得：div(F) = ∂(2x)/∂x + ∂(-3y)/∂y = 2 - 3 = -1因此，该向量场在每个点上的散度为-1。

结论本文介绍了直角坐标系中散度的计算公式，并且给出了一个示例计算。

散度是矢量场的一种属性，描述了向量场在某一点的流出和流入程度。

div A = A
可以证明, 散度运算符合下列规则:
(A ± B ) = A ± B (φ A ) = φ A ± A φ
20
1.2通量 散度、 通量、 §1.2通量、散度、散度定理
三、高斯散度定理
矢量场的散度代表其通量的体密度,因此散度的体积分 等于穿过包围该体积封闭面的总通量:
（1）开曲面：沿封闭曲线 n的取法：
l 的绕行方向按右手螺旋的拇指方向
（2）封闭面： 取为封闭面的外法线方向 外法线方向
14
矢量A穿过整个曲面S的通量:
Φ = ∫ A ds = ∫ A nds
s s
如果S是一个封闭面, 则
Φ = ∫ A ds
S
15
1.2通量 散度、 通量、 §1.2通量、散度、散度定理
22
1.2通量 散度、 通量、 §1.2通量、散度、散度定理
同理
D y
q r 2 3y 2 = y 4π r5
D z q r 2 3z 2 = z 4π r5
故
Dx D y Dz q 3r 2 3( x 2 + y 2 + z 2 ) D = + + = =0 5 x y z 4π r
可见，除了点电荷所在源点 (r = 0)外，空间各点的电通密度散度均为 ，它是管形场 。 空间各点的电通密度散度均为0， 可见，
（C点）
电偶极子的电力线和等位线 17
1.2通量 散度、 通量、 §1.2通量、散度、散度定理
b) 散度的分量表示式
穿过包围点P(x,y,z)的无穷小体积 v = xyz 的通量： 的通量： 计算 A 穿过包围点 的无穷小体积 右边向外流出的通量： A 穿过右边 右边

2 x 2 y 2 z 2
二、矢量积 Cross production 定义：矢量积A×B是一个矢量, 其大小等于两个矢量的模
值相乘, 再乘以它们夹角αAB(≤π)的正弦, 其方向与A , B成右手螺
旋关系, 为 ˆ A , B所在平面的右手法向 n :
ˆ A B sin aAB A B n
第一章 矢 量 分 析
Chapter 1 Vector Analysis §1.1 矢量表示法和运算 §1.2 通量与散度,散度定理
§1.3 环量与旋度,斯托克斯定理
§1.4 方向导数与梯度,格林定理 §1.5 曲面坐标系 §1.6 亥姆霍兹定理
基本要求
1. 掌握矢量在正交坐标系中的表示方法 2. 掌握矢量的代数运算及其在坐标系中的物理意义 3. 掌握矢量积、标量积的计算 4. 了解矢量场散度的定义，掌握其计算方法和物理意义；掌 握散度定理的内容，并能熟练运用。
1 .3 .1 环量 Curl of a vector field
矢量A沿某封闭曲线的线 积分, 定义为A沿该曲线的环 量(或旋涡量), 记为


l
A dl
1 .3 .2 旋度的定义和运算
1、定义：
为反映给定点附近的环量情况, 我们把封闭曲线收小, 使它包围的 面积ΔS趋近于零, 取极限 A dl l lim S 0 S
物理量的表示 • 矢量：大写黑体斜体字母
A 大写斜体字母加表示矢量的符号 A
• 标量：小写斜体字母 u ˆ x • 单位矢量：小写上加倒勾
ex
ex
§1 .1 矢量表示法及其运算
1 .1 .1 矢量表示法及其和差
若一个矢量在三个相互垂 直的坐标轴上的分量已知 , 这 个矢量就确定了。 例如在直角

(r), a(r)
1.1 标量、矢量、场
场的几何表示
标量场可用函数等值面（线）来表示。 可直观看出函数值的大小分布，以及变 化快慢
矢量场可用矢量线来表示。 任一点的矢量方向可由矢量线的切线方 向定出；也可以从矢量线的疏密程度估 计矢量在各点的大小。
1.2 标量场的梯度
方向导数（Directional Gradient）
1. 如果一个方程式或表达式的一项中，一种下标只出现一次，则 称之为自由指标，自由指标在表达式或方程的每一项中必须只 出现一次。 2. 如果在一个表达式或方程的一项中，一种指标正好出现两次， 则称之为哑指标，它表示从1到3求和。哑指标在其他任何项中 可以刚好出现两次，也可以不出现。 3. 如果在一个表达式或方程中的一项中，一种指标出现的次数多 于两次，则是错误的。
2 3
2
ij ij ij ij
i 1 j 1
3
3
1111 1212 1313 21 21 22 22 23 23 31 31 32 32 33 33
1.4 张量表示法
自由指标： 定义：凡在同一项内不重复出现的指标。如
i j k x y z
是一个矢性微分算子，即在运算中具有矢量和微分的双重性质， 其运算规则是：
u u u u i j k x y z
Ay Ax A A i j z k x y z
Az Ay Ax Az Ay Ax A y z i z x j x y k
2 ( ) ( ),ij xi x j
uk ,ij
2uk xi x j
1.5 坐标变换与张量定义

左 A d S ＋ 右 A d S ＝ 左 A （ a y ) dy x 0 ＋ 右 d A a y d zy x 1 ＝ 0 d 1 2 1 2 z
上 A d S ＋ 下 A d S ＝ 上 A a z dz x 1 ＋ 下 d A ( a z y ) dz x 0 ＝ 1 2 d 0 1 2 y
rX ax Y ayZ az (1 1 2 )
即空间中点P(X,Y,Z)能够由它在三个相互垂直的轴线上的投 影唯一地被确定。
4. 直角坐标系中，矢量 A 可以表示为
AAxaxAyayAzaz
A Ax2Ay2Az2
1.1.2 矢量的代数运算 设两个矢量为 A e x A x e y A y e z A z ，B e x B x e y B y e z B z ，则
1.标量积(Scalar Product) ：
A B AcB o s A xB xA yB yA zB z －－－－标量
标量积服从交换律和分配律，即
A B B A ,A (B C ) A B A C
2.矢量积(Vector Product) ：又称矢量的叉积(Cross Product)。
exeyeyez exez 0
exexeyeyezez 1
e x ey e z,ey e z e x,e z e x ey
exexeyeyezez0
1.3 矢量场
本节要点：－－考察矢量场在空间的分布及变化规律。 矢量线 通量和散度 环量与旋度
divA 0，表明 A 在该点有散发通量之正源，称为源点； divA 0，表明 A 在该点有吸收通量之负源，称为汇点； divA 0，表明 A 在该点无通量源，称为连续或无散的。

S V
高斯定理
散度定理 The divergence theorem
散度定理：
既然矢量的散度代表的通过一个点流出或流入量的大小, 因此矢量场散度的体积分等于该矢量穿过包围该体积的封 闭面的总通量, 即
V 上式称为散度定理, 也称为高斯定理。

Adv A ds
场物质的守恒定律
高斯定理的物理意义： 从数学角度可以认为高斯定理建立了面积分和体积分的关系。 从物理角度可以理解为高斯定理建立了区域 V 中的场和包围区域 V 的闭合面 S 上 的场之间的关系。 如果已知区域 V 中的场，根据高斯定理即可求出边界 S 上的场，反之亦然。

L
A dl
ΔS0
ΔS
这个极限的意义就是在一个点上的环流的面密度, 或称环量强度。Curl(A)叫做旋度。任 意方向的曲面的环流强度是旋度在这个方向上面的投影。 旋度的物理意义
1) 矢量A的旋度是一个矢量, 其大小是矢量A在给定点处的最大环量面密度, 其方向就是当面元的取向使环量
面密度最大时, 该面元矢量的方向 2) 3) 它描述A在该点处的旋涡源强度。 若某区域中各点curl A=0, 称A为无旋场或保守场。 。
Ax dx Ay dy Az dz
L
A dl
L
0 0 0
越大/越小, 说明什么？
旋度的定义和运算
1、定义： 为反映给定点附近的环量情况, 我们把封闭曲线收小, 使它包围的面积ΔS 趋近于零, 取极限
ˆ lim curl(A) n
固定 R 时, 沿着梯度方向移动 T 变化最大.
多元函数的梯度:
T ( x) T e1 x
T ( x, y ) T T e1 e2 x y