§1.3 矢量场的通量及散度
- 格式:pps
- 大小:330.00 KB
- 文档页数:12




散度通量散度和通量都是物理学中涉及到矢量场的概念。
在理解散度和通量之前,需要先了解矢量场的概念。
矢量场是指在空间中各点都有一个矢量与之对应的场。
“矢量”是指具有大小和方向的物理量,比如速度、力等。
在三维空间中,矢量通常用箭头表示,箭头长度代表矢量的大小,箭头指向代表矢量的方向。
矢量场描述了在空间中每个点的矢量是什么。
散度是描述矢量场的一个物理量。
它表示在一个给定点上的矢量场流出或流入的程度。
可以理解为矢量场的源与汇。
如果在一个点上,矢量场大量流出,则散度为正;如果流入,则散度为负;如果没有流入或流出,则散度为零。
通量则是散度的一种数学描述。
通量表示的是矢量场通过一个给定平面的流量,也可以理解为矢量场与该平面垂直的分量。
通量可以用来衡量矢量场在某个平面上的流动情况。
为了更好地理解散度和通量的概念,可以通过一个具体的例子来说明。
假设有一个假想的空气流场,我们在其中放置了一个球体。
球体内外的空气流动方式可能会有所不同。
在球体表面上,空气可能会流出或者流入。
如果空气大量流出,那么球体内的分子数就会减少,表示散度为正。
反之,如果空气流入球体内,散度就为负。
如果球体内外的空气流动情况相同,则表示散度为零。
与散度不同,通量主要描述的是矢量场通过某个平面的情况。
假设我们取球体表面为一个平面,那么空气流动通过这个平面的通量就是描述空气流动情况的一个量。
如果通量为正,表示有空气流出;如果通量为负,表示有空气流入;如果通量为零,则表示球体内外的空气流动情况相同。
散度和通量是紧密相关的物理量,它们描述了矢量场在空间中的流动情况。
散度描述了在一个给定点上的流出或流入程度,而通量描述了通过某个平面的流动情况。
需要注意的是,散度和通量是不同的概念。
散度是一个矢量场的性质,它是矢量场的一个标量函数;而通量是矢量场与一个平面垂直分量的大小。
在数学上,散度通过向量微积分中的散度算子表示,通量则是矢量场在某个平面上的贡献。
总结起来,散度和通量都是矢量场中重要的物理概念。






通量和散度的概念通量和散度是物理学中用来描述流过某一表面的物理量的概念。
它们在物理学的各个领域都有着广泛的应用,包括电磁学、流体力学和热力学等。
下面我将详细介绍这两个概念及其相关的理论和应用。
通量是一个贯穿某一表面的物理量的总量。
在物理学中,通量的概念经常用来描述一些物理量在一定时间内通过某一固定面积的流量。
通量可以是质量、能量、电荷等物理量的流量。
它的计算公式为:通量= 流量/ 时间。
通量的单位取决于所描述的物理量,例如,若是质量的通量,则单位为千克/秒;若是能量的通量,则单位为焦耳/秒。
散度是矢量场的一种性质,用来描述线、面、体积上物理量的变化情况。
矢量场是一个在空间中定义了每一个点上值与方向的矢量的场。
散度描述了一个矢量场的源头或汇聚情况,即在某一点上是否有物理量流入或流出这一点。
它的计算公式为:散度=(偏导数x方向上的分量+ 偏导数y方向上的分量+ 偏导数z方向上的分量)。
散度是一种标量场,它的大小和分布描述了物理量的变化情况,正负号则表示物理量流的方向。
如果散度为正,则表示物理量从该点流出;如果散度为负,则表示物理量流入该点;如果散度为零,则表示物理量在该点不变。
通量和散度之间有一个重要的关系,即散度定理。
散度定理是高斯定理的一种特殊形式,它表明通过一个闭合曲面的通量等于该曲面内散度的体积分。
通俗地讲,散度定理说明了通过一个封闭的表面的物理量总量等于该表面内物理量的来源或消耗总量。
散度定理为物理学家提供了一个非常有用的工具,可以利用这个定理来简化复杂的物理问题的计算。
通量和散度在电磁学中具有重要的应用。
在电磁学中,电场和磁场都可以用矢量场的形式来描述。
通量定律和散度定理是电磁场中的两个基本定律。
例如,根据电场的散度定理,通过一个封闭曲面的电场通量等于该曲面内电荷的总量除以真空介电常数。
这个定理为计算电场的分布和与电荷相互作用提供了一种简洁而有效的方法。
类似地,磁场的散度定理也可以用于计算磁场的分布以及与电流的相互作用。
高数之高斯公式通量与散度高斯公式,也称为高斯定理或高斯‐斯托克斯定理,是矢量分析中的一个重要定理,用于计算矢量场的通量与散度之间的关系。
它是高等数学课程中的一个重要知识点,也是理解物理学、电磁学等领域中的许多现象的基础。
首先,让我们先来了解一下通量和散度的概念。
通量可以理解为矢量场通过一些封闭曲面的流量,即场的一些属性通过单位面积的流量。
通量的计算可以用于解释许多自然现象,比如液体或气体的流动、电场的分布等等。
散度则是矢量场在其中一点上的变化率,表示场在该点的流入流出程度。
散度可以用于描述场的源和汇。
高斯公式则是描述通量和散度之间关系的数学公式,它的数学表达如下:∬S F·dS = ∭V(nabla·F)dV其中,∬S表示对曲面S的积分,F表示矢量场,dS表示曲面S上的面积元素,∭V表示对体积V的积分,nabla·F表示矢量场F的散度。
从公式中可以看出,高斯公式表示了一个重要的等式:其中一矢量场通过其中一封闭曲面的通量等于该场在该曲面所包围的体积中的散度的积分。
也就是说,一个矢量场通过一个封闭曲面的总流量与该场在该曲面所包围的体积中的散度的总和是相等的。
这个公式的物理意义非常重要。
比如,在电磁学中,我们可以将电场看作矢量场,通过高斯公式可以得到一个非常重要的结论:电场通过一个封闭曲面的总通量等于该曲面所包围的电荷的总电荷量的1/ε0倍,其中ε0为真空中的电介质常数。
这就是著名的高斯定律,它是电磁学的基础之一高斯公式也可以应用于流体力学中,用于计算液体或气体通过其中一曲面的流量。
在这种情况下,矢量场就是流速场,而散度就是流速场的变化率,可以描述液体或气体在其中一点上的流入流出程度。
总结起来,高斯公式是描述通量和散度之间关系的重要工具,适用于解释许多自然现象,包括电磁学、流体力学等多个领域。
通过应用高斯公式,我们可以定量地描述和计算矢量场的通量和散度之间的关系,从而更好地理解和解释现象。
1.3矢量场的通量及散度1.3.1矢量场的概念定义:空间区域V 内的某一物理系统的状态,可以用一个矢量函数F (r ,t )来描述。
对于V 中任意一点r ,若F (r ,t )有确定的值与之对应,则称F (r ,t )是定义于V 区域上的矢量场。
矢量场也有两个特点:①F (r ,t )为空间坐标的函数(点函数),显示单值性;②F (r ,t )要占有一个空间。
矢量场也分恒稳矢量场F (r )和时变矢量场F (r , t )。
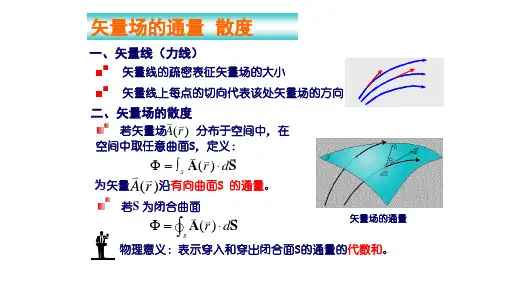
矢量场F (r ,t )可用矢量线(简称F 线)来形象地描述。
F 线是带有箭头的空间曲线,其上任一点的切线方向即为该处矢量场的方向,F 线的疏密反映矢量场分布的弱或强,矢量线互不相交。
直角坐标系下矢量场可表为:()()()()z z y y x x z y x F z y x F z y x F z y x e ,,e ,,e ,,,,F ++=(1.3.1)F 线上的任一线元矢量d l 总是与该处的F 共线,有 即则F 线的微分方程zy x F zF y F x d d d == (1.3.2) 1.3.2. 矢量场的通量(1)恒稳液流场v (r )液体流动形成液流场,其中每一点的流动特点用流速v (r )表示,反映单位时间内流过与该处液流方向垂直的单位面积的液体体积的多少。
恒稳之意是指与时间无关恒稳液流场⇔恒稳流速矢量场v (r )。
2)流量概念面元矢量:对于S 面上的任意面元d S ,指定其正法向方向,设置正法向单位矢量e n ,确定了正法向方向的面元称为面元矢量,表示为d S =d S e n 。
流量:设面元矢量d S 与该处v 间的夹角为θ,则穿过该面元d S 的元流量为ψd = v n d S = v cos θd S = v ‧d S (1.3.3)累加S 面上所有面元的元流量,得穿过S 面的流量⎰⎰⋅==sS v d d ψψ(1.3.4)推广流量的概念,对于任意闭合面,有v (r )在闭面S 上的闭合面积分⎰⋅=s d s v ψ(1.3.5)规定闭面上各d S 的方向为外法线方向,上式就表示流出闭面S 的净流量。
§1.3 矢量场的通量及散度
1、矢量场定义及图示
对于空间区域V 内的任意一点r ,若有一个矢量F (r )与之对应,我们就称这个矢量函数F (r )是定义于V 的矢量场。
恒稳矢量场F (r ) ,时变矢量场F (r ,t )。
矢量场图--矢量线0
l F =⨯d 其方程为
矢量线的示意图
F 线
F
d l
矢量线
F (x,y,z )=F x (x,y,z ) e x +F y (x,y,z )e y +F z (x,y,z )e z
(F y d z -F z d y )e x +(F z d x -F x d z )e y +(F x d y -F y d x )e z =0F y d z -F z d y =0F z d x -F x d z =0
F x d y -F y d x =0
或
得直角坐标式的矢量线方程
z
y x F z F y F x d d d ==矢量场的直角坐标式为
l F =⨯d
矢量F 沿有向曲面S 的面积分
S
F d ⋅⎰=S Ψ2、通量
矢量F 在面元d S 的面积分为d ψ= F n d s =F cos θd S =F ‧d S 矢量场的通量
若S为闭合曲面,可以根据净通量的大小判断闭合面中源的性质:
⎰⋅
=
s
Ψs
F d
ψ> 0(有正源)
ψ< 0(有负源)ψ= 0(无源)
矢量场的闭合面通量
在直角坐标系中,设
F (x,y,z ) =F x (x,y,z )e x + F y (x,y,z )e y + F z (x,y,z )e z d s =d y d z e x + d x d z e y + d x d y e z
则通量可写成
⎰
⎰++=⋅=s
z y x s
y
x F z x F z y F Ψd d d d d d d s F
如果包围点P 的闭合面∆S 所围区域∆V 以任意方式缩小为点P 时, 通量与体积之比的极限存在,我们就将它定义为P 点处F (r )
的散度(divergence ),记作
V
s V ∆⋅⎰→∆s F lim d 03 散度
V
div s
V ∆⋅=
⎰→∆s F F d lim
z
z z z y
y y y x
x x x z z
x,y,z F x,y,z F z x,y,z y y x,y,z F x,y,z F y,z x,y x x x,y,z F x,y,z F x,y,z x e F e F e F ])
()([)(])
()([)(])
()([)Δ(∆∂∂+≈∆+∆∂∂+≈∆+∆∂∂+≈+求边长分别为∆x 、∆y 、∆z 的小平行六面体的通量,其体积∆V =∆x ∆y ∆z 。
根据泰勒极数可知
a c
b
F x (x+∆x,y,z )
F y (x,y+∆y,z )
F z (x,y,z+∆z )x
y
z
o
∆x
∆y
∆z (x,y,z )F x (x,y,z )
F y (x,y,z )
F z (x,y,z )
直角坐标的微分体积
V z
F y F x F y x F y x z z F F z x F z x y y F F z y F z y x x F F z y x z z
z y y y x x
x ∆∂∂+∂∂+∂∂=∆∆-∆∆∆∂∂++∆∆-∆∆∆∂∂++∆∆-∆∆∆∂∂+⋅≈⎰
)()]
)[()]
)[()])[(d s
s F z
F y F x F V
div z
y x s
V ∂∂+∂∂+∂∂=∆⋅=
⎰→∆s F F d lim
z
F y F x F z
y x ∂∂+
∂∂+∂∂=⋅∇F 或写成
即得
a c
b
F x (x+∆x,y,z )
F y (x,y+∆y,z )
F z (x,y,z+∆z )x
y
z
o
∆x ∆y
∆z (x,y,z )F x (x,y,z )
F y (x,y,z )
F z (x,y,z )
直角坐标的微分体积
4、散度的物理意义
•
散度代表矢量场的通量源的分布特性∇• F= 0(无源
)
∇• F= -ρ<0(负源
)
∇• F= ρ>0(正源)•矢量的散度是一个标量,是空间坐标点的函数;
5、散度运算的几个基本关系式
•相对坐标矢量函数)
(r r F '-F
F ⋅∇'-=⋅∇)
(r r R '-•相对位置矢量
3
=⋅∇R •标量场 f (r ) 和矢量场F (r ) 之积f F
F
F F ⋅∇+⋅∇=⋅∇f f f )(•R 及其模R
03=⋅∇R
R 0
≠R
F
F F ⋅∇+⋅∇=⋅∇f f f )(证明:设
f (r )=f (x ,y ,z ),
F (x,y,z )=F x (x,y,z )e x + F y (x,y,z )e y + F z (x,y,z )e z
则
)
()()(z z y y x x z y x fF fF fF z y x f e e e e e e F ++⋅∂∂
+∂∂+∂∂=⋅∇)()()(z y x F f z
F f y F f x ∂∂
+∂∂+∂∂=)
()()(z f
F z F f y f F y F f x f F x F f z z y y x x ∂∂+∂∂+∂∂+∂∂+∂∂+∂∂=)
()(z
f F y f F x f F z F y F x F f z y x z y x ∂∂+∂∂+∂∂+∂∂+∂∂+∂∂=F
F ⋅∇+⋅∇=f f
03=⋅∇R
R R
F =3
1R f =
证明:设:
f
f f ∇⋅+⋅∇=⋅∇F F F )(3311R
R ∇⋅+⋅∇=R R R R R ∇'
⎪⎭
⎫ ⎝⎛⋅+=3313R 03343=⎪⎭⎫ ⎝⎛-⋅+=R
R R R R
x y a
z b S 1
o
S 5S 4S 3S 2
例3
已知F (x,y,z ) =yz e x +xz e y +xyz e z ,试求它穿过闭合面的部
分圆柱面S 1的通量。
x = a cos α,y =a sin α
S 1上的F 写成F =az sin αe x + az cos αe y + a 2z sin αcos α
e z
因d s 1=a d αd z e n
则
F ‧d s 1=[a 2z sin α(e x ‧e n )+a 2z cos α(e y ‧e n )
+ a 3z sin αcos α(e z ‧e n )]d αd z =2a 2z sin αcos αd αd z
2
sin 2
d cos sin )]d d 2(cos sin [d 2
2/2
/2
22
22
2b
2
/2
11
b a b
a b
a z z a s =
===⋅⎰
⎰⎰⎰
πππα
αααα
ααs F 所以
解
在S 1面上有圆的参数方程:
d α
d z
αx
y e n d s
z
b
S 1a d αo π/2S 5
S 4
S 3
S 2。