平面曲线的弧长

第十章 定积分的应用 3 平面曲线的弧长与曲率一、平面曲线的弧长设平面曲线C=⌒AB. 如图所示，在C 上从A 到B 依次取分点： A=P 0,P 1,P 2,…,P n-1,P n =B ，它们成为曲线C 的一个分割，记为T. 用线段联结T 中每相邻两点，得到C 的n 条弦P i-1P i (i=1,2,…,n)，这n 条弦又成为C 的一条内接折线，记：T =ni 1max ≤≤|P i-1P i |，s T =∑=n1i i 1-i |P P |，分别表示最长弦的长度和折线的总长度。

定义1：对于曲线C 的无论怎样的分割T ， 如果存在有限极限：0T lim →s T =s ，则称曲线C 是可求长的， 并把极限s 定义为曲线C 的弧长.定义2：设平面曲线C 由参数方程x=x(t), y=y(t), t ∈[α,β]给出. 如果x(t)与y(t)在[α,β]上连续可微，且x ’(t)与y ’(t)不同时为零 (即x ’2(t)+y ’2(t)≠0, t ∈[α,β])，则称C 为一条光滑曲线.定理：设曲线C 由参数方程x=x(t), y=y(t), t ∈[α,β]给出. 若C 为一光滑曲线，则C 是可求长的，且弧长为：s=⎰'+'βα22(t)y (t)x dt.证：对C 作任意分割T={P 0,P 1,…,P n }，并设P 0与P n 分别对应t=α与t=β, 且P i (x i ,y i )=(x(t i ),y(t i )), i=1,2,…,n-1.于是，与T 对应得到区间[α,β]的一个分割T ’： α=t 0< t 1<t 2<…t n-1<t n =β.在T ’所属的每个小区间△i =[t i-1,t i ]上，由微分中值定理得△x i =x(t i )-x(t i-1)=x ’(ξi )△t i , ξi ∈△i ；△y i =y(t i )-y(t i-1)=y ’(ηi )△t i , ηi ∈△i . 从而C 的内接折线总长为s T =∑=∆+∆n1i 2i 2i y x =∑='+'n1i i 2i 2)(ηy )(ξx △t i .记σi =)(ηy )(ξx i 2i 2'+'-)(ξy )(ξx i 2i 2'+'，则s T =[]∑=+'+'n1i i i 2i 2σ)(ηy )(ξx △t i .又由三角形不等式可得：|σi |≤||y ’(ηi )|-|y ’(ξi )||≤|y ’(ηi )-y ’(ξi )|. 由y ’(t)在[α,β]上连续，从而一致连续，∴对任给的ε>0, 存在δ>0， 当T '<δ时，只要ηi , ξi ∈△i ，就有|σi |≤|y ’(ηi )-y ’(ξi )|<α-βε, i=1,2,…,n. ∴|s T -∑='+'n1i i 2i 2)(ξy )(ξx △t i |=|∑=n1i i σ△t i |≤∑=n1i i |σ|△t i <ε,∴0T lim →s T =∑=→''+'n1i i 2i 20T )(ξy )(ξx lim △t i ，即s=⎰'+'βα22(t)y (t)x dt.注：1、若曲线C 由直线坐标方程y=f(x), x ∈[a,b]表示，则看作参数方程：x=x, y=f(x), x ∈[a,b]. 因此，当f(x)在[a,b]上连续可微时，此曲线即为一光滑曲线，其弧长公式为：s=⎰'+ba 2(x )f 1dx. 2、若曲线C 由极坐标方程r=r(θ), θ∈[α,β]表示，则 化为参数方程：x=r(θ)cos θ, y=r(θ)sin θ, θ∈[α,β]. 由x ’(θ)=r ’(θ)cos θ-r(θ)sin θ, y ’(θ)=r ’(θ)sin θ+r(θ)cos θ, 得：x ’2(θ)+y ’2(θ)=r 2(θ)+r ’2(θ)，∴当r ’(θ)在[α,β]连续，且r(θ)与r ’(θ)不同时为零时，此极坐标曲线为一光滑曲线， 其弧长公式为：s=⎰'+βα22 )(θr )(θr d θ.例1：求摆线x=a(t-sint), y=a(1-cost)(a>0)一拱的孤长.解：∵x’(t)=a-acost; y’(t)=asint. ∴x’2(t)+y’2(t)=2a2(1-cost)=4a2sin22t.其弧长为s=⎰2π222tsin4a dt=4a⎰2π02tsin d⎪⎭⎫⎝⎛2t=8a.例2：求悬链线y=2ee-xx+从x=0到x=a>0那一段的弧长.解：∵y’=2ee-xx-. ∴1+y’2=2x-x2ee⎪⎪⎭⎫⎝⎛+.其弧长为s=⎰+a-xx2ee dx=2ee-aa-.例3：求心形线r=a(1+cosθ) (a>0)的周长.解：∵r’(θ)=-asinθ. ∴r2(θ)+r’2(θ)=4a2cos22θ.其周长为s=⎰2π02θacos2dθ=4a⎰2π02θcos d⎪⎭⎫⎝⎛2θ=8a.注：∵s(t)=⎰'+'tα22(t)y(t)x dt连续，∴dtds=22dtdydtdx⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛，即有ds=22dydx+. 特别称s(t)的微分dx为弧微分. (如左下图)PR为曲线在点P处的切线，在Rt△PQR中，PQ为dx，QR为dy，PR则为dx，这个三角形称为微分三角形。

§3 平面曲线的弧长与曲率一 平面曲线的弧长先建立平面曲线弧长的概念，设C=AB 是一条没有自交点的非闭的平面曲线，在C 上从A 到B 依次取分点A=P 0,P 1,P 2,…，P n =B,它们成为对曲线C 的一个分割，记为T ，然后用线段连接T 中每相邻两点，得到C 的n 条弦1(1,2,...,)i i P P i n -=，这n 条弦又成为C 的一条内接折线，记||T||=max|P i-1P i |,11||nT i ii s PP -==∑分别表示最长弦的长度和折线的总长度。

定义1 如果存在有限极限||||0lim s T T s →=，即任给ε>0,恒存在δ>0，使得对于C 的任何分割T ，只要||T||<δ，就有|s T -s|<ε,曲线C 是可求长的，并把s 定义为曲线C 的弧长。

定理10.1 设曲线C 是一条没有自交点的非闭的平面曲线，由参数方程x=x(t),y=y(t),t ∈[α,β]给出，若x(t)、y(t)在[α,β]上连续可微，则C 是可求长的，且弧长为s βα=⎰。

证明 对C 作任一分割T={ P 0,P 1,P 2,…，P n },并设P0与Pn 分别对应t=α和t=β,且P i (x i ,y i )=(x(t i ),y(t i )),i=1,2,…,n -1,于是与T 对应得到区间[α,β]的一个分割T'：α=t 0,t 1,t 2,…,t n =β。

现在用反证法先证明||||0lim ||||0T T →'=.假设||||0lim ||||0T T →'≠，则存在ε0>0，对于任何δ>0，都可以找到一个分割T 使得||T||<δ而同时||T'||>ε0,从而可以找到C 上两点Q'和Q''，使得|Q''Q'|<δ，而它们对应的参量t'和t''满足|t't''|≥ε0,依次取δ=1/n,n=1,2,…,则得到两个点列{Q'n }和{Q''n }和它们对应的参量数列{t'n }和{t''n },它们满足|Q n ''Q n '|<1/n, |t'n t''n |≥ε0,由致密性定理，存在子列{}{}k kn n t t '''及,和t*和t**∈[α,β]，使得lim *,lim **k knn k k t t t t →∞→∞'''==，显然|t*-t**|≥ε0,即t*≠t**。

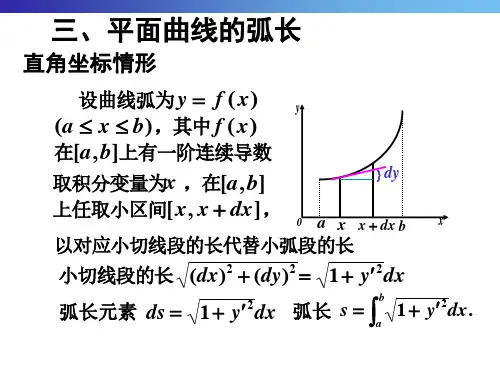
定积分计算弧长公式弧长公式是计算曲线弧长的一种工具，通过定积分来求解。

弧长公式在多个领域应用广泛，如物理、数学、工程等。

在本文中，我们将介绍弧长公式的推导过程，并给出一些常见曲线的弧长计算示例。

我们首先考虑平面上的一条曲线，可以表示为y=f(x)。

我们的目标是计算曲线一段区间[a,b]的弧长。

我们将区间[a,b]等分成n个小区间，每个小区间的长度为Δx=(b-a)/n。

在每个小区间上，我们可以通过线段的长度来近似曲线上的弧长。

设曲线上一点(x,f(x))，它与相邻点(x+Δx,f(x+Δx))之间的线段长度为s。

根据勾股定理，我们有：s=√((Δx)²+(Δy)²)其中Δy=f(x+Δx)-f(x)为两个点在y轴上的纵向距离。

为了得到曲线上所有小线段的长度之和，我们要对每个小区间[x_i,x_i+1]上的线段长度进行求和。

我们可以将弧长公式表示为一个求和的形式：S=∑s_i其中s_i为小区间[x_i,x_i+1]上的线段长度。

现在我们来推导弧长公式的一般形式。

我们先对s进行平方，并展开成二项式的形式：s²=(Δx)²+(Δy)²=(Δx)²+(f(x+Δx)-f(x))²=(Δx)²+(f'(x)Δx+R(Δx))²其中f'(x)为f(x)的导数，R(Δx)为高阶无穷小。

将(s)²展开，得到：s²=(Δx)²+f'(x)²(Δx)²+2f'(x)R(Δx)Δx+R²(Δx)(Δx)²注意到R(Δx)是高阶无穷小，所以(R(Δx))²项可以忽略。

再次整理得：s²=(1+f'(x)²)(Δx)²+2f'(x)R(Δx)Δx将上述等式两边开平方，得到：s=√((1+f'(x)²)(Δx)²+2f'(x)R(Δx)Δx)现在我们要将s表示为x的函数。