史上详细的平面曲线的弧长公式计算微积分

弧长的计算公式
弧长的计算公式
弧长计算公式是一个数学公式，为L=n×π×r/180，L=α×r。

其中n是圆心角度数（角度制），r是半径，L是圆心角弧长，α是圆心角度数（弧度制）。

曲线的弧长也称曲线的长度，是曲线的特征之一。

不是所有的曲线都能定义长度，能够定义长度的曲线称为可求长曲线。

扇形面积公式
一条弧和经过这条弧两端的两条半径所围成的图形叫扇形（半圆与直径的组合也是扇形），它是由圆周的一部分与它所对应的圆心角围成。

S扇=LR/2（L为扇形弧长，R为半径）或π（R^2）*N/360（即扇形的度数）
扇形是与圆形有关的一种重要图形，其面积与圆心角（顶角）、圆半径相关，圆心角为n°，半径为r的扇形面积为n/360*πr^2.
如果其顶角采用弧度单位，则可简化为1/2×弧长×（半径）。

扇形还与三角形有相似之处，上述简化的面积公式亦可看成：1/2×弧长×（半径），与三角形面积：1/2×底×高相似。

弧微分的计算以弧微分的计算为标题，本文将介绍弧微分的概念、计算方法以及应用。

弧微分是微积分中的重要概念之一，它可以用于描述曲线的性质和计算曲线上的各种量。

通过了解弧微分的概念和计算方法，我们能更好地理解和应用微积分的知识。

让我们来了解一下弧微分的概念。

在平面直角坐标系中，我们可以用方程 y = f(x) 来表示曲线。

曲线上的每一个点都有唯一的坐标 (x, y)。

假设我们从曲线上的一个点 P1(x1, y1) 移动到另一个点 P2(x2, y2)，这两个点之间的直线距离称为弧长。

而弧微分就是描述这个弧长的微小变化。

弧微分的计算可以通过微积分中的导数来实现。

我们可以将曲线上的每一个点都看作一个参数 t 的函数，即 x = x(t) 和 y = y(t)，其中 t 是参数。

对于曲线上的任意两个点 P1(x1, y1) 和 P2(x2, y2)，我们可以将弧长表示为：s = ∫√(dx² + dy²)其中，dx 和 dy 分别表示 x 和 y 的微小变化。

根据导数的定义，我们可以得到：dx = x'(t)dtdy = y'(t)dt将 dx 和 dy 代入弧长的公式中，我们可以得到：s = ∫√(x'(t)²dt² + y'(t)²dt²)化简上式，我们可以得到：s = ∫√(x'(t)² + y'(t)²)dt这个公式描述了弧长和参数t 的关系，可以用来计算曲线上的弧长。

接下来，让我们看一下弧微分的计算方法。

根据弧微分的定义，我们可以得到：ds = √(dx² + dy²)将 dx 和 dy 代入上式中，我们可以得到：ds = √(x'(t)²dt² + y'(t)²dt²)化简上式，我们可以得到：ds = √(x'(t)² + y'(t)²)dt这个公式描述了弧微分和参数 t 的关系，可以用来计算弧微分。

牛顿-莱布尼茨公式是微积分中一个非常重要的公式，它可以用来计算曲线的弧长。

在学习微积分的过程中，我们经常会遇到需要计算曲线弧长的情况，而牛顿-莱布尼茨公式提供了一个非常便捷和有效的方法。

让我们来看一下牛顿-莱布尼茨公式的表达式：\[ L = \int_{a}^{b} \sqrt{1 + (f'(x))^2} dx \]这里，\( L \)代表曲线的弧长，\( f(x) \)代表曲线的函数，\( f'(x) \)代表函数的导数。

公式的核心是利用积分来求曲线的弧长，通过对曲线的微小线段进行求和，从而得到整条曲线的长度。

接下来，让我们以一条简单的曲线\( y = x^2 \)为例来演示牛顿-莱布尼茨公式的计算过程。

我们假设要计算曲线在区间[0, 1]上的弧长。

第一步，我们需要求出函数\( y = x^2 \)的导数\( f'(x) \)，即\( 2x \)。

我们将\( f'(x) \)带入到公式中，得到：\[ L = \int_{0}^{1} \sqrt{1 + (2x)^2} dx \]接下来，我们可以利用定积分的性质来求解这个积分。

通过简单的换元和分部积分，我们最终可以得到曲线\( y = x^2 \)在区间[0, 1]上的弧长为\( \frac{\sqrt{5} + \ln(2 + \sqrt{5})}{4} \)。

这个结果非常直观地展现了牛顿-莱布尼茨公式的应用。

不仅如此，牛顿-莱布尼茨公式还可以应用于更加复杂的曲线和函数。

无论是求解圆的弧长、椭圆的弧长，还是一些特殊函数的弧长，牛顿-莱布尼茨公式都能够提供一个通用的计算方法。

牛顿-莱布尼茨公式是微积分中非常重要的一个公式，它可以有效地计算曲线的弧长。

通过对曲线的微小线段进行求和，利用积分来得到整条曲线的长度，这个公式为我们提供了一个非常便捷和实用的工具。

在实际应用中，只要我们掌握了牛顿-莱布尼茨公式的计算方法，并灵活运用积分的性质，就可以轻松地解决曲线弧长的计算问题。

弧长计算公式在圆周长上的任意一段弧的长度叫做弧长。

有优弧劣弧之分。

弧长公式:n是圆心角度数，r是半径，a是圆心角弧度。

公式l = n（圆心角）x π（圆周率）x r（半径）/180在半径是R的圆中，因为360°的圆心角所对的弧长就等于圆周长C=2πR，所以n°圆心角所对的弧长为l=n°πR÷180°。

例：半径为1cm，45°的圆心角所对的弧长为l=nπR/180=45×π×1/180=45×3.14×1/180约等于0.785(cm)拓展扇形面积公式：S（扇形面积）=n（圆心角度数）x π（圆周率）x r²【半径的平方（2次方）】/360如果已知他的沿圆锥体的一条母线和侧面与下底面圆的交线将圆锥体剪开铺平，就得到圆锥的平面展开图。

它是由一个半径为圆锥体的母线长，弧长等于圆锥体底面圆的周长的扇形和一个圆组成的，这个扇形又叫圆锥的侧面展开图。

补充公式S扇=nπr*2/360=πrnr/360=2πrn/360×1/2r=πrn/180×1/2r所以：S扇=rL/2还可以是S扇=n/360πr²(n为圆心角的度数，L为该扇形对应的弧长。

)圆锥的表面积=圆锥的侧面积+底面圆的面积其中：圆锥体的侧面积=πRL圆锥体的全面积=πRl+πR2π为圆周率≈3.14R为圆锥体底面圆的半径L为圆锥的母线长我们把连接圆锥顶点和底面圆周上任意一点的线段叫作圆锥的母线（注意：不是圆锥的高）是展开扇形的边长n圆锥圆心角=r/l*360 360r/l弧长=圆周长侧面展开图的圆心角求法：n=360r/R=πRr或2πr=nπr/180 n=360r/R 。

如果题目中有切线，经常用的辅助线是链接圆心和切点的半径，得到直角，再用相关知识解题。

扇形的面积扇形是与圆形有关的一种重要图形，其面积与圆心角（顶角）、圆半径相关，圆心角为n°，半径为r的扇形面积为n/360*πr^2。

函数弧长计算公式函数弧长计算公式是用来计算一个曲线在给定区间上的弧长的公式。

弧长表示曲线的长度，它可以用来计算曲线的弯曲程度、曲线的曲率以及曲线的整体形状等。

在数学和物理学中，函数弧长计算公式是非常重要的一种工具，它被广泛应用于各个领域。

在平面上，考虑一个参数方程形式的曲线：x = f(t)和y = g(t)，其中t在[a, b]区间上变化。

现在我们希望计算这个曲线在[a, b]上的弧长。

为了得到一个近似的弧长，我们将[a, b]划分成n个小区间，并且在每个小区间上取一个代表点(ti, xi, yi)。

然后我们计算每一个小区间上的线段的长度，然后将它们加总得到近似的曲线弧长。

在一个小区间上，假设(xi, yi)和(xi+1, yi+1)是相邻的两个代表点。

那么这两个点之间的线段长度可以用勾股定理来计算：∆s = sqrt((xi+1 - xi)^2 + (yi+1 - yi)^2)这个线段长度代表了曲线在这个小区间上的弧长的近似值。

我们取n趋于无穷大的极限，就可以得到曲线在整个区间上的弧长。

为了计算这个极限，我们可以通过插值方法来逼近曲线上每个点的切线。

然后我们可以将曲线分割成n个小弧段，每个小弧段的弧长可以通过近似计算得到。

将这些小弧段的弧长相加，我们就可以得到整个曲线的弧长。

具体来说，函数弧长计算公式可以表示为：L = ∫[a, b] sqrt((dx/dt)^2 + (dy/dt)^2) dt其中(x(t), y(t))表示曲线上的点，x和y是t的函数，dx/dt和dy/dt分别表示x和y对t的导数。

这个公式是通过对曲线上的每个点的切线进行插值得到，并在整个区间上将这些切线的长度相加得到的。

需要注意的是，在实际应用中，函数弧长计算公式可能并不是那么容易计算。

在一些特殊的情况下，这个公式可以化简为更简单的形式。

例如，对于参数方程形式的曲线，如果函数的导数在[a,b]上是连续的，那么公式可以进一步简化为：L = ∫[a, b] sqrt((dx/dt)^2 + (dy/dt)^2) dt = ∫[a, b]sqrt((dx/dt)^2 + (dy/dt)^2) dt = ∫[a, b] sqrt(dx^2 + dy^2) dt 这就是参数方程形式的曲线的弧长计算公式。

曲线弧长长度计算公式在数学和物理学中，曲线的弧长长度是一个重要的概念。

它描述了曲线的长度，通常用于计算曲线上某一点到另一点的距离，或者描述曲线的整体长度。

曲线的弧长长度计算公式是一个基本的数学工具，它在许多领域都有着广泛的应用，包括工程、物理、计算机图形学等。

曲线的弧长长度计算公式可以通过积分来推导。

对于一个曲线上的点P(x, y)，我们可以将曲线分割成许多小段，每一小段都可以近似看作是一条直线。

假设我们将曲线分成n段，每一段的长度为Δs1, Δs2, ..., Δsn。

那么曲线的弧长长度可以近似表示为：L ≈Δs1 + Δs2 + ... + Δsn。

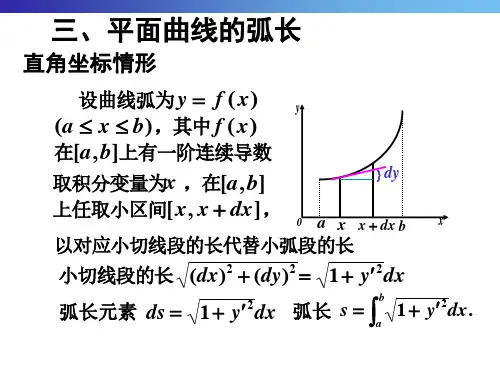
当我们将曲线分成无穷多小段时，每一小段的长度可以近似为0，这时曲线的弧长长度可以用积分来表示：L = ∫√(1 + (dy/dx)²) dx。

其中，dy/dx表示曲线在点P处的斜率，√(1 + (dy/dx)²)表示曲线在点P处的切线长度。

通过对曲线的弧长长度进行积分，我们可以得到曲线的整体长度。

曲线的弧长长度计算公式在实际应用中有着广泛的应用。

在工程领域，曲线的弧长长度计算公式可以用于计算曲线轨迹上的运动学参数，比如速度、加速度等。

在物理学中，曲线的弧长长度计算公式可以用于描述光线在介质中传播的路径，以及物体在空间中的轨迹。

在计算机图形学中，曲线的弧长长度计算公式可以用于生成平滑的曲线路径，以及对曲线进行优化和变形。

除了上述的应用，曲线的弧长长度计算公式还可以用于解决一些数学问题。

比如，我们可以通过曲线的弧长长度计算公式来求解曲线的最短路径问题，或者求解曲线的最优参数化问题。

曲线的弧长长度计算公式是一个非常强大的数学工具，它为我们解决各种问题提供了重要的数学基础。

在实际应用中，曲线的弧长长度计算公式可能会涉及到一些复杂的数学运算。

比如，对于一些复杂的曲线，我们可能需要使用数值方法来进行积分计算，或者使用数值逼近方法来近似表示曲线的弧长长度。

微积分弧长公式微积分弧长公式是一种研究形状和它们的性质的工具。

它允许人们测量几何形状的周长，这是一种古老的问题，可以回溯到古希腊数学家的时代。

弧长公式的概念和它的应用可以追溯到17世纪的十字军时代，此后在19世纪晚期到20世纪初受到改进和增强。

在欧几里德几何中，弧线是一个自然的对象，可以使用方程来描述。

通常，弧线与椭圆形和圆形相关，当它们被展示到平面时，它们的性质可以被描述为点的集合。

弧长公式是一个工具，可以用来测量弧形的长度，以及如何弯曲。

在数学中，弧长公式给出了特定形状的长度，根据特定函数的构成，其中一些函数对应于微积分中的函数。

比如，直线段的长度可以用一个单变量函数来表示，而圆弧的长度可以用一个双变量函数来表示。

另一方面，如果弧线是由方程来组成的，那么确定它的长度就变得更加复杂，因为每个变量都会影响弧线的形状。

定义一个函数f(x)的弧长可以用以下公式表示：L=∫a b[1+(f(x))2] dx要计算函数f(x)的弧长，首先要计算它的导函数f(x)，以及函数f(x)本身的实际值。

这样才能确定弧线的长度，从而知道特定形状的面积。

另外，微积分弧长公式不仅可以应用于几何图形，还可以用于其他数学问题，比如在无穷大极限中测量函数的行为、绘制无穷大曲线以及求解折线曲线的值等等。

例如，计算函数f(x)的弧长可以应用于推导椭圆的面积。

为了计算椭圆的面积，需要知道该椭圆的小轴和大轴长度，甚至需要知道它是圆形还是椭圆形等等。

可以用以下公式求解：面积=πab其中a是椭圆的小轴，b是椭圆的大轴。

使用椭圆的切线来求解小轴和大轴的长度可以有效的提高椭圆形面积的精确度，而通过弧长公式所求解的切线长度，可以大大提高计算椭圆形面积的准确性。

此外，在对信号进行处理的过程中，弧长公式也经常被用到。

在几何分析中，把信号转化成曲线形状，可以用来描述函数的特性，这需要计算曲线的弧长，以及它的切线长度。

总之，弧长公式是一个重要的公式，可以被用来计算特定形状的周长，从而推导出该形状的面积，它的应用非常广泛。

史上最详细的平面曲线的弧长公式计算微积分在微积分的广袤世界中，平面曲线的弧长公式是一个极为重要的概念和工具。

它不仅在数学理论中有着深刻的意义，还在众多实际应用中发挥着关键作用，从物理学中的运动轨迹到工程学中的曲线设计，都离不开对弧长的精确计算。

首先，让我们来直观地理解一下什么是弧长。

想象一条弯曲的曲线，比如一个圆弧或者更复杂的曲线，从曲线的一端到另一端的长度就是弧长。

但要精确地计算这个长度，可不是简单地用尺子去量，这就需要借助微积分的强大力量。

在数学中，我们通常用参数方程来描述平面曲线。

假设平面曲线由参数方程＄x ＝ x(t)＄，＄y ＝ y(t)＄给出，其中＄t$ 是参数，并且＄x(t)＄和＄y(t)＄都是连续可微的函数。

那么，弧长的计算公式可以表示为：＼L ＝＼int_{a}＾｛b} ＼sqrt{x'（t)＾2 ＋ y'（t)＾2} dt＼这里的＄x'（t)＄和＄y'（t)＄分别是＄x(t)＄和＄y(t)＄对＄t$ 的导数，＄a$ 和＄b$ 是参数＄t$ 的取值范围。

为了更好地理解这个公式，我们可以从微小的局部来考虑。

当参数＄t$ 有一个微小的增量＄dt$ 时，曲线对应的坐标会有微小的变化＄dx ＝ x'（t) dt$ 和＄dy ＝ y'（t) dt$ 。

根据勾股定理，这一小段曲线的长度可以近似表示为＄＼sqrt{（dx)＾2 ＋（dy)＾2} ＝＼sqrt{x'（t)＾2 ＋ y'（t)＾2} dt$ 。

然后，通过对这些微小的长度进行积分，就可以得到整个曲线的弧长。

接下来，我们通过几个具体的例子来看看如何应用这个公式。

例 1：考虑圆的参数方程＄x ＝ R ＼cos t$，＄y ＝ R ＼sin t$，其中＄R$ 是圆的半径，＄t$ 的取值范围是＄0, 2\pi$ 。

首先求导数：＄x'（t) ＝ R ＼sin t$，＄y'（t) ＝ R ＼cos t$ 。

弧长的积分公式：轮廓线的长度如何计算？弧长的积分公式是数学中的一种经典公式，在计算轮廓线、曲线、弧线、环线等长度时有着广泛的应用。

本文将介绍弧长的积分公式的概念、推导过程以及具体的计算方法，为读者提供科学的指导。

一、什么是弧长？弧长是指曲线上任意两点间的距离，通常用L表示。

例如，在一个圆形轮廓线上选取两个点，它们之间的弧长就是这条曲线上的弧长。

二、弧长的积分公式是什么？弧长的积分公式描述了曲线上三维空间中无数个微元长度的和。

假设曲线的参数为t，坐标为(x(t), y(t), z(t))，则曲线长度可以表示为以下积分形式：L = ∫[a, b]√[dx/dt]^2 + [dy/dt]^2 + [dz/dt]^2 dt其中，[a, b]代表积分区间，即曲线上参数t的取值范围。

√代表根号符号，dx/dt、dy/dt、dz/dt分别代表曲线参数t对应的偏导数。

三、如何计算弧长？弧长的计算过程具体如下：1. 确定曲线上取点的间距，越小越好。

2. 采用曲线上取点的间距计算曲线上的每个点与前一个点之间的距离。

3. 将步骤2中所得到的所有距离加起来，即可得到整个曲线的长度。

例如，考虑一个单位圆x^2 + y^2 = 1，对于任意一个参数t∈[0, 2π]，有：x(t) = cos(t)y(t) = sin(t)则弧长可以表示为：L = ∫[0, 2π]√[-sin(t)]^2 + [cos(t)]^2 dt= ∫[0, 2π] dt= 2π因此，单位圆的弧长为2π。

该结果与我们所知的单位圆的周长相符。

四、弧长的积分公式的应用弧长的积分公式可以帮助我们计算各种曲线、轮廓线、弧线、环线等的长度，从而广泛应用于数学、物理、工程等各个领域。

例如，在计算机图形学中，固定的弧长可以用来解决缺少参数曲线的问题。

总之，弧长的积分公式是一种非常实用、经典的数学公式，是计算各种曲线长度的重要工具之一。

读者可以通过本文的介绍，深入了解弧长的计算方法，从而在实际应用中更好地运用该公式。