第六章第二讲旋转体的体积与平面曲线的弧长

平面解析几何基础知识曲线的旋转体体积在平面解析几何中，曲线的旋转体体积是一个重要的概念。

在本文中，我们将介绍什么是曲线的旋转体体积，以及如何计算曲线的旋转体体积。

我们还会解释如何应用这一概念来解决一些实际问题。

一、曲线的旋转体体积的概念介绍在平面解析几何中，当一个曲线绕某一条直线旋转一周时，所形成的立体图形称为曲线的旋转体。

而曲线的旋转体体积就是这个立体图形的体积。

二、如何计算曲线的旋转体体积计算曲线的旋转体体积需要使用积分的方法。

具体而言，我们可以将曲线分割成无穷多个微小的弧段，然后将每个微小弧段旋转一周所形成的微小体积相加，从而得到整个旋转体的体积。

设曲线在直角坐标系中由函数y=f(x)(a≤x≤b)给出，将其绕x轴旋转一周。

则将曲线划分为无穷多个微小的弧段dx，每个微小的弧段dx所对应的体积元素为dV=πf^2(x)dx。

然后，对所有的微小弧段进行求和积分，即可得到曲线的旋转体体积V。

V=∫[a,b]πf^2(x)dx三、应用示例下面我们通过一个具体的应用示例来进一步说明如何计算曲线的旋转体体积。

例题：计算函数y=x^2在区间[0,1]上绕x轴旋转一周所形成的旋转体体积。

解答：根据前述的计算公式，我们可以得到函数f(x)=x^2在区间[0,1]上绕x轴旋转一周所形成的旋转体体积V为：V=∫[0,1]π(x^2)^2dx=∫[0,1]πx^4dx=π[1/5*x^5]从0到1=π/5所以，函数y=x^2在区间[0,1]上绕x轴旋转一周所形成的旋转体体积为π/5。

四、总结曲线的旋转体体积是平面解析几何中的重要概念，应用广泛。

通过使用积分的方法，我们可以计算曲线的旋转体体积。

在实际应用中，我们可以利用曲线的旋转体体积来解决一些具体的问题。

希望本文对您理解平面解析几何基础知识曲线的旋转体体积有所帮助。

（字数：525字）。

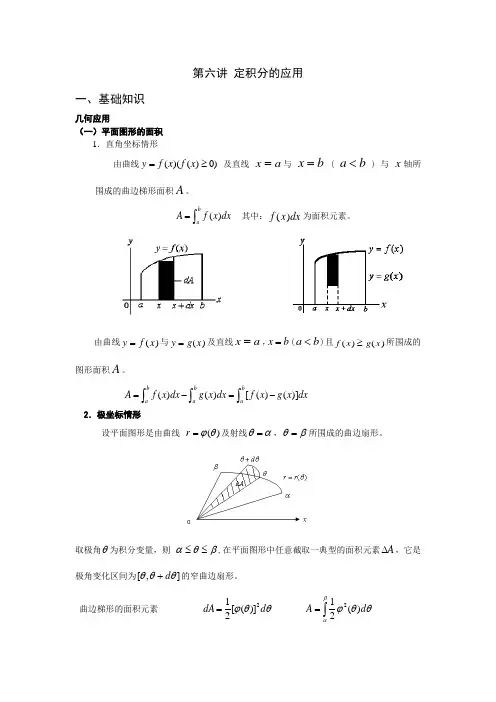
第六讲 定积分的应用一、基础知识几何应用（一）平面图形的面积 1．直角坐标情形由曲线)0)(()(≥=x f x f y 及直线 x a =与 x b = ( a b < ) 与 x 轴所围成的曲边梯形面积A 。

()baA f x dx =⎰ 其中：f x dx ()为面积元素。

由曲线y f x =()与y g x =()及直线x a =，x b =(a b <)且f x g x ()()≥所围成的图形面积A 。

()()[()()]=-=-⎰⎰⎰b b baaaA f x dx g x dx f x g x dx2．极坐标情形设平面图形是由曲线 )(θϕ=r 及射线αθ=，βθ=所围成的曲边扇形。

取极角θ为积分变量，则 βθα≤≤,在平面图形中任意截取一典型的面积元素A ∆，它是极角变化区间为],[θθθd +的窄曲边扇形。

曲边梯形的面积元素 θθϕd dA 2])([21= ⎰=βαθθϕd A )(212（二）旋转体的体积计算由曲线y f x =()直线x a =，x b =及x 轴所围成的曲边梯形，绕x 轴旋转一周而生成的立体的体积。

取x 为积分变量，则],[b a x ∈，对于区间],[b a 上的任一区间],[dx x x +，它所对应的窄曲边梯形绕x 轴旋转而生成的薄片似的立体的体积近似等于以)(x f 为底半径，dx 为高的圆柱体体积。

即：体积元素为 []dx x f dV 2)(π=所求的旋转体的体积为 []dx x f V ba⎰=2)(π（三）平面曲线的弧长 1.直角坐标情形设函数)(x f 在区间],[b a 上具有一阶连续的导数，计算曲线)(x f y =的长度s 。

取x 为积分变量，则],[b a x ∈,在],[b a 上任取一小区间],[dx x x +，弧长元素为[]dx x f ds 2)(1'+= 弧长为 []⎰'+=badx x f s 2)(12.参数方程的情形若曲线由参数方程)()()(βαφϕ≤≤⎩⎨⎧==t t y t x 给出，弧微分[][]dt t t dy dx ds 2222)()()()(φϕ'+'=+=则 [][]⎰'+'=βαφϕdt t t s 22)()(3.极坐标情形若曲线由极坐标方程)()(βθαθ≤≤=r r 给出，将极坐标方程化成参数方程，曲线的参数方程为x r y r ==⎧⎨⎩≤≤()cos ()sin ()θθθθαθβ，弧长元素为θθθθθθθd r r d r r d r r dy dx ds 22222222)()cos sin ()()sin cos ()()('+=+'+-'=+= 从而有 ⎰'+=βαθd r r s 22（四）.曲率与曲率半径 曲率记作,k 0lims d k s dsαα∆→∆==∆, 222''''tan '''sec sec 1'd d y y y y dx dx y ααααα=⇒=⋅⇒==+, 2''1'y d dx y α=+,又,ds =故322''(1')y d k dsy α==+.曲率半径 3221(1')''y k y ρ+==. 曲率圆二、例题1．平面图形的面积与旋转体的体积例 1. 已知抛物线2,y px qx =+(其中0,0p q <>)在第一象限内与直线5x y +=相切,且抛物线与x 轴所围成的平面图形的面积为s .问: (1)p q 和为何值时,s 达到最大值? (2)求出此最大值.【答案】,3p q =4=-5,22532s =例2.设⎪⎩⎪⎨⎧>≤=-0,0,)(22x ex e x F x x ，S 表示夹在x 轴与曲线()y F x =之间的面积. 对任何)(x f0t >，)(1t S 表示矩形t x t -≤≤，0()y F t ≤≤的面积. 求(I) 1()()S t S S t =-的表达式； (II) ()S t 的最小值.【答案】(I) t te t S 221)(--=，t ∈ (0 , +∞).(II) eS 11)21(-=. 例3.设曲线的极坐标方程为(0)a e a θρ=>,则该曲线上相应于θ从0到2π的一段弧与极轴所围成的图形的面积为41(1)4a e aπ-. 例 4.设1D 是由抛物线22y x =和直线x a =, 2x =及0y =所围成的平面区域; 2D 是由抛物线22y x =和直线x a =,0y =所围成的平面区域,其中02a <<.(1)试求1D 绕x 轴旋转而成的旋转体体积1V ;2D 绕y 轴旋转而成的旋转体体积2V . (2)问当a 为何值时,12V V +取得最大值?试求此最大值. 【答案】54(32)5a π- 4a π 1295π 例5.设曲线2(0,0)y ax a x =>≥与21y x =-交于点A ,过坐标原点O 和点A 的直线与曲线2y ax =围成一平面图形.问a 为何值时,该图形绕x 轴旋转一周所得的旋转体体积最大?最大体积是多少?【答案】4a =是体积最大,其最大体积为:522161518755V π=⋅= 例6.过坐标原点作曲线ln y x =的切线,该切线与曲线ln y x =及x 轴围成平面图形D . (1).求D 的面积A ;(2).求D 绕直线x e =旋转一周所得旋转体的体积V . 【答案】(1)112A e =- (2)2(5123)6V e e π=-+ 例7.（15-2） 设A>0，D 是由曲线段sin (0)2y A x x π=≤≤及直线0y =，2x π=所围成的平面区域，1V ，2V 分别表示D 绕x 轴与绕y 轴旋转成旋转体的体积，若12V V =，求A 的值.【答案】8π例8.(09-3-10 分)设曲线()y f x =，其中()y f x =是可导函数，且()0f x >，已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形，绕x 轴旋转一周所得的立体体积值是曲边梯形面积值的t π倍，求该曲线方程。

旋转体的表面积和体积计算旋转体是指通过绕某一轴旋转而形成的立体图形。

在几何学中，计算旋转体的表面积和体积是一种重要的技巧。

本文将介绍旋转体的表面积和体积计算方法，以及一些常见的旋转体示例。

一、旋转体的表面积计算方法要计算旋转体的表面积，我们可以使用定积分的方法。

设旋转体由曲线y=f(x)（0≤x≤a）绕x轴旋转而成，其中f(x)在闭区间[0,a]上连续且非负。

基于定积分的表面积计算公式为：S = 2π∫[a→0] y·ds其中，ds表示曲线的微小弧长。

在极坐标下，微小弧长ds可以表示为：ds = √(1+(dy/dx)²)·dx通过将dy/dx替换为f'(x)，我们可以将表面积计算公式简化为：S = 2π∫[a→0] f(x)·√(1+f'(x)²)·dx通过求解上述定积分，即可得到旋转体的表面积。

二、旋转体的体积计算方法旋转体的体积计算同样可以使用定积分的方法。

仍假设旋转体由曲线y=f(x)（0≤x≤a）绕x轴旋转而成。

体积计算公式为：V = π∫[a→0] y²·dx通过将y替换为f(x)，我们可以将体积计算公式写为：V = π∫[a→0] f(x)²·dx求解上述定积分即可得到旋转体的体积。

三、旋转体计算示例下面将以圆锥为例，演示旋转体的表面积和体积计算方法。

圆锥由一条斜边和底面形成，底面是一个半径为r的圆。

我们将底面放置在坐标轴上，圆锥的斜边与x轴的交点记为（0，h）。

要计算圆锥的表面积和体积，首先我们需要确定圆锥的方程。

通过类似三角函数的方法，我们可以得到圆锥的方程为：y = h/r·x其中，0≤x≤r，0≤h≤√(r²-x²)。

根据上述方程，我们可以计算出圆锥的表面积和体积。

四、总结通过本文的介绍，我们了解了旋转体的表面积和体积计算方法，并以圆锥为例进行了演示。

曲线的求弧长与旋转体体积教学方法总结曲线的求弧长与旋转体体积是高中数学中的重要内容，它们在几何和微积分领域中具有广泛的应用。

本文将总结一些教学方法，帮助学生更好地理解和应用这些概念。

一、曲线的求弧长教学方法1.引入概念：首先，我会向学生介绍曲线的概念和相关术语，包括曲线的参数方程、弧长元素以及弧长的定义。

通过例题演示，让学生了解如何根据参数方程求解弧长，并通过计算机绘图工具展示实际曲线的弧长。

2.数学推导：接下来，我会以数学推导的方式介绍弧长公式的推导过程，并解释其中的步骤和思路。

通过推导，学生能够更深入地理解弧长公式的来源和原理。

3.例题讲解：为了帮助学生掌握求解曲线弧长的方法，我会选择一些简单且具有代表性的例题进行讲解和演示。

在解题过程中，我会详细说明每一步的计算方法和思维逻辑，引导学生理解和掌握解题技巧。

4.实际应用：为了增加学生对曲线弧长的实际应用的认识，我会选取一些实际问题，如汽车行驶轨迹、物体的自由落体等，通过求解曲线的弧长来解决这些问题。

这样可以帮助学生将数学知识与实际问题相结合，提高学习兴趣和应用能力。

二、旋转体体积的教学方法1.引入概念：开始教学旋转体体积时，我会先向学生引入旋转体的概念和相关术语，如旋转轴、旋转面、截面积等。

通过具体的图形示例，让学生清楚地了解旋转体的定义和特点。

2.数学推导：接着，我会用数学推导的方式介绍旋转体体积的计算公式的推导过程。

通过推导和解释，学生能够理解体积公式的来源和原理，加深对旋转体体积的理解。

3.例题讲解：为了帮助学生掌握求解旋转体体积的方法，我会选择一些典型的旋转体例题进行讲解和演示。

在解题过程中，我会注重解题思路和关键步骤的讲解，并给予学生足够的时间来思考和尝试解题。

4.实际应用：为了增加学生对旋转体体积实际应用的认识，我会选择一些与实际问题相关的例题，如圆环、圆锥等，通过求解旋转体的体积来解决这些问题。

通过实际应用的例题，学生可以更好地理解旋转体体积的概念和计算方法，并将其应用于实际问题的解决中。

微积分应用曲线的弧长与旋转体的体积微积分作为数学的一个分支，广泛应用于各个领域中。

在微积分中，曲线的弧长与旋转体的体积是两个非常重要且常用的概念。

本文将分别介绍曲线的弧长以及旋转体的体积，并探讨它们在实际应用中的意义和计算方法。

曲线的弧长是指曲线上两点之间的路径长度，它在物理、几何、工程学等领域中有广泛的应用。

计算曲线的弧长需要使用积分方法，具体步骤如下：首先，确定曲线方程，并求出其导函数。

将导函数的绝对值表示为y'(x)，表示曲线在不同点上的斜率。

接着，选取一段曲线上的微小弧段Δs，该段的长度可以近似看作是线段的长度。

根据勾股定理，Δs在x轴和y轴上的投影分别为Δx和Δy。

然后，利用导函数y'(x)求得弧段Δs的长度。

根据导数的定义，Δs≈ √(Δx^2 + Δy^2) = √(1 + [y'(x)]^2) Δx。

最后，将弧段Δs的长度求和，即对Δs进行积分。

弧长L可以表示为积分的形式L = ∫√(1 + [y'(x)]^2)dx。

通过上述步骤，可以准确计算出曲线的弧长，这对于真实世界中的曲线问题，如公路的弯道长度、管道的弯曲区域长度等，具有重要的实际意义。

旋转体的体积是指通过绕定轴旋转曲线所形成的立体的体积。

计算旋转体的体积同样需要使用积分方法，具体步骤如下：首先，确定曲线方程，并确定该曲线绕哪个轴旋转，通常是x轴或y轴。

接着，将曲线分割成无限小的微小弧段，并将其旋转得到的微小体积ΔV表示为圆盘面积乘以微小高度。

然后，利用微积分的方法，将所有微小弧段的体积ΔV求和，即进行积分得到整个旋转体的体积V。

具体而言，对于绕x轴旋转的曲线，体积V可以表示为积分的形式V = π∫[y(x)]^2dx，其中y(x)为曲线方程。

而对于绕y轴旋转的曲线，体积V可以表示为积分的形式 V =π∫[x(y)]^2dy，其中x(y)为曲线方程。

通过以上计算方法，我们可以准确计算出绕任意轴旋转的曲线所形成的旋转体的体积。