下载文档原格式
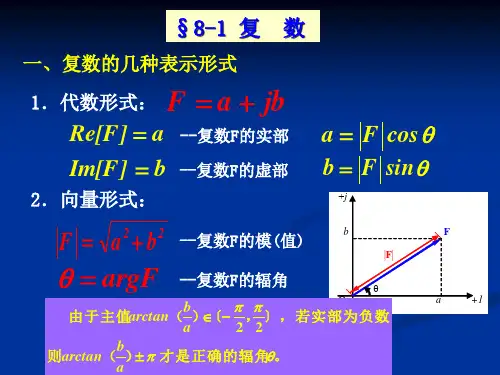
复数的代数形式及其运算第85课时课题：复数的代数形式及其运算一．教学目标：掌握复数的基本题型，主要是讨论复数的概念,复数相等,复数的几何表示,计算复数模，共轭复数，解复数方程等。
二．教学重点：复数的几何表示，计算复数模，共轭复数,解复数方程等。
三．教学过程:（一）主要知识：1．共轭复数规律，；2．复数的代数运算规律(1）i=1，i=i,i=1，i=i;(3)i・i・i・i=1，i＋i＋i＋i=0；；3．辐角的运算规律(1)Arg（z・z）＝Argz＋Argz（3）Arg=nAr gz(n∈N）.。
.，n1.或z∈R。
要条件是|z|＝|a|.（6）z・z≠0,则4．根的规律：复系数一元n次方程有且只有n个根，实系数一元n次方程的虚根成对共轭出现。
5．求最值时，除了代数、三角的常规方法外，还需注意几何法及不等式||z｜|z｜｜≤｜z±z｜≤｜z｜+|z|的运用.即｜z±z｜≤｜z|+|z|等号成立的条件是：z，z所对应的向量共线且同向。
|z±z|≥|z|｜z|等号成立的条件是：z,z所对立的向量共线且异向。
（二）范例分析Ⅰ.2004年高考数学题选1.(2004高考数学试题(浙江卷,6)）已知复数z1=3+4i, z2=t+i，且是实数，则实数t=（）A．B．C．?D．？2。
(2004年北京春季卷,2)当时，复数在复平面上对应的点位于（）A．第一象限B．第二象限 C．第三象限D．第四象限3.(2004年北京卷，2）满足条件的复数在复平面上对应点的轨迹是（ C ) A．一条直线B．两条直线C．圆D．椭圆Ⅱ.主要的思想方法和典型例题分析：1．化归思想复数的代数、几何、向量及三角表示，把复数与实数、三角、平面几何和解析几何有机地联系在一起，这就保证了可将复数问题化归为实数、三角、几何问题。
反之亦然。
这种化归的思想方法应贯穿复数的始终。
【分析】这是解答题，由于出现了复数和，宜统一形式,正面求解。
第三节 复数的代数形式及运算【目录】题型1 复数代数形式的运算 题型2 复数代数形式的综合应用三、解答题题型1 复数代数形式的运算1．计算：（1）54)31()22(i i -+； （2）1996)12(32132i ii-+++-。
解：（1）原式===-=+--+=-⋅+w wi i i i i 22)2()2321(2])1[()231(2)1(5252254i i 31)2321(2+-=+-。
（其中ω=i 2321+-）。
（2）原式=9989989982)22(])12[(321)321(i i i i i ii i +=-+=-+++=i+i 4×249+2=i+i 2=-1+i.2．设f(x, y)=x 2y-3xy+y 2-x+8，求：（1）f(1+i, 2-i)的值； （2）[f(2-5i, 2-5i)]-1的值。
解：（1）f(1+ i, 2-i)=(1+i)2·(2-i)-3(1+i)(2-i)+(2-i)2-(1+i)+8 =2i(2-i)-3(3+i)+(3-4i)-1-i+8=2+4i-9-3i+3-4i+7-i=3-4i ；（2）若x=y ，则f(x, y)=x 3-2x 2-x+8，又x=2-5i ，∴(x-2)2=(-5i)2，即x 2-4x+9=0，而x 3-2x 2-x+8=(x 2-4x+9)(x+2)-2x-10, ∴f(2-5i, 2-5i)=0-2(2-5i)-10=-14+25i,∴[f(2-5i, 2-5i)]-1=i i i 108510872165221614)52()14(521422--=--=+---. （3）∵(1-i 3)10=1-C 110·i 3+C 210·(i 3)2-C 310·(i 3)3+…，∴(1-i 3)10的展开式中奇数项之和为复数(1-i 3)10的实数。
又(1-i 3)10=[-2·10)]2321(i +-=210ω10=210ω=210)2321(i +-=-29+29i 3，∴(1-i 3)10的展开式中各奇数项的和为-29。
复数的代数形式与运算复数虽然在高考试题中的考察极为简单，但在强基或者联赛一试中考察的力度和难度都远高于高考.究其原因，复数已是现代数学研究主要的工具之一，不论是在工程中的应用还是在基础研究中的应用中，例如傅里叶变换，著名的黎曼猜想等均与复数有关.同时，复数还和其他板块如三角，向量等有着重要的联系.综上所述，复数是中学数学中重要的内容之一，肯定也是强基或联赛的考察热点.本节开始，我们将系统地介绍强基或联赛难度的复数及其应用，从而更好地让大家认识复数，用好复数！首先来讲复数的的概念与重要性质，这一讲主要包括复数的代数形式及运算，共轭复数及性质.一．主要知识1.复数的代数形式.复数：bi a z +=（R b a ∈,），其中a 为实部，b 为虚部.记作：a z =)Re(表示bi a z +=的实部，b z =)Im(表示bi a z +=的虚部.2.复数相等的条件.代数形式下，两个非零复数相等，当且仅当实部相等且虚部相等.三角形式下，两个非零复数相等，当且仅当它们的模与幅角主值分别相等.3.共轭复数.bi a z +=（R b a ∈,）它的共轭复数为bi a z -=，显然z z =.下面梳理共轭复数的重要性质.（1）z z z ⋅=2||（2）2121z z z z ±=±（3）2121z z z z ⋅=（4）2121)(z zz z =（5）)Im(2),Re(2z i z z z z z =-=+（6）)Im(||),Re(||z z z z ≥≥（7）z 为实数的充要条件为z z =，z 为虚数的充要条件为)0(,≠-=z z z .3.代数形式下复数的运算：关于代数形式下复数的运算是高考必考内容，相对简单，大家练得都比较熟练，我们在此处就不再赘述.4.几个重要的性质：（1）2212212121||||z z z z z z z --+=+（2）)1)(1(123++-=-z z z z ；)1)(1(123+-+=+z z z z .（3）虚数单位的周期性.二．典例分析1.代数形式下复数的基本运算例1.已知复数z 满足ii z -=-112，则复数z 在复平面内的点到原点的距离为_______.解析：由121z i i-=-，得1115221(1)(1)22i z i i i i i i +=+=+=+--+，故该复数在复平面内的点的坐标为15,22⎛⎫ ⎪⎝⎭2=．例2.已知复数z 满足i z z +=+2||2，求||z 解析：设bi a z +=，R b a ∈,，所以，i b a b a )1(2222-+-=+，解得：1=b ，0=a 或者34-=a .例3.若复数z 满足1||=z ，则|))((|i z i z -+的最大值为_________解析：设,,z a bi a b R =+∈，则()()()22()()111z i z i a b i a b i a b +-=+-+-=+-⎡⎤⎡⎤⎣⎦⎣⎦，故()()z i z i +-=，其中[]1,1b ∈-.当1b =-时，max ()()2z i z i +-=.例4.设复数R i z i z ∈⋅+=+=ααα,cos 1,2sin 21.则||||132121iz z iz z f -+-=的最小值为___.解析：令12z iz t -===，则t ⎡∈⎣，且此时有()222212sin cos 310sin212z iz t ααα+=-+=-=-.故2212121312z iz t f z iz t-++==≥-.当1t =，即()4k k Z παπ=-∈时，f 的最小值为2.例5.复数13=z ，则=+++202223z z z ________.解析：由13=z 得0)1)(1(2=++-z z z ，所以1=z ，或者012=++z z .因此可得：25202223=+++z z z 或19202223=+++z z z .2.共轭复数及其应用例6.证明：虚数成对定理，即设虚数z 是实系数方程00111=++++--a x a xa x a n n nn 的根，则z 也是这个实系数方程的根.证明：因为z 是方程的根，所以00111=++++--a z a za z a n n nn ，两边同时取共轭得：00111=++++--a z a za z a n n n n ，即00111=++++--a z a za z a n n nn .因此z 也是这个实系数方程的根.由第一部分可知，共轭运算和四则运算是可以交换顺序的，那么利用共轭运算便可不必设出复数的具体形式，这样可避免有时因为代入具体形式而导致的复杂运算.这样的想法可使用于条件中包含模长或共轭复数的情况.例7.已知13z =，25z =，127z z -=，求12z z .解析：由127z z -=1212()()49z z z z ⇒--=22112212()49z z z z z z ⇒-++=122115z z z z ⇒+=-下面将等式两边同乘12z z ，有2221112215z z z z z z ⋅+=-⋅，由于22222225z z z z ==，故21122225915z z z z ⋅+=-⋅2112225()1590z z z z ⇒⋅+⋅+=解得123331010z i z =-±.注：当使用共轭复数计算有关问题时，类似与圆锥曲线中整体代入的思想来进行计算，此时不必考虑具体表示形式，减少运算，下面再看一例.例8.已知复数21,z z 满足i z z z z -=-==223,3||,2||2121，求21z z 的值.解析：由于3||,2||21==z z ，故可得：9,42211==z z z z ，于是我们将i z z -=-22321可进一步表示为：i z z z z i z z z z z z -=-⇒-=⋅-⋅2)32(61221311*********.那么，i i i z z i z z i z z 52451826123261232612121221+-=---=--=--=.注：此题若用具体形式计算，可能过程会很麻烦！例9.复数z 满足1||<z 且25|1|=+z z ，则=||z （）A.54 B.43 C.32 D.21解析：42511(=++z z z z ，所以425111=+++z z z ，整理可得0417)(42=+-z z z z ，解得41=z z 或者4=z z .由于1||<z ，进一步可得：21||=z .例10.（2015高联一试）已知复数数列}{n z 满足)(1,111++∈++==N n ni z z z n n ，则2015z 的值为__________.解析：本题需要找寻递推关系，依题可得：i z i n ni z i n z i n z z n n n n n ++=+-++++=+-+=+++=+++2)1(11)1(1)1(1112，故可得：i z z n n +=-+22.那么i z z i z z i z z +=-⋅⋅⋅+=-+=-2,,2,2132011201320132015，由累加法可得：i z 100720152015+=.3.综合应用这一部分难度较大，综合各种性质和方法，读者应细心体会.例11.（2018浙江预赛）已知虚数z 满足013=+z ，则=-+-2018201811()1(z z z _______.解析：由三次方程因式分解可知：()()3221011010z z z z z z +=⇒+-+=⇒-+=，整理可得：()()()67232201820182018220181345231111111z z z z z z z z z z z+++⎛⎫⎛⎫+====- ⎪⎪---⎝⎭⎝⎭.例12.（2020浙江预赛）已知复数z 满足1||=z ，当|13|234++++z z z z 取最小值时，求复数z 的值.解析：依题可得：31113|13|222234234++++=++++=++++z z zz z z z z z z z z z ，利用完全平方公式得：43|1Re 2Re 4||1()(|3112222≥++≥++++=++++z z z z z z z z z z 等号成立时，i z 41541±-=.例13．复数z 满足1z =，且使得关于x 的方程20x z x z +⋅+=有实根，则这样的复数z 的个数为（）A．1个B．2个C．3个D．4个解析：设i,,z a b a b R =+∈，因为1z =，所以221a b +=，所以将i,,z a b a b R =+∈代入方程20x z x z +⋅+=整理()()2i 0x ax a b bx +++-=，因为关于x 的方程20x z x z +⋅+=有实根，所以200x ax a b bx ⎧++=⎨-=⎩，所以当0b =时，解得1a =±，此时关于x 的方程为210x x ++=或210x x --=，易知方程210x x ++=无实数根，故舍去，所以1z =-；当0b ≠时，解得1x =，12a =-，所以2b =±，所以122z =-±，此时方程有实数根1x =，满足条件.综上，1i 22z =-±或1z =-.故这样的复数z 的个数为3个.。
复数代数形式的加减运算及其几何意义复数是由实数和虚数组成的数，可以表示为 a + bi 的形式，其中 a 和 b 都是实数，i 是虚数单位，满足 i^2 = -1、复数代数形式的加减运算是指复数之间的加法和减法操作。
复数加法运算：设有两个复数 z1 = a + bi 和 z2 = c + di，其中 a、b、c、d 都是实数。
复数加法运算的计算规则如下：1.实部相加：(a+c)2.虚部相加：(b+d)因此，两个复数之和为 z1 + z2 = (a + bi) + (c + di) = (a + c) + (b + d)i。
复数减法运算：设有两个复数 z1 = a + bi 和 z2 = c + di，其中 a、b、c、d 都是实数。
复数减法运算的计算规则如下：1.实部相减：(a-c)2.虚部相减：(b-d)因此，两个复数之差为 z1 - z2 = (a + bi) - (c + di) = (a - c) + (b - d)i。
综上所述，复数的加减运算可以分别对实部和虚部进行相应的加减操作，从而得到新的复数。
几何意义：复数可以用平面上的向量来表示，其中复数的实部对应向量在 x 轴上的投影，虚部对应向量在 y 轴上的投影。
对于复数 z = a + bi，可以将其在平面上表示为一个点 P(x, y)。
- 复数加法的几何意义：设有两个复数 z1 = a + bi 和 z2 = c + di，根据复数加法运算规则，z1 + z2 = (a + c) + (b + d)i。
可以将其几何意义理解为将向量 z2 平移至向量 z1 的尾部，得到一个新的向量。
新向量的坐标为 (a + c，b + d)。
因此，复数加法可以看作是两个向量的矢量相加。
- 复数减法的几何意义：设有两个复数 z1 = a + bi 和 z2 = c + di，根据复数减法运算规则，z1 - z2 = (a - c) + (b - d)i。
复数基木概念内容：1. 虚数单位i ：/ =-1,及运算.2. 复数概念.复数分类.'实数@ = 0)'纯虚数(a = 0)非纯虚数(aHO)复数的两种表示：(1)代数形式：z=a+bi (a,b£R)・⑵几何表示：复平面上对应的点Z(a ・b)和向量(立・ 复数z=a+bi (a.bGR)与点Z(a.b)是一一对应关系. a = cb = d特姝的：a + bi = 0<^> a = b = 0(a.b e R).共轨复数：z = a+bi(a,b w R), z = a-bi其对应点关于x 轴对称，以0为起点的对应向量也关于x 轴对称•共轨复数的运算及性质: Z] ± Z2 = Z] ± Z 分； Z] • Z” = Z] •乙；(―)== (“ H 0)5 Z2z + zeR ・ z■ z e 7?・复数的模：表示复数的有向线段的长度叫做向量的模 I z 1= yla 2 +b 2.运算及性质I z 2 I|l Zi I — 1 g l| V § + z? IV 可 I +1 G Iz-z=lzl 2=lzl 2要求：了解数的概念的发展，理解虚数单位及其运算、复数的概念、分类及表示方法、复 数相等的概念，并能利用它们解决简单问题.掌握共轨复数、复数模的概念及运算和性质，并 能解决有关的简单问题. 例题：例1・计算,+产+尸+・・・・・・ + Z 2003分析与解答：利用连续四项和为零的性质较方便.共2003项，每连续四项和为0,余3项・(从后而数较 方便)・•••原式=/+z 2+z 3=z-l-/=-l.3. 4. 向虽貶是可以平行移动的.复数相等：a 初 i=c+di 、 5. 6. 或将此式看成等比数列求和问题，则也用到了：严=1,严利=i,严=一1,严3=_jgZ).分析与解答：要利用模的概念及运算. 13 + 4/11血一、伤 1•偏例 3.若虚数(m2+l)+(m2-m)i 与虚数2+(-l+m)i 是共轨虚数，求实数m 值. 分析与解答：根据共轨复数的概念有当m=l 时,m ・m=l ・m=O,两个数均为实数，舍去,当m=l 时，符合题意，所以m=-l ・注意题目中是虚数这一条件，使得虚部不为零.例4・a.b 均为复数，有以下几个结论：⑴若lal=lbl,则 a=±b (2)7T7T =16/1(3)\a-b\= (a-b)1 则有(). A 、都正确B 、仅⑵正确C 、(2),(3)正确D 、都不正确分析与解答： 要注意，a.b 是复数这一条件.lai 即a 的模，是实数，且lal^O, ：./^=\a\正确.而lal=lbl 时，a.b 若为虚数a=±b 不正确•而la-bl 为实数，但(a-b)2不一泄是实数，故B 正确. 例5.设ZGC,且lzl=2,求ll-^ + zl 的最大和最小值.分析与解答：因为题目有模岀现，可根据||可I 一1 6 1| § Z, +0已© I + 1 ° I 来解决最值问题.由于 |ll-V3/l-lzl|<ll-V3/ + ^l<ll-V3/l + lzL••• l2-2l<ll-V3/ + zl<2 + 20<ll-V3z + zl<41-?1-z 2 2例2・求 (3 + 4i)迈-冋 _2‘的模 例2・求 _2,的模・m=± 1.•••原式的模=J(⑸+2? =3.m 2 +1 = 2〜・•・ll-J気+zl的最大值为4,最小值为0. 其它解法见后. 例6・已知：eC, I可1=1,求・1 -分析与解答：此题应利用复数模及共馳复数的性质.由121|=1,可知©・云=1 (••• z-z=lzl2=lzl2)原式二】=1.。
复数代数形式的四则运算【要点梳理】要点一、复数的加减运算1.复数的加法、减法运算法则： 设1z a bi =+，2z c di =+（,,,a b c d R ∈），我们规定：12()()()()z z a bi c di a c b d i +=+++=+++21()()z z c a d b i -=-+-要点诠释：（1）复数加法中的规定是实部与实部相加，虚部与虚部相加，减法同样。
很明显，两个复数的和（差）仍然是一个复数，复数的加（减）法可以推广到多个复数相加（减）的情形．（2）复数的加减法，可模仿多项式的加减法法则计算，不必死记公式。
2.复数的加法运算律:交换律：z 1+z 2=z 2+z 1结合律:：(z 1+z 2)+z 3=z 1+(z 2+z 3)要点二、复数的加减运算的几何意义1. 复数的表示形式：代数形式：z a bi =+（,a b R ∈）几何表示：①坐标表示：在复平面内以点(,)Z a b 表示复数z a bi =+（,a b R ∈）； ②向量表示：以原点O 为起点，点(,)Z a b 为终点的向量OZ 表示复数z a bi =+.要点诠释：复数z a bi =+←−−−→一一对应复平面内的点(,)Z a b ←−−−→一一对应平面向量OZ 2．复数加、减法的几何意义：如果复数1z 、2z 分别对应于向量1OP 、2OP ，那么以1OP 、2OP 为两边作平行四边形12OPSP ，对角线OS 表示的向量OS 就是12z z +的和所对应的向量.对角线21P P 表示的向量21P P 就是两个复数的差12z z -所对应的向量.设复数z 1=a +bi ，z 2=c +di ，在复平面上所对应的向量为1OZ 、2OZ ，即1OZ 、2OZ 的坐标形式为1OZ =(a ，b )，2OZ =(c ，d )以1OZ 、2OZ 为邻边作平行四边形OZ 1ZZ 2，则对角线OZ 对应的向量是OZ ，由于OZ =1OZ +2OZ =(a ，b )+(c ，d )=(a +c ，b +d )，所以1OZ 和2OZ 的和就是与复数(a +c )+(b +d )i对应的向量类似复数加法的几何意义，由于z 1－z 2=(a －c )+(b －d )i ，而向量12Z Z = 1OZ -2OZ =(a ，b )-(c ，d )=(a -c ，b -d )，所以1OZ 和2OZ 的差就是与复数(a －c )+(b －d )i 对应的向量要点诠释：要会运用复数运算的几何意义去解题，它包含两个方面：（1）利用几何意义可以把几何图形的变 换转化成复数运算去处理（2）反过来，对于一些复数运算式也可以给以几何解释，使复数做为工具运用于几何之中。
复数的运算法则1.复数的表示形式（1）代数形式共轭复数F*=a-jb在数学中虚单位常用i表示，如F=a+bi，但由于在电路中已用i表示电流，故虚单位改用j表示。
实部(real part)：Re[F] = a；虚部(imaginary part)：Im[F] = b。
复数可用复平面上的向量表示(如图所示)。
（2）三角形式F=|F|(cosθ+jsinθ)|F|为复数的模，θ为复数的幅角，θ=argF。
则|F|=θ=arctan(b/a)。
且a=|F|cosθ，b=|F|sinθ 。
（3）指数形式(exponential form)（4）极坐标形式(polar form)F=|F|<θ2.复数的基本运算（1）加减运算复数的加减运算采用代数形式较为简便，或在复平面中使用平行四边形法则。
设F1 = a1 + jb1，F2 = a2 + jb2，有平行四边形法则：（2）乘除运算复数的乘除运算使用指数形式或极坐标形式较为简便。
①指数形式即复数乘积的模等于各复数模的积；辐角等于各复数辐角的和。
②极坐标形式（3）旋转因子复数ejθ = cosθ + jsinθ = 1∠θFejθ →复数F逆时针旋转一个角度θ ，模不变+j ，–j，-1 都可以看成旋转因子。
若一个复数乘以j，等于在复平面上把该复数逆时针旋转π/2。
若一个复数除以j ，等于把该复数乘以-j ，则等于在复平面上把该复数顺时针旋转π/2。
（4）相等运算两个复数相等必须满足：复数的实部、虚部分别对应相等；或者复数的模和辐角分别对应相等。
若F1 = F2，则必须有或。
