(湖北版02期)2014届高三数学 名校试题分省分项汇编专题001 集合与常用逻辑用语(含解析)理 新人教A版

（湖北版01期）2014届高三数学 名校试题分省分项汇编专题01 集合与常用逻辑用语（含解析）理 新人教A 版一．基础题组1.【湖北省教学合作2014届高三10月联考数学试题理科数学】已知集合={x||x|2,x Z}A ≤∈，1={x|>0,x R}1B x ∈+，则A B 是（ ）A ．(1,2]-B ．[0,2]C ．{1,0,1,2}-D ．{0,1,2}2.【2013年湖北七市（州）高三年级联合考试理科数学】下列说法中不正确的个数是 （ ）①命题“∀x ∈R ，123+-x x ≤0”的否定是“∃0x ∈R ，12030+-x x >0”； ②若“p ∧q ”为假命题，则p 、q 均为假命题；③“三个数a ，b ，c 成等比数列”是“b=ac ”的既不充分也不必要条件 A ．O B ．1 C ．2 D ．33.【湖北省黄冈市黄冈中学2013届高三下学期6月适应性考试数学理试题（B 卷）】已知集合{2,0,1}A =，集合{|||B x x a =<，且}x Z ∈，则满足A B ⊆的实数a 可以取的一个值是( )A ．0B ．1C ．2D ．34.【湖北省黄冈市黄冈中学2013届高三下学期6月适应性考试数学理试题（B卷）】已知命题p ：,x R使1sin2x x成立．则p为（）A．,x R1sin2x x均成立 B．,x R1sin2x x均成立C．,x R使1sin2x x成立 D．,x R使1sin2xx成立5.【湖北省荆门龙泉中学2014届高三年级8月月考数学（理科）试卷】下列有关命题的说法正确的是 ( )A．命题“若21x=，则1=x”的否命题为：“若21x=，则1x≠”．B．“1x=-”是“2560x x--=”的必要不充分条件．C．命题“∃,Rx∈使得210x x++<”的否定是：“对∀,Rx∈均有210x x++<”．D．命题“若x y=，则sin sinx y=”的逆否命题为真命题．【答案】D【解析】试题分析：A中，否命题应为若12≠x，则1≠x；B中，1-=x⇒2560x x--=，应为充分不必要条件；C中，命题的否定应为：对∀,Rx∈均有012≥++xx；Ｄ中，原命题为真，则逆否命题也为真.考点：命题的否定；四种命题．6.【湖北省荆门龙泉中学2014届高三年级8月月考数学（理科）试卷】钱大姐常说“便宜没好货”,她这句话的意思是:“不便宜”是“好货”的 （ ）条件. A ．充分 B ．必要 C ．充要 D ．既不充分也不必要7.【湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考理科数学】已知全集{}1,2,3,4,5,6,7,8,9U = 集合{}1,2,3,4,5,6A = 集合{}3,4,5,6,7,8B =，则集合UUAB为（ ）A.{}3,4,5,6B.{}1,2,7,8,9C.{}1,2,3,4,5,6,7,8D.{}9【答案】D 【解析】试题分析：解法一：因为全集{}1,2,3,4,5,6,7,8,9U =，集合{}1,2,3,4,5,6A = 集合{}3,4,5,6,7,8B =，所以{}7,8,9UA =，{}1,2,9UB =，故{}9UUAB =，故选D ；解法二：因为全集{}1,2,3,4,5,6,7,8,9U =，集合{}1,2,3,4,5,6A = 集合{}3,4,5,6,7,8B =，所以{}1,2,3,4,5,6,7,8A B =，故(){}9UUUA B A B ==，故选D.考点：1.集合的交集；2,.集合的补集运算8.【湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考理科数学】命题“对任意x R ∈都有21x ≥”的否定是（ ） A.对任意x R ∈，都有21x <B.不存在x R ∈，使得21x <C.存在x R∈，使得201x ≥ D.存在0x R∈，使得201x < 9.【湖北省重点中学2014届高三10月阶段性统一考试理科数学】已知全集U R =，设集合(){}ln 31A x y x ==-，集合(){}sin 2B y y x ==+，则()UA B为（ ）A.1,3⎛⎫+∞ ⎪⎝⎭ B.10,3⎛⎤ ⎥⎝⎦ C.11,3⎡⎤--⎢⎥⎣⎦D.∅考点：1.对数函数的定义域；2.三角函数的值域；3.集合的补集与交集运算10.【湖北省重点中学2014届高三10月阶段性统一考试理科数学】已知命题:p x R ∃∈，2lg x x ->，命题:q x R ∀∈，sin x x <，则 （ ）A.命题p q ∨是假命题B.命题p q ∧是真命题C.命题()p q ⌝∧是真命题 D.命题()p q ⌝∨是假命题11.【湖北省重点中学2014届高三10月阶段性统一考试理科数学】在ABC ∆中，“()()sin cos cos sin 1A B B A B B -+-≥”是 “ABC ∆是直角三角形”的（ ）A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件不必要条件，故选A.考点：1.两角和的正弦公式；2.充分必要条件12.【湖北孝感高中2014届高三年级九月调研考试数学（理）】已知全集U R =，集合{}021x A x =<<，{}3log0B x x =>，则()U A C B =（ ）A ． {}1x x >B ．{}0x x >C ．{}01x x <<D ．{}0x x <13.【湖北孝感高中2014届高三年级九月调研考试数学（理）】已知命题p ：020,log 1x R x +∃∈=，则p ⌝是（ ）A ． *2,log 1x R x ∀∈≠ B ．*2,log 1x R x ∀∉≠ C ．*020,log 1x R x ∃∈≠D ．*020,log 1x R x ∃∉≠14.【湖北孝感高中2014届高三年级九月调研考试数学（理）】满足{}1234M a a a a ⊆，，，，且{}{}12312Ma a a a a =，，，的集合M 的个数是（ ）A ．1B ．2C ．3D ．415.【湖北孝感高中2014届高三年级九月调研考试数学（理）】“0a b >>”是“222a b ab +<”的 （ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件16.【湖北稳派教育2014届高三10月联合调研考试数学理科试题】已知集合}1|{-==x y x A ，}1001,lg |{≤≤==x x y x B ，则=B A （ ）A. ]100,1[B.]2,1[C. ]2,0[D. )10,0[ 【答案】B 【解析】试题分析：依题意[1,)A =+∞，[0,2]B =，∴[1,2]A B =，故选B.考点：函数的定义域，值域，交集.17.【2013届高中毕业生四月调研理科数学测试题】命题“若220x y +=，则0x y ==”的否命题是（ ）A. 若220x y +=，则 x 、y 中至少有一个不为0B. 若220x y +≠，则 x 、y 中至少有一个不为0 C. 若220x y +≠，则 x 、y 都不为0 D. 若220x y +=，则 x 、y 都不为018.【湖北省教学合作2014届高三10月联考数学试题理科数学】不等式组|21|32113xxx-<⎧⎪+⎨≤⎪-⎩的解集为 .二．能力题组1. 【湖北省教学合作2014届高三10月联考数学试题理科数学】下列给出的四个命题中，说法正确的是（）A．命题“若21x=，则1x=”的否命题是“若21x=，则1x≠”；B．“1x=-”是“2560x x--=”的必要不充分条件；C．命题“存在x R∈，使得21x x++<”的否定是“对任意x R∈，均有210x x++<”；D．命题“若x y=，则sin sinx y=”的逆否命题为真.2.【湖北稳派教育2014届高三10月联合调研考试数学理科试题】给出下列命题：①命题“01R2>++∈∀xxx，的否定是：01R,2<=+∈∃xxx；②命题“若0=ab，则0=a或0=b”的否命题是“若0≠ab，则0≠a且0≠b”；③x ∃、R ∈y ，y x y x sin sin )sin(-=-；④向量a ，b 均是单位向量，其夹角为θ，则命题“1|:|>-b a p ”是命题“]65,2[:ππθ∈q ”的充要条件.其中正确的命题的个数是（ ）A. 4B. 3C.2D.1 【答案】C 【解析】试题分析：R ∈∀x ，012>++x x 的否定应为R ∈∃x ，012≤++x x ，故①错；②正确；③正确；21cos 21121)(1:222<⇒<⋅⇒>+-⇒>-⇒>-θb a b b a a b a b a p ],3(ππθ∈⇒，从而⇒∈)65,2[:ππθq 1:>-b a p ，反之不成立，故④错．考点：全程命题，特称命题，充要条件.3.【湖北稳派教育2014届高三10月联合调研考试数学理科试题】在整数集Z 中，被5整除所得余数为k 的所有整数组成一个“类”，记为}Z |5{][∈+=n k n k ，4,3,2,1,0=k ，给出如下三个结论： ①]4[2014∈； ②]2[2∈-；③]4[]3[]2[]1[]0[Z =；、④“整数a 、b 属于同一“类”的充要条件是“]0[∈-b a ”.其中，正确结论的个数是（ ）A. 0B. 1C. 2D. 34.【湖北省荆门龙泉中学2014届高三年级8月月考数学（理科）试卷】已知22{||4},{1(41)2}A x x aB x og x x =-<=-->（1）若a =l ，求 A B ；（2）若AB R =，求实数a 的取值范围．【答案】(1)AB ={}13|-<<-x x ;(2) .31<<a【解析】 试题分析：（１）把a ＝１代入Ａ和Ｂ，解不等式，再取交集即可.（２）把Ａ和Ｂ先解出来，然后再取A B R =，从而求出.试题解析：(1)当1=a 时，Ａ＝{},53|<<-x x Ｂ＝{}.51|>-<x x x 或∴{};13|<<-=⋂x x B A（２）{},44|+<<-=a x a x A {}.51|>-<=x x x B 或且R B A =⋃，∴.31<<a 考点：1、不等式的解法；２、集合的关系及运算.5.【湖北省重点中学2014届高三10月阶段性统一考试理科数学】已知():sin cos r x x x m+>；()2:10s x x mx ++>，如果x R ∀∈，()r x 与()s x 有且仅有一个是真命题，求实数m 的取值范围.6.【湖北孝感高中2014届高三年级九月调研考试数学（理）】已知命题p：不等式11x m->-的解集为R，命题q：()()52=-xf x m是(,)-∞+∞上的增函数，若p或q为真命题，p且q为假命题，求实数m的取值范围．7.【湖北稳派教育2014届高三10月联合调研考试数学理科试题】已知命题]2,1[:∈∀x p ，02≥-a x ，命题R :0∈∃x q ，使得01)1(020<+-+x a x .若“p 或q 为真”，“p 且q 为假”，求实数a 的取值范围.【答案】3>a 或11≤≤-a .【解析】试题分析：有条件求出命题p 、q 为真的a 的取值范围，再由p 或q 为真，p 且q 为假， 则p 与q 一真一假，分两种情况求出结论.试题解析：由条件知，2x a ≤对]2,1[∈∀x 成立，∴1≤a ；∵R 0∈∃x ，使得01)1(020<+-+x a x 成立. ∴不等式01)1(020<+-+x a x 有解，∴04)1(2>--=∆a ，解得3>a 或1-<a ；（6分）∵p 或q 为真，p 且q 为假，∴p 与q 一真一假．①p 真q 假时，11≤≤-a ；②p 假q 真时，3>a .∴实数a 的取值范围是3>a 或11≤≤-a . （12分） 考点：复合命题的真假，函数三．拔高题组1.【湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考理科数学】已知命题:p 方程2220a x ax +-=在[]1,1-上有解，命题:q 函数()22f x x ax =+2a +的值域为[)0,+∞，若命题“p 或q ”是假命题，求实数a 的取值范围.2.【湖北孝感高中2014届高三年级九月调研考试数学（理）】已知}04|{2=+=x x x A , }01)1(2|{22=-+++=a x a x x B ，其中a R ∈，如果A∩B=B，求实数a 的取值范围．⑴当B =∅时，224(1)4(1)0a a ∆=+--<，解得1a <-； …………5分。

（湖北版02期）2014届高三数学 名校试题分省分项汇编专题004 三角函数与三角形（含解析）理 新人教A 版一．基础题组1.【湖北省部分重点高中2014届高三11月联考】函数sin()(0)y x πϕϕ=+>的部分图象如图所示,设P 是图象的最高点,,A B 是图象与x 轴的交点,记APB θ∠=,则sin2θ的值是（ ） A ．1665B ．6365C ．1663-D ．1665-2.【湖北省部分重点中学2014届高三第一次联考数学】设ABC ∆的内角A ，B ，C 所对的边分别为c b a ,,，若三边的长为连续的三个正整数，且C B A >>，C A 2=，则CB A s i n :s i n :s i n为（ ）A ．4:3:2B ．5:4:3C ．6:5:4D ．7:6:5∴)1(2)1()1()1(21222+--++⋅-=+n n n n n n n ，解得5=n ，∴61=+n ，41=-n ， ∴4:5:6::=c b a ，由正弦定理得4:5:6sin :sin :sin =C B A ，选C.考点：正弦定理、余弦定理、二倍角的正弦公式.3.【黄冈中学 黄石二中 鄂州高中2014届高三三校联考】要得到一个奇函数，只需将x x x f cos 3sin )(-=的图象（ ）A 、向右平移6π个单位 B 、向右平移3π个单位 C 、向左平移3π个单位 D 、向左平移6π个单位4.【湖北省八校联考】△ABC 中，角,,A B C 成等差数列是sin sin )cos C A A B =+成立的（ ）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.【武汉市2014届高三11月调研测试】已知函数f (x )＝⎩⎪⎨⎪⎧2x 3，x ﹤0，－tan x ，0≤x ＜π2．则f (f (π4))＝ ．6.【湖北省部分重点高中2014届高三11月联考】（选修4-1：几何证明选讲）AB 是半圆O 的直径，点C 在半圆上，CD AB ⊥，垂足为D ，且5AD DB =，设COD θ∠=，则tan θ的值为 .7.【黄冈中学 黄石二中 鄂州高中2014届高三三校联考】若1cos cos -=βα，则)sin(βα+＝考点：三角函数求值．8.【湖北省八校联考】将函数sin(2)y x ϕ=+的图象向左平移4π个单位后得到的函数图象关于点4(,0)3π成中心对称，那么||ϕ的最小值为 .二．能力题组1.【武汉市2014届高三11月调研测试】已知函数f (x )＝cos x sin2x ，下列结论中错误的是（ ）A ．y ＝f (x )的图象关于点(π，0)中心对称B ．y ＝f (x )的图象关于直线x ＝π2对称C ．f (x )的最大值为32D ．f (x )既是奇函数，又是周期函数(2)cos(2)sin 2(2)cos sin 2()f x x x x x f x πππ+=++==，故周期是2π，故D 正确；对于C 选项，2.【黄冈中学 黄石二中 鄂州高中2014届高三三校联考】已知函数x x f 2sin 1)(π+=，若有四个不同的正数i x 满足M x f i =)(（M 为常数），且8<i x ，)4,3,2,1(=i ，则4321x x x x +++的值为（ ）A 、10B 、14C 、12D 、12或2020．考点：三角函数图像与性质．3.【湖北省部分重点中学2014届高三第一次联考数学】 在△ABC 中，边，，2AB 1AC == 角32A π=，过A 作P BC AP 于⊥，且μλ+=，则=λμ .又0=∙，4.【湖北省八校联考】已知向量2(2sin(),2)3xπω=+a，(2cos,0)xω=b(0)ω>，函数()f x=⋅a b的图象与直线2y=-π．（Ⅰ）求ω的值；（Ⅱ）求函数()f x在[0,2]π上的单调递增区间．5.【武汉市2014届高三11月调研测试】设△ABC的内角A，B，C的对边分别为a，b，c，(a ＋b＋c)(a－b＋c)＝ac．（Ⅰ）求B；（Ⅱ）若sin A sin C＝3－14，求C．【答案】（I）23π；（II）12π或4π.【解析】考点：1.余弦定理；2.两角的和差公式.6.【湖北省部分重点高中2014届高三11月联考】（本小题满分12A 是△ABC 的内角．（1）求角A 的大小；（2）若BC =2，求△ABC 面积S 的最大值，并判断S 取得最大值时△ABC 的形状.7.【湖北省部分重点中学2014届高三第一次联考数学】已知函数)4(2cos )12(212sin 3)(ππf x f x x f '+'+=. （1）求)(x f 的最小正周期和最小值；（2）若不等式3|)(|<-m x f 对任意⎥⎦⎤⎝⎛∈3,12ππx 恒成立，求实数m 的取值范围.（2）有（1）知2)62sin(2)(-+=πx x f ，当]6,12(ππ∈x 时]65,3(62πππ∈+x ， ∴]1,21[)62sin(∈+πx ，则0)(1≤≤-x f ， …………8分三．拔高题组1.【黄冈中学 黄石二中 鄂州高中2014届高三三校联考】已知ABC ∆的三内角A 、B 、C 所对的边分别是a ，b ，c ，向量)cos 1,(sin B B -=与向量)0,2(=的夹角θ的余弦值为21 （Ⅰ）求角B 的大小； （Ⅱ）若3=b ，求c a +的范围。

湖北省部分重点中学2014届高三第二次联考高三数学试卷（理科）参考答案CDDDBCACBB②和③ 3或13 2(0,]3 216．解：（Ⅰ）∵()2π3πcos 2cos 22cos 22323f x x x x x x ⎛⎫⎛⎫=--=-=- ⎪ ⎪⎝⎭⎝⎭， ∴.故函数()f x 的最小正周期为π；递增区间为5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦(k ∈Z )（Ⅱ）解法一：π23B f B ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭，∴π1sin 32B ⎛⎫-=- ⎪⎝⎭． ∵0πB <<，∴ππ2π333B -<-<，∴ππ36B -=-，即π6B =． 由余弦定理得：2222cos b a c ac B =+-，∴2132a a =+-⨯，即2320a a -+=，故1a =（不合题意，舍）或2a =． 因为222134b c a +=+==，所以∆ABC 为直角三角形.解法二：π23B f B ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭，∴π1sin 32B ⎛⎫-=- ⎪⎝⎭． ∵0πB <<，∴ππ2π333B -<-<，∴ππ36B -=-，即π6B =．由正弦定理得：1πsin sin 6a A ==，∴sin C =，∵0πC <<，∴π3C =或2π3． 当π3C =时，π2A =；当2π3C =时，π6A =．（不合题意，舍） 所以∆ABC 为直角三角形. 17.(Ⅰ) 延长AD ，FE 交于Q ．因为ABCD 是矩形，所以BC ∥AD ，所以∠AQF 是异面直线EF 与B C 所成的角．在梯形ADEF 中，因为DE ∥AF ，AF ⊥FE ，AF＝2，DE ＝1得∠AQF ＝30°．(Ⅱ) 方法一：设AB ＝x ．取AF 的中点G ．由题意得DG ⊥AF ．因为平面ABCD ⊥平面ADEF ，A B ⊥AD ，所以AB ⊥平面ADEF ，(第17题图)所以AB ⊥DG ．所以DG ⊥平面ABF ．过G 作GH ⊥BF ，垂足为H ，连结DH ，则DH ⊥BF ，所以∠DHG 为二面角A －BF －D 的平面角．在直角△AGD 中，AD ＝2，AG ＝1，得DG．在直角△BAF 中，由AB BF ＝sin ∠AFB ＝GH FG ，得GH x， 所以GH．在直角△DGH 中，DG，GH，得DH＝． 因为cos ∠DHG ＝GH DH ＝13，得x所以AB方法二：设AB ＝x ．以F 为原点，AF ，FQ 所在的直线分别为x 轴，y 轴建立空间直角坐标系Fxyz ．则 F (0，0，0)，A (－2，0，0)，E0，0)，D (－10)，B (－2，0，x )， 所以DF ＝(1，0)，BF ＝(2，0，－x )．因为EF ⊥平面ABF ，所以平面ABF 的法向量可取1n ＝(0，1，0)．设2n ＝(x 1，y 1，z 1)为平面BFD 的法向量，则111120,0,x z x x -=⎧⎪⎨-=⎪⎩ 所以，可取2n ＝，1． 因为cos<1n ，2n >＝1212||||n n n n ⋅⋅＝13，得 x所以AB18．解：（1）当1n =时，由111211a S a -=⇒=.又1121n n a S ++-=与21n n a S -=相减得：12n n a a +=，故数列{}n a 是首项为1，公比为2的等比数列，所以12n n a -=（2）设n a 和1n a +两项之间插入n 个数后，这2n +个数构成的等差数列的公差为(第17题图)n d ， 则11211n n n n a a d n n -+-==++， 又(12361)611952,2014195262+++++=-=， 故61616220146262262(621)2612.6363b a d =+-⋅=+⨯=⨯ 19 0.41,11120.41712.a b a b ++=⎧⎨+⨯+=⎩解得：0.5,0.1a b ==.（Ⅱ）X 2 的可能取值为4.12,11.76,20.40.()[]2 4.12(1)1(1)(1)P X p p p p ==---=-，()[]22211.761(1)(1)(1)(1)P X p p p p p p ==--+--=+-，()220.40(1)P X p p ==-.………9分（Ⅲ）由（Ⅱ）可得：()222 4.12(1)11.76(1)20.40(1)E X p p p p p p ⎡⎤=-++-+-⎣⎦ 211.76p p =-++. ………………11分因为E(X 1)< E(X 2)， 所以21211.76p p <-++.所以0.40.6p <<.当选择投资B 项目时，p 的取值范围是()0.4,0.620．解：（1）依题意，得2a =，c e a == 1,322=-==∴c a b c ；故椭圆C 的方程为2214x y += ． （2）方法一：点M 与点N 关于x 轴对称，设),(11y x M ，),(11y x N -， 不妨设01>y ．由于点M 在椭圆C 上，所以412121x y -=． （*） 由已知(2,0)T -，则),2(11y x TM +=，),2(11y x TN -+=，21211111)2(),2(),2(y x y x y x TN TM -+=-+⋅+=⋅∴3445)41()2(1212121++=--+=x x x x 51)58(4521-+=x ． 由于221<<-x ，故当581-=x 时，TM TN ⋅取得最小值为15-． 方法二：点M 与点N 关于x 轴对称，故设(2cos ,sin ),(2cos ,sin )M N θθθθ-， 不妨设sin 0θ>，由已知(2,0)T -，则)sin ,2cos 2()sin ,2cos 2(θθθθ-+⋅+=⋅TN TM3cos 8cos 5sin )2cos 2(222++=-+=θθθθ51)54(cos 52-+=θ． 故当4cos 5θ=-时，TM TN ⋅取得最小值为15-，此时83(,)55M -， (3) 方法一：设),(00y x P ，则直线MP 的方程为：)(010100x x x x y y y y ---=-， 令0y =，得101001y y y x y x x R --=， 同理：101001y y y x y x x S ++=， 故212021202021y y y x y x x x S R --=⋅ （**）又点M 与点P 在椭圆上，故)1(42020y x -=，)1(42121y x -=，代入（**）式，得： 4)(4)1(4)1(421202*********202021=--=----=⋅y y y y y y y y y y x x S R ． 所以4=⋅=⋅=⋅S R S R x x x x OS OR ，OR OS +的最小值为4 方法二：设(2cos ,sin ),(2cos ,sin )M N θθθθ-，不妨设sin 0θ>，)sin ,cos 2(ααP ，其中θαsin sin ±≠．则直线MP 的方程为：)cos 2(cos 2cos 2sin sin sin αθαθαα---=-x y ，令0y =，得θαθαθαsin sin )sin cos cos (sin 2--=R x ， 同理：θαθαθαsin sin )sin cos cos (sin 2++=S x ， 故4sin sin )sin (sin 4sin sin )sin cos cos (sin 42222222222=--=--=⋅θαθαθαθαθαS R x x ． 所以4=⋅=⋅=⋅S R S R x x x x OS OR ，OR OS +的最小值为421、解：（I ）'121()(1)2(1)(1)[(1)2]n n n n f x nx x x x x x n x x --=---=---， 当1[,1]2x ∈时，由'()0n f x =知1x =或者2n x n =+， 当1n =时，11[,1]232n n =∉+，又111()28f =，(1)0n f =，故118a =； 当2n =时，11[,1]222n n =∈+，又211()216f =，(1)0n f =，故2116a =； （II ）当3n ≥时，1[,1]22n n ∈+， ∵1[,)22n x n ∈+时，'()0n f x >；(,1)2n x n ∈+时，'()0n f x <； ∴()n f x 在2n x n =+处取得最大值，即2224()()22(2)n n n n n n a n n n +==+++ 综上所述，21,(1)84,(2)(2)n n n n a n n n +⎧=⎪⎪=⎨⎪≥⎪+⎩． 当2n ≥时，欲证 2241(2)(2)n n n n n +≤++，只需证明2(1)4n n+≥ ∵011222222(1)()()()n n n n n n n C C C C n n n n+=+⋅+⋅++⋅ 2(1)41212142n n n-≥++⋅≥++=，所以，当2n ≥时，都有21(2)n a n ≤+成立． （III ）当1,2n =时，结论显然成立；当3n ≥时，由（II ）知3411816n n S a a a =+++++2221111181656(2)n <++++++ 11111111()()()816455612n n <++-+-++-++ 1117816416<++=． 所以，对任意正整数n ，都有716n S <成立．。

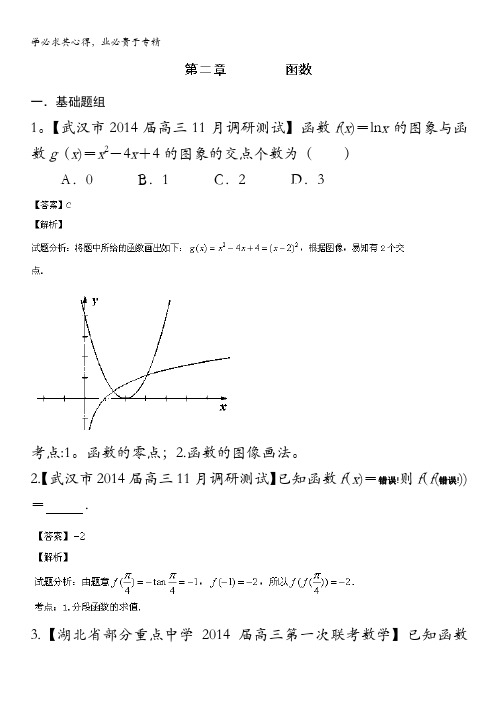
一．基础题组1。

【武汉市2014届高三11月调研测试】函数f(x)＝ln x的图象与函数g（x)＝x2－4x＋4的图象的交点个数为（）A．0 B．1 C．2 D．3考点:1。

函数的零点；2.函数的图像画法。

2.【武汉市2014届高三11月调研测试】已知函数f（x)＝错误!则f（f(错误!))＝．3.【湖北省部分重点中学2014届高三第一次联考数学】已知函数)(x f y =的定义域为{}5,83|≠≤≤-x x x 且,值域为{}0,21|≠≤≤-y y y 且。

下列关于函数)(x f y =的说法：①当3-=x 时，1-=y ；②将)(x f y =的图像补上点()0,5，得到的图像必定是一条连续的曲线；③)(x f y =是[)5,3-上的单调函数;④)(x f y =的图象与坐标轴只有一个交点。

其中正确命题的个数为（ ）A. 1 B 。

2 C. 3 D 。

4二．能力题组1.【湖北省部分重点中学2014届高三第一次联考数学】 已知函数)(x f 是定义在()()+∞∞-,00, 上的偶函数，当0>x 时,()⎪⎩⎪⎨⎧>-≤<-=-2,22120,12)(|1|x x f x x f x ，则函数1)(4)(-=x f x g 的零点个数为（ ）A 。

4 B. 6 C. 8 D. 10当32≤<x 时，函数)(x f 递减且)21,21[)(-∈x f ，43≤<x 时，函数)(x f 递减且2。

【湖北省部分重点高中2014届高三11月联考】如图，偶函数)(x f 的图像形如字母M ，奇函数)(x g 的图像形如字母N,若方程：,0))((,0))((==x g f x f f0))((,0))((==x f g x g g 的实根个数分别为a 、b 、c 、d ，则d c b a +++=（ ）A ． 27B ． 30C ．33D ． 363。

【湖北省部分重点高中2014届高三11月联考】定义][x 表示不超过x的最大整数，记{}][x x x -=，其中对于3160≤≤x 时，函数1}{sin ][sin )(22-+=x x x f 和函数{}13][)(--⋅=xx x x g 的零点个数分别为.,n m 则（ )A ．314,101==n mB ．313,101==n mC ．313,100==n mD ．314,100==n m131+=x y 在)4,3[∈x 有一个交点,在)5,4[∈x 有一个交点，,在)316,315[∈x 有一个交点，共有313个，故313=n 。

一．基础题组1.【广东省中山市一中2014届高三第二次统测】已知集合{}M=，1,2,3 {}=∈<<，则（)14N x Z xA. NM N= M⊆B。

N M=C。

{2,3}D. (1,4)M N=2.【广东省中山市实验高中2014届高三11月阶段考试】设集合{}B=--，则()2,1,2A B等于( ）2,1,0,1,2A=,{}1,2U=--，{}UA。

{}1B。

{}1,2 C.{}2D。

{}0,1,23。

【广东省仲元中学、中山一中、南海中学、潮阳一中、宝安中学、普宁二中2014届高三第一次联考】设U R=，集合{}==∈，A y y x R2,x{}240=∈-≤，则下列结论正确的是（)B x Z xA.()A B=+∞0,B.()(],0A B=-∞UC.(){}2,1,0A B=--UD。

(){}1,2A B=U4。

【广东省增城市2014届高三调研考试】设集合{}U=，集1,2,3,4,5,6,7合{}2,4,5A=,集合B={}A B=1,3,5,7，则()U( )A。

{}5 B.{}2,4,52,4C。

{}D。

{}2,4,65.【广东省惠州市2014届高三第二次调研考试】设集合{3213}A x x =-≤-≤,集合B 为函数lg(1)y x =-的定义域，则A B =( ）A 。

(1,2)B 。

[1,2]C 。

[1,2)D 。

(1,2]6.【广东省执信中学2014届高三上学期期中考试】设全集U R =，集合(){}30A x x x =+<，集合{}1B x x =<-，则下图中阴影部分表示的集合为（ ) A 。

{}31x x -<<- B.{}30x x -<< C.{}0x x >D 。

{}1x x <-7。

【广东省深圳市宝安区2014届高三调研考试】已知集合{}1,2,3,4,5,6U =，集合{}1,2,3,4P =，{}3,4,5Q =,则()UP Q = （ ）A 。

一．基础题组1.【湖北省黄冈市黄冈中学2013届高三下学期6月适应性考试数学理试题（B 卷）】在区间[－1,1]上随机取一个数x ，则sin4xπ的值介于12-与2之间的概率为( )A ．14B ．56C ．13D ．232.【湖北省黄冈市黄冈中学2013届高三下学期6月适应性考试数学理试题（B 卷）】气象意义上从春季进入夏季的标志为：“连续5天的日平均温度均不低于22 0C ”．现有甲、乙、丙三地连续5天的日平均温度的记录数据（记录数据都是正整数）： ① 甲地：5个数据的中位数为24，众数为22； ② 乙地：5个数据的中位数为27，总体均值为24；③ 丙地：5个数据中有一个数据是32，总体均值为26，总体方差为10.8； 则肯定进入夏季的地区有 ( )A ． 3个B ．2个C ．1个D ． 0个3.【湖北省黄冈市黄冈中学2013届高三下学期6月适应性考试数学理试题（B 卷）】从,,,,a b c d e 这5个元素中取出4个放在四个不同的格子中，且元素b 不能放在第二个格子中，问共有 种不同的放法．（用数学作答） 【答案】96 【解析】试题分析：利用间接法，435496A A -=.考点：排列问题.4.【湖北荆州中学高三年级第一次质量检测数学试卷理科数学】若随机变量(1,4)xN ，(0)P x m ≤=，则(02)P x <<=（ ）A . 12m - B.12m - C. 122m- D. 1m -5.【湖北荆州中学高三年级第一次质量检测数学试卷理科数学】从某高中随机选取5名高三男生，其身高和体重的数据如下表所示：根据上表可得回归直线方程^^0.56y x a =+，据此模型预报身高为172cm 的高三男生的体重为 ( )A ．70.09kgB ．70.12kgC ．70.55kgD ．71.05kg 【答案】B 【解析】6.【湖北荆州中学高三年级第一次质量检测数学试卷理科数学】在区间[,]ππ-内随机取两个数分别记为,a b ，则使得函数22()2f x x ax b π=+-+ 有零点的概率为 （ ） A .78 B. 34 C. 12 D. 147.【2013届高中毕业生四月调研理科数学测试题】对某商店一个月内每天的顾客人数进行统计，得到样本的茎叶图（如图所示），则该样 本的中位数、众数、极差分别是（ ）A. 46,45,56B. 46,45,53C. 47,45,56D. 45,47,53 【答案】A【解析】试题分析：由茎叶图知，共有30个数，中位数为4547462+=，众数为45，极差681256-=，故选A.考点：茎叶图，中位数、众数、极差的定义.8.【湖北荆州中学高三年级第一次质量检测数学试卷理科数学】甲、乙两种水稻试验品种连续4年的单位面积平均产量如下：其中产量比较稳定的水稻品种是 .9.【湖北荆州中学高三年级第一次质量检测数学试卷理科数学】把一枚硬币任意抛掷三次，事件A = “至少一次出现反面”，事件B = “恰有一次出现正面”求(|)P B A = .【答案】37【解析】试题分析：由题意，333()28P AB ==，317()128P A =-=，所以3()38(|)7()78P AB P B A P A ===，故答案为37.考点：条件概率.二．能力题组1.【湖北省黄冈市黄冈中学2013届高三下学期6月适应性考试数学理试题（B卷）】节日期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后得到如下图的频率分布直方图.(1)此调查公司在采样中,用到的是什么抽样方法?(2)求这40辆小型车辆车速的众数和中位数的估计值;(3)若从车速在[80,90)的车辆中任抽取2辆,求抽出的2辆车中车速在[85,90)的车辆数ξ的分布列及数学期望.⨯+⨯+⨯+⨯-=,解得97.5x0.0150.0250.0450.06(75)0.5x= ,2.【湖北荆州中学高三年级第一次质量检测数学试卷理科数学】某市统计局就本地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（每个分组包括左端点，不包括右端点，如第一组表示月收入在[1000,1500)，（单位：元）．（Ⅰ）估计居民月收入在[1500,2000)的概率；（Ⅱ）根据频率分布直方图估计样本数据的中位数；（Ⅲ）若将频率视为概率，从本地随机抽取3位居民（看做有放回的抽样），求月收入在[1500,2000)的居民数X的分布列和数学期望．【答案】（1）0.2；（2）2400；（3）分布列详见解析，0.9.3.【2013届高中毕业生四月调研理科数学测试题】某工厂生产甲、乙两种电子产品，甲产品的正品率为80% ,次品率为20% ;乙产品的正品率为90%，次品率为10%.生产1件甲产品，若是正品则可盈利4万元，若是次品则亏损1万元;生产1件乙产品,若是正品则可盈利6万元,若是次品则亏损2万元.设生产各件产品相互独立.(1)记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润，求X的分布列与数学期望；(2)求生产4件甲产品所获得的利润不少于10万元的概率.【答案】（1）E X()8.2（2）0.8192三．拔高题组1.【2013年湖北七市（州）高三年级联合考试理科数学】2013年2月20日，针对房价过高，国务院常务会议确定五条措施(简称“国五条”)．为此，记者对某城市的工薪阶层关于“国五条”态度进行了调查，随机抽取了60人，作出了他们的月收入的频率分布直方图(如图)，同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表)：(I)试根据频率分布直方图估计这60人的平均月收入；(Ⅱ)若从月收入(单位：百元)在[15，25)，[25，35)的被调查者中各随机选取3人进行追踪调查，记选中的6人中不赞成“国五条”的人数为X ，求随机变量X 的分布列及数学期望．338733995(0)18C C P X C C ==⋅= 23312878273333999917(1)36C C C C C P X C C C C ==⋅+⋅=。

一．基础题组1.【湖北省部分重点高中2014届高三11月联考】已知集合⎭⎬⎫⎩⎨⎧=+=14922y x x M ，⎭⎬⎫⎩⎨⎧=+=123y x y N ，则=⋂N M （ ） A 、∅ B 、{})0,2(),0,3( C 、 ]3,3[- D 、{}2,32.【湖北省部分重点高中2014届高三11月联考】下列命题中是假命题．．．的是 （ ） A ．,)1()(,342是幂函数使+-⋅-=∈∃m m xm x f m R ),0(+∞且在上递减 B ．有零点函数a x x x f a -+=>∀ln ln )(,02C ．βαβαβαsin cos )cos(,,+=+∈∃使R ;D ．,()sin(2)f x x ϕϕ∀∈=+R 函数都不是偶函数1sin )0(±==ϕf ，故不是任意的ϕ，D 对；故选D.考点：1.基本初等函数；2.函数的单调性；3.函数的奇偶性3.【武汉市2014届高三11月调研测试】给定两个命题p ，q ．若﹁p 是q 的必要而不充分条件，则p 是﹁q 的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件4.【湖北省部分重点中学2014届高三第一次联考数学】已知两个集合{})2ln(|2++-==x x y x A ，⎭⎬⎫⎩⎨⎧≤-+=012|x e x x B ，则=B A （ ）. A. )2,21[- B. ]21,1(-- C. ),1(e - D. ),2(e5.【湖北省部分重点中学2014届高三第一次联考数学】已知命题p :所有素数都是偶数，则p ⌝是（ ）A.所有的素数都不是偶数B.有些素数是偶数C.存在一个素数不是偶数D. 存在一个素数是偶数【答案】C【解析】试题分析：已知命题p :所有素数都是偶数，则p ⌝是“存在一个素数不是偶数”，选C. 考点：全称命题的否定.6.【黄冈中学 黄石二中 鄂州高中2014届高三三校联考】设{}62|≤≤=x x A ，{}32|+≤≤=a x a x B ，若A B ⊆，则实数a 的取值范围是（ ）A 、[]3,1B 、),3[+∞C 、),1[+∞D 、()3,17.【湖北省八校联考】集合2{3,log }P a =，{,}Q a b =，若{0}PQ =,则P Q =（ ）A.{3,0}B.{3,0,2}C.{3,0,1}D.{3,0,1,2}8.【湖北省八校联考】下列命题，正确的是（ ）A.命题:x ∃∈R ，使得210x -<的否定是：x ∀∈R ，均有210x -<.B.命题：若3x =,则2230x x --=的否命题是：若3x ≠，则2230x x --≠.C.命题：存在四边相等的四边形不是正方形，该命题是假命题.D.命题：cos cos x y =，则x y =的逆否命题是真命题.【答案】B【解析】9.【湖北省八校联考】△ABC 中，角,,A B C 成等差数列是sin sin )cos C A A B =+成立的（ ）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件二．能力题组1.【黄冈中学 黄石二中 鄂州高中2014届高三三校联考】有下述命题①若0)()(<⋅b f a f ，则函数)(x f 在),(b a 内必有零点；②当1>a 时，总存在R x ∈0，当0x x >时，总有x x a a n x log >>；③函数)(1R x y ∈=是幂函数；④若A B ，则)()(B Card A Card < 其中真命题的个数是（ ）A 、0B 、1C 、2D 、3＞1）在区间(0,)+∞上都是增函数，但它们的增长速度不同，而且不在同一个‘档次’上，随着x 的2.【黄冈中学 黄石二中 鄂州高中2014届高三三校联考】已知、为非零向量，则“⊥”是“函数)()()(x x x f -∙+=为一次函数”的（ ）A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件3.【黄冈中学 黄石二中 鄂州高中2014届高三三校联考】已知命题p ：函数x a y )1(-=在R 上单调递增；命题q ：不等式13>-+a x x 的解集为R ，若q p ∨为真，q p ∧为假，求实数a 的取值范围．试题解析：若p 真，则211>⇒>-a a 2分。

2014年普通高等学校招生全国统一考试（湖北卷）数学（理科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的。

1.为虚数单位，则=+-2)11(ii （ ） A. 1- B. C. i - D. i【答案】C【解析】试题分析：因为122)11(2-=-=+-iii i ，故选C 。

【点评】本题考查复数的运算，容易题。

2. 若二项式7)2(x a x +的展开式中31x的系数是84，则实数=a （ ） A.2 B. 54 C. 1 D.42答案】D【解析】试题分析：因为r r r r rrr x a C xax C 2777772)()2(+---⋅⋅⋅=⋅⋅，令327-=+-r ，得2=r ，所以84227227=⋅⋅-a C ，解得42=a ，故选D 。

【点评】本题考查二项式定理的通项公式，容易题。

3. 设U 为全集，B A ,是集合，则“存在集合C 使得C C B C A U ⊆⊆,是“∅=B A ”的（ ） A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件 【答案】A【解析】试题分析：依题意，若C A ⊆，则A C C C U U ⊆，当C C B U ⊆，可得∅=B A ；若∅=B A ，不能推出C C B U ⊆，故选A 。

【点评】本题考查集合与集合的关系，充分条件与必要条件判断，容易题。

得到的回归方程为a bx y+=ˆ，则（ ） A.0,0>>b a B.0,0<>b a C.0,0><b a D.0.0<<b a 【答案】B【解析】试题分析：依题意，画散点图知，两个变量负相关，所以0<b ，0>a .选B 。

【点评】本题考查根据已知样本数判断线性回归方程中的b 与a 的符号，容易题。

5.在如图所示的空间直角坐标系xyz O -中，一个四面体的顶点坐标分别是（0,0,2），（2,2,0），（1,2，1），（2,2,2），给出编号①、②、③、④的四个图，则该四面体的正视图和俯视图分别为（ ）A. ①和②B.③和①C. ④和③D.④和② 【答案】D【解析】试题分析：在坐标系中标出已知的四个点，根据三视图的画图规则判断三棱锥的正视图为④与俯视图为②，故选D 。

（湖北版01期）2014届高三数学 名校试题分省分项汇编专题01 集合与常用逻辑用语（含解析）理 新人教A 版一．基础题组1.【湖北省教学合作2014届高三10月联考数学试题理科数学】已知集合={x||x|2,x Z}A ≤∈，1={x|>0,x R}1B x ∈+，则A B 是（ ）A ．(1,2]-B ．[0,2]C ．{1,0,1,2}-D ．{0,1,2}2.【2013年湖北七市（州）高三年级联合考试理科数学】下列说法中不正确的个数是 （ ）①命题“∀x ∈R ，123+-x x ≤0”的否定是“∃0x ∈R ，12030+-x x >0”；②若“p ∧q ”为假命题，则p 、q 均为假命题；③“三个数a ，b ，c 成等比数列”是“b=ac ”的既不充分也不必要条件 A ．O B ．1 C ．2 D ．33.【湖北省黄冈市黄冈中学2013届高三下学期6月适应性考试数学理试题（B 卷）】已知集合{2,0,1}A =，集合{|||B x x a =<，且}x Z ∈，则满足A B ⊆的实数a 可以取的一个值是( )A ．0B ．1C ．2D ．34.【湖北省黄冈市黄冈中学2013届高三下学期6月适应性考试数学理试题（B 卷）】已知命题p ：,x R $?使1sin 2x x<成立． 则p Ø为（ ）A ．,x R "?1sin 2x x ³均成立 B ．,x R "?1sin 2x x <均成立 C ．,x R $?使1sin 2x x ³成立 D ．,x R $?使1sin 2x x =成立5.【湖北省荆门龙泉中学2014届高三年级8月月考数学（理科）试卷】下列有关命题的说法正确的是 ( ) A ．命题“若21x =，则1=x ”的否命题为：“若21x =，则1x ≠”．B ．“1x =-”是 “2560x x --=”的必要不充分条件．C ．命题“∃,R x ∈使得210x x ++<”的否定是：“对∀,R x ∈ 均有210x x ++<”．D ．命题“若x y =，则sin sin x y =”的逆否命题为真命题．【答案】D 【解析】试题分析：A 中，否命题应为若12≠x ，则1≠x ；B 中，1-=x ⇒2560x x --=，应为充分不必要条件；C 中，命题的否定应为：对∀,R x ∈ 均有012≥++x x ；Ｄ中，原命题为真，则逆否命题也为真.考点：命题的否定；四种命题．6.【湖北省荆门龙泉中学2014届高三年级8月月考数学（理科）试卷】钱大姐常说“便宜没好货”,她这句话的意思是:“不便宜”是“好货”的 （ ）条件. A ．充分 B ．必要 C ．充要 D ．既不充分也不必要7.【湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考理科数学】已知全集{}1,2,3,4,5,6,7,8,9U = 集合{}1,2,3,4,5,6A = 集合{}3,4,5,6,7,8B =，则集合U UAB 痧为（ ）A.{}3,4,5,6B.{}1,2,7,8,9C.{}1,2,3,4,5,6,7,8D.{}9【答案】D 【解析】试题分析：解法一：因为全集{}1,2,3,4,5,6,7,8,9U =，集合{}1,2,3,4,5,6A = 集合{}3,4,5,6,7,8B =，所以{}7,8,9U A =ð，{}1,2,9U B =ð，故{}9U UAB =痧，故选D ；解法二：因为全集{}1,2,3,4,5,6,7,8,9U =，集合{}1,2,3,4,5,6A = 集合{}3,4,5,6,7,8B =，所以{}1,2,3,4,5,6,7,8A B =，故(){}9U UU AB A B ==痧?，故选D.考点：1.集合的交集；2,.集合的补集运算8.【湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考理科数学】命题“对任意x R ∈都有21x ≥”的否定是（ ） A.对任意x R ∈，都有21x <B.不存在x R ∈，使得21x <C.存在0x R ∈，使得201x ≥ D.存在0x R ∈，使得201x <9.【湖北省重点中学2014届高三10月阶段性统一考试理科数学】已知全集U R =，设集合(){}ln 31A x y x ==-，集合(){}sin 2B y y x ==+，则()UA Bð为（ ）A.1,3⎛⎫+∞ ⎪⎝⎭ B.10,3⎛⎤ ⎥⎝⎦ C.11,3⎡⎤--⎢⎥⎣⎦D.∅考点：1.对数函数的定义域；2.三角函数的值域；3.集合的补集与交集运算10.【湖北省重点中学2014届高三10月阶段性统一考试理科数学】已知命题:p x R ∃∈，2lg x x ->，命题:q x R ∀∈，sin x x <，则 （ ）A.命题p q ∨是假命题B.命题p q ∧是真命题 C.命题()p q ⌝∧是真命题 D.命题()p q ⌝∨是假命题11.【湖北省重点中学2014届高三10月阶段性统一考试理科数学】在ABC ∆中，“()()sin cos cos sin 1A B B A B B -+-≥”是 “ABC ∆是直角三角形”的（ ）A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件不必要条件，故选A.考点：1.两角和的正弦公式；2.充分必要条件12.【湖北孝感高中2014届高三年级九月调研考试数学（理）】已知全集U R =，集合{}021x A x =<<，{}3log0B x x =>，则()U A C B =（ ）A ． {}1x x >B ．{}0x x >C ．{}01x x <<D ．{}0x x <13.【湖北孝感高中2014届高三年级九月调研考试数学（理）】已知命题p ：020,log 1x R x +∃∈=，则p ⌝是（ ）A ．*2,log 1x R x ∀∈≠ B ．*2,log 1x R x ∀∉≠C ．*020,log 1x R x ∃∈≠D ．*020,log 1x R x ∃∉≠14.【湖北孝感高中2014届高三年级九月调研考试数学（理）】满足{}1234M a a a a ⊆，，，，且{}{}12312Ma a a a a =，，，的集合M 的个数是（ ）A ．1B ．2C ．3D ．415.【湖北孝感高中2014届高三年级九月调研考试数学（理）】“0a b >>”是“222a b ab +<”的 （ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件16.【湖北稳派教育2014届高三10月联合调研考试数学理科试题】已知集合}1|{-==x y x A ，}1001,lg |{≤≤==x x y x B ，则=B A （ ） A. ]100,1[ B.]2,1[ C. ]2,0[ D. )10,0[ 【答案】B【解析】试题分析：依题意[1,)A =+∞，[0,2]B =，∴[1,2]A B =，故选B.考点：函数的定义域，值域，交集.17.【2013届高中毕业生四月调研理科数学测试题】命题“若220x y +=，则0x y ==”的否命题是（ ）A. 若220x y +=，则 x 、y 中至少有一个不为0B. 若220x y +≠，则 x 、y 中至少有一个不为0 C. 若220x y +≠，则 x 、y 都不为0 D. 若220x y +=，则 x 、y 都不为018.【湖北省教学合作2014届高三10月联考数学试题理科数学】不等式组|21|32113x x x -<⎧⎪+⎨≤⎪-⎩的解集为.二．能力题组1. 【湖北省教学合作2014届高三10月联考数学试题理科数学】下列给出的四个命题中，说法正确的是（ ）A ．命题“若21x =，则1x =”的否命题是“若21x =，则1x ≠”； B ．“1x =-”是“2560x x --=”的必要不充分条件；C ．命题“存在x R ∈，使得210x x ++<”的否定是“对任意x R ∈，均有210x x ++<”； D ．命题“若x y =，则sin sin x y =”的逆否命题为真.2.【湖北稳派教育2014届高三10月联合调研考试数学理科试题】给出下列命题：①命题“01R 2>++∈∀x x x ，的否定是：01R,2<=+∈∃x x x ； ②命题“若0=ab ，则0=a 或0=b ”的否命题是“若0≠ab ，则0≠a 且0≠b ”；③x ∃、R ∈y ，y x y x sin sin )sin(-=-；④向量，均是单位向量，其夹角为θ，则命题“1|:|>-b a p ”是命题“]65,2[:ππθ∈q ”的充要条件.其中正确的命题的个数是（ ）A. 4B. 3C.2D.1 【答案】C 【解析】试题分析：R ∈∀x ，012>++x x 的否定应为R ∈∃x ，012≤++x x ，故①错；②正确；③正确；21cos 21121)(1:222<⇒<⋅⇒>+-⇒>-⇒>-θb a b b a a b a b a p ],3(ππθ∈⇒，从而⇒∈)65,2[:ππθq 1:>-b a p ，反之不成立，故④错．考点：全程命题，特称命题，充要条件.3.【湖北稳派教育2014届高三10月联合调研考试数学理科试题】在整数集Z 中，被5整除所得余数为k 的所有整数组成一个“类”，记为}Z |5{][∈+=n k n k ，4,3,2,1,0=k ，给出如下三个结论： ①]4[2014∈； ②]2[2∈-；③]4[]3[]2[]1[]0[Z =；、④“整数a 、b 属于同一“类”的充要条件是“]0[∈-b a ”.其中，正确结论的个数是（ ）A. 0B. 1C. 2D. 34.【湖北省荆门龙泉中学2014届高三年级8月月考数学（理科）试卷】已知22{||4},{1(41)2}A x x aB x og x x =-<=-->（1）若a =l ，求 A B ；（2）若AB R =，求实数a 的取值范围． 【答案】(1)AB ={}13|-<<-x x ;(2) .31<<a【解析】 试题分析：（１）把a ＝１代入Ａ和Ｂ，解不等式，再取交集即可.（２）把Ａ和Ｂ先解出来，然后再取A B R =，从而求出.试题解析：(1)当1=a 时，Ａ＝{},53|<<-x x Ｂ＝{}.51|>-<x x x 或∴{};13|<<-=⋂x x B A（２）{},44|+<<-=a x a x A {}.51|>-<=x x x B 或且R B A =⋃，∴.31<<a 考点：1、不等式的解法；２、集合的关系及运算.5.【湖北省重点中学2014届高三10月阶段性统一考试理科数学】已知():sin cos r x x x m+>；()2:10s x x mx ++>，如果x R ∀∈，()r x 与()s x 有且仅有一个是真命题，求实数m 的取值范围.6.【湖北孝感高中2014届高三年级九月调研考试数学（理）】已知命题p：不等式11x m->-的解集为R，命题q：()()52=-xf x m是(,)-∞+∞上的增函数，若p或q为真命题，p且q为假命题，求实数m的取值范围．7.【湖北稳派教育2014届高三10月联合调研考试数学理科试题】已知命题]2,1[:∈∀x p ，02≥-a x ，命题R :0∈∃x q ，使得01)1(020<+-+x a x .若“p 或q 为真”，“p 且q 为假”，求实数a 的取值范围.【答案】3>a 或11≤≤-a .【解析】试题分析：有条件求出命题p 、q 为真的a 的取值范围，再由p 或q 为真，p 且q 为假， 则p 与q 一真一假，分两种情况求出结论.试题解析：由条件知，2x a ≤对]2,1[∈∀x 成立，∴1≤a ；∵R 0∈∃x ，使得01)1(020<+-+x a x 成立. ∴不等式01)1(020<+-+x a x 有解，∴04)1(2>--=∆a ，解得3>a 或1-<a ；（6分） ∵p 或q 为真，p 且q 为假，∴p 与q 一真一假．①p 真q 假时，11≤≤-a ；②p 假q 真时，3>a .∴实数a 的取值范围是3>a 或11≤≤-a . （12分） 考点：复合命题的真假，函数三．拔高题组1.【湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考理科数学】已知命题:p 方程2220a x ax +-=在[]1,1-上有解，命题:q 函数()22f x x ax =+2a +的值域为[)0,+∞，若命题“p 或q ”是假命题，求实数a 的取值范围.2.【湖北孝感高中2014届高三年级九月调研考试数学（理）】已知}04|{2=+=x x x A , }01)1(2|{22=-+++=a x a x x B ，其中a R ∈，如果A∩B=B，求实数a 的取值范围．⑴当B =∅时，224(1)4(1)0a a ∆=+--<，解得1a <-； …………5分。

一．基础题组1. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】若集合{23},{14}A x x B x x x =-≤≤=<->或，则集合A B = ．2. 【南京市、盐城市2014届高三第一次模拟考试】“p q ∨为真命题”是“p ⌝为假命题”成立的 条件．3. 【江苏省诚贤中学2014届高三数学月考试题】已知集合{}(1)0P x x x =-≥，Q ={})1ln(|-=x y x ，则P Q = ．4. 【南京市、盐城市2014届高三第一次模拟考试】已知集合{3,1,1,2}A =--，集合[0,)B =+∞，则______A B = .5. 【江苏省扬州中学2013—2014学年第一学期月考】已知集合⎭⎬⎫⎩⎨⎧∈==R x y y A x ,21|，{}R x x y y B ∈-==),1(log |2，则=⋂B A ．6. 【苏州市2014届高三调研测试】已知集合A = { x | x < 2 }，B = { -1，0，2，3 }，则A∩B = ▲ ．7. 【江苏省兴化市安丰高级中学2014届高三12月月考】设集合{}4,3,2,1=U ，{}2,1=A ,{}4,2=B ,则U AB = （）ð ．8. 【江苏省扬州中学2013—2014学年第一学期月考】已知命题:p “若=，则||||=”，则命题p 及其逆命题、否命题、逆否命题中，正确命题的个数是 ．二．能力题组1. 【江苏省诚贤中学2014届高三数学月考试题】由命题“02,2≤++∈∃m x x R x ”是假命题，求得实数m 的取值范围是),(+∞a ，则实数a 的值是 ．2. 【南京市、盐城市2014届高三第一次模拟考试】设函数()cos(2)f x x ϕ=+，则“()f x 为奇函数”是“2πϕ=”的 条件.（选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”）3. 【江苏省通州高级中学2013-2014学年度秋学期期中考试】已知集合A ＝{x ｜x ＞2，或x ＜－1}，B ＝{x ｜a x b ≤≤}，若A B R = ，A B ={x ｜24x <≤}，则ba＝_ ▲__ .【答案】-4 【解析】试题分析：由{}{}|x 2x 1,|2<x 4A x A B R A B x =><-==≤ 或,可得{}|14B x x =-≤≤ ,则1,4a b =-= ,故4ba=-. 考点：集合的运算4. 【苏北四市2014届高三第一次质量检测】已知集合{2}A a =+，{1,1,3}B =-，且A B ⊆，则实数a 的值是 ．5.【江苏省兴化市安丰高级中学2014届高三12月月考】 已知命题：“{}|11x x x ∃∈-<<，使等式20x x m --=成立”是真命题． （1）求实数m 的取值集合M ；（2）设不等式()(2)0x a x a -+-<的解集为N ，若x N ∈是x M ∈的必要条件，求a 的取值范围．试题解析：(1) 由题意知，方程20x x m --=在()1,1-上有解，即m 的取值范围就为函数x x y -=2在()1,1-上的值域，易得124M m m ⎧⎫=-≤<⎨⎬⎩⎭(2) 因为x N ∈是x M ∈的必要条件，所以N M ⊆当1=a 时，解集N 为空集，不满足题意当1>a 时，a a ->2，此时集合{}a x a x N <<-=2|则⎪⎩⎪⎨⎧≥-<-2412a a ，解得49>a当1<a 时，a a -<2，此时集合{}a x a x N -<<=2|。