应用光学第二章例题

10．一个双凸透镜，两面的曲率半径为r1=15cm, r2=10cm, 透镜玻璃的折射系数n=1.5,透镜厚度d=3cm, 透镜置于空气中，求透镜的主焦点及主平面的位置。

11．凸透镜焦距为10厘米，凹透镜焦距为4厘米，两个透镜相距12厘米，已知物在凸透镜左方20厘米处，计算像的位置和横向放大率。

12．空气中双凹厚透镜的两个凹面半径r1和r2分别为-8厘米和7厘米，沿主轴的厚度为2厘米，玻璃折射率n为1.5。

求焦点和主平面的位置。

13．已知两透镜的像方焦距分别为5厘米和10厘米，两镜光学间隔为10厘米，物离透镜为15厘米，用复合光组法求最后的像的位置。

14．一焦距为20厘米的薄透镜与一焦距为20厘米的薄凹透镜相距6厘米，求（1）复合光组焦点及主平面的位置。

（2）若物放在凸透镜前30厘米处，求像的位置和放大率。

第二章 例 题例题2.1 凸平透镜r 1=100mm ，r 2=∞，d=300mm ，n=1.5，当物体在-∞时候，1）求高斯像面的位置；2）在平面上刻十字，问其共轭像在什么位置；3）当入射高度为h=10mm ，问光线的像方截距是多少？和高斯像面相较相差多少？说明什么问题？解：1）依照近轴光线光路计算公式能够求出高斯像面的位置。

将1111,' 1.5,1,100l n n r mm =-∞===代入单个折射球面成像公式'''n n n n l l r--=，能够求得1'300l mm =。

又由题意d=300mm ，发觉现在所成的像在凸平透镜的第二面上。

2）由光路可逆原理明白，假设在平面上刻十字，其共轭像应在物方-∞处。

3）当入射高度为h=10mm 时，光路如以下图所示：现在利用物在无穷远时，L =−∞时，公式sin sin 'sin '''sin ''(1)sin 'h I r n I I n U U I I I L r U ⎧=⎪⎪⎪=⎪⎨⎪=+-⎪⎪=+⎪⎩中的第一和第四式求解得： ※ 光线通过第一面折射时，11110sin 0.1100h I r ===，因此1 5.739o I =。

又11111sin 'sin 0.10.06667' 1.5n I I n ==⨯=，因此1'arcsin0.06667 3.822o I ==，1111''(0 5.739 3.822) 1.9172o oU U I I =+-=+-=，1111sin '0.0667'11001299.374sin '0.0334547I L r mm U ⎛⎫⎛⎫=⨯+=⨯+= ⎪ ⎪⎝⎭⎝⎭。

※ 光线再通过第二个面折射，21'0.626L L d mm =-=-，21' 1.9172o I U -==，那么2222sin 'sin 1.5sin1.91720.05018'o n I I n ==-=-，2' 2.87647o I =-。

应用光学试题第二章一、填空题（建议每空1分）（请同学们不要写错别字，数字不要用大写，术语要标准，否则按错处理，不要用科学记数法如4101⨯）I 级I 级1空1、 焦点又称为后焦点或第二焦点。

像方2、过像方焦点'F 作一垂直于光轴的平面即为 焦平面。

像方3、像方焦点'F 是像方焦平面上的一个特殊点，该点对应的是物方孔径角=u 度的一束平行于光轴的平行光。

4、从物方焦点F 发出的光经过系统后均为平行于 的光。

光轴5、过 作垂直于光轴的平面称为物方焦平面。

物方焦点6、垂轴放大率为=β 倍的这对共轭平面为主平面（简称主面）。

17、主平面与光轴的交点称为 。

主点8、像方主平面与 的交点称为像方主点'H 。

光轴9、焦距属于沿轴线段，以各自的 为原点判断其符号。

主点10、 焦距可表示式为tguh 。

物方11、光学系统的 可以看作是焦距的另外一种表示形式， 光焦度12、 是指角放大率1+=γ的一对共轭点。

节点13、经过物方节点的光线其共轭光线经过 节点。

像方14、 法主要是应用光学系统基点和基面的性质，通过选用适当的光线或辅助线画出其共轭光线的方法。

图解15、牛顿公式是以各自的为原点确定物、像的具体位置。

焦点16、高斯公式是以为原点来描述物、像的具体位置。

主点17、将一个正单透镜与一个负单透镜进行胶合，称之为透镜。

双胶合18、望远系统是最典型的光学系统，其系统焦点位于无穷远处，焦距为无限大。

无焦19、望远系统的光学间隔=∆。

20、是由两个折射面包围的一种透明介质构成的光学元件，折射面可以是球面、平面或非球面。

透镜21、是指当透镜的厚度与焦距或曲率半径相比是一个很小的数值时，厚度d可忽略不计的透镜。

薄透镜22、透镜主平面与之间的距离为焦距。

焦点23、透镜物与像之间的距离称为。

共轭距24、筒长L是指第一个光组到之间的距离。

像面（或像平面）25、是指系统最后一面到像平面之间的距离。

后工作距离26、按照透镜形状的不同，正透镜又可分为透镜、平凸透镜及月凸透镜，双凸27、负透镜又分为透镜、平凹透镜及月凹透镜，其特征是中心厚度比边缘厚度薄。

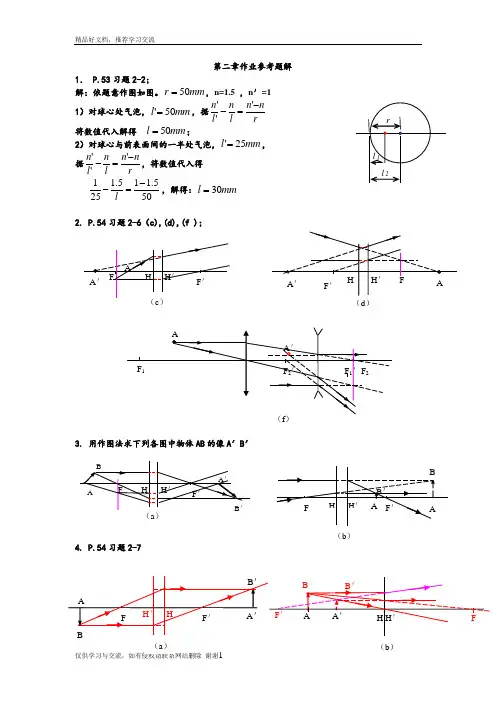
《应用光学》第二版胡玉禧第二章作业参考题解-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII第二章作业参考题解1． P.53习题2-2；解：依题意作图如图。

mm r 50=，n=1.5 ，n ＇=11）对球心处气泡，mm l 50'=，据rnn l n l n -=-'''将数值代入解得 mm l 50=；2）对球心与前表面间的一半处气泡，mm l 25'=， 据rn n l n l n -=-'''，将数值代入得 505.115.1251-=-l ，解得：mm l 30=2. P.54习题2-6（c),(d),(f )；3. 用作图法求下列各图中物体AB 的像A ′B ′4. P.54习题2-7l 1 l 2rAH H ′ F ′ （cA ′ FFH H ′ （dF ′AA ′F 1（fF 2′ A A ′ F 1′F 2B FA H H ′ F ′（a A ′B ′ AB H H ′ （bF F ′ABFAB H H ′ F ′ A B A B H ′ H F F ′ A B5. P.55习题2-10 解： 据题意有2111-=-=x f β （1） 122-=-=x f β （2） 10012+=x x （3） 联立（1）（2）（3）式解得 )(100mm f -=； 或据 ''f x -=β 和题目条件可以解得 )(100'mm f = （说明：本题也可以用高斯公式求解） 6. P.55习题2-13解：由于两透镜密接，故d = 0 ， 所求 ''x f f x L ++--= ，或 'l l L +-= 把透镜看成光组，则此为双光组组合问题。

可由∆-='''21f f f 和∆=21f f f 计算组合后系统的焦距：)(31005010050100'''21mm f f f =+⨯-=∆-= ，)(310050100)50(10021mm f f f -=---⨯-=∆= 又 （法一）101''-=-=-=x f f x β， 所以 )(310'101'mm f x =-= ，)(3100010mm f x -== )(3.403312103103100310031000''mm x f f x L ≈=+++=++--=又 （法二）101'-==l l β， 所以 '10l l -= ，代入高斯公式得1003'1011=--'l l 解得 )(311031001011'mm l =⨯=， )(31100'10mm l l -=-=所以 )(3.40331210311031100'mm l l L ≈=+=+-= 7. P.55习题2-18 解：据题意透镜为同心透镜，而r 1=50mm ，d =10 mm ，故有 r 2= r 1-d = 40 mm ，所以，由dn r r n dr l H )1()(121-+--=得)(50163.5163.1550010)15163.1()5040(5163.15010mm l H =+--=⨯-+-⨯-=dn r r n dr l H )1()('122-+--=得)(40163.5163.1540010)15163.1()5040(5163.14010'mm l H =+--=⨯-+-⨯-=10)15163.1()5040(5163.1)15163.1(40505163.1)1()()1('221221⨯-+-⨯-⨯⨯=-=-+--=f d n r r n n r nr f)(37168.587163.56.3032665656.2828656.76.3032mm -=-=+-=。

第二章 例 题例题2.1 凸平透镜r 1=100mm ，r 2=∞，d=300mm ，n=1.5，当物体在-∞时候，1）求高斯像面的位置；2）在平面上刻十字，问其共轭像在什么位置；3）当入射高度为h=10mm ，问光线的像方截距是多少？和高斯像面相比相差多少？说明什么问题？解：1）根据近轴光线光路计算公式可以求出高斯像面的位置。

将1111,' 1.5,1,100l n n r mm =-∞===代入单个折射球面成像公式'''n n n n l l r--=，可以求得1'300l mm =。

又由题意d=300mm ，发现此时所成的像在凸平透镜的第二面上。

2）由光路可逆原理知道，若在平面上刻十字，其共轭像应在物方 -∞处。

3）当入射高度为h=10mm 时，光路如下图所示：此时利用物在无限远时，L =−∞时， 公式sin sin 'sin '''sin ''(1)sin 'h I r n I I n U U I I I L r U ⎧=⎪⎪⎪=⎪⎨⎪=+-⎪⎪=+⎪⎩中的第一和第四式求解得： ※ 光线经过第一面折射时，11110sin 0.1100h I r ===，所以1 5.739o I =。

又11111sin 'sin 0.10.06667' 1.5n I I n ==⨯=，所以1'arcsin 0.06667 3.822o I ==，1111''(0 5.739 3.822) 1.9172o o U U I I =+-=+-=，1111sin '0.0667'11001299.374sin '0.0334547I L r mm U ⎛⎫⎛⎫=⨯+=⨯+= ⎪ ⎪⎝⎭⎝⎭。

※ 光线再经过第二个面折射，21'0.626L L d mm =-=-，21' 1.9172o I U -==，则2222sin 'sin 1.5sin1.91720.05018'o n I I n ==-=-，2' 2.87647o I =-。

第二章作业参考题解1． P.53习题2-2；解：依题意作图如图。

mm r 50=，n=1.5 ，n ＇=1 1）对球心处气泡，mm l 50'=，据rnn l n l n -=-''' 将数值代入解得 mm l 50=；2）对球心与前表面间的一半处气泡，mm l 25'=，据rn n l n l n -=-'''，将数值代入得 505.115.1251-=-l ，解得：mm l 30=2. P.54习题2-6（c),(d),(f )；3. 用作图法求下列各图中物体AB 的像A ′B ′4. P.54习题2-7l 1 l 2rAH H ′F ′ （c ） A ′ F FH H ′ （d ）F ′AA ′F 1 （f ）F 2′AA ′ F 1′F 2B F AH H ′ F ′ （a ）A ′B ′ A ＇ B ＇H H ′ （b ）FF ′ ABFA ＇B ＇ H H ′ F ′ABA ＇B ＇H ′ H （a ）F F ′ A B5. P.55习题2-10 解： 据题意有2111-=-=x f β （1） 122-=-=x f β （2） 10012+=x x （3） 联立（1）（2）（3）式解得 )(100mm f -=； 或据 ''f x -=β 和题目条件可以解得 )(100'mm f = （说明：本题也可以用高斯公式求解） 6. P.55习题2-13解：由于两透镜密接，故d = 0 ， 所求 ''x f f x L ++--= ，或 'l l L +-=把透镜看成光组，则此为双光组组合问题。

可由∆-='''21f f f 和∆=21f f f 计算组合后系统的焦距：)(31005010050100'''21mm f f f =+⨯-=∆-= ，)(310050100)50(10021mm f f f -=---⨯-=∆= 又 （法一）101''-=-=-=x f f x β， 所以 )(310'101'mm f x =-= ，)(3100010mm f x -== )(3.403312103103100310031000''mm x f f x L ≈=+++=++--=又 （法二）101'-==l l β， 所以 '10l l -= ，代入高斯公式得 1003'1011=--'l l 解得 )(311031001011'mm l =⨯=， )(31100'10mm l l -=-=所以 )(3.40331210311031100'mm l l L ≈=+=+-=7. P.55习题2-18解：据题意透镜为同心透镜，而r 1=50mm ，d =10 mm ，故有 r 2= r 1-d = 40 mm ，所以，由dn r r n dr l H )1()(121-+--=得)(50163.5163.1550010)15163.1()5040(5163.15010mm l H =+--=⨯-+-⨯-=dn r r n dr l H )1()('122-+--=得)(40163.5163.1540010)15163.1()5040(5163.14010'mm l H =+--=⨯-+-⨯-=10)15163.1()5040(5163.1)15163.1(40505163.1)1()()1('221221⨯-+-⨯-⨯⨯=-=-+--=f d n r r n n r nr f)(37168.587163.56.3032665656.2828656.76.3032mm -=-=+-=绿叶对根的情意——学会与父母沟通【教学对象】初中二年级【教学时间】一节课，40分钟 【教学理念分析】人际交往和沟通是个体社会和人格发展成熟的重要标志。

第二章一、选择题1、关于全反射现象，下列说法正确的是( )A．光线由光疏介质向光密介质传播时可能发生全反射B．光线由光密介质向光疏介质传播时可能发生全反射C．光线由光疏介质向光密介质传播时一定发生全反射D．光线由光密介质向光疏介质传播时一定发生全反射答案：B2、下列能成完善像的光学系统是（）A．平面折射系统B．平面反射系统C．球面折射系统D．球面反射系统答案：B3、若物位于凹面反射镜的焦点和曲率中心之间，则下列说法正确的是（）A．成倒立放大实像B．成倒立缩小实像C．成正立放大虚像D．成倒立缩小虚像答案：A4、关于棱镜片下列说法正确的是（）A．改变光线方向，不改变光束的聚散度B．不改变光线方向，改变光束的聚散度C．光线方向和光束的聚散度都改变D．光线方向和光束的聚散度都不改变答案：A5、实物通过平面反射镜所成的像为（）A．实像B．虚像C．实像和虚像均有可能D．实像和虚像重叠答案：B6、若物位于凹面反射镜的焦点和顶点之间，则下列说法正确的是（）A．成倒立缩小实像B．成倒立放大实像C．成倒立缩小虚像D．成正立放大虚像答案：D7、平面反射光学系统的横向放大率( )A．小于1B．大于1C．等于1D．以上都不对答案：D8、对于单球面近轴折射成像系统,若凹面侧的折射率大于凸面侧的折射率，下列说法正确的是（）A．该系统为发散型B．该系统为会聚型C．是发散型还是会聚型与物点的位置有关D．是发散型还是会聚型与像点的位置有关正确答案：B9、关于球面折射光学系统成像，下列说法正确的是（）A．能成完善的像B．不能成完善的像C．能否成完善像要依据条件而定D．部分成完善的像正确答案：B10、两个节点是一对（）A．角放大率为+1的共轭点B．角放大率为-1的共轭点C．角放大率>1的共轭点D．角放大率正确答案：A11、关于理想光学系统,下列说法正确的是（）A．主平面是横向放大率大于1的一对共轭面B．主平面是横向放大率小于1的一对共轭面C．主平面是横向放大率为-1的一对共轭面D．主平面是横向放大率为+1的一对共轭面正确答案：D二、简答题12、简述折射定律；13、简述反射定律；第三章1、人眼的瞳孔相当于（）A．入瞳B．出瞳C．孔径光阑D．透镜答案：C2、当物点在垂直光轴方向上下移动时，系统的孔径光阑（）A．增大B．减小C．不变D．无法判断答案：C3、以下关于景深和焦深的描述，错误的是（）A．景深是能在像平面上获得清晰像的物空间深度B．焦深是能成清晰像的像空间深度C．眼的分辨率越大，景深越小D．焦深增大，眼的分辨率就增大答案：B4、视场光阑经它前面的光学系统所成的像为（）A．入瞳B．出瞳C．入射窗D．出射窗答案：C5、大多数望远镜和显微镜的孔径光阑都位于（）A．物镜B．目镜C．物镜和目镜之间D．无法判断答案：A6、视场光阑所限制的成像物体的实际大小称为（）A．物方视场B．像方视场C．物方视场角D．像方视场角答案：A7、光学系统中的孔径光阑和视场光阑的关系是（）A．孔径光阑可作为视场光阑B．视场光阑也作为孔径光阑C．孔径光阑一般就是视场光阑D．孔径光阑和视场光阑两者不能合一答案：D8、以下关于主光线的描述，错误的是（）A．通过入瞳中心B．通过出瞳中心C．通过孔径光阑中心D．通过光学系统的节点答案：D9、摄影时，有的摄像师会在镜头前面挂上窗纱，其主要作用是（）A．减少光线通过B．增加图像清晰度C．增加景深D．减小景深答案：C10、瞳孔缩小的时候（）A．景深增加B．景深减小C．焦距增加D．焦距减小答案：A二、简答题11、简述什么是入射光瞳和出射光瞳孔；12、简述什么是景深和焦深；第四章一、选择题1、球差与下面那项因素有关（）A．孔径角B．视场大小C．物距D．离轴距离答案：A2、如图，是轴外点以宽光束经过光学系统成像时产生的像差，该像差是（）A．球差B．慧差C．场区D．色差答案：B3、如图，物面上轴外区域中的一个很小的“十”字图案经过光学系统成像后，在子午像面和弧矢像面分别在不同方向上成清晰的像，其中在子午面内，“十”字线的哪个方向成像清晰（）A．水平方向B．垂直方向C．任何方向D．主轴方向答案：A4、以下哪个是枕型畸变（）A． B． C． D．答案：A5、以下哪个是桶型畸变（）A． B． C． D．答案：B6、缩小光学系统的孔径光阑，哪些像差会得到改善（）A．球差、像散B．像散、场曲C．球差、彗差D．彗差、畸变答案：C7、如图，轴上点以宽光束成像时产生的像差为（）A．球差B．慧差C．场区D．色差答案：A8、轴外点以宽光束经过光学系统成像时，会产生慧差，慧差包括（）A．子午慧差和垂轴慧差B．弧矢慧差和纵向慧差C．弧矢慧差和子午慧差D．垂轴慧差和纵向慧差答案：C9、如图，物面上轴外区域中的一个很小的“十”字图案经过光学系统成像后，在子午像面和弧矢像面分别在不同方向上成清晰的像，造成这种现象的原因是（）A．像散B．场曲C．畸变D．色差答案：B10、单球面折射镜有几对无球差的共轭点（）A．1对B．2对C．3对D．以上选项都不对答案：C11、在7种几何像差中，不影响成像清晰度的有几种（）A．1种B．2种C．3种D．以上选项都不对答案：B12、在7种几何像差中，对轴上点成像产生圆形弥散斑的有几种（）A．1种B．2种C．3种D．以上选项都不对答案：B二、简答题13、简述什么是场曲；14、简述什么是位置色差；第五章一、选择题1、在均匀透明介质中，如果不考虑光能损失，则位于同一条光线上的各点，在光线进行的方向上光亮度（）A．不变B．变强C．变弱D．以上都不对答案：A2、在理想成像时，由物点A 发出的光线均通过像点A '，因此物和像的光亮度B 和B '之间的关系为( )A ．3B B n n '⎛⎫'= ⎪⎝⎭B ．3B B n n ⎛⎫'= ⎪'⎝⎭C ．2B B n n '⎛⎫'= ⎪⎝⎭D ．2B B n n ⎛⎫'= ⎪'⎝⎭ 答案：C3、下列说法正确的是( )A ．光照度定义为单位面积上所接受的辐射强度的大小B ．光照度的单位是流明(lm )C ．1lx 等于21m 面积上发出或接收1lm 的光通量D ．光亮度的单位是勒克斯(lx )答案：C4、颜色有三种特性，其中不包括（ ）A ．明度B ．色调C ．彩度D ．色温答案：D5、假定在折射率为1n 的介质内，入射光束的光亮度为1B ；在折射率为2n 的介质内，假设折射光束的光亮度为2B ，则（ ）A ．212221B B n n =B ．222211B B n n =C ．1221B B n n = D ．2211B B n n =答案：B6、在实际光学系统中，当物像空间介质相同时，下列说法正确的是（）A．像的光亮度永远等于物的光亮度B．像的光亮度可能等于物的光亮度，视具体情况C．像的光亮度永远大于物的光亮度D．像的光亮度永远小于物的光亮度答案：D7、以下叙述正确的是（）A．光通量的单位是cd，发光强度的单位是lm，光照度的单位是nt，光亮度的单位是lx B．光通量的单位是lm，发光强度的单位是cd，光照度的单位是lx，光亮度的单位是nt C．光通量的单位是lx，发光强度的单位是cd，光照度的单位是lm，光亮度的单位是nt D．光通量的单位是lm，发光强度的单位是nt，光照度的单位是lx，光亮度的单位是cd 答案：B8、彩色的纯洁性称为（）A．饱和度B．纯度C．明度D．色度答案：A9、人眼只能对可见光产生视觉，下列说法正确的是（）A．对黄绿光最不敏感B．对红光和紫光较好C．对红外光全无视觉反应D．对紫外光有视觉反应答案：C10、下列说法正确的是（）A．从能量的观点看，光线从光源(发光体)发出，经过中间介质(如大气等)和光学系统，最后到达接收器(如人眼、感光底片、光电元件等)是一个能量传输过程B．研究可见光的测试、计量和计算的学科称为“辐射度学”C．研究X光、紫外光、红外光以及其他电磁波辐射的测试、计量和计算的学科称为“光度学”D．光度学是辐射量度学的一部分或特例，光度学中的光是指全波段光答案：A二、简答题11、简述什么是朗伯定律；12、简述什么是光通量并写出表达式。

1．一物体在曲率半径12厘米的凹面镜的顶点左方4厘米处，求像的位置及横向放大率，并作出光路图。

2．一直径为4厘米的长玻璃棒，折射率为1.5，其一端磨成曲率半径为2厘米的半球形。

长为0.1 厘米的物垂直置于棒轴上离棒的凹面顶点8厘米处。

求像的位置及大小。

并作出光路图。

3．一玻璃半球的曲率半径为R，折射率为1.5，其平面的一边镀银。

一物高为h，放在曲面顶点2R处，求（1）由曲面所组成的第一个像的位置。

（2）这一光具所组成的最后的像在那里？4．证明：光线相继经过几个平行分界面的多层介质时，出射光线的方向只与入射方向及两边的折射率有关，与中间各层介质无关。

第二章作业：1、一个玻璃球直径为400mm，玻璃折射率为1.5。

球中有两个小气泡，一个在球心，一个在1/2半径处。

沿两气泡连线方向，在球的两侧观察这两个气泡，它们应在什么位置？如在水中观察(水的折射率为1.33)时，它们又应在什么位置？答案：空气中：80mm、200mm；400mm、200mm水中：93.99mm、200mm；320.48mm、200mm3、一个玻璃球直径为60mm，玻璃折射率为1.5，一束平行光射到玻璃球上，其汇聚点在何处？答案：l'=15mm4、一玻璃棒(n=1.5)，长500mm，两端面为凸的半球面，半径分别为r1=50mm, r2= -100mm，两球心位于玻璃棒的中心轴线上。

一箭头高y=1mm，垂直位于左端球面顶点之前200mm处，垂直于玻璃棒轴线。

试画出结构简图，并求a)箭头经玻璃棒成像在什么位置(l2')？b)整个玻璃棒的垂轴放大率为多少？答案：l2'= -400mm、-3第三章作业：1、已知一个透镜把物体放大-3⨯，当透镜向物体移近18mm时，物体将被放大-4⨯，试求透镜的焦距。

答案：216mm2、一个薄透镜对某一物体成实像，放大率为-1⨯。

以另一薄透镜紧贴此薄透镜，则见像向透镜方向移动了20mm，放大率为原来的3/4，求两薄透镜的焦距。

答案：40mm、240mm3、一束平行光入射到平凸透镜上，汇聚于透镜后480mm处。

如在此透镜凸面上镀反射膜，则平行光汇聚于透镜前80mm处，求透镜折射率和凸面曲率半径。

答案：1.5、-240mm5、一块厚透镜，n=1.6，r1=120mm，r2=-320mm，d=30mm，试求该透镜的焦距及基点位置。

如果物距l1= -5m，像在何处？如果平行光入射时，使透镜绕一和光轴垂直的轴转动，而要求像点位置不变，问该轴安装在何处？答案：f'=149.27mm、l F'=135.28mm、l F= -144.02mm、l H'= -13.99mm、l H=5.25mm l2'=139.87mm像方节点，即像方主点6、由两薄透镜组成的对无穷远物成像的短焦距物镜，已知其焦距为35mm，筒长T=65mm，后工作距为50mm，求系统结构。

应用光学试题第二章一、填空题（建议每空1分）（请同学们不要写错别字，数字不要用大写，术语要标准，否则按错处理，不要用科学记数法如4101⨯）I 级I 级1空1、 焦点又称为后焦点或第二焦点。

像方2、过像方焦点'F 作一垂直于光轴的平面即为 焦平面。

像方3、像方焦点'F 是像方焦平面上的一个特殊点，该点对应的是物方孔径角=u 度的一束平行于光轴的平行光。

4、从物方焦点F 发出的光经过系统后均为平行于 的光。

光轴5、过 作垂直于光轴的平面称为物方焦平面。

物方焦点6、垂轴放大率为=β 倍的这对共轭平面为主平面（简称主面）。

17、主平面与光轴的交点称为 。

主点8、像方主平面与 的交点称为像方主点'H 。

光轴9、焦距属于沿轴线段，以各自的 为原点判断其符号。

主点10、 焦距可表示式为tguh 。

物方11、光学系统的 可以看作是焦距的另外一种表示形式， 光焦度12、 是指角放大率1+=γ的一对共轭点。

节点13、经过物方节点的光线其共轭光线经过 节点。

像方14、 法主要是应用光学系统基点和基面的性质，通过选用适当的光线或辅助线画出其共轭光线的方法。

图解15、牛顿公式是以各自的为原点确定物、像的具体位置。

焦点16、高斯公式是以为原点来描述物、像的具体位置。

主点17、将一个正单透镜与一个负单透镜进行胶合，称之为透镜。

双胶合18、望远系统是最典型的光学系统，其系统焦点位于无穷远处，焦距为无限大。

无焦19、望远系统的光学间隔=∆。

20、是由两个折射面包围的一种透明介质构成的光学元件，折射面可以是球面、平面或非球面。

透镜21、是指当透镜的厚度与焦距或曲率半径相比是一个很小的数值时，厚度d可忽略不计的透镜。

薄透镜22、透镜主平面与之间的距离为焦距。

焦点23、透镜物与像之间的距离称为。

共轭距24、筒长L是指第一个光组到之间的距离。

像面（或像平面）25、是指系统最后一面到像平面之间的距离。

后工作距离26、按照透镜形状的不同，正透镜又可分为透镜、平凸透镜及月凸透镜，双凸27、负透镜又分为透镜、平凹透镜及月凹透镜，其特征是中心厚度比边缘厚度薄。

l -----------2si n22-2.如图所示，两相干平面光波的传播方向与干涉场法线的夹角分别为0和R，试求干涉场上的干涉条纹间距。

2-3.在杨氏实验装置中，两小孔的间距为0.5mm，光屏离小孔的距离为50cm。

当以折射率为1.60的透明薄片贴住小孔S2时，发现屏上的条纹移动了1cm，试确定该薄片的厚度。

2-4.在双缝实验中，缝间距为0.45mm，观察屏离缝115cm，现用读数显微镜测得10个条纹（准确地说是11个亮纹或暗纹）之间的距离为15mm，试求所用波长。

用白光实验时，干涉条纹有什么变化？2-5. 一波长为0.55 m的绿光入射到间距为0.2mm的双缝上，求离双缝2m远处的观察屏上干涉条纹的间距。

若双缝距离增加到2mm，条纹间距又是多少?2-6.波长为0.40 m〜0.76 m的可见光正入射在一块厚度为 1.2氷0-6 m、折射率为1.5 的薄玻璃片上，试问从玻璃片反射的光中哪些波长的光最强？2-7.题图绘出了测量铝箔厚度D的干涉装置结构。

两块薄玻璃板尺寸为75mm x 25mm。

在钠黄光（=0.5893 m ）照明下，从劈尖开始数出60个条纹（准确地说是从劈尖开始数出61个明条纹或暗条纹），相应的距离是30 mm，试求铝箔的厚度 D = ?若改用绿光照明，从劈尖开始数出46.6 mm，试求这绿光的波长。

2-8.如图所示的尖劈形薄膜，右端厚度h为0.005cm,折射率n = 1.5，波长为0.707 m的光以30°角入射到上表2-8题用图习题2-1.如图所示，两相干平行光夹角为第二章，在垂直于角平分线的方位上放置一观察屏,2-2题用图2-1题用图试证明屏上的干涉亮条纹间的宽度为:2-7题用图100个条纹，其间距离为ZJflWH -----面，求在这个面上产生的条纹数。

若以两块玻璃片形成的 空气尖劈代替，产生多少条条纹？2-9.利用牛顿环干涉条纹可以测定凹曲面的曲率半 径，结构如图所示。