应用光学2018(第二章)2

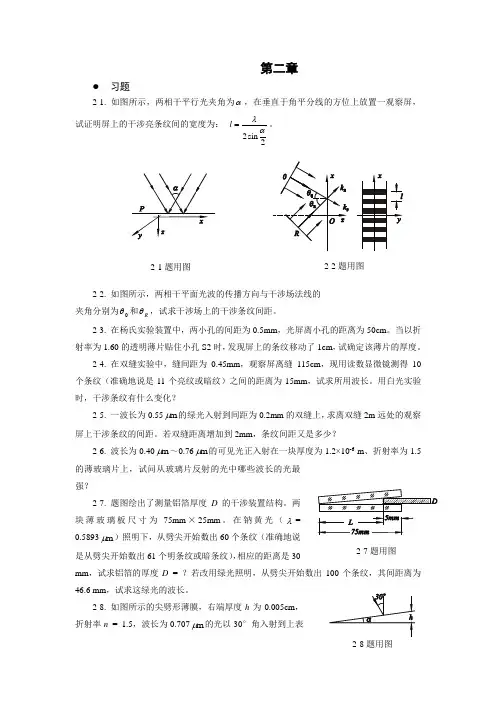
第二章习题2-1. 如图所示，两相干平行光夹角为α，在垂直于角平分线的方位上放置一观察屏，试证明屏上的干涉亮条纹间的宽度为： 2sin2αλ=l 。

2-2. 如图所示，两相干平面光波的传播方向与干涉场法线的 夹角分别为0θ和R θ，试求干涉场上的干涉条纹间距。

2-3. 在杨氏实验装置中，两小孔的间距为0.5mm ，光屏离小孔的距离为50cm 。

当以折射率为1.60的透明薄片贴住小孔S2时，发现屏上的条纹移动了1cm ，试确定该薄片的厚度。

2-4. 在双缝实验中，缝间距为0.45mm ，观察屏离缝115cm ，现用读数显微镜测得10个条纹（准确地说是11个亮纹或暗纹）之间的距离为15mm ，试求所用波长。

用白光实验时，干涉条纹有什么变化？2-5. 一波长为0.55m μ的绿光入射到间距为0.2mm 的双缝上，求离双缝2m 远处的观察屏上干涉条纹的间距。

若双缝距离增加到2mm ，条纹间距又是多少？2-6. 波长为0.40m μ～0.76m μ的可见光正入射在一块厚度为1.2×10-6 m 、折射率为1.5的薄玻璃片上，试问从玻璃片反射的光中哪些波长的光最强？2-7. 题图绘出了测量铝箔厚度D 的干涉装置结构。

两块薄玻璃板尺寸为75mm ×25mm 。

在钠黄光（λ=0.5893m μ）照明下，从劈尖开始数出60个条纹（准确地说是从劈尖开始数出61个明条纹或暗条纹），相应的距离是30mm ，试求铝箔的厚度D = ？若改用绿光照明，从劈尖开始数出100个条纹，其间距离为46.6 mm ，试求这绿光的波长。

2-8. 如图所示的尖劈形薄膜，右端厚度h 为0.005cm ，折射率n = 1.5，波长为0.707m μ的光以30°角入射到上表2-1题用图2-2题用图2-7题用图2-8题用图面，求在这个面上产生的条纹数。

若以两块玻璃片形成的空气尖劈代替，产生多少条条纹？2-9. 利用牛顿环干涉条纹可以测定凹曲面的曲率半径，结构如图所示。

第二章共轴球面系统的物像关系本章内容：共轴球面系统求像。

由物的位置和大小求像的位置和大小。

φ U ˊ - UO C A A ˊ n n ˊ P- LrL’II’Q1. 符号规则反射情形看成是折射的一种特殊情形：n’= －n把反射看成是n’= －n 时的折射。

往后推导公式时，只讲折射的公式；对于反射情形，只需将n’用－n代入即可，无需另行推导。

（1） 物像位置关系式rn n l n l n -=-'''2. 近轴光学的基本公式（2） 物像大小关系式这就是物像大小的关系式。

利用公式就可以由任意位置和大小的物体，求得单个折射球面所成的近轴像的大小和位置。

对由若干个透镜组成的共轴球面系统，逐面应用公式就可以求得任意共轴系统所成的近轴像的位置和大小。

l n nl y y '''==β3. 共轴理想光学系统的基点——主平面和焦点近轴光学基本公式的缺点：物面位置改变时，需重新计算，若要求知道整个空间的物像对应关系，势必要计算许多不同的物平面。

已知两对共轭面的位置和放大率，或者一对共轭面的位置和放大率，以及轴上的两对共轭点的位置，则其任意物点的像点就可以根据这些已知的共轭面和共轭点来求得。

光学系统的成像性质可用这些基面和基点求得最常用的是一对共轭面和轴上的两对共轭点。

（1） 放大率β=1的一对共轭面——主平面rn n l n l n -=-'''l n nl y y '''==β不同位置的共轭面对应着不同的放大率。

放大率β=1的一对共轭面称为主平面。

物平面称为物方主平面，像平面称为像方主平面。

两主平面和光轴的交点分别称为物方主点和像方主点，用H 、H’表示，H 和H’显然也是一对共轭点。

主平面性质：任意一条入射光线与物方主平面的交点高度和出射光线与像方主平面的交点高度相同（2）无限远轴上物点和它所对应的像点F’——像方焦点rn n l n l n -=-''' 当轴上物点位于无限远时，它的像点位于F’处。

第二章 例 题例题2.1 凸平透镜r 1=100mm ，r 2=∞，d=300mm ，n=1.5，当物体在-∞时候，1）求高斯像面的位置；2）在平面上刻十字，问其共轭像在什么位置；3）当入射高度为h=10mm ，问光线的像方截距是多少？和高斯像面相比相差多少？说明什么问题？解：1）根据近轴光线光路计算公式可以求出高斯像面的位置。

将1111,' 1.5,1,100l n n r mm =-∞===代入单个折射球面成像公式'''n n n n l l r--=，可以求得1'300l mm =。

又由题意d=300mm ，发现此时所成的像在凸平透镜的第二面上。

2）由光路可逆原理知道，若在平面上刻十字，其共轭像应在物方 -∞处。

3）当入射高度为h=10mm 时，光路如下图所示：此时利用物在无限远时，L =−∞时， 公式sin sin 'sin '''sin ''(1)sin 'h I r n I I n U U I I I L r U ⎧=⎪⎪⎪=⎪⎨⎪=+-⎪⎪=+⎪⎩中的第一和第四式求解得： ※ 光线经过第一面折射时，11110sin 0.1100h I r ===，所以1 5.739o I =。

又11111sin 'sin 0.10.06667' 1.5n I I n ==⨯=，所以1'arcsin 0.06667 3.822o I ==，1111''(0 5.739 3.822) 1.9172o o U U I I =+-=+-=，1111sin '0.0667'11001299.374sin '0.0334547I L r mm U ⎛⎫⎛⎫=⨯+=⨯+= ⎪ ⎪⎝⎭⎝⎭。

※ 光线再经过第二个面折射，21'0.626L L d mm =-=-，21' 1.9172o I U -==，则2222sin 'sin 1.5sin1.91720.05018'o n I I n ==-=-，2' 2.87647o I =-。

应用光学试题第二章一、填空题（建议每空1分）（请同学们不要写错别字，数字不要用大写，术语要标准，否则按错处理，不要用科学记数法如4101⨯）I 级I 级1空1、 焦点又称为后焦点或第二焦点。

像方2、过像方焦点'F 作一垂直于光轴的平面即为 焦平面。

像方3、像方焦点'F 是像方焦平面上的一个特殊点，该点对应的是物方孔径角=u 度的一束平行于光轴的平行光。

4、从物方焦点F 发出的光经过系统后均为平行于 的光。

光轴5、过 作垂直于光轴的平面称为物方焦平面。

物方焦点6、垂轴放大率为=β 倍的这对共轭平面为主平面（简称主面）。

17、主平面与光轴的交点称为 。

主点8、像方主平面与 的交点称为像方主点'H 。

光轴9、焦距属于沿轴线段，以各自的 为原点判断其符号。

主点10、 焦距可表示式为tguh 。

物方11、光学系统的 可以看作是焦距的另外一种表示形式， 光焦度12、 是指角放大率1+=γ的一对共轭点。

节点13、经过物方节点的光线其共轭光线经过 节点。

像方14、 法主要是应用光学系统基点和基面的性质，通过选用适当的光线或辅助线画出其共轭光线的方法。

图解15、牛顿公式是以各自的为原点确定物、像的具体位置。

焦点16、高斯公式是以为原点来描述物、像的具体位置。

主点17、将一个正单透镜与一个负单透镜进行胶合，称之为透镜。

双胶合18、望远系统是最典型的光学系统，其系统焦点位于无穷远处，焦距为无限大。

无焦19、望远系统的光学间隔=∆。

20、是由两个折射面包围的一种透明介质构成的光学元件，折射面可以是球面、平面或非球面。

透镜21、是指当透镜的厚度与焦距或曲率半径相比是一个很小的数值时，厚度d可忽略不计的透镜。

薄透镜22、透镜主平面与之间的距离为焦距。

焦点23、透镜物与像之间的距离称为。

共轭距24、筒长L是指第一个光组到之间的距离。

像面（或像平面）25、是指系统最后一面到像平面之间的距离。

后工作距离26、按照透镜形状的不同，正透镜又可分为透镜、平凸透镜及月凸透镜，双凸27、负透镜又分为透镜、平凹透镜及月凹透镜，其特征是中心厚度比边缘厚度薄。