第九讲 丰富的图形世界二
- 格式:pdf
- 大小:414.70 KB
- 文档页数:7

七年级数学丰富的图形世界(二)某某教育版【本讲教育信息】一. 教学内容:丰富的图形世界(二)1. 三视图及简单几何体三视图的画法;2. 生活中常见平面图形——多边形、扇形。
二. 知识要点:1、三视图的定义:主视图:从正面看到的图叫做主视图;俯视图:从上面看到的图叫做俯视图;左视图:从左面看到的图叫做左视图。
主视图、俯视图、左视图统称为三视图。
2、三视图画法规则:(1)左视图在主视图右侧,俯视图在主视图下方;(2)主视图左视图同高,主视图俯视图同宽;(3)已知由相同立方体组合而成的几何体的俯视图画主视图及左视图时,遵循“画主看俯列,画左看俯行,取大左右画”的规则。
3、多边形、扇形定义:多边形定义:一些不在同一直线上的线段依次首尾相连组成的封闭平面图形;扇形定义:由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形。
4、多边形分割规律:若多边形的边数为n,从一个顶点出发可连接出(n-3)条对角线,这(n-3)条对角线将n边形分割成(n-2)个三角形。
三. 重点、难点、考点:重点:三视图定义、画法,多边形分割成三角形的规律;难点:简单几何体三视图的画法;考点:画出简单几何体的三视图是中考命题的热点内容。
折、剪平面图形(或纸片)以及探索图形中蕴含的规律,在中考中的比重呈上升趋势。
一般以填空题、选择题的形式出现,属于中低档题。
【典型例题】例1.小明从正面观察图1所示的两个物体,看到的是()图1图2答案:C指导:本例属于已知实物确定三视图的题型。
正面观察的图像即为主视图,本题考查的是学生基本的抽象概括能力,较为简易。
例2. 将图3所示的一个直角三角形ABC(∠C=90°)绕斜边AB旋转一周,所得到的几何体的主视图是下面四个图形中的_____________(只填序号)图3图4答案:B指导:画物体的三视图应注意三视图的特征:主视图体现物体正面看时的高和宽,俯视图体现物体上面看时的长和宽,左视图体现物体左面看时的高和宽,画三视图基本规则是“主左同高,主俯同宽”。


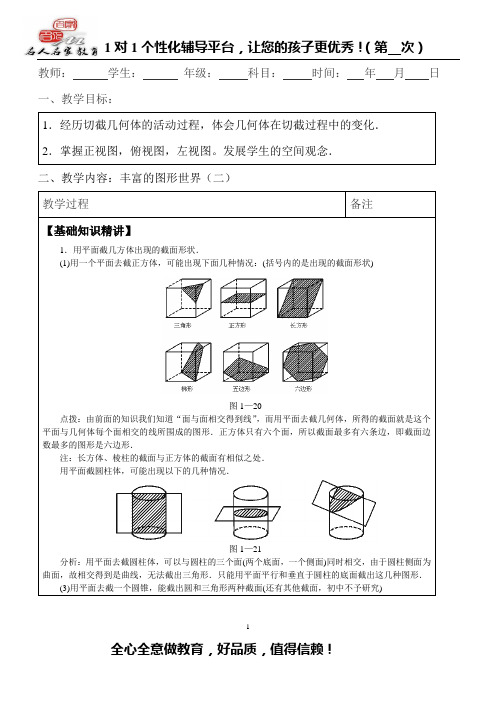
丰富的图形世界(二)一、重点知识归纳及讲解1、用平面截几何体所得截面的形状用一个平面从不同的方向去截同一个几何体,所得到的截面形状可能是不同的.在用一个平面去截几何体时,注意观察几何体在切截过程中的变化,充分想像截面可能的形状,可以先找出平面和几何体的面相交而成的线,然后再判断这些线围成的截面形状.2、从不同方向观察物体从不同方向观察同一物体时,可能看到不一样的结果.当观察画在纸上面的立体图形时,只能通过想像,推出从其他方向观察这个物体所可能得到的结果.3、物体的主视图、左视图、俯视图从不同的方向观察同一物体时,可能看到不同的图形,其中,把正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图,合称三视图.这里所说的主视图、俯视图、左视图是相对于观察者而言的,位于物体不同方向的观察者,他们所画出的主视图、俯视图、左视图可能是不同的.4、多边形多边形是由一些线段首尾顺次相连围成的封闭图形,多边形根据它的边数可以分为三角形(即三边形)、四边形、五边形等,多边形的边数为n(n≥3)的叫做n边形.在多边形中,三角形是最基本的图形.从一个多边形的某个顶点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成若干个三角形,n边形可以分割成(n-2)个三角形,这样,多边形可以化归为三角形来研究.5、圆、弧及扇形一条线段绕着它的一端旋转一周形成的图形叫做圆.圆上两点之间的部分叫做弧,弧是一条曲线.由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形,扇形是由一条曲线和两条线段组成的封闭图形.一个圆可以被它的半径分割成若干个扇形.二、难点知识剖析1、物体三视图的画法及识别对于简单物体的三视图,要能识别观察方向,能够想像出物体的原形.对于简单物体以及立方体的简单组合,画它的三视图的关键是确定它们有几列,以及每列方块的个数.由俯视图画主视图和左视图的方法有二:一是先摆出几何体,再画出主视图和左视图;二是先由俯视图确定主视图,左视图的列及每列方块的个数,主视图与俯视图列数相同,其每列方块数是俯视图该列中最大数字,左视图的列数与俯视图的行数相同,其每列的方块数是俯视图该行中的最大数字.2、平面图形的组合和分割再复杂的平面图形都是由若干简单的基本图形组合而成的,生活中许多美丽的图案,就是由三角形、正方形、长方形、多边形、圆、扇形等基本图形组成.对于平面图形能进行简单的分割和组合.三、典型例题解析例1、一正方体截去一角后,剩下的几何体有多少条棱?多少个面?多少个顶点?分析:因为截去一角有多种截法,所以应分情况讨论.图(2)解:(1)如图(1),剩下的几何体有15条棱,7个面,10个顶点.(2)如图(2),剩下的几何体有14条棱,7个面,9个顶点.(3)如图(3),剩下的几何体有13条棱,7个面,8个顶点.(4)如图(4),剩下的几何体有12条棱,7个面,7个顶点.例2、一几何体被一平面所截后,得一圆形截面,则原几何体是什么形状?分析:要使截面是一个圆形,则必须使原几何体有一个曲面,这样的几何体可能是圆锥、圆柱、圆台.解:如图所示,原几何体可能是:(1)圆锥;(2)圆柱;(3)圆台.例3、分别画出如图所示由五块方块摆成两种不同形状的三视图.分析:在画三视图前,要仔细观察物体形状,充分发挥空间想像能力,分析它的三视图的可能形状.解:(1)的三视图如图(1)所示.(2)的三视图如图(2)所示.例4、如图所示是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图、左视图.分析:从正面看,它有三列,每列的方块数依次是2、3、2;从左面看,它有两列,每列的方块数分别是3、2.解:这个几何体的主视图、左视图如图所示.例5、从一个七边形的某个顶点出发,分别连结这个点和其余各顶点,可以把这个七边形分割成多少个三角形?先想一想,再画一画.分析:按这种方式分割,四边形可分成两个三角形;五边形可分成三个三角形;六边形可分成四个三角形;七边形可分成五个三角形,一般地,n边形可分成(n -2)个三角形.解:七边形可被分割成五个三角形,如图所示.例6、在一个圆中任意画4条半径,可以把这个圆分成几个扇形?分析:图中一目了然的有4个扇形,此外,由相邻两个扇形组成的扇形有4个,由相邻三个扇形组成的扇形还有4个,因而一共有12个扇形,解此道题时一定要注意图形的组合.解:如图所示,4条半径可以把这个圆分成12个扇形.。


《丰富的图形世界》(第2课时)教案2doc初中数学教学目标:通过七巧板体会数学的乐趣教学重点:用七巧板拼出各种图案教学难点:用七巧板制造出新的图案教学内容:七巧板介绍:七巧板也称〝七巧图〞,是中国闻名的拼图玩具。
因设计科学,构思巧妙,变化无穷,能活跃形象思维,专门是启发儿童聪慧,因此深受欢迎。
传到国外后,风行世界,号称〝唐图〞,意即〝中国的图板〞。
讲起〝唐图〞,自然与唐代有关,它的发明是受了唐代〝燕几〞的启发。
〝燕〞通〝宴〞,所谓〝燕几〞,确实是唐朝人创制的专用于宴请来宾的几案,其特点是能够随来宾人数多少而任意分合。
它的大致形制,传世的«韩熙载夜宴图»中可见一斑。
到了北宋,任官秘书郎的黄伯思对这种〝燕几〞作进一步改进,设计成六件一套的长方形案几系列,既可视来宾多少拼合,又可分开摆设古玩书籍。
案几有大有小,但都以六为度,因取名〝骰子桌〞。
他的朋友宣谷卿看见这套〝骰子桌〞后,十分观赏,再为他增设一件小几,以便增加变化,因此又改名〝七星桌〞。
此后,黄伯思专门编了一部«燕几图»公布自己的发明,除介绍〝七星桌〞的尺寸外,还依其组合变化将图形分为种,各取名义如〝三函〞、〝屏山〞、〝回文〞、〝垂箔〞等等。
七巧板的雏型,就在这兼备有用价值和艺术审美的图形拼合中产生了。
元明两代,中国的组合式家具顺应都市生活的需要,有了长足进展。
许多能工巧匠都借鉴黄伯思的«燕几图»,运用平面木块进行〝纸上谈兵〞式的设计。
有个叫严澄的明朝官员依照«燕几图»的原理,大胆引进三角形,设计成一套十三件的几案系列,合起来呈蝶翅形,分开组合的图形可达百余种,并据此编成«蝶几谱»。
在此基础上,从工师设计图板中脱颖而出的拼图玩具产生了,其时刻大致在明末清初,因为是用薄木片或厚纸板做成七件套组合,俗成〝七巧牌〞,溯其渊源,同黄伯思的〝七星〞不无联系。