当前位置：文档之家 › 圆周角和圆心角的关系(2)PPT课件

圆周角和圆心角的关系(2)PPT课件

  • 格式：pptx
  • 大小：429.56 KB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

九年级数学上册第28章圆：圆心角和圆周角第2课时ppt课件新版冀教版

九年级数学上册第28章圆：圆心角和圆周角第2课时ppt课件新版冀教版
∴ ∠ABC = ∠AOC. 你能写出这个命题吗?
B
圆上一条弧O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆 心角∠AOC的大小关系会怎样?
提示:能否也转化为1的情况? 过点B作直径BD.由1可得: ∠ABD = ∠AOD,∠CBD = ∠COD,
. O
B
C
1.首先考虑一种特殊情况：当圆心(O)在圆周角(∠ABC)的 一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
解:∵∠AOC是△ABO的外角， ∴∠AOC=∠B+∠A.
A C
∵OA=OB，
●O
∴∠A=∠B.
B
∴∠AOC=2∠B.
即∠ABC = ∠AOC. 你能写出这个命题吗?
圆周角的定义及性质
圆心角顶点发生变化时,我们得到几种情况?
.A
A.
..A
O
.
.
O
O
B
C
B
C
B
C
思考：三个图中的∠BAC的顶点A各在圆的什么位置？ 角 的两边和圆是什么关系？
你能仿照圆心角的定义给圆周角下定义吗?
圆周角定义: 顶点在圆上,两边都与
圆相交的角叫圆周角.
A
特征： ①角的顶点在圆上. ②角的两边都与圆相交.
一条弧所对的圆周角等于它所对的圆心角的一半.
如果圆心不在圆周角的一边上,结果会怎样? 2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆 心角∠AOC的大小关系会怎样?
提示:能否转化为1的情况?
过点B作直径BD.由1可得: ∠ABD = ∠AOD,
AD C
●O
∠CBD = ∠COD,
B ∴∠ABC = ∠AOC.

北师大版九年级数学下册.2：圆周角和圆心角的关系2课件

北师大版九年级数学下册.2：圆周角和圆心角的关系2课件

解∵AB为直径 ∴∠BCA=90° 在Rt△ABC中， ∠ABC=30°，AB=10cm
∴
B O
C
A
议一议
如图，A，B，C，D是⊙O上的四点，AC为⊙O的直径， 请问∠BAD与∠BCD之间有什么关系？为什么？
D
A
解：∠BAD与∠BCD互补
∵AC为直径
∴∠ABC=90°,∠ABC=90°
O
∵∠ABC+∠BCD+∠ABC+∠BAD=360°
视察图，圆周角∠BAC=90°，弦BC是直径吗？为什
么？
A
解：弦BC是直径。
连接OC、OB
∵∠BAC=90° ∴∠BOC=2∠BAC=180°
B
O
C
（圆周角的度数等于它所对弧上的
圆心角的度数的一半）
∴B、O、C三点在同一直线上
∴BC是⊙O的一条直径
直径所对的圆周角是直角； 90°的圆周角所对的弦是直径。在书上画记，背读
3.4 圆周角和圆心角的关系 第二课时
课前复习
1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角. 2.圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
3.圆周角定理推论: 同弧 (等弧)所对的圆周角相等.
4.在同圆或等圆中,
Dபைடு நூலகம்
B E
●O
相等的圆周角所对的弧相等. 5.在同圆或等圆中,
4.如图，⊙O1 与⊙O2 都经过 A，B 两点，且点 O2 在⊙O1 ︵
上，点 C 是 AO2 B 上的一点（点 C 不与 A，B 重合），AC 的延长线交⊙O2 于点 P，连接 AB，BC，BP。 （1）根据题意将图形补充完整；
︵ （2）当点 C 在 AO2 B 上运动时，图中大小不变的角有哪

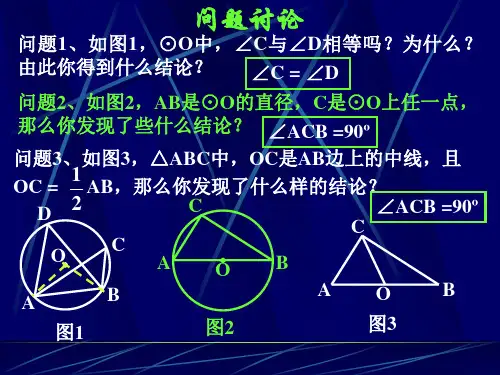
课件233圆周角和圆心角的关系.ppt

课件233圆周角和圆心角的关系.ppt

径。求证：AB ·AC = AE ·AD
分析：要证AB ·AC = AE ·AD
A
AC AD AE AB
O
△ADC∽ △ABE B
DC
或△ACE∽ △ADB E
题后思：1、证明题的思路寻找方法； 2、等积式的证明方法； 3、辅助线的思考方法。
讨论与思考 C
如图，CD是⊙O的直径，
弦AB⊥CD于E，那么你
问题讨论
问题1、如图1，⊙O中，∠C与∠D相等吗？为什么？ 由此你得到什么结论？ ∠C = ∠D
问题2、如图2，AB是⊙O的直径，C是⊙O上任一点， 那么你发现了些什么结论？ ∠ACB =90º
问题3、如图3，△ABC中，OC是AB边上的中线，且
OC = 1 AB，那么你发现了什么样的结论？
D2
C
∠ACB =90º C
O
能得到什么结论？
结论：Βιβλιοθήκη AEB（1）AE = BE，AC = BC，AD = BD D
（2）AC = BC，∠CAB = ∠ABC = ∠D，
∠ACE =∠BCE =∠DAB
（3）BC2 = AC2 = CE ·CD，AD2 = DE ·DC
BE2 = AE2 = DE ·CE
小结与作业
1、本节课我们学习了哪些知识？ 2、圆周角定理及其推论的用途你都知道了吗？ 3、证明题思路的寻找方法如何？ 4、证明等积式的一般思路你掌握了吗？
O
C A
O
B
A
B
AO
B
图1
图2
图3
自学与思考
1、圆周角定理的推论1、2、3的内容分别是什么？ 你是怎样理解这些推论的？
2、从课本例2的学习中你认为证明等积式的一般思 路是怎样的？

北师版初中数学九年级下册精品教学课件 第三章圆 4 圆周角和圆心角的关系 第2课时

北师版初中数学九年级下册精品教学课件 第三章圆 4 圆周角和圆心角的关系 第2课时
∴△ABC是直角三角形,∠B=90°,∴AC是直径,∴∠D=90°.
在 Rt△ACD 中,由勾股定理,得 AD= 2 - 2 =
102 -42 =2 21.
返回首页
4.如图,AB是☉O的直径,CD是☉O的弦,连接AC,AD.若∠CAB=35°,则
∠ADC的度数为 55° .
如图,连接BD.
又∠BPC+∠BAC=180°,∴∠BPC=120°.
(2)证明 如图,在PA上截取PD=PC,连接CD.
∵AB=AC=BC,∴∠APB=∠APC=60°,
∴△PCD为等边三角形,∴∠ADC=120°.
∵∠BPC=120°,∴∠BPC=∠ADC.
又∠PBC=∠PAC,∴△ACD≌△BCP,
∴AD=BP,∴PA=PB+PC.
∵AB是☉O的直径,
∴∠ADB=90°.
∵∠CAB=35°,∠CAB=∠CDB,
∴∠CDB=35°.
∴∠ADC=55°.
返回首页
5.如图,已知 = = ,P 为 上一点.

(1)求∠BPC的度数;
(2)求证:PA=PB+PC.
返回首页
(1)解 ∵ = = ,
∴AB=BC=AC,∴∠BAC=60°.
B.121°
C.118°
D.112°
∵四边形ABCD为☉O的内接四边形,
∴∠A=180°-∠BCD=180°- 121°=59°,
∴∠BOD=2∠A=2×59°=118°.
返回首页
3.如图,点A,B,C,D在圆上,AB=8,BC=6,AC=10,CD=4,则AD= 2 21 .
∵62+82=102,即AB2+BC2=AC2,

《圆周角和圆心角的关系》第二课时

《圆周角和圆心角的关系》第二课时

1.为什么有些电影院的坐位排列（横排）呈圆弧形？说一说这 种设计的合理性。 答：有些电影院的坐位排列呈圆弧形，这样设计的理由是尽 量保证同排的观众视角相等。 2.如图，哪个角与∠BAC相等？ A
答：∠BDC= ∠BAC 。
D
B C
• 1.判断题： • （1）同圆或等圆中，等弧所对的圆周角相等.（ √） • （2）90°的角所对的弦是直径. （X ） • （3）同弦所对的圆周角相等. （X ）
（1）当船与两个灯塔的夹角 ∠α大于“危险角”时，船位于 哪个区域？为什么？
解：（1）当船与两个灯塔的夹角∠α大于“危险角” ∠C时， 船位于暗礁区域内（即⊙O内）。理由是： 连接BE. 假设船在⊙ O 上，则有∠ α=∠C ，这与∠ α ＞∠ C 矛盾，所以 船不可能在⊙O上；假设船在⊙O外，则有∠ α＜∠AEB，即 ∠α＜∠C，这与∠α＞∠C矛盾，所以船不可能在⊙O外。因 此，船只能位于⊙O内。
（2）当船与两个灯塔的夹角 ∠α小于“危险角”时，船位于 哪 个区域？为什么？ 解：（ 2 ）当船与两个灯塔的 夹角∠α小于“危险角” ∠C 时， 船 位 于 暗 礁 区 域外 （即 ⊙O外）。理由是：
假设船在⊙O上，则有∠α=∠C，这与∠α＜∠C矛盾，所以 船不可能在⊙O上；假设船在⊙O内，则有∠α＞∠AEB，即 ∠α＞∠C，这与∠α＜∠C矛盾，所以船不可能在⊙O内。 因此，船只能位于⊙O外。
A
O1
O
B
4
cm
2.如图,△ABC的顶点均在⊙O上,AB=4, ∠C=30°, 求⊙O的直径. 解:过B作直径BF交⊙O于点F, A 连接AF B ∵BF是⊙O的直径 ∴∠BAF=90° O 在Rt△ABF中，∠F=30° C ∴BF=2AB 又∵AB=4 F E ∴BF=8 即⊙O直径为8

人教版九年级数学上册课件：第24章圆24.1.4 圆周角和圆心角、弧的关系(共20张PPT)

人教版九年级数学上册课件：第24章圆24.1.4 圆周角和圆心角、弧的关系(共20张PPT)
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/9/42021/9/42021/9/42021/9/49/4/2021 •14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年9月4日星期六2021/9/42021/9/42021/9/4 •15、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2021年9月2021/9/42021/9/42021/9/49/4/2021 •16、教学的目的是培养学生自己学习，自己研究，用自己的头脑来想，用自己的眼睛看，用自己的手来做这种精神。2021/9/42021/9/4September 4, 2021 •17、儿童是中心，教育的措施便围绕他们而组织起来。2021/9/42021/9/42021/9/42021/9/4
我们来分析第（1）种情况，如图（1），圆心 O在∠BAC的一条边上.
知2－讲
O A B O O C C A A C C A 1 2 B O C .
对于第（2）（3）种情况，可以通过添加辅助线（图 （2）（3）），将它们转化为第（1）种情况.从而得 到相同的结论（请你自己完成证明）.
• You have to believe in yourself. That's the secret of success. 人必须相信自己，这是成功的秘诀。
•
知1－练
1 (中考·柳州)下列四个图中，∠x为圆周角的是( C)
（来自《典中点》）
知1－练
2 如图所示，图中的圆周角共有___4___个，其中A⌒B 所对的圆周角是_∠__C__与_∠__D_____，C⌒D所对的圆周角 是_∠__A_与__∠__B___．

圆心角-课件ppt


O
C B
8.如图,圆O中,AB是直径,半径CO⊥AB,
D是CO的中点,DE∥AB,求∠ABE的度数.
C
E
D
A O
B
圆内接四边形：
（顶点都在圆上的四边形叫圆内接四边形）
1.如图,在⊙O中,∠BAD=50°,求∠C的大小.
2.若∠BAD=80°,求∠C的大小.
A
3.若∠BCD=120°,求∠A的大小.
思考：如何证明？
已知EA=3,EB=6,EC=8,则ED=___
船在航行过程中,船长常常通过测定角度来确定
是否会遇到暗礁,如图,A,B表示灯塔,暗礁分布在经过
A,B两点的一个圆形区域内,C表示一个危险临界点,
∠ACB就是”危险角”,当船与两个灯塔的夹角大于”
危险角”时,就有可能触礁.
(1)当船与两个灯塔的夹角∠a 等于“危险角”时,船位于哪 个区域?为什么?
C
C
●O
B
●O
B
圆周角定理：
一条弧所对的圆周角等于它所对的圆心角的一半
.
即：∠ABC = 1 ∠AOC
2
四、巩固训练：
1.如图,在⊙O中,∠BOC=50°,求∠A的大
小.
解: ∠A= 1∠BOC=25°.
2
B C
●O A
2.练习:在下列各图中， ∠α１＝ 150°，∠α２＝ 60°，
C
７５º α１
A D
E
.O
C
B
5.(1)如图,在⊙O中,弦AB、CD相交于点E，则△ACE 与△ DBE有什么关系？并说明理由。
A D
E
.O
C
B
5.(2) 线段EA、EB、EC、ED有什么关系？并说明理 由。

圆周角和圆心角的关系PPT课件(北师大版)

3．如图，经过原点O的⊙P与x，y轴分别交于A，B两点，点C是劣弧OB 上一点，则∠ACB的度数是( C ) A．80° B．100° C．90° D．无法确定
4．如图，△ABC为⊙O的内接三角形，AB为⊙O的直径，点D在⊙O上， ∠ADC＝54°，则∠BAC的度数等于_______36°
5．如图，△ABC的三个顶点在⊙O上，CD是直径，∠B＝40°，则 ∠ACD的度数是_5_0_°_．
6．(202X·温州模拟)如图，AB为⊙O的直径，点C在⊙O上，延长BC至 点D，使DC＝CB.延长DA与⊙O的另一个交点为E，连接AC，CE. (1)求证：∠B＝∠D； (2)若AB＝4，BC－AC＝2，求CE的长．
解：(1)∵AB 是⊙O 的直径，∴∠ACB＝90°，∴AC⊥BC.∵CD＝CB， ∴AD＝AB，∴∠B＝∠D (2)设 BC＝x，则 AC＝x－2.在 Rt△ABC 中， AC2＋BC2＝AB2，∴(x－2)2＋x2＝42，解得 x1＝1＋ 7，x2＝1－ 7(舍 去)．∵∠B＝∠E，∴∠D＝∠E，∴CD＝CE.∵CD＝CB，∴CE＝CB ＝1＋ 7
︵︵ 9．如图，已知∠EAD 是圆内接四边形 ABCD 的一个外角，并且BD＝DC. 求证：AD 平分∠EAC.
解：∵四边形 ABCD 是圆内接四边形，∴∠EAD＝∠DCB.又∵B︵D＝D︵C， ∴∠DAC＝∠DCB.∴∠EAD＝∠DAC，∴AD 平分∠EAC
10．(202X·安徽模拟)如图，点P是等边三角形ABC外接圆⊙O上的 点．在下列判断中，不正确的是( C ) A．当弦PB最长时，△APC是等腰三角形 B．当△APC是等腰三角形时，PO⊥AC C．当PO⊥AC时，∠ACP＝30° D．当∠ACP＝30°时，△BPC是直角三角形
第三章 圆

圆周角和圆心角的关系ppt课件

50°，则∠EBC+∠ADC 的度数为 _______.
-18-
3.4 圆周角和圆心角的关系
解析：如解析图，连接 AB，DE，则∠ABE=∠ADE. ∵ 所对的圆心角的度数为 50°，∴∠ABE= ∠ADE =25°. ∵ 点 A，B，C，D 在 ⊙O 上 ，∴四边形 ABCD 是圆内接四边形， ∴∠ABC+∠ADC=180°， ∴∠ABE+∠EBC+∠ADC=180°， ∴∠EBC+∠ADC=180°-∠ABE=180°-25°=155°． 答案：155° 题型解法：本题考查了圆周角定理和圆内接四边形的 性质，作出辅助线构建圆内接四边形是解题的关键．
-10-
3.4 圆周角和圆心角的关系
■考点四 圆内接四边形
定义
四边形的四个顶点都在同一个圆上，这个四边形叫做圆内接四边形，这个 圆叫做四边形的外接圆
推论 圆内接四边形的对角互补
拓展 圆内接四边形的任何外角等于内对角
注意 并不是所有的四边形都存在外接圆，只有对角互补的四边形才存在外接圆
-11-
3.4 圆周角和圆心角的关系
A． 20° B． 40°
C． 50° D． 70°
-7-
3.4 圆周角和圆心角的关系
3. 如图，已知△ABC 的三个顶点都在同一圆上，且 AC=6，BC=8，AB=10， 则该圆的半径长是 ________.
（第 3 题图）
（第 4 题图）
4. 如图，AB=BC，∠ABC =120°，AD 为 ⊙O 的直径 ，AD=6，那么 AB 的
值为 ______.
-8-
3.4 圆周角和圆心角的关系
5. 如图，AB=AC，AB 是直径，求证：BC=2DE． （第 5 题图）

圆周角和圆心角的关系精品PPT课件


演讲人：XXXXXX
时 间：XX年XX月XX日
2、练习
①②
顶两
点边
A
在分
圆别
上与
圆
还
有
另
一
个
交
点
A
二、认识圆周角
A
P
B
P
B
O
O
P O
B
P
O
A
B
P O
A
B
三、探究圆周角与圆心角的关系
环节一：作图
.A B.
●O
我们今天就研究一条弧所对 圆周角与圆心角的大小关系
一条弧对1个圆心角，对无数个圆周角 从圆心与圆周角的位置关系来看，我们可以将这无数个圆心角分成三类：圆 心在圆周角的边上，圆心在圆周角的内部，圆心在圆周角的外部。
∠ABC=
1 2
∠AOC
三、探究圆周角与圆心角的关系 环节四：得出结论 圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的_一__半__。
推论
同弧或等弧所对的圆周角______相__等。
三、探究圆周角与圆心角的关系
环节五：针对练习
1、如图，在⊙O中，∠BOC=50°，则∠BAC=
。
2、如图，点A，B，C是⊙O上的三点，∠BAC=40°，则∠BOC=
所用知识：①外角等于不相邻的 两个内角之和；②圆的半径相等
三、探究圆周角与圆心角的关系
环节三：推理证明
AD C
O
连接BO并延长作直径，将问题
转化为第一种情况解答，转化
B
是一种很重要的数学方法
∠B=
1 2
∠AOC
三、探究圆周角与圆心角的关系 环节三：推理证明
A C
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

O
A O B １２０º
A
B
∠α３＝ 120°，∠α４＝ 140° .
C
D
３０º O
α３
O
α４
A B
A １１０º
B
C
3.求圆中角X的度数
D
120°
.O C
C
O.
O
70° x
A
B
X A
A
B
B
C
4.如图，圆心角∠AOB=100°，则∠ACB=__1_3_0_°__。
5、 如图，在直径为AB的半圆中，O为圆心， C、D为半圆上的两点，∠COD=500，则 ∠CAD=_________
画几个？试画出。 答：无数个 3.这些圆周角有什么关系？为什么？答：相等
圆周角定理推论:
D A
C 1. 同弧 (等弧) 所对的圆周角相等.
都等于这条弧所对的圆心角的一半.
O
思考: 在同圆或等圆中
相等的圆周角所对的弧相 B 等吗?
2. 在同圆或等圆中,
相等的圆周角所对的弧相等.
推论中， ⑴“同弧或等弧”能否改为“同弦或等弦”？为什 么？
A D
E
.O
C、CD相交于点E，则△ACE 与△ DBE有什么关系？并说明理由。
A D
E
.O
C
B
5.(2) 线段EA、EB、EC、ED有什么关系？并说明理 由。
相交弦定理 A D E .O
C
B
如图,在⊙O中,任意弦AB、CD相交于点E，则有 EA·EB=EC·ED
不能
⑵ “同圆或等圆”这一条件能否省去？
不能
1.试找出下图中所有相等的圆周角。
D
A1
87
2
3
6
45
B
C
∠1=∠4 ∠2=∠7 ∠3=∠6 ∠5=∠8
2. 在⊙o中,与∠BAC相等的角有
( ∠BDC ).
A D
A
D
(1)
.O
(2)
.O
B
C
B
C
3.如图,在⊙O中,四边形ABCD的对角线把四个内角分 成的八个角中有( 四 )对相等的角.
3练习：已知：如图， ∠APC=∠CPB=60° 求证：△ABC是等边三角形
证明： ∵∠ABC=∠APC=60°
A P
O· C
B
∠BAC=∠CPB=60° (同弧所对的圆周角相等）
∴∠ABC= ∠BAC= ∠ACB= 60°
∴△ABC等边三角形。
4、如图，△ABC的3个顶点都 在⊙O上，D是AC的中点，BD交 AC于点E，△CDE与△BDC相似 吗？为什么？
P
a
CE
(2)当船与两个灯塔的夹角∠a 小于”危险角”时,船位于哪 个区域?为什么?
(3)当船与两个灯塔的夹角∠a 大于”危险角”时,船位于哪 个区域?为什么?
O
A
B
提问与解答环节
Questions And Answers
谢谢聆听
· 学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
6、AB、AC为⊙O的两条弦，延长 CA到D，使 AD=AB，如果
∠ADB=350，求∠BOC的度数。
7.如图：OA、OB、OC都是⊙O的半径 ∠AOB=2∠BOC.则∠ACB与∠BAC大小
有什么关系？.
规律:解决圆周角和圆心角
的计算和证明问题,要准确 A
找出同弧所对的圆周角和圆 心角,然后再灵活运用圆周 角定理
B
圆周角定理推论： 圆内接四边形对角互补。
●O D
C
练习：如图,圆O中,弦AB的长等于半径， 则弦AB所对的圆心角的度数为________ 弦AB所对的圆周角的度数为________.
. O
A
B
二、探索新知
D
B E
●O
A
C
1.在圆O中，你能画出弧AC所对的圆心角吗？能画
几个？试画出。 答：一个
2.在圆O中，你能画出弧AC所对的圆周角吗？能
B
●O
B
圆周角定理：
一条弧所对的圆周角等于它所对的圆心角的一半
.
即：∠ABC = 1 ∠AOC
2
四、巩固训练：
1.如图,在⊙O中,∠BOC=50°,求∠A的大
小.
解: ∠A= 1∠BOC=25°.
2
B C
●O A
2.练习:在下列各图中， ∠α１＝ 150°，∠α２＝ 60°，
C C α２
７５º α１
思考：如何证明？
已知EA=3,EB=6,EC=8,则ED=___
船在航行过程中,船长常常通过测定角度来确定
是否会遇到暗礁,如图,A,B表示灯塔,暗礁分布在经过
A,B两点的一个圆形区域内,C表示一个危险临界点,
∠ACB就是”危险角”,当船与两个灯塔的夹角大于”
危险角”时,就有可能触礁.
(1)当船与两个灯塔的夹角∠a 等于“危险角”时,船位于哪 个区域?为什么?
九年级数学(下)
3.3 圆周角和圆心角 的关系（2）
——圆周角定理推论
一.复习 1.圆周角定义：
顶点在圆上，并且两边与圆相交的角 叫做 圆周角.
P
O
A
B
练习：
1.判别下列各图形中的角是不是圆周角，并说明理由。
不是
图１
不是
图２
是
图３
不是
图４
不是
图５
2.圆周角和圆心角的关系
A C
●O
B
A
A
C
C
●O
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
O
C B
8.如图,圆O中,AB是直径,半径CO⊥AB,
D是CO的中点,DE∥AB,求∠ABE的度数.
C
E
D
A O
B
圆内接四边形：
（顶点都在圆上的四边形叫圆内接四边形）
1.如图,在⊙O中,∠BAD=50°,求∠C的大小.
2.若∠BAD=80°,求∠C的大小.
A
3.若∠BCD=120°,求∠A的大小.